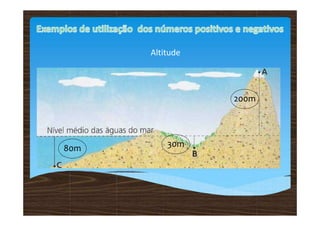
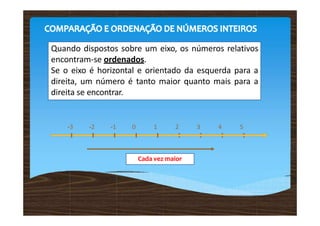
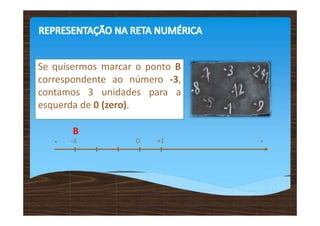
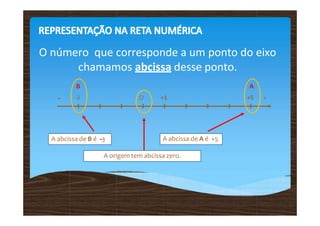
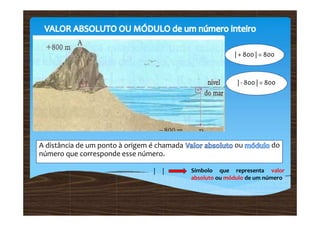
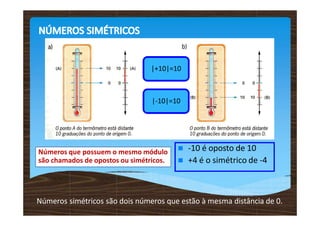
Os números inteiros relativos incluem números positivos, negativos e zero, sendo representados em uma reta numérica. A comparação entre esses números mostra que positivos são maiores que zero, zero é maior que negativos e esses aumentam da esquerda para a direita. Adições e subtrações de números relativos seguem regras específicas, onde a operação é determinada pelos sinais dos números envolvidos.

2. Os números inteiros relativos são
s
s
formados por todos os números inteiro
negativos, pelo zero e por todos o
números inteiros positivos.
Z = {..., -4, -3, -2, -1, 0, +1, +2, +3,...}
Ao conjunto dos números inteiros positivos, números inteiros negativos e
zero chamamos conjunto de números inteiros relativos.

3. e
a,
o
o
s
a
o
o
Um termómetro em certa cidade qu
marcou 10°C acima de zero durante o di
à noite e na manhã seguinte
termómetro passou a marcar 3°C abaix
de zero. Qual a relação dessa
temperaturas com os números inteiros?
Quando falamos acima de zero, estamos
referir aos números positivos e quand
falamos dos números abaixo de zer
estamos a referir aos números negativos.
10° C ------------- 10° C acima de zero
- 3° C --------------- 3° C abaixo de zero

4. Chamamos a todos os que estão
com o símbolo menos
abaixo de zero.
Os números negativos
antes.
Assim os diferenciamos dos positivos
..., -5, -4, -3, -2, -1
um número não leva sinal
que é
Quando
nenhum
positivo:
antes, entendemos
6= +6 +12=12

6. Altitude
200m
80m 30m

7. Do andar em que se encontra
o elevador do edifício, posso
subir a pisos superiores ou
descer a outros pisos
inferiores:
- 4
+5
•Subo cinco andares:
•Desço quatro andares:

8. O saldo de uma conta do banco
aumenta (+) com os depósitos
e diminui (-) com os
levantamentos.
• A Carminho depositou na sua conta bancária cem euros:
• O Ernesto levantou 200 euros da sua conta bancária:
+ € 100
- € 200

9. + 10 pessoas
O número de pessoas que viajam num
autocarro varia em cada paragem:
•Sobem 10 pessoas:
•Descem 14 pessoas: - 14 pessoas

10. 2 3 4 5
0 1
-1
-2
-3
Cada vez maior
Quando dispostos sobre um eixo, os números relativos
encontram-se ordenados.
Se o eixo é horizontal e orientado da esquerda para a
direita, um número é tanto maior quanto mais para a
direita se encontrar.

11. Da observação da posição relativa de
dois números num eixo resultam
algumas regras para comparar dois
números diferentes:
•Qualquer número positivo é
maior do que zero.
+ 3 > 0 + 4,5 > 0
+ 8,25 > 0

12. •Zero é maior que qualquer número
negativo.
0 > - 10
•Qualquer número positivo é maior
do que qualquer negativo.
+1 > - 35

13. Para auxiliar na comparação usa sempre a reta numérica.
Que temperatura é a mais baixa: - 5 ºC, - 2 ºC ou + 2 ºC?
- 5 < - 2 < +2
Os números “crescem” da esquerda para a direita. Um
número é tanto maior quanto mais à direita se encontrar.

14.  Depois da representação dos números numa reta numérica é fácil ordená-
los.
 Para escrever os números por ordem crescente, basta-nos lê-los, na
reta numérica, da esquerda para a direita:
-9 < -4 < 0 < 1 < 2 < 4 < 9
Verificamos também que:
 0 (zero) é menor do que qualquer número positivo.
 Qualquer número negativo é menor que zero.
 Qualquer número negativo é menor que qualquer número positivo.
Entre dois números negativos é menor o que estiver mais afastado da
origem.

15. Os números relativos – positivos,
negativos ou o zero – podem ser
representados numa reta por meio de
pontos.
Se quisermos marcar o ponto A correspondente ao número +5,
contamos 5 unidades para a direita de 0 ( zero ).
- O +1
A
+5 +

16. +
- O +1
B
-3
Se quisermos marcar o ponto B
correspondente ao número -3,
contamos 3 unidades para a
esquerda de 0 (zero).

17. O número que corresponde a um ponto do eixo
chamamos abcissa desse ponto.
A
+5 +
- O +1
B
-3
A abcissa de A é +5
A origem tem abcissa zero.
A abcissa de B é -3

18. ou do
| + 800 | = 800
| - 800 | = 800
A distância de um ponto à origem é chamada
número que corresponde esse número.
| | Símbolo que representa valor
absoluto ou módulo de um número

19. |+10|=10
|-10|=10
 -10 é oposto de 10
 +4 é o simétrico de -4
Números que possuem o mesmo módulo
são chamados de opostos ou simétricos.
Números simétricos são dois números que estão à mesma distância de 0.

20. (+2)=(+6)
- (-
Sinais
(-4)
Sinais operacion
posicionais
+( 2)= 6)
(+4)+
ais
Da adição de dois números relativos
com o mesmo sinal, resulta um
número com o mesmo sinal e cujo
valor absoluto é a soma dos valores
absolutos desses números.

21. (-3)+(+2)=(-1)
Da adição de dois números relativos com sinais contrários, resulta
um número com o sinal do que tiver maior valor absoluto. O seu
valor absoluto é a diferença dos valores absolutos desses
números.
Sinais operacionais
Sinais posicionais
(+3)+(-2)=(+1)

22. Será que só existem adições? Então e
a subtração (+2) - (+4) ?

23. Para subtrair dois números inteiros
relativos, adicionamos o aditivo com o
simétrico do subtractivo.
EXEMPLOS:
(+ 3) – (+ 5) = - 2 (+ 3) – (- 3) = + 6
(- 3) – (- 6) = +3 (- 5) – (- 3) = - 2

24. SUBCONJUNTOS DE Z :
Z+ = { 1, 2, 3, ...}  números inteiros positivos
Z - = {..., -3, -2, -1}  números inteiros negativos
Z 0
+ = {0, 1, 2, 3, ...}  números inteiros não negativos
Z 0
- = {..., -3, -2, -1, 0}  números inteiros não positivos