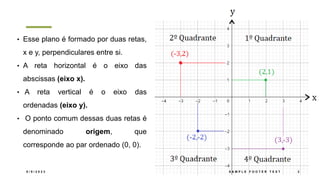
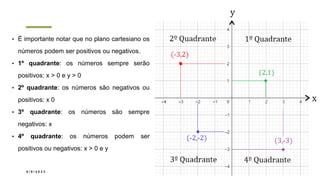
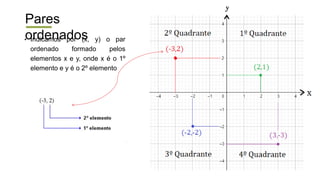
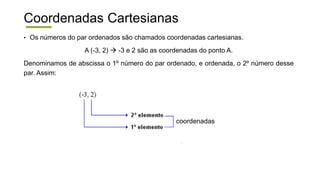
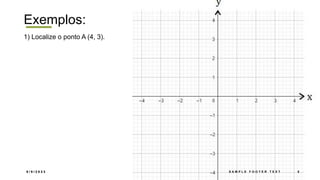
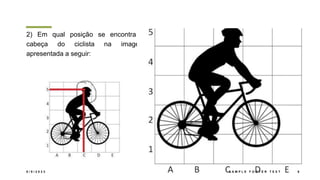
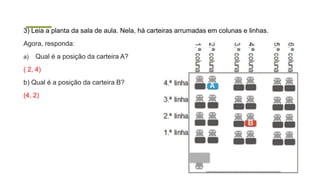
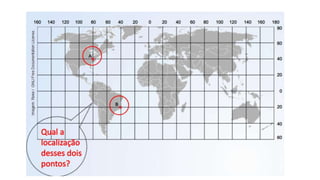
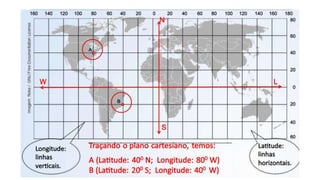
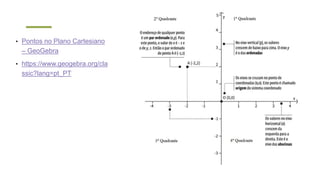
O documento descreve o sistema de coordenadas cartesianas, incluindo: (1) O plano cartesiano é formado pelos eixos x e y perpendiculares, com a origem no ponto (0,0); (2) Pares ordenados (x,y) são usados para localizar pontos no plano, onde x é a abscissa e y é a ordenada; (3) Exemplos mostram como localizar pontos usando suas coordenadas cartesianas.

1. Transformações
geométricas
e simetria
P O L Í G O N O S E S I S T E M A D E
C O O R D E N AD A S

2. Plano Cartesiano
• Foi o filósofo e matemático francês René
Descartes quem imaginou pela primeira
vez um sistema para localizar qualquer
ponto em um plano, o chamado sistema
coordenado.
• As coordenadas cartesianas foram criadas
com objetivo de localizar pontos num
plano.
• O plano cartesiano aceita qualquer unidade
de medida e qualquer intervalo entre
valores.
8 / 9 / 2 0 2 3 S A M P L E F O O T E R T E X T 2

3. • Esse plano é formado por duas retas,
x e y, perpendiculares entre si.
• A reta horizontal é o eixo das
abscissas (eixo x).
• A reta vertical é o eixo das
ordenadas (eixo y).
• O ponto comum dessas duas retas é
denominado origem, que
corresponde ao par ordenado (0, 0).
8 / 9 / 2 0 2 3 S A M P L E F O O T E R T E X T 3

4. • É importante notar que no plano cartesiano os
números podem ser positivos ou negativos.
• 1º quadrante: os números sempre serão
positivos: x > 0 e y > 0
• 2º quadrante: os números são negativos ou
positivos: x 0
• 3º quadrante: os números são sempre
negativos: x
• 4º quadrante: os números podem ser
positivos ou negativos: x > 0 e y
8 / 9 / 2 0 2 3 S A M P L E F O O T E R T E X T 4

5. Pares
ordenados
• Indicamos por (x, y) o par
ordenado formado pelos
elementos x e y, onde x é o 1º
elemento e y é o 2º elemento

6. Coordenadas Cartesianas
• Os números do par ordenados são chamados coordenadas cartesianas.
A (-3, 2)  -3 e 2 são as coordenadas do ponto A.
Denominamos de abscissa o 1º número do par ordenado, e ordenada, o 2º número desse
par. Assim:
coordenadas

7. Localização de um Ponto
É comum associar a malha quadriculada ao plano cartesiano para facilitar ao plano
cartesiano a localização de pontos. Para localizar um ponto no plano cartesiano
procedemos da maneira a seguir:
✓ O primeiro número do par ordenado está no eixo das abscissas (eixo x).
✓ O segundo número do par ordenado está no eixo das ordenadas (eixo y).
✓ O encontro das retas perpendiculares aos eixos que passam por esses números
determina o ponto a ser localizado.

8. Exemplos:
1) Localize o ponto A (4, 3).
8 / 9 / 2 0 2 3 S A M P L E F O O T E R T E X T 8

9. 2) Em qual posição se encontra a
cabeça do ciclista na imagem
apresentada a seguir:
8 / 9 / 2 0 2 3 S A M P L E F O O T E R T E X T 9

10. 3) Leia a planta da sala de aula. Nela, há carteiras arrumadas em colunas e linhas.
Agora, responda:
a) Qual é a posição da carteira A?
( 2, 4)
b) Qual é a posição da carteira B?
(4, 2)

14. • Pontos no Plano Cartesiano
– GeoGebra
• https://www.geogebra.org/cla
ssic?lang=pt_PT

15. Atividades
1) Desenhe um plano cartesiano e localize os seguintes pontos:
A= (-3,1)
B=(2,3)
C=(-1,-2)
D=(0,0)
E=(4,-3)
F=(3,1)