O documento apresenta um caderno pedagógico complementar de matemática para o 7o ano do ensino fundamental regular. O caderno contém cinco unidades sobre números inteiros, equações do 1o grau, razões e proporções, porcentagem e área e perímetro. Cada unidade inclui explicações dos conceitos, exemplos ilustrativos e exercícios para a prática dos alunos.





















![22
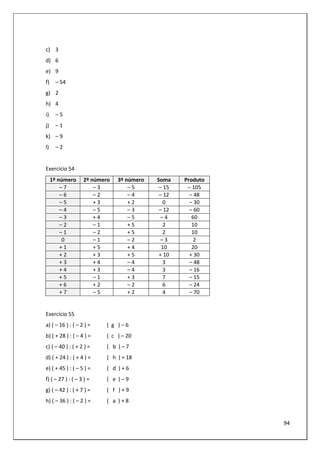
36) Em uma cidade dos Estados Unidos, a temperatura mais fria no inverno foi de – 70
C e a mais
quente no verão foi de 320
C. Qual é a diferença entre a temperatura mais quente e a temperatura
mais fria?
37) Quantos anos viveu uma pessoa que nasceu no ano 35 a.C. e morreu no ano 47 d.C.?
38) Escolha a alternativa que resolve o seguinte problema:
O professor de Ciências fez uma experiência em que a temperatura foi medida três vezes. A segunda
leitura foi de 8 graus a menos que a primeira, e a terceira foi de 10 graus a menos que a segunda. Se
a primeira leitura indicou 7 graus, qual foi a última temperatura indicada?
a) 7 graus b) 8 graus c) – 11 graus d) – 1 graus
• Eliminando os Parênteses
Sinal (+) antes dos parênteses
Exemplos:
a) + (– 4 + 6) = – 4 + 6 = 2
b) + (8 + 2 – 3) = 8 + 2 – 3 = 7
Sinal (–) antes dos parênteses
Exemplos:
a) – (12 – 4 + 2) = – 12 + 4 – 2 = – 10
b) – (– 11 + 1 – 5) = + 11 – 1 + 5 = 15
c) – (– 4 – 5) = 4 + 5 = 9 [Significa: o oposto de (– 4 – 5) é + 9]
d) – (+ 7 + 3) = – 7 – 3 = – 10 [Significa: o oposto de (+ 7 + 3) é – 10]
EXERCÍCIOS
39) Elimine os parênteses e dê o resultado:
a) + (3 – 2) =
b) + (– 5 + 8) =
c) – (3 – 5 + 7) =
Conserve os
sinais dos
números que
estão dentro dos
parênteses.
Troque os sinais
dos números que
estão dentro dos
parênteses.](https://image.slidesharecdn.com/matemticacaderno-conjuntodosinteiros-220811201434-f5e82bd1/85/MATEMATICA-CADERNO-CONJUNTO-DOS-INTEIROS-pdf-22-320.jpg)
![23
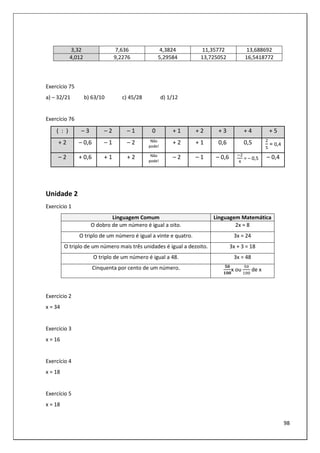
d) + (9 + 6 – 10) =
e) 8 + (– 3 – 3) =
f) 25 – (– 4 – 5) =
g) – 20 – (– 2 + 3) =
h) 100 – (25 – 10 + 5) =
i) 200 + (– 30 + 70 + 40 – 20) =
j) 40 – (– 30 + 10) – (– 5 + 10 + 15) =
k) 25 + (15 – 50) + (– 20 – 10) =
• Expressões numéricas
SE LIGA NESSA!
Devemos respeitar a seguinte ordem, para
resolvermos as expressões numéricas:
1º Parênteses ( );
2º Colchetes [ ];
3º Chaves { }.
Exemplos:
a) 8 + (+ 6 – 1) – (– 4 + 2 – 5) =
= 8 + 6 – 1 + 4 – 2 + 5 =
= 23 – 3 =
= 20
b) 35 + [– 4 + 1 – (– 3 + 6) ]=
= 35 + [– 4 + 1 + 3 – 6 ]=
= 35 – 4 + 1 + 3 – 6=
= 39 – 10=
= 29
c) –15 + {+ 3 – [ 2 – (– 7 + 10)]} =
= –15 + {+ 3 – [2 + 7 – 10]} =
= –15 + {+ 3 – 2 – 7 + 10} =
= –15 + 3 – 2 – 7 + 10 =
= – 24 + 13 = – 11
Veja que existe um
sinal (+) positivo e
outro negativo (–)
antes dos parênteses!
Ah, quando o sinal é positivo
(+), não trocamos os sinais
dos números que estão nos
parênteses, mas quando o
sinal é negativo (–),
trocamos todos os sinais dos
números que estão nos
parênteses!
Lucas, essa regra
vale para os
parênteses,
colchetes e chaves.](https://image.slidesharecdn.com/matemticacaderno-conjuntodosinteiros-220811201434-f5e82bd1/85/MATEMATICA-CADERNO-CONJUNTO-DOS-INTEIROS-pdf-23-320.jpg)
![24
EXERCÍCIOS
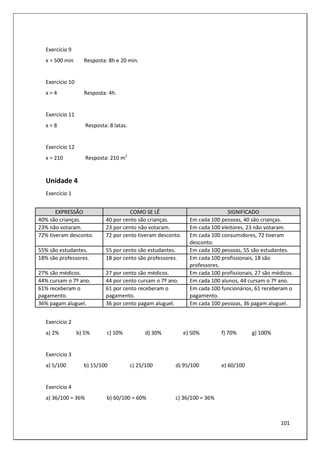
40) Observe a figura:
A cidade de Gramado está localizada no Rio Grande do
Sul, região sul do Brasil. Considerando a tabela ao lado,
que mostra a temperatura em julho de 2013, responda às
questões que seguem.
a) A diferença entre a temperatura máxima e a mínima
de cada dia é:
Quarta-feira = ................ Quinta-feira = ..................
Sexta-feira =................... Sábado = .........................
Domingo = .......................
b) Qual o dia em que fez mais frio?
............................................................................................
c) Qual dia apresentou maior diferença de temperatura?
............................................................................................
d) Qual dia apresentou menor diferença de temperatura?
...........................................................................................
(Disponível em: <http://www.climatempo.com.br/previsao-do-tempo/cidade/780/gramado-rs>. Acesso em: 19/07/2013)
41) Resolva as seguintes expressões numéricas:
a) 15 – (8 – 7) + (9 – 4) =
b) 12 – { – 3 + [1 + (+ 2 – 9) – 8] + 5} =
42) Calcule a soma das diferenças entre a temperatura máxima e a temperatura mínima de cada
dia na cidade de Petrópolis, no Rio de Janeiro, em 2013, nos dias mostrados na figura a seguir:](https://image.slidesharecdn.com/matemticacaderno-conjuntodosinteiros-220811201434-f5e82bd1/85/MATEMATICA-CADERNO-CONJUNTO-DOS-INTEIROS-pdf-24-320.jpg)
























![49
c)
5
= 5
d)
5
= 6
e)
5
= – 9
Observe as resoluções das equações:
Exemplo4:
12x – 5 = 10x + 4 (O termo com x deve passar para o 1º membro)
12x – 10x = 4 + 5 (10x mudou e virou – 10x) e (– 5 mudou de membro e virou + 5).
(12 – 10)x = 9 (Reduz os termos semelhantes: 12x – 10x = 2x).
2x = 9
x = (2 mudou de membro. Multiplicando em um membro, passa a dividir no outro membro).
x = 4,5 S = {4,5} (Conjunto Solução).
Exemplo5:
3x + x – 4 = x – 2x + 16 (Os termos com x devem passar para o 1º membro)
3x + x – x + 2x = 16 + 4 (x virou – x) e (– 2x virou + 2x)
(3 + 1 – 1 + 2)x = 20 (Reduz os termos semelhantes: 3x + x – x + 2x = 5x)
5x = 20
x = (5 mudou de membro. Multiplicando em um membro, passa a dividir no outro)
x = 4 S = {4} (Conjunto Solução).
Exemplo 6:
30 = 2x + 2 2x + 2 = 30 (Pela Propriedade Simétrica)
2x + 2 = 30
2x = 30 – 2
2x = 28
x =
x = 14 S = {14} (Conjunto Solução)
Exemplo7:
– 8x = – 32 [Multiplicamos ambos os membros por (– 1)]
(– 8x) . (– 1) = (– 32) . (– 1) [Usamos a regra de sinais da multiplicação: (–).(–) =(+)]
8x = 32
x =
x = 4 S = {4} (Conjunto Solução)
Vamos ver
mais alguns
exemplos!](https://image.slidesharecdn.com/matemticacaderno-conjuntodosinteiros-220811201434-f5e82bd1/85/MATEMATICA-CADERNO-CONJUNTO-DOS-INTEIROS-pdf-49-320.jpg)







































![91
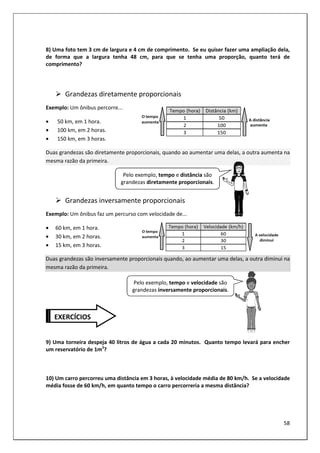
Exercício 39
a) 1
b) 3
c) – 5
d) 5
e) 2
f) 34
g) – 21
h) 80
i) 260
j) 40
k) – 40
Exercício 40
a) Quarta-feira = 12 graus / Quinta-feira = 15 graus / Sexta-feira = 15 graus / Sábado = 13 graus /
Domingo = 8 graus.
b) Quarta-feira.
c) Quinta-feira e sexta-feira.
d) Domingo.
Exercício 41
a) 15 – (8 – 7) + (9 – 4) =
15 – 1 + 5 = 19
b) 12 – {– 3 + [1 + (+ 2 – 9) – 8] + 5} =
12 – {– 3 + [1 – 7 – 8] + 5} =
12 – {– 3 + [– 14] + 5} =
12 – {– 3 –14 + 5} =
12 – {– 12} =
12 + 12 = 24
Exercício 42
(12 – 8) + (16 – 10) + (16 – 12) + (17 – 11) + (18 – 9) = 4 + 6 + 4 + 6 + 9 = 29
Exercício 43
a) +
b) –](https://image.slidesharecdn.com/matemticacaderno-conjuntodosinteiros-220811201434-f5e82bd1/85/MATEMATICA-CADERNO-CONJUNTO-DOS-INTEIROS-pdf-91-320.jpg)