O documento descreve três estudos de caso sobre sistemas dinâmicos modelados por equações diferenciais ordinárias (EDOs). O primeiro caso analisa o modelo presa-predador de Volterra-Lotka usando métodos numéricos com passos fixo e adaptativo. O segundo caso estuda o modelo atmosférico de Lorenz usando o método de Runge-Kutta. O terceiro caso descreve uma fonte intermitente modelada por uma EDO com variável booleana.

1. UFSC/CTC/EQA – EQA5312 Análise e Simulação de Processos
Prof. Ricardo A. F. Machado | Prof. Natan Padoin
Passo Fixo x Passo Adaptativo (Estudo de Caso 1)
Considere o problema presa x predador desenvolvido pelo matemático italiano Vito Volterra e o biólogo
americano Alfred Lotka:
𝑑𝑥
𝑑𝑡
= 𝑎𝑥 − 𝑏𝑥𝑦
𝑑𝑦
𝑑𝑡
= −𝑐𝑦 + 𝑑𝑥𝑦
onde 𝑥 e 𝑦 representam o número de presas e predadores, respectivamente, 𝑎 é a taxa de crescimento
das presas, 𝑐 é a taxa de morte dos predadores e 𝑏 e 𝑑 são taxas que caracterizam o efeito da interação
presa x predador na morte da presa e crescimento do predador, respectivamente.
Busca-se resolver o sistema de EDOs considerando o seguinte conjunto de parâmetros: 𝑎 = 1,2, 𝑏 = 0,6,
𝑐 = 0,8 e 𝑑 = 0,3; condições iniciais: 𝑥0 = 2 e 𝑦0 = 1; integrar no intervalo 0 ≤ 𝑡 ≤ 30.
A solução do modelo através do solver ode45 do MATLAB (método com passo de tempo adaptativo)
resulta nos perfis obtidos na Figura 1. Claramente, há uma amplitude constante ao longo dos ciclos.
Figura 1 – Solver ode45: (a) intensidade x t e (b) t x t.
Por outro lado, quando o método de Euler explícito é empregado, com passo t = 0,0625, tem-se o
resultado apresentado na Figura 2. Nesse caso, há uma incoerência nos perfis obtidos, uma vez que a
amplitude tende a aumentar continuamente ao longo dos ciclos. Tal comportamento pode ser
corroborado por meio dos retratos de fases apresentados na Figura 3.
Qual seria o comportamento obtido caso o método de Runge-Kutta de quarta ordem fosse aplicado (com
o mesmo t)? Tarefa para casa!
0 10 20 30 40
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
Solver ode45
Tempo
(-)
Presa
Predador
0 10 20 30 40
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Tempo
Passodetempo
(a) (b)

2. Figura 2 – Método de Euler explícito (t = 0,0625).
Figura 3 – Retratos de fases: (a) solver ode45, (b) método de Euler explícito.
Este problema pode ser estudado no MATLAB através do seguinte código:
function volterra_lotka_comparacao
clear all;
clc;
close all;
global a b c d
a = 1.2;
b = 0.6;
c = 0.8;
d = 0.3;
dt = 0.0625;
N = 640;
0 5 10 15 20 25 30 35 40
0
2
4
6
8
10
12
14
Tempo
(-)
Presa
Predador
0 2 4 6
0.5
1
1.5
2
2.5
3
3.5
4
x
y
0 5 10 15
0
1
2
3
4
5
6
7
8
x
y
(a) (b)
0
2
4
6
0
2
4
0
10
20
30
40
xy
t
0
5
10
15
0
5
10
0
10
20
30
40
xy
t
0
2
4
6
0
2
4
0
10
20
30
40
xy
t
0
5
10
15
0
5
10
0
10
20
30
40
xy
t

3. time(1) = 0;
x(1) = 2;
y(1) = 1;
for n = 1:N
time(n+1) = time(n) + dt;
x(n+1) = x(n) + dt * (a * x(n) - b * x(n) * y(n));
y(n+1) = y(n) + dt * (-c * y(n) + d * x(n) * y(n));
end
[t,u] = ode45(@vl, [0 40], [2 1]);
stepsize = diff([0; t]);
subplot(1,2,1)
plot(t,u(:,1),'r',t,u(:,2),'--b','LineWidth',1.5)
title('Solver ode45')
xlabel('Tempo (min)')
ylabel('(-)')
grid on
legend('Presa','Predador','Location','Best')
subplot(1,2,2)
plot(t,stepsize,'k','LineWidth',1.5)
xlabel('Tempo')
ylabel('Passo de tempo (min)')
grid on
% subplot(1,2,1)
% plot(u(:,1),u(:,2),'LineWidth',2)
% xlabel('x')
% ylabel('y')
% grid on
%
% subplot(1,2,2)
% plot(x,y,'r','LineWidth',2)
% xlabel('x')
% ylabel('y')
% grid on
figure
plot(time,x,'r',time,y,'--b','LineWidth',1.5)
xlabel('Tempo')
ylabel('(-)')
grid on
legend('Presa','Predador','Location','Best')
end
function dudt = vl(t,u)
global a b c d

4. dudt = [a * u(1) - b * u(1) * u(2);
-c * u(2) + d * u(1) * u(2)];
end
Passo Fixo x Passo Adaptativo (Estudo de Caso 2)
Outro problema interessante foi desenvolvido pelo meteorologista americano Edward Lorenz, conhecido,
portanto, como equações de Lorenz, para a avaliação da fluidodinâmica atmosférica:
𝑑𝑥
𝑑𝑡
= 𝜎(𝑦 − 𝑥)
𝑑𝑦
𝑑𝑡
= 𝑥(𝜌 − 𝑧) − 𝑦
𝑑𝑧
𝑑𝑡
= 𝑥𝑦 − 𝛽𝑧
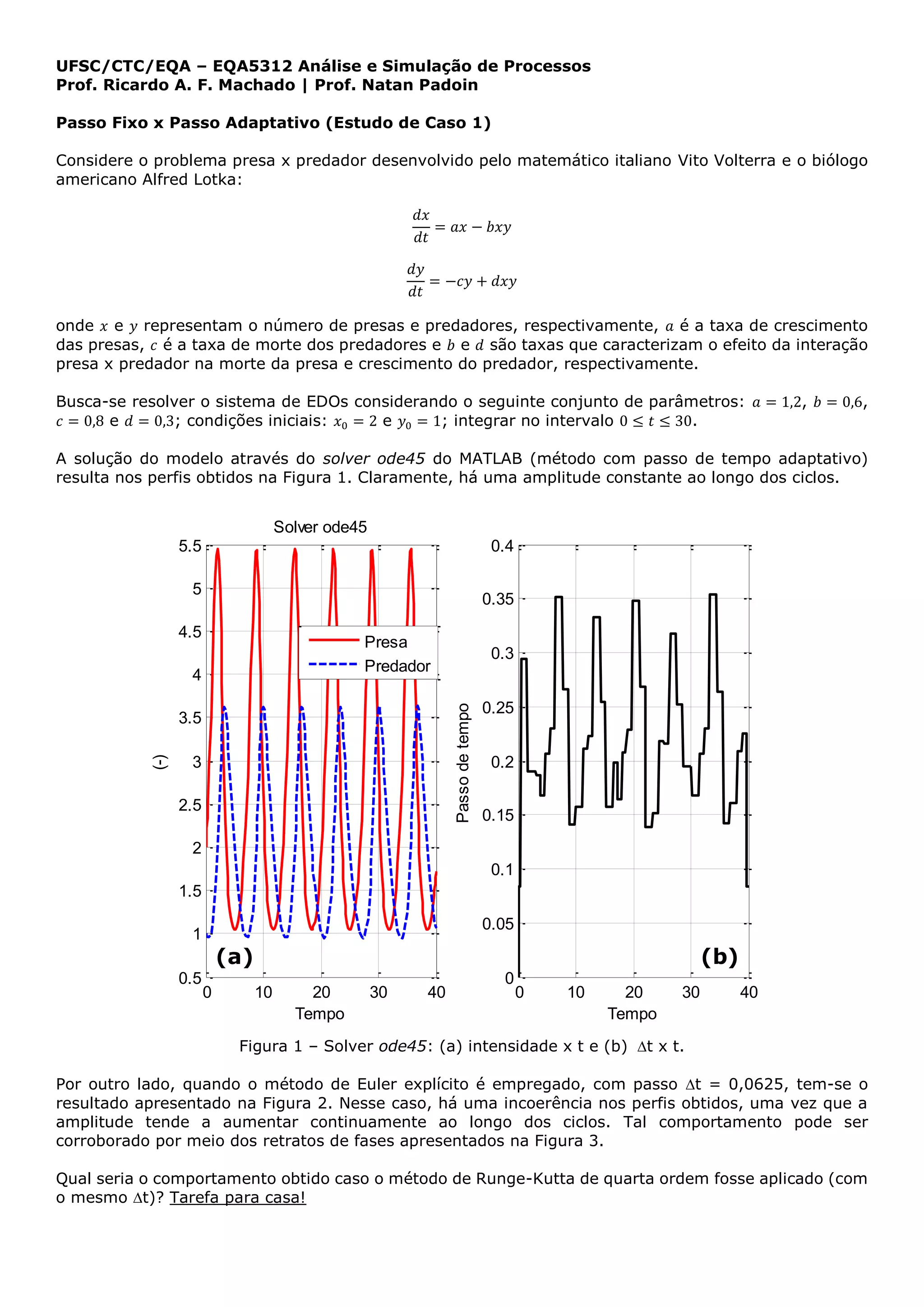
Tal modelo relaciona a intensidade de escoamento atmosférico 𝑥 com as variações de temperatura 𝑦 e 𝑧
nas direções horizontal e vertical, respectivamente. A Figura 4 apresenta o comportamento caótico obtido
com a solução do modelo por meio do método de Runge-Kutta de quarta ordem (RK4), considerando o
seguinte conjunto de parâmetros: 𝜎 = 10, 𝛽 = 8/3, 𝜌 = 28; 𝑥0 = 𝑦0 = 𝑧0 = 5. Nota-se, ainda, que uma
pequena variação na condição inicial para 𝑥 (𝑥0 = 5,001) induz uma significativa mudança na dinâmica do
sistema.
Figura 4 – Comportamento caótico para o escoamento atmosférico segundo o modelo de Lorenz.
Este modelo pode ser estudado a partir do seguinte código na linguagem MATLAB:
clear all;
clc;
close all;
%% Parâmetros do modelo
global rho sigma beta
rho = 28;
sigma = 10;
beta = 8/3;
0 2 4 6 8 10 12 14 16 18 20
-20
-15
-10
-5
0
5
10
15
20
Tempo
x
x0
=5
x0
=5.001

5. %% Handles
fx = @(t,x,y,z) sigma * (y - x);
fxp = @(t,x,y,z) sigma * (y - x);
fy = @(t,x,y,z) x * (rho - z) - y;
fz = @(t,x,y,z) x * y - beta * z;
%% Parâmetros numéricos
dt = 0.03125;
tf = 20;
N = ceil(tf/dt);
%% Inicialização
x(1) = 5;
y(1) = 5;
z(1) = 5;
xp(1) = 5.001;
t(1) = 0;
%% Método RK4
for n = 1:N
t(n+1) = t(n) + dt;
k1x = fx(t(n) ,x(n) ,y(n) ,z(n) );
k1y = fy(t(n) ,x(n) ,y(n) ,z(n) );
k1z = fz(t(n) ,x(n) ,y(n) ,z(n) );
k2x = fx(t(n)+dt/2,x(n)+dt/2*k1x,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k2y = fy(t(n)+dt/2,x(n)+dt/2*k1x,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k2z = fz(t(n)+dt/2,x(n)+dt/2*k1x,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k3x = fx(t(n)+dt/2,x(n)+dt/2*k2x,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k3y = fy(t(n)+dt/2,x(n)+dt/2*k2x,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k3z = fz(t(n)+dt/2,x(n)+dt/2*k2x,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k4x = fx(t(n)+dt ,x(n)+dt *k3x,y(n)+dt *k3y,z(n)+dt *k3z);
k4y = fy(t(n)+dt ,x(n)+dt *k3x,y(n)+dt *k3y,z(n)+dt *k3z);
k4z = fz(t(n)+dt ,x(n)+dt *k3x,y(n)+dt *k3y,z(n)+dt *k3z);
x(n+1) = x(n) + dt/6 * (k1x + 2*k2x + 2*k3x + k4x);
y(n+1) = y(n) + dt/6 * (k1y + 2*k2y + 2*k3y + k4y);
z(n+1) = z(n) + dt/6 * (k1z + 2*k2z + 2*k3z + k4z);
end
for n = 1:N
t(n+1) = t(n) + dt;
k1xp = fxp(t(n) ,xp(n) ,y(n) ,z(n) );

6. k1y = fy(t(n) ,xp(n) ,y(n) ,z(n) );
k1z = fz(t(n) ,xp(n) ,y(n) ,z(n) );
k2xp = fxp(t(n)+dt/2,xp(n)+dt/2*k1xp,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k2y = fy(t(n)+dt/2 ,xp(n)+dt/2*k1xp,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k2z = fz(t(n)+dt/2 ,xp(n)+dt/2*k1xp,y(n)+dt/2*k1y,z(n)+dt/2*k1z);
k3xp = fxp(t(n)+dt/2,xp(n)+dt/2*k2xp,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k3y = fy(t(n)+dt/2 ,xp(n)+dt/2*k2xp,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k3z = fz(t(n)+dt/2 ,xp(n)+dt/2*k2xp,y(n)+dt/2*k2y,z(n)+dt/2*k2z);
k4xp = fxp(t(n)+dt ,xp(n)+dt *k3xp,y(n)+dt *k3y,z(n)+dt *k3z);
k4y = fy(t(n)+dt ,xp(n)+dt *k3xp,y(n)+dt *k3y,z(n)+dt *k3z);
k4z = fz(t(n)+dt ,xp(n)+dt *k3xp,y(n)+dt *k3y,z(n)+dt *k3z);
xp(n+1) = xp(n) + dt/6 * (k1xp + 2*k2xp + 2*k3xp + k4xp);
y(n+1) = y(n) + dt/6 * (k1y + 2*k2y + 2*k3y + k4y);
z(n+1) = z(n) + dt/6 * (k1z + 2*k2z + 2*k3z + k4z);
end
%% Resposta gráfica
figure('Name','Equações de Lorentz','Number','off')
plot(t,x,'r',t,xp,':b','LineWidth',2.5)
xlabel('Tempo')
ylabel('x')
grid on
legend('x_0=5','x_0=5.001','Location','Best')
Passo Fixo x Passo Adaptativo (Estudo de Caso 3)
Nem sempre, porém, o solver do MATLAB, com passo adaptativo, tem um bom desempenho.
Exemplo:
Pliny, filósofo natural romano, possuía uma fonte intermitente em seu jardim, ilustrada na imagem
abaixo:
Água é alimentada no tanque com vazão constante 𝑄𝑖𝑛 e o enche até atingir a altura ℎℎ𝑖𝑔ℎ. Nesse ponto,
a água é sifonada do tanque através de um duto circular, produzindo um chafariz na saída. Esse efeito
se mantém até que a água atinge o nível 𝑦𝑙𝑜𝑤, quando o sifão é preenchido com ar e o chafariz é extinto.
O ciclo se repete, uma vez que o nível atinge a altura 𝑦ℎ𝑖𝑔ℎ e o chafariz é novamente produzido.
Um balanço material global neste tanque fornece:

7. 𝑑𝑉
𝑑𝑡
= 𝑄𝑖𝑛 − 𝑄 𝑜𝑢𝑡
onde 𝑉 é o volume (m³). Uma vez que o tanque é cilíndrico, 𝑉 = 𝜋𝑅𝑡
2
𝑦. Além disso, quando o sifão atua,
a vazão na saída (𝑄 𝑜𝑢𝑡) pode ser calculada através da seguinte equação, baseada na lei de Torricelli:
𝑄 𝑜𝑢𝑡 = 𝐶√2𝑔𝑦𝜋𝑟2
Portanto, tem-se:
𝑑𝑦
𝑑𝑡
=
𝑄𝑖𝑛 − 𝐶√2𝑔𝑦𝜋𝑟2
𝜋𝑅𝑡
2
Quando o sifão não atua, o segundo termo no numerador deve ser igualado à zero. Assim, é conveniente
multiplicar tal termo da EDO por uma variável booleana 𝑠:
𝑑𝑦
𝑑𝑡
=
𝑄𝑖𝑛 − 𝑠 × 𝐶√2𝑔𝑦𝜋𝑟2
𝜋𝑅𝑡
2
sendo que 𝑠 = 0 quando 𝑦 ≤ 𝑦𝑙𝑜𝑤 e 𝑠 = 1 quando 𝑦 ≥ 𝑦ℎ𝑖𝑔ℎ.
Deseja-se resolver o modelo utilizando o seguinte conjunto de parâmetros: 𝑅𝑡 = 0,05 𝑚, 𝑟 = 0,007 𝑚, 𝑦𝑙𝑜𝑤 =
0,025 𝑚, 𝑦ℎ𝑖𝑔ℎ = 0,1 𝑚, 𝐶 = 0,6, 𝑔 = 9,81 𝑚/𝑠², 𝑄𝑖𝑛 = 50 × 10−6
𝑚3
/𝑠.
Ao se resolver a EDO por meio dos solvers ode45 e ode23s do MATLAB, obtém-se os resultados
apresentados nas Figuras 5 e 6. O resultado está claramente equivocado, uma vez que a amplitude não
se mantém constante quando se utiliza os solvers com passo de tempo adaptativo. Isso acontece devido
à descontinuidade da EDO quando a variável 𝑠 é alternada entre 0 e 1. Já quando se utiliza um método
de passo fixo, como Euler explícito, a amplitude mantém-se constante ao longo dos ciclos, como se pode
observar na Figura 7.
Figura 5 – Solver ode45: (a) h x t e (b) t x t.
0 50 100
0
0.02
0.04
0.06
0.08
0.1
0.12
Solver ode45
Tempo (s)
Nível(m)
0 50 100
0
0.5
1
1.5
2
2.5
Tempo (s)
Passodetempo(s)
(a) (b)

8. Figura 6 – Solver ode23s: (a) h x t e (b) t x t.
Figura 7: Método de Euler explícito (t = 0,001 s).
Este caso pode ser estudado no MATLAB através do seguinte código:
function pliny
clear all;
clc;
close all;
global s rt yh yl r qin c g
0 50 100
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
Solver ode23s
Tempo (s)
Nível(m)
0 50 100
0
1
2
3
4
5
6
7
8
9
10
Tempo (s)
Passodetempo(s)
(a)
(b)
0 10 20 30 40 50 60 70 80 90 100
0
0.02
0.04
0.06
0.08
0.1
0.12
Euler Explícito
Tempo (s)
Nível(m)

9. rt = 0.05;
r = 0.007;
yh = 0.1;
yl = 0.025;
c = 0.6;
qin = 50e-6;
g = 9.81;
dt = 0.001;
N = 99999;
time(1) = 0;
x(1) = 0;
for n = 1:N
if x(n) <= yl
s = 0;
elseif x(n) >= yh
s = 1;
end
time(n+1) = time(n) + dt;
x(n+1) = x(n) + dt * ((qin - s * c * sqrt(2 * g * x(n)) * pi * r ^
2) / (pi * rt ^ 2));
end
[t,u] = ode23s(@fonte, [0 100], 0);
stepsize = diff([0; t]);
subplot(1,2,1)
plot(t,u(:,1),'r','LineWidth',1.5)
title('Solver ode23s')
xlabel('Tempo (s)')
ylabel('Nível (m)')
grid on
subplot(1,2,2)
plot(t,stepsize,'k','LineWidth',1.5)
xlabel('Tempo (s)')
ylabel('Passo de tempo (s)')
grid on
figure
plot(time,x,'b','LineWidth',1.5)
title('Euler Explícito')
xlabel('Tempo (s)')
ylabel('Nível (m)')
grid on
end
function dudt = fonte(t,u)

10. global s rt yh yl r qin c g
if u(1) <= yl
s = 0;
elseif u(1) >= yh
s = 1;
end
qout = s * c * sqrt(2 * g * u(1) * pi * r ^ 2);
dudt = (qin - qout) / (pi * rt ^ 2);
end
Passo Fixo x Passo Adaptativo (Estudo de Caso 4)
Considere, agora, o problema de três reatores de mistura perfeita com escoamento contínuo (CSTRs)
conectados em série:
Em cada reator, mantido a volume constante, temos uma reação química elementar de primeira ordem,
em fase líquida (consumo da espécie química A).
O modelo matemático dinâmico para esse processo é, então, representado por um sistema de três
equações diferenciais ordinárias lineares acopladas:
𝑑
𝑑𝑡
(𝐶𝐴,1) =
𝑞
𝑉1
(𝐶𝐴,𝑒 − 𝐶𝐴,1) − 𝑘1 𝐶𝐴,1
𝑑
𝑑𝑡
(𝐶𝐴,2) =
𝑞
𝑉2
(𝐶𝐴,1 − 𝐶𝐴,2) − 𝑘2 𝐶𝐴,2
𝑑
𝑑𝑡
(𝐶𝐴,3) =
𝑞
𝑉3
(𝐶𝐴,2 − 𝐶𝐴,3) − 𝑘3 𝐶𝐴,3
Submetido às seguintes condições iniciais:
𝐶𝐴,1(𝑡 = 𝑡0) = 𝐶𝐴,1,0
𝐶𝐴,2(𝑡 = 𝑡0) = 𝐶𝐴,2,0
𝐶𝐴,3(𝑡 = 𝑡0) = 𝐶𝐴,3,0
Na solução do modelo, pode-se considerar o seguinte conjunto de parâmetros: 𝑉1 = 𝑉2 = 𝑉3 = 100 𝐿, 𝑞 =
100 𝐿/𝑚𝑖𝑛, 𝑘1 = 0,1 𝑚𝑖𝑛−1
, 𝑘2 = 0,05 𝑚𝑖𝑛−1
, 𝑘3 = 0,2 𝑚𝑖𝑛−1
e 𝐶𝐴,𝑒 = 10 𝑚𝑜𝑙/𝐿. Além disso, assume-se que 𝐶𝐴,1,0 =
𝐶𝐴,2,0 = 𝐶𝐴,3,0 = 0. Obtém, assim, o seguinte resultado através do solver ode45 (MATLAB):

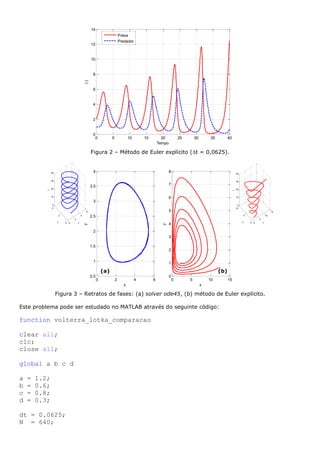
11. Figura 8 – (a) 𝐶𝐴,𝑖 x t, (b) t x t e (c) retrato de fases.
O problema pode ser estudado no MATLAB através do seguinte código:
function tanques_serie_odesolver
clear all;
clc;
close all;
[t,u] = ode45(@tanques, [0 10], [0 0 0]);
stepsize = diff([0; t]);
subplot(1,3,1)
plot(t,u(:,1),':',t,u(:,2),'--',t,u(:,3),'LineWidth',1.5)
xlabel('Tempo (min)')
ylabel('Concentração (mol/L)')
grid on
legend('Tanque 1','Tanque 2','Tanque 3','Location','Best')
subplot(1,3,2)
plot(t,stepsize,'k','LineWidth',1.5)
xlabel('Tempo (min)')
ylabel('Passo de tempo (min)')
grid on
subplot(1,3,3)
plot3(u(:,1),u(:,2),u(:,3),'r','LineWidth',2.5)
xlabel('Ca_1')
ylabel('Ca_2')
zlabel('Ca_3')
grid on
end
0 5 10
0
1
2
3
4
5
6
7
8
9
10
Tempo (min)
Concentração(mol/L)
Tanque 1
Tanque 2
Tanque 3
0 5 10
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Tempo (min)
Passodetempo(min)
0
5
10
0
5
10
0
1
2
3
4
5
6
7
8
Ca1
Ca2
Ca
3
(a)
(b)
(c)

12. function dudt = tanques(t,u)
k1 = 0.1;
k2 = 0.05;
k3 = 0.2;
V1 = 100;
V2 = 100;
V3 = 100;
q = 100;
Cae = 10;
dudt = [(q/V1) * (Cae - u(1)) - k1 * u(1);
(q/V2) * (u(1) - u(2)) - k2 * u(2);
(q/V3) * (u(2) - u(3)) - k3 * u(3)];
end
Problemas Stiff
Um problema stiff clássico é o de van der Pol, dado pela EDO:
𝑑2
𝑦1
𝑑𝑡2
− 𝜇(1 − 𝑦1
2)
𝑑𝑦1
𝑑𝑡
+ 𝑦1 = 0
Tal equação de segunda ordem pode ser decomposta em duas equações de primeira ordem:
𝑑𝑦1
𝑑𝑡
= 𝑦2
𝑑𝑦2
𝑑𝑡
= 𝜇(1 − 𝑦1
2)𝑦2 − 𝑦1
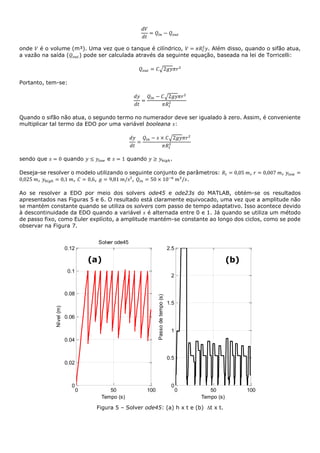
Quando 𝜇 = 1, o modelo pode ser prontamente resolvido utilizando o solver ode45 (passo adaptativo),
resultado no perfil apresentado na Figura 9 e nos retratos de fases da Figura 10.
Figura 9 – Problema de van der Pol: (a) perfil de 𝑦 e (b) passo de tempo para 𝜇 = 1.
0 5 10 15 20
-3
-2
-1
0
1
2
3
Tempo
y
 = 1
y1
y2
0 5 10 15 20
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
0.18
0.2
Tempo
Passodetempo
(a)
(b)

13. Figura 10 – Retratos de fases para 𝜇 = 1.
Quando 𝜇 = 1000, porém, tem-se um problema stiff e o solver ode45 já não é mais adequado. Nesse
caso, pode-se optar pelo solver ode23s, resultando no perfil apresentado na Figura 11 e nos retratos de
fases apresentados na Figura 12.
Figura 11 – Problema de van der Pol: (a) perfil de 𝑦 e (b) passo de tempo para 𝜇 = 1000.
-4 -2 0 2 4
-3
-2
-1
0
1
2
3
y1
y
2
-5
0
5
-5
0
5
0
5
10
15
20
y1
y2
t
0 2000 4000 6000
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
Tempo
y
1
 = 1000
0 2000 4000 6000
0
5
10
15
20
25
30
35
40
45
50
Tempo
Passodetempo
(a)
(b)

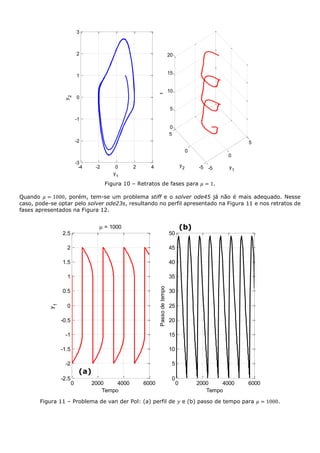
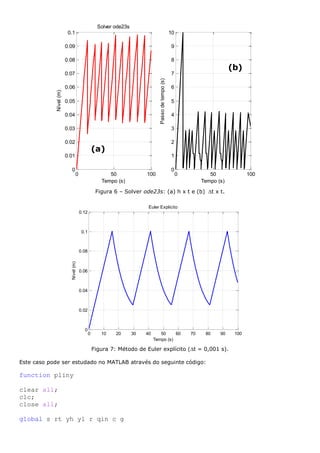
14. Figura 12 – Retratos de fases para 𝜇 = 1000.
O problema pode ser estudado no MATLAB através do seguinte código:
function vanderpol
clear all;
clc;
close all;
[t,y] = ode45(@vdp,[0 20],[1 1]);
stepsize = diff([0; t]);
subplot(2,2,1)
plot(t,y(:,1),'r',t,y(:,2),'--b','LineWidth',2.5)
xlabel('Tempo')
ylabel('y_1')
title('mu = 1')
grid on
subplot(2,2,2)
plot(t,stepsize,'k','LineWidth',1.5)
xlabel('Tempo')
ylabel('Passo de tempo')
grid on
subplot(2,2,3)
plot(y(:,1),y(:,2),'LineWidth',2.5)
xlabel('y_1')
ylabel('y_2')
grid on
subplot(2,2,4)
plot3(y(:,1),y(:,2),t,'r','LineWidth',2.5)
xlabel('y_1')
-4 -2 0 2 4
-1500
-1000
-500
0
500
1000
1500
y1
y
2
-5
0
5
-2000
0
2000
0
1000
2000
3000
4000
5000
6000
y1
y2t

15. ylabel('y_2')
zlabel('t')
grid on
end
function dydt = vdp(t,y)
mu = 1;
dydt = [y(2);
mu * (1 - y(1) ^ 2) * y(2) - y(1)];
end