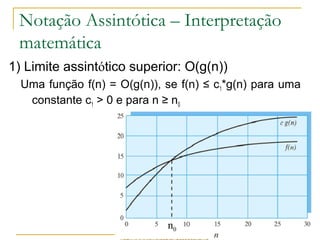
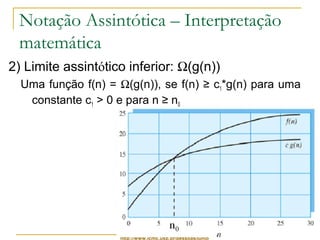
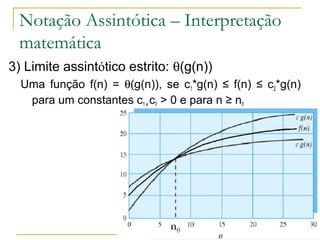
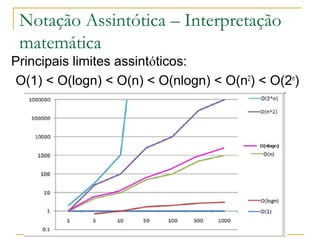
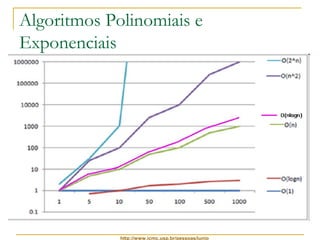
Este documento discute a complexidade de algoritmos e a notação assintótica. Apresenta como a análise de complexidade de algoritmos reduz um algoritmo a uma função matemática que representa o número de instruções executadas em função do tamanho da entrada. Explora os conceitos de limite assintótico superior, inferior e estrito e como eles são usados para classificar algoritmos de acordo com sua taxa de crescimento, ignorando constantes e termos de menor ordem.