1. O documento apresenta resolução de exemplos sobre controle adaptativo de sistemas em tempo discreto e contínuo. 2. Inclui modelagem matemática de sistemas lineares e síntese de controladores PID e de dois graus de liberdade usando técnicas de cancelamento e não cancelamento de zeros. 3. Aborda exemplos de sistemas de segunda ordem, determinação de parâmetros de controle, equações de Diophantus e implementação de leis de controle.

1. CONTROLE ADAPTATIVO
RESOLUÇÃO DOS EXEMPLOS E PROBLEMAS
DO CAPÍTULO 3
ALUNO: Pedro Barata Piquia Junior - 2010310025
PROF. : Dr. André Maurício Damasceno Ferreira
ABRIL
2016

2. EXEMPLO 3.1 MODEL-FOLLOWING COM CANCELAMENTO DE ZEROS
Dado o sistema em tempo continuo:
𝑦+𝑦 = u,
Sua função discreta com período de amostragem h = 0.5 seg é
G(z) =
𝑏1𝑧+𝑏0
𝑧²+𝑎1𝑧+𝑎2
=
0.10653(𝑧+0.8467)
𝑧−1 (𝑧−0.6065)
O desafio é sintetizar um controlador com 2 graus de liberdade cujo a função de
transferência desejado é
𝐵𝑚(𝑧)
𝐴𝑚 (𝑧)
=
0.1761 𝑧
𝑧²−1.3205𝑧−0.496
Isso é claro que os polinômios B(z) e A(z) para
𝐵(𝑧)
𝐴(𝑧)
=
𝑏0𝑧+𝑏1
𝑧²+𝑎1𝑧−𝑎2
=
0.10653(𝑧+0.8467)
𝑧−1 (𝑧−0.6065)
São co-primos. Para resolver este exemplo, iremos utilizar o algoritmo 3.1,o objetivo é
cancelar o zero:
PASSO 1: fatorar B como B = B+
B, onde B+
é monico
B(z) = B+
(z)B-
(z) = (z + 0.8467)0.10653
PASSO 2 : encontrar a solução R’ e S com degS>degA de
AR’ + B-
S = A0Am
A equação de Diophantina é então
A(z)(B + z )Rp(z)
𝑅(𝑧)
+ B + z (B − z )
𝐵(𝑧)
S(z) = B+
(z)A0(z)Am(z)
Onde o polinômio em malha fechada deve ser do grau 2n-1 = 3.
→grau{A0(z)} = 0 e obtemos A0(z) = 1.
A equação reduzida de Diophantina é então
A(z)Rp(z) + B-
(z)S(z) = Am(z)
(z2
+a1z+a2)*1+b0(s0z+s1) = z²+ am1z +am2
Ou
(z²-1.607z+0.6065)Rp(z)+0.10653(s0z+s1)= z² - 1.3205z – 0.4966
Equacionando os coeficientes temos:

3. a1 + b0s0 = am1
a2+b0s1=am2
essas equações podem ser resolvidas se b0 ≠ 0. A solução é
s0 =
𝑎𝑚 1−𝑎1
𝑏0
=
−1.3205+1.607
0.10653
= 2.6852
s1 =
𝑎𝑚 2−𝑎2
𝑏0
=
−0.4966+0.6065
0.10653
= 1.0321
O problema do model-following para esse caso é resolvível.
PASSO 3: computar o sinal de controle para a seguinte lei de controle:
Ru = Tuc - Sy
Os polinômios R(z), S(z) e T(z) são
R(z) = B+
= z +
𝑏1
𝑏0
= z + 0.8467
S(z) = s0z + s1 = 2.6852z – 1.0321
T(z) = A0B’m =
𝑏𝑚 0𝑧
𝑏0
=
0.1761 𝑧
0.10653
= 1.6531z
EXEMPLO 3.2 MODEL-FOLLOWING SEM CANCELAMENTO DE ZEROS
Dado o sistema em tempo continuo:
𝑦+𝑦 = u,
Sua função discreta com período de amostragem h = 0.5 seg é
G(z) =
𝑏0𝑧+𝑏1
𝑧²+𝑎1𝑧+𝑎2
=
0.10653(𝑧+0.8467)
𝑧−1 (𝑧−0.6065)
O desafio é sintetizar um controlador com 2 graus de liberdade cuja a função de
transferência desejada seja:
𝑏𝑚 0𝑧+𝑏𝑚 1
𝑧²+𝑎𝑚 1𝑧+𝑎𝑚 2
=
𝐵𝑚(𝑧)
𝐴𝑚 (𝑧)
=
𝛽(𝑧+0.8467)
𝑧²−1.3205𝑧−0.496
Com
β =
𝐴𝑚 (1)
𝐵𝑚(1)
=
1+𝑎𝑚 1+𝑎𝑚 2
𝑏0+𝑏1
= Bmp(z)
β =
1−1.3205−0.496
0.10653+0.0902
= - 4.15
Cujo o ganho em regime permanente é unitário. A equação de diophantina se torna:

4. (z2
+a1z+a2)*(b0z + r1) +(b0z+b1)(s0z + s1) = (z²+ am1z +am2)(z+a0)
Colocando z =
−𝑏1
𝑏0
= - 0.8467 e resolvendo para r1, obtemos:
r1 =
𝑏1
𝑏0
+
𝑏21+𝑎𝑚 1𝑏0𝑏1+𝑎𝑚 2𝑏20 (−𝑏1+𝑎0𝑏0)
𝑏0(𝑏21−𝑎1𝑏0𝑏1+𝑎2𝑏20)
=
𝑎0𝑎𝑚 2𝑏²0+ 𝑎2−𝑎𝑚 2−𝑎0𝑎𝑚 1 𝑏0𝑏1+ 𝑎0+𝑎𝑚 1−𝑎1 ∗𝑏²1
𝑏21−𝑎1𝑏0𝑏1+𝑎2𝑏20
=
𝑎0 −0.496 ∗0.10653²+ −0.6065+0.496−𝑎0∗(−1.3205) ∗0.10653∗0.0902+ 𝑎0−1.3205+1.607 ∗0.09022
0.09022+1.607∗0.10653∗0.0902−0.6065∗0.10653²
Como: grau{A0(z)} = 0 e obtemos A0(z) = 1.
O parâmetro a0 teve seu valor igual a 1, sendo assim temos:
r1 =
−0.496 ∗0.10653²+ −0.6065+0.496−(−1.3205) ∗0.10653∗0.0902+ 1−1.3205+1.607 ∗0.09022
0.09022+1.607∗0.10653∗0.0902−0.6065∗0.10653²
r1 = 0,975
Perceba que o denominador é zero se os polinômios A(z) e B(z) tem um fator
comum, equacionando os coeficientes dos termos z² e z0
na equação diophantina temos:
s0=
𝑏1(𝑎0𝑎𝑚 1−𝑎2−𝑎𝑚 1𝑎1+𝑎21+𝑎𝑚 2−𝑎1𝑎0)
𝑏²1−𝑎1𝑏0𝑏1+𝑎2𝑏²0
+
𝑏0(𝑎𝑚 1𝑎2−𝑎1𝑎2−𝑎0𝑎𝑚 2+𝑎0𝑎2)
𝑏²1−𝑎1𝑏0𝑏1+𝑎2𝑏²0
s0=
0.0902∗(−1.3205+0.6065− −1.3205∗1.607 +1.6072−0.4966−1.607)
0.0902²− −1.607∗0.10653∗0.0902 +(−0.6065∗0.106532)
+
0.10653∗ −1.3205∗ −0.6065 − 1.607∗0.6065 − −0.4966 +(−0.6065))
0.0902²− −1.607∗0.10653∗0.0902 +(−0.6065∗0.106532)
S0= 11,72
s1=
𝑏1(𝑎1𝑎2−𝑎𝑚 1𝑎2+𝑎0𝑎𝑚 2−𝑎0𝑎2)
𝑏²1−𝑎1𝑏0𝑏1+𝑎2𝑏²0
+
𝑏0(𝑎𝑚 2𝑎2− 𝑎²2−𝑎0𝑎𝑚 2𝑎1+𝑎0𝑎2𝑎𝑚 1)
𝑏²1−𝑎1𝑏0𝑏1+𝑎2𝑏²0
s1 =
0.0902∗(1.607∗0.6065−(1.3205∗0.6065)−0.4966+0.6065)
0.0902²− −1.607∗0.10653∗0.0902 +(−0.6065∗0.106532)
0.10653∗(0.4966∗0.6065−0.60652−0.4966∗1.607+0.6065∗1.3205)
0.0902²− −1.607∗0.10653∗0.0902 +(−0.6065∗0.106532)
s1= 1,1259
além disso, é mostrado que:
R(z) = z + r1 = z + 0.975
S(z) = s0z + s1 = 11.72z + 1.1259
T(z) = βA0(z) = β(z+a0) = -4.15(z+1)

5. EXEMPLO 3.3 SISTEMA EM TEMPO CONTÍNUO
O processo discutido nos exemplos 3.1 e 3.2 têm a seguinte função de transferência
G(s) =
𝑏
𝑠(𝑠+𝑎)
Com a = 1 e b = 1. O desenvolvimento dado pelo algoritmo 3.1 vai ser usado para
encontrar um controlador em tempo continuo. Desde que o processo seja de segunda
ordem, o sistema em malha fechada será de terceira ordem e o controlador de grau
mínimo é de primeira ordem. O polinômio Am tem grau 2 (degAm = degA), Bm é uma
constante (degBm = degB) e A0 tem grau 1 (degA0 = 2 - 0 – 1 = 1). Sendo assim:
A0(s) = s+a0
Sendo assim, a função de transferência desejada é:
Bm (s)
Am (s)
=
ω²
s²+2ζωs+ω
Usando os valores informados no exemplo 3.1:
ω = 1rad/s
ζ = 0.7
então:
Bm (s)
Am (s)
=
1
s²+1.4s+1
A equação de diophantina se torna:
A(s)Rp(s) + B-
(s)S(s) = Am(s)
s(s+a)*(s + r1) + b(s0s+s1) = (s²+ 2ζωs +ω²)(s+a0) = (𝑠² + 1.4𝑠 + 1)(s+1)
Equacionando os coeficientes de potências iguais obtivemos a seguinte equação:
a+r1 = 2ζω + a0
1+ r1 = 1.4 + 1
r1 = 1.4
ar1 + bs0 = ω² + 2ζωa0
r1 + s0 = 2.14

6. s0 = 2.4 – 1.4
s0 = 1
bs1 = ω²a0
s1 = 1
As equações acima são possíveis de resolver se a variável b ≠ 0. Além disso, temos
B+
= 1, B-
= b = 1, e B’m = ω²/b = 1, logo:
R(s) = B+
= 1
S(s) = s0s + s1 = s + 1
T(s) = B’m(s)A0(s) =
ω²
𝑏
(s+ a0) = s + 1
1+𝑎𝑚 1+𝑎𝑚 2
𝑏0+𝑏1
= Bmp(z) =
1−1.3205−0.496
0.10653+0.0902
= - 4.15
s0 =
𝑎𝑚 1−𝑎1
𝑏0
=
−1.3205+1.607
0.10653
= 2.6852
s1 =
𝑎𝑚 2−𝑎2
𝑏0
=
−0.4966+0.6065
0.10653
= 1.0321
EXEMPLO 3.4AUTOREGULADOR INDIRETO COM CANCELAMENTO DO
ZERO
Dado o sistema em tempo continuo utilizado no exemplo 3.1:
𝑦+𝑦 = u,
G(s) =
𝑏
𝑠(𝑠+𝑎)
Sua função discreta com período de amostragem h = 0.5 seg é
G(z) =
𝑏1𝑧+𝑏0
𝑧²+𝑎1𝑧+𝑎2
=
0.10653(𝑧+0.8467)
𝑧−1 (𝑧−0.6065)
Consideraremos o sinal de entrada ucéuma onda quadrada
O parâmetro da planta será mostrado a seguir:
b0 = 0.1065
b1 = 0.0902
a1 = -1.6065
a2 = 0.6065

7. com os parâmetros determinados no exemplo 3.1 temos
ωn = 1rad/s (freqüência natural)
ζ = 0.7 (amortecimento)
O desafio é sintetizar um controlador com 2 graus de liberdade cujo a função de
transferência desejado é
𝐵𝑚(𝑧)
𝐴𝑚 (𝑧)
=
0.1761 𝑧
𝑧²−1.3205𝑧−0.496
A partir dos dados de amortecimento e freqüência natural determinados pelo exemplo
podemos obter os pólos desejados da planta da seguinte maneira:
Poldes = 𝑒^(-ζωnh+jωn 1 − ζ ∗ ℎ)
-ζωnh+jωn 1 − ζ ∗ ℎ = -0.5+j0.2739
Poldes = 𝑒^(-0.5+j0.2739)
Através de manipulações matemáticas confirmaremos esses valores
am = z² - 1.3205z + 0.496
am1 = -1.3205
am2 = 0.496
bm= 0.1761z = b0
para resolver este exemplo, utilizaremos o algoritmo 3.2
PASSO 1: a partir de agora iremos implementar o método dos mínimos quadrados para
a auto regulação, os parâmetros iniciais são:
fator de esquecimento (λ) = 0.65
obs: este valor do fator de esquecimento foi definido pois os parâmetros do controlador
encontrados na simulação são os mesmos dos valores reais
P(0) =
100 0 0
0 100 0
0
0
0 0 1
0 0 0
0
1
___________________________________

8. θ(0) =
0 0 0
0 0 0
0
0
0.01 0.01 0.01
0.2 0.2 0.2
0.01
0.2
____________________________________
φ(0)=
0 0 0
0 0 0
0
0
0 0 0
0 0 0
0
0
𝑦(0) =
0
0
0
𝑦(0) =
0
0
0
𝑢(0) =
0
0
0
Cálculo do MQR
A saída do sistema é calculada da seguinte forma
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2);
desse modo podemos atualizar o φ, o erro e o ganho do estimador
φ (k-1)=[-y(k-1) -y(k-2) u(k-1) u(k-2)]'
e(k)=y(k)- φ(k-1)'* θ (k-1)
K=P* φ (k-1)/(λ + φ(k-1)'*P* φ (k-1))
Calculamos o novo vetor de estimação de parâmetros
Teta(k)=Teta(k-1)+K*e(k);
A partir desses dados se atualiza a matriz de covariância
P=(P-K* φ (k-1)'*P)/λ
A próxima etapa é armazenar os parâmetros atualizados
Teta(k) = [ a1atualizado a2atualizado b0atualizado b1atualizado]’
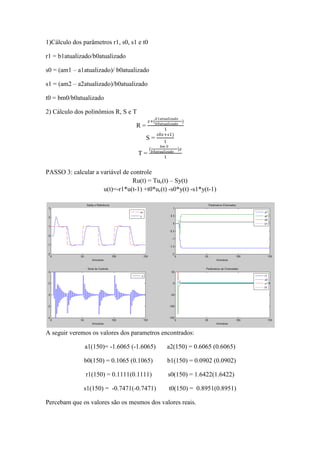
PASSO 2: aplicar o método de alocação de pólos e grau mínimo dado pelo algoritmo
3.1 onde os polinômios A e B são os estimadores obtidos no passo 1. Os polinômios R,S
e T do controlador então são obtidos:

9. 1)Cálculo dos parâmetros r1, s0, s1 e t0
r1 = b1atualizado/b0atualizado
s0 = (am1 – a1atualizado)/ b0atualizado
s1 = (am2 – a2atualizado)/b0atualizado
t0 = bm0/b0atualizado
2) Cálculo dos polinômios R, S e T
R =
𝑧+(
𝑏1𝑎𝑡𝑢𝑎𝑙𝑖𝑧𝑎𝑑𝑜
𝑏0𝑎𝑡𝑢𝑎𝑙𝑖𝑧𝑎𝑑𝑜
)
1
S =
𝑠0𝑧+𝑠1)
1
T =
(
𝑏𝑚 0
𝑏0𝑎𝑡𝑢𝑎𝑙𝑖𝑧𝑎𝑑𝑜
)𝑧
1
PASSO 3: calcular a variável de controle
Ru(t) = Tuc(t) – Sy(t)
u(t)=-r1*u(t-1) +t0*uc(t) -s0*y(t) -s1*y(t-1)
A seguir veremos os valores dos parametros encontrados:
a1(150)= -1.6065 (-1.6065) a2(150) = 0.6065 (0.6065)
b0(150) = 0.1065 (0.1065) b1(150) = 0.0902 (0.0902)
r1(150) = 0.1111(0.1111) s0(150) = 1.6422(1.6422)
s1(150) = -0.7471(-0.7471) t0(150) = 0.8951(0.8951)
Percebam que os valores são os mesmos dos valores reais.

10. EXEMPLO 3.5 AUTOREGULADOR INDIRETO SEM CANCELAMENTO DO
ZERO
Dado o sistema em tempo continuo utilizado no exemplo 3.1:
𝑦+𝑦 = u,
G(s) =
𝑏
𝑠(𝑠+𝑎)
Sua função discreta com período de amostragem h = 0.5 seg é
G(z) =
𝑏1𝑧+𝑏0
𝑧²+𝑎1𝑧+𝑎2
=
0.10653(𝑧+0.8467)
𝑧−1 (𝑧−0.6065)
Consideraremos o sinal de entrada ucé uma onda quadrada
O parâmetro da planta será mostrado a seguir:
b0 = 0.1065
b1 = 0.0902
a1 = -1.6065
a2 = 0.6065
com os parâmetros determinados no exemplo 3.1 temos
ωn = 1rad/s (freqüência natural)
ζ = 0.7 (amortecimento)
O desafio é sintetizar um controlador com 2 graus de liberdade cujo a função de
transferência desejado é
𝑏𝑚 0𝑧+𝑏𝑚 1
𝑧²+𝑎𝑚 1𝑧+𝑎𝑚 2
=
𝐵𝑚(𝑧)
𝐴𝑚 (𝑧)
=
𝛽(𝑧+0.8467)
𝑧²−1.3205𝑧−0.496
=
0.1761 𝑧
𝑧²−1.3205 𝑧−0.496
Com
β =
𝐴𝑚 (1)
𝐵𝑚(1)
=
1+𝑎𝑚 1+𝑎𝑚 2
𝑏0+𝑏1
= Bmp(z) = 0.8951
A partir dos dados de amortecimento e freqüência natural determinados pelo exemplo
podemos obter os pólos desejados da planta da seguinte maneira:
Poldes = 𝑒^(-ζωnh+jωn 1 − ζ ∗ ℎ)
-ζωnh+jωn 1 − ζ ∗ ℎ = -0.5+j0.2739

11. Poldes = 𝑒^(-0.5+j0.2739)
Através de manipulações matemáticas confirmaremos esses valores
am = z² - 1.3205z + 0.496
am1 = -1.3205
am2 = 0.496
bm= 0.1761z = b0
desde que os parâmetros amostrados da planta possam depender tanto dos parâmetros
contínuos conhecidos e desconhecidos, procederemos como se todos os parâmetros
fossem desconhecidos. Precisamos de um modelo de regressão linear para os
parâmetros da planta
θ = ( b0 b1 a1 a2 )T
φ(t) = ( u(t − 1) u(t − 2) −y(t − 1) −y(t − 2) )
o PASSO 1 utilizado aqui é o mesmo utilizado no exemplo 3.4, logo omitiremos
Antes de mais nada, precisamos desenvolver um controlador sem o cancelamento do processo
zero considerando B+
= 1. Usando a condição de causalidade degAc≥ 2degA-1 = 3, sendo que o
grau de A = 2. O grau de R deve ser portanto de grau 1. O grau mínimo é obtido pela escolha
dos menores graus possíveis no desenvolvimento do polinômio, então obtemos degAc = 3 e
degR = degS = 1. A equação de Diophantina para o problema é
(z2
+ a1z+ a2)(z+ r1) + (b0z+ b1)(s0z+ s1) = (z2
+ am1z+ am2)(z + ao1)
A identificação dos coeficientes de potências iguais para Z é:
z2
: a1+ r1+ b0s0= am1+ ao1
z1
: a2+ a1r1+ b1s0+ b0s1= am1ao1+ am2
z0
: a2r1+ b1s1= am2ao1
PASSO 2: a solução da equação linear é
r1 =
𝑎0𝑎𝑚 2𝑏²0+ 𝑎2−𝑎𝑚 2−𝑎0𝑎𝑚 1 𝑏0𝑏1+ 𝑎0+𝑎𝑚 1−𝑎1 ∗𝑏²1
𝑏21−𝑎1𝑏0𝑏1+𝑎2𝑏20
s0 =
𝑎𝑚 1+𝑎0−(𝑟1+𝑎1)
𝑏0
s1 =
𝑎0𝑎𝑚 2−𝑎2𝑟1
𝑏1
PASSO 3: encontrados os coeficientes, é possível determinar os polinômios da equação
diophantina:
R(z) = z + r1 (R é mônico de primeira ordem)

12. S(z) = s0z + s1 (S é de primeira ordem)
Como: grau{A0(z)} = 0 e obtemos A0(z) = 1.
O parâmetro a0 teve seu valor igual a 1, sendo assim temos:
T = βA0(z) = β(z + a0)
A seguir veremos a simulação deste exemplo:
Os valores dos parametros encontrados são:
a1(150)= -1.6065 (-1.6065) a2(150) = 0.6065 (0.6065)
b0(150) = 0.1065 (0.1065) b1(150) = 0.0902 (0.0902)
r1(150) = 0.1111(0.1111) s0(150) = 1.6422(1.6422)
s1(150) = -0.7471(-0.7471) t0(150) = 0.8951(0.8951)
Os valores dos parâmetros são os mesmos dos valores reais.
Obs: nesta simulação foi utilizado um fator de esquecimento λ = 0.65
EXEMPLO 3.7 AUTOREGULADOR DIRETO COM d0 = 1
Consideremos o sistema no exemplo 3.1. Desde que degA = 2 e degB = 1, temos
degAm = 2 e degA0 = 1, e vamos escolher Bm = qAm(1). Usando a equação 3.29 no
algoritmo 3.3 então temos T = qAm(1). A estrutura do controlador é dada por
degR=degS = degA-1 = 1. O modelo dado pela equação 3.27 portanto se torna:
y(t) = r0uf(t-1) + r1uf(t-2) + s0yf(t-1) + s1yf(t-2)

13. onde
uf(t) +am1uf(t-1) + am1uf(t-2) = u(t)
yf(t) + am1yf(t-1) + am1yf(t-2) = y(t)
isso é importante agora obter um auto-regulador direto pela aplicação do algoritmo 3.3.
Os modelos do parâmetros dados pela equação (3.30) são portanto estimados, e o sinal
de controle é computado da seguinte maneira:
𝑟0u(t) +𝑟1u(t-1) = 𝑡0uc(t) - 𝑠0y(t) - 𝑠1y(t-1)
Onde 𝑟0,𝑟1, 𝑠0, e 𝑠1são os estimadores obtidos e 𝑡0 é dado pela equação 3.29, que é
𝑡0= 1 + am1 + am2
Perceba que o estimador de r0 deve ser diferente de zero para o controlador ser causal.
A figura acima onde compara o sinal de entrada e de saída na simulação do algoritmo
direto e a figura seguinte mostra os parâmetros estimados. O transitório inicial depende
fortemente das condições iniciais. Em t = 150 os parâmetros do controlador são:

14. r1/r0(150) = 0.8467(0.8467) s0/r0(150) = 2.6852(2.6852)
s1/r0(150) = -1.0321(-1.0321) t0/r0(150) = 1.6531(1.6531)
neste exemplo foi utilizado um fator de esquecimento λ = 0.65
Os parâmetros do controlador são divididos por 𝑟0 para fazer uma comparação direta
com os exemplos 3.1 e 3.3. os valores corretos são dados em parênteses. O limite da lei
de controle é o mesmo em ambos os casos, existe uma “oscilação” no sinal de controle
por causa do cancelamento do processo zero.
Num caso prático o tempo de atraso e a ordem do processo que gostaríamos de controlar
são desconhecidos. Portanto é natural considerar essas variáveis como parâmetros
desenvolvidos que são escolhidos pelo usuário. O parâmetro d0 é de importância
particular para um algoritmo direto. O próximo exemplo mostrará que a “oscilação”
pode ser evitado simplesmente pelo aumento do valor de d0.
EXEMPLO 3.8 AUTOREGULADOR DIRETO COM d0 = 2
Na derivação do algoritmo direto o parâmetro d0 foi o pólo em excesso da planta.
Assuma por um momento que não sabemos o valor de d0 e isso trataremos como um
parâmetro desenvolvido no lugar. A figura abaixo mostra uma simulação do algoritmo
direto usado no exemplo 3.7 mas com d0 = 2 no lugar de d0 =1.
Todos os outros parâmetros são os mesmos. Perceba que o comportamento do sistema é
um pouco razoável sem qualquer “oscilação” no sinal de controle. A figura abaixo
mostra os parâmetros estimados. Os estimadores obtidos no tempo t = 100
correspondem aos parâmetros do controlador

15. r1/r0(150) = -0.1643(0.8467) s0/r0(150) = 1.21(2.6852)
s1/r0(150) = -0.5987(-1.0321) t0/r0(150) = 0.6214(1.6531)
neste exemplo foi utilizado um fator de esquecimento λ = 1
Nos encontramos um resultado interessante e surpreendente do cancelamento do
processo zero que pode ser evitado pelo aumento do parâmetro d0.
EXEMPLO 3.9 EFEITOS DO DISTURBIO NA LEITURA
Consideremos o sistema no exemplo 3.5 que é, um regulador de auto sintonização
indireta sem cancelamento de zero. Será feita uma simulação que é idêntica para o
mostrado no exemplo 3.6 exceto que o distúrbio na leitura será de v(t) = 0.5 para t ≤ 40.
O fator de esquecimento igual a 0.98 tem foi introduzido; por outro lado as condições
são as mesmas para a escolhida no exemplo 3.5. o comportamento do sistema é
mostrado abaixo, comparando com outros exemplos percebemos que o efeito do
distúrbio na leitura pode ser desastroso. Isso segue da discussão no exemplo 3.5 que o
valor correto de regime permanente vai sempre ser alcançado ao passo que os steps são
suficientes grandes.

16. Perceba que a resposta é grandemente assimétrica. O motivo para isso é que os
parâmetros mudam rapidamente quando o sinal do controlador muda; rápidas mudanças
dos estimadores para o sinal de comando indica que a estrutura do modelo que não é
correta. Os parâmetros dos estimadores também mudam significativamente no passo do
distúrbio da leitura. Quando o sinal de comando é constante, os parâmetros aparecem se
acomodar num valor constante são próximos dos verdadeiros parâmetros.
EXEMPLO 3.10 DISTURBIO NA LEITURA: CONTROLADORES E
ESTIMADORES MODIFICADOS
Mostraremos agora as dificuldades encontradas no exemplo 3.9 podem ser evitadas pela
modificação dos estimadores e controladores. Primeiro introduzimos um controlador
que tem uma ação integral pela aplicação do desenvolvimento do projeto que foi
mostrado abaixo:

17. Para fazer isso, consideraremos o mesmo sistema como no exemplo 3.5 onde o
controlador foi definido como:
R
0
= q + r1S
0
= s0q + s1
opolinômio característico em malha fechada Ac tem grau 3. Para obter um controlador
com ação integral, a ordem em malha fechada do sistema é aumentada pela introdução
de um extra polo em malha fechada em z = -x0 = 0. Isso segue então da equação 3.41 do
livro que
𝑦0 = −
1 − 𝑟1
𝑏0 + 𝑏1
Desde que X = z e Y = y0, as equações 3.39 agora fornecem:
R = z(z+r1) + y0(b0z + b1) = (z -1)(z-b1y0)
S = (s0 − y0)z2
+ (s1 − a1y0)z− a2y0
Os estimadores são baseados no modelo 3.42 do livro com Ad = z-1 para reduzir os
efeitos dos distúrbios. Os distúrbios na leitura reduzem rapidamente pois a ação integral
do controlador vai diminuir com a magnitude correspondente para o distúrbio curto
depois de t = 40. Os parâmetros estimados são mostrado abaixo, cujo indica vantagem
no uso do estimador modificado. Perceba em particular que existem uma pequena
mudança nos estimadores quando o distúrbio na leitura acontece.

18. PROBLEMAS
3.1 uma amostra de um modelo de um processo em tempo continuo com h = 1 a
seguinte função pulso de transferência é obtida
𝐻(𝑧) =
𝑧 + 1.2
𝑧² − 𝑧 + 0.25
A especificação do projeto de estado que os pólos em malha fechada em tempo discreto
deveriam corresponder para a seguinte característica polinomial:
S² + 2s + 1
(a)projete um regulador auto ajustável indireto de ordem mínima em tempo discreto. O
controlador deve ter uma ação integral e dar um sistema em malha fechada tendo um
ganho unitário em regime permanente. Determine a equação de diophantina para
resolver o problema do projeto.
RESPOSTA
Especificações do projeto: o sistema em malha fechada teria um pólo que
corresponderia a seguinte característica polinomial em tempo continuo
S² + 2s + 1 = (s+1)²
Isso corresponde a

19. Am(z) = z²+am1z + am2
Com
𝑎𝑚1 = − 𝑒−1
+ 𝑒−1
= −2𝑒−1
𝑎𝑚2 = 𝑒−2
A escolha de Bm seria então:
𝐵𝑚(1)
𝐴𝑚 (1)
= 1
A condição de integrador dá
R = R(z-1)
A partir disso temos a seguinte condições:
(1) BT = BmA0
(2) AR + BS = AmA0
Como B é instável devemos ter Bm = BB’m. isso faz (1) ↔ BT = BB’mA0 ↔ T = BmA0.
Escolhido Bm temos que:
𝐵(1)𝐵𝑚(1)
𝐴(1)
= 1 → B’m(1) =
𝐴(1)
𝐵(1)
O jeito mais simples de escolher é
B’m = b’m =
𝐴(1)
𝐵(1)
=
0.25
2.2
Alem do mais, temos
(z2
+ a1z + a2)(z−1)(z + r) + (b0z + b1)(s0z2
+ s1z + s2)= (z2
+ am1z + am2)(z2
+ ao1z + ao2)
Com a1 = -1, a2 = 0.25 e a01 e a02 escolhidos de um jeito que A0 é estável.
Equacionando os coeficientes temos:
r −1 + a1 + b0s0 = ao1 + am1
−r + a1(r−1) + a2 + b0s1 + b1s0 = ao2 + am1ao1 + am2
−ar + a2(r−1) + b0s2 + b1s1 = am1ao2 + am2ao1
−a2r + b1s2 = am2ao2
Agora escolhemos os estimadores
θ = ( b0 b1 a1 a2 )T
pela equação 3.22 do livro
(b) sugira um projeto que inclua uma estimação direta dos parâmetros do controlador.
Diga porque uma regulação auto ajustável direta bem feita é mais difícil para projetar
para esse projeto do que um regulador auto ajustável indireto.

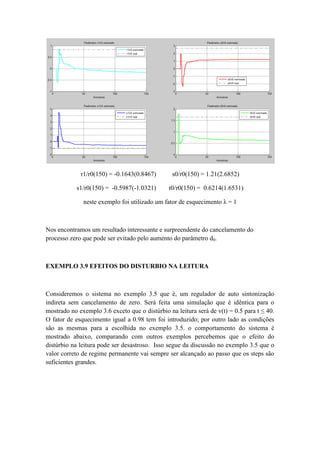
20. RESPOSTA
Como H(z) não é fase mínima cancelaremos B-
= B entre 𝑅 e 𝑆. Um STR indireto é
dado pela equação 3.24
A0Amym = 𝑅u + 𝑆y
Com
𝑅 = B-
R, 𝑆 = B-
S, T = B’mA0.
Além do mais temos
A0Amym = A0Bmuc = A0BB’muc = BTuc = 𝑇uc
y = 𝑅
1
𝐴0𝐴𝑚
u + 𝑆
1
𝐴0𝐴𝑚
y
ym = 𝑇
1
𝐴0𝐴𝑚
uc
Ɛ = y – ym = 𝑅uf + 𝑆yf - 𝑇ucf
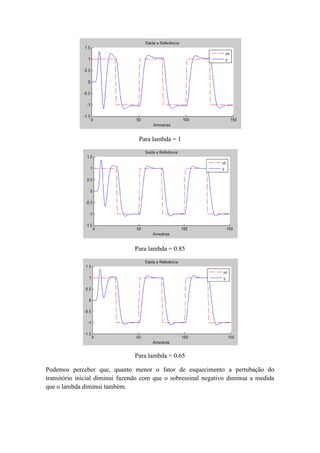
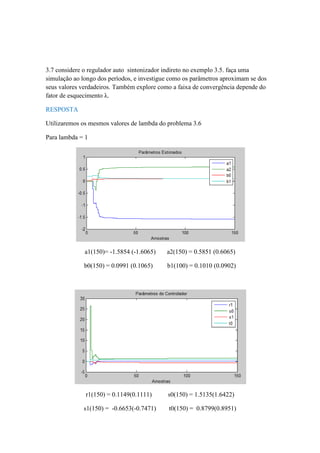
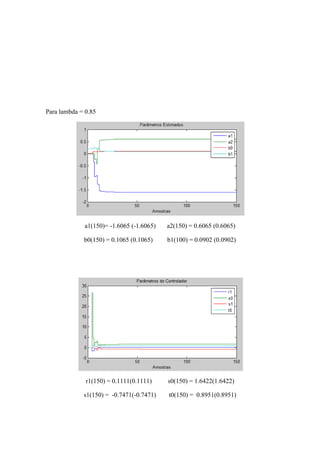
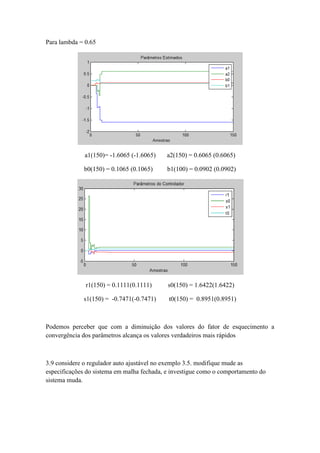
3.6 Considere a simulação do regulador de auto sintonização indireta usado no exemplo
3.5. investigue como o comportamento do transiente do algoritmo depende do valor
inicial de teta, da matriz de covariância e o fator de esquecimento.
RESPOSTA
Para resolução deste problema usaremos 3 valores distintos para cada variável
mencionada no enunciado, os valores são:
λ1= 1
λ 2= 0.85
λ 3 = 0.65
P1 = diag([200 200 2 2])
P2 = diag([100 100 1 1])
P3 = diag([50 50 0.5 0.5])
θ1 = [0 0 0.01 0.2]T
θ 2 = [0 0 0.1 2]T
θ 3 = [0 0 1 20]T
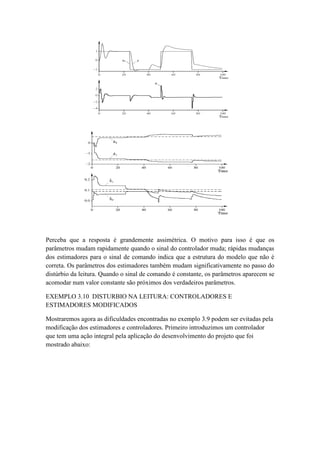
vamos agora analisar a influência de lambda

21. Para lambda = 1
Para lambda = 0.85
Para lambda = 0.65
Podemos perceber que, quanto menor o fator de esquecimento a pertubação do
transitório inicial diminui fazendo com que o sobressinal negativo diminua a medida
que o lambda diminui também.

22. vamos agora analisar a influência da matriz de covariância (considerando lambda = 1).
Para covariancia = diag([200 200 2 2])
Para covariância = diag([100 100 1 1])
Para covariância = diag([50 50 0.5 0.5])
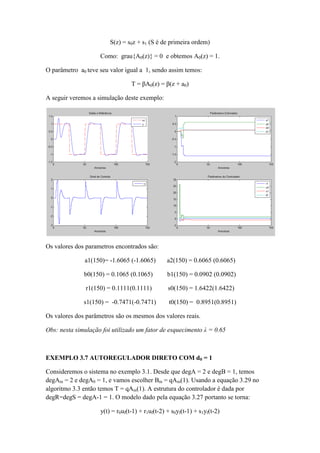
Percebemos que quanto menor o valor o valor inicial de teta, o sistema passar a ter uma
“dificuldade em acompanhar” inicialmente o valor de referência aumentando o valor do
erro de regime permanente.

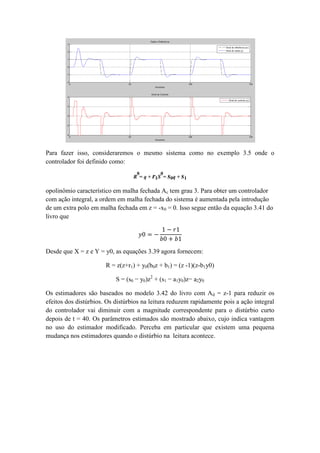
23. vamos agora analisar a influência de teta (considerando lambda = 1 e
cov = [100 100 1 1] ).
.
Para teta = [0 0 0.01 0.2]T
Para teta = [0 0 0.1 2]T
Para teta = [0 0 1 20]T
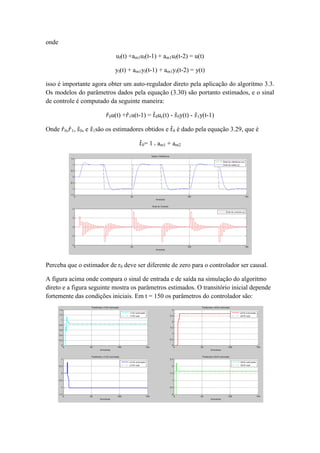
O valor inicial de teta deve ser o menor possível, pois a mínima variação pode causar a
instabilidade no sistema.

24. 3.7 considere o regulador auto sintonizador indireto no exemplo 3.5. faça uma
simulação ao longo dos períodos, e investigue como os parâmetros aproximam se dos
seus valores verdadeiros. Também explore como a faixa de convergência depende do
fator de esquecimento λ.
RESPOSTA
Utilizaremos os mesmos valores de lambda do problema 3.6
Para lambda = 1
a1(150)= -1.5854 (-1.6065) a2(150) = 0.5851 (0.6065)
b0(150) = 0.0991 (0.1065) b1(100) = 0.1010 (0.0902)
r1(150) = 0.1149(0.1111) s0(150) = 1.5135(1.6422)
s1(150) = -0.6653(-0.7471) t0(150) = 0.8799(0.8951)

25. Para lambda = 0.85
a1(150)= -1.6065 (-1.6065) a2(150) = 0.6065 (0.6065)
b0(150) = 0.1065 (0.1065) b1(100) = 0.0902 (0.0902)
r1(150) = 0.1111(0.1111) s0(150) = 1.6422(1.6422)
s1(150) = -0.7471(-0.7471) t0(150) = 0.8951(0.8951)

26. Para lambda = 0.65
a1(150)= -1.6065 (-1.6065) a2(150) = 0.6065 (0.6065)
b0(150) = 0.1065 (0.1065) b1(100) = 0.0902 (0.0902)
r1(150) = 0.1111(0.1111) s0(150) = 1.6422(1.6422)
s1(150) = -0.7471(-0.7471) t0(150) = 0.8951(0.8951)
Podemos perceber que com a diminuição dos valores do fator de esquecimento a
convergência dos parâmetros alcança os valores verdadeiros mais rápidos
3.9 considere o regulador auto ajustável no exemplo 3.5. modifique mude as
especificações do sistema em malha fechada, e investigue como o comportamento do
sistema muda.

27. RESPOSTA
Foi considerado a seguinte função em malha fechada:
y(t)= -a1y(t-2)-a2y(t-3)+b0u(t-1)+b1u(t-2)
foi adicionado um delay a mais nas variáveis de saída do sistema (destacado de
vermelho) os parâmetros da entrada não foi alterado
Podemos analisar que na prática se a planta por algum motivo falhasse em fornecer a
informação do sistema isso poderia acarretar em sérios problemas, pois pode-se
observar que um simples delay na saída da planta já é o suficiente para levar a
instabilidade do sistema.
3.11 aplique o regulador auto ajustável indireto do exemplo 3.5 para o processo com a
função de transferência
𝐺(𝑠) =
1
(𝑠 + 1)²
Estude e explique o comportamento do erro quando o sinal de referência é uma onda
quadrada.
RESPOSTA
Primeiro veremos como é o comportamento do sistema para a seguinte função de
transferência :
𝐺(𝑠) =
1
𝑠² + 2𝑠

28. Agora veremos o comportamento do sistema para a função de transferência sugerida
pelo enunciado:
Comparando as duas situações, podemos ver que o deslocamento do pólo no eixo zero
para a esquerda tem um efeito percebível na saída do sistema:
Nos momentos iniciais o sobressinal é reduzido consideravelmente em relação a função
de transferência original, isso se deve ao fato do pólo ter sido deslocado do eixo zero
para a esquerda, por outro lado, repare que o sinal de controle mantém um “esforço”
maior para tentar minimizar o erro, a partir de t =25 o erro em regime permanente é
igual em ambos os casos.

29. ANEXOS
/////////////////EXEMPLO 3.4///////////////////////////////
%% STR indireto usando MQR e MDPP
% Astrom & Wittenmark, Exemplo 3.4, p.104
% Prof. André Ferreira - 29/01/2014
% MODIFICADO POR PEDRO JUNIOR
clear all
close all
clc
%% Definição da planta
planta=tf(1,[1 1 0]); % Planta analógica
Ts=0.5; % Intervalo de amostragem
planta_discretizada=c2d(planta,Ts); % Planta discretizada
% Parâmetros da planta
[numd,dend]=tfdata(planta_discretizada,'v');
b0=numd(2);
b1=numd(3);
a1=dend(2);
a2=dend(3);
%% Sistema em MF desejado
csi=0.7;
freq_nat=1;
% Pólos discretos desejados
pol_des=exp(-csi*freq_nat*Ts + j*freq_nat*sqrt(1-csi^2)*Ts);
Pol_des=[pol_des conj(pol_des)];
% FT desejada em MF
Am=poly([pol_des conj(pol_des)]);
Bm=[polyval(Am,1) 0]; % Escolhido para ter ganho DC unitário
func_desej_disc=tf(Bm,Am,Ts);
% Parâmetros da planta desejada em MF
[nummd,denmd]=tfdata(func_desej_disc,'v');
bm0=nummd(2);
am1=denmd(2);
am2=denmd(3);
%% Vetor de Entrada - Onda Quadrada (u)
uc = [];
neg=-1*ones(1,25);
pos=ones(1,25);
for i = 1:3
uc = [uc pos neg];
end
%% Condições iniciais necessários para o MQR
N = length(uc); % Número de realizações (medidas)
lambda = 0.65; %pulo do gato - valor escolhido por tentativa e erro

30. covP0 = diag([100 100 1 1]); % Inicializar a matriz de covariância
*****
Theta0 = [0 0 0.01 0.2]'; % Inicializar o vetor de parâmetros Teta
estimado *****
fi0=[0 0 0 0]';
yest=[0 0 0]';
diagP=diag(covP0)';
Theta=[Theta0 Theta0 Theta0];
fi=[fi0 fi0 fi0];
diagP=[diagP; diagP; diagP];
P=covP0;
cont=0*Theta;
y=0*yest;
u=0*yest;
erro=0*yest;
for k = 4:N
%% MQR
% ----- Calcula a saída atual
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2); % Saída da
planta
% ----- Atualiza Fi
fi(:,k-1)=[-y(k-1) -y(k-2) u(k-1) u(k-2)]';
% ----- Calcula o erro de estimação
erro(k)=y(k)-fi(:,k-1)'*Theta(:,k-1);
% ----- Calcula o vetor de ganhos
K=P*fi(:,k-1)/(lambda+fi(:,k-1)'*P*fi(:,k-1));
% ----- Calcula o novo vetor de estimação de parâmetros
Theta(:,k)=Theta(:,k-1)+K*erro(k);
% ----- Atualiza a matriz de covariância
P=(P-K*fi(:,k-1)'*P)/lambda;
diagP=[diagP; diag(P)'];
% ----- Armazena parâmetros
a1est = Theta(1,k);
a2est = Theta(2,k);
b0est = Theta(3,k);
b1est = Theta(4,k);
%% PASSO 2 - valores dos polinômios R, S e T
r1 = b1est/b0est;
s0 = (am1-a1est)/b0est;
s1 = (am2-a2est)/b0est;
t0 = bm0/b0est;
cont(:,k)=[r1 s0 s1 t0]';
%Polinômios R, S e T:
R= tf([1 b1est/b0est],1,0.5); %tf([1 r1],1,0.5);
S=tf([s0 s1],1,0.5);
%t0= beta*1;
%t1= beta*a0;
T= tf([(bm0/b0est) 0],1,0.5); %tf([t0 t1],1,0.5);
cont(:,k)=[r1 s0 s1 t0]';

31. %% PASSO 3 - cálculo da lei de controle
u(k)=-r1*u(k-1) +t0*uc(k) -s0*y(k) -s1*y(k-1); % Sinal de controle
% Limite do sinal de controle
if u(k)>=4,
u(k)=4;
elseif u(k)<=-4,
u(k)=-4;
end
end
subplot(221)
hold on
plot(uc,'r--')
plot(y,'b')
legend('uc','y')
xlabel('Amostras')
title('Saída e Referência');
subplot(223)
stairs(u,'b')
legend('u')
xlabel('Amostras')
title('Sinal de Controle');
subplot(224)
stairs(cont')
legend('r1','s0','s1','t0')
xlabel('Amostras')
title('Parâmetros do Controlador');
subplot(222)
stairs(Theta')
legend('a1','a2','b0','b1')
xlabel('Amostras')
title('Parâmetros Estimados');
hold off
///////////////////////////////////////////////////////////
////////EXEMPLO 3.5////////////////////////////////////////
%% STR indireto usando MQR e MDPP
% Astrom & Wittenmark, Exemplo 3.4, p.104
% Prof. André Ferreira - 29/01/2014
%MODIFICADO POR PEDRO JUNIOR
clear all
close all
clc
%% Definição da planta
g=tf(1,[1 1 0]); % Planta analógica
Ts=0.5; % Intervalo de amostragem
gd=c2d(g,Ts); % Planta discretizada

32. % Parâmetros da planta
[numd,dend]=tfdata(gd,'v');
b0=numd(2);
b1=numd(3);
a1=dend(2);
a2=dend(3);
%% Sistema em MF desejado
csi=0.7;
Wn=1;
% Pólos discretos desejados
pdes=exp(-csi*Wn*Ts + j*Wn*sqrt(1-csi^2)*Ts);
Pdes=[pdes conj(pdes)];
% FT desejada em MF
Am=poly([pdes conj(pdes)]);
Bm=[polyval(Am,1) 0]; % Escolhido para ter ganho DC unitário
gmd=tf(Bm,Am,Ts);
% Parâmetros da planta desejada em MF
[nummd,denmd]=tfdata(gmd,'v');
bm0=nummd(2);
am1=denmd(2);
am2=denmd(3);
%Polinômio A0:
a0=0; %Este parâmetro é sugerido no próprio livro
A0=tf([1 a0],[1],0.5);
%% Vetor de Entrada - Onda Quadrada (u)
uc = [];
neg=-1*ones(1,25);
pos=ones(1,25);
for i = 1:3
uc = [uc pos neg];
end
%% Condições iniciais necessários para o MQR
N = length(uc); % Número de realizações (medidas)
lambda = 0.65; %pulo do gato (^-^)
P0 = diag([100 100 1 1]); % Inicializar a matriz de covariância *****
Teta0 = [0 0 0.01 0.2]'; % Inicializar o vetor de parâmetros Teta
estimado *****
fi0=[0 0 0 0]';
yest=[0 0 0]';
diagP=diag(P0)';
Teta=[Teta0 Teta0 Teta0];
fi=[fi0 fi0 fi0];
diagP=[diagP; diagP; diagP];
P=P0;
cont=0*Teta;

33. y=0*yest;
u=0*yest;
erro=0*yest;
for k = 4:N
%% MQR
% ----- Calcula a saída atual
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2); % Saída da
planta
% ----- Atualiza Fi
fi(:,k-1)=[-y(k-1) -y(k-2) u(k-1) u(k-2)]';
% ----- Calcula o erro de estimação
erro(k)=y(k)-fi(:,k-1)'*Teta(:,k-1);
% ----- Calcula o vetor de ganhos
K=P*fi(:,k-1)/(lambda+fi(:,k-1)'*P*fi(:,k-1));
% ----- Calcula o novo vetor de estimação de parâmetros
Teta(:,k)=Teta(:,k-1)+K*erro(k);
% ----- Atualiza a matriz de covariância
P=(P-K*fi(:,k-1)'*P)/lambda;
diagP=[diagP; diag(P)'];
% ----- Armazena parâmetros
a1est = Teta(1,k);
a2est = Teta(2,k);
b0est = Teta(3,k);
b1est = Teta(4,k);
%Operador de Transferência:
%am1=Amq(2);
%am2=Amq(3);
beta=((1+am1+am2)/(b0est+b1est));
bm0=beta*b0est;
bm1=beta*b1est;
Hmq=tf([bm0 bm1],[1 am1 am2],0.5);
%% PASSO 2 - valores dos polinômios R, S e T
% r1 = b1est/b0est;
% s0 = (am1-a1est)/b0est;
% s1 = (am2-a2est)/b0est;
% t0 = bm0/b0est;
% cont(:,k)=[r1 s0 s1 t0]';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Coeficientes r1, s1 e s0:
r1=((a0*am2*(b0est*b0est))+((a2est-am2-a0*am1)*(b1est*b0))+((a0+am1-
a1est)*(b1est*b1est)))/((b1est*b1est)-
(b1est*b0est*a1est)+(a2est*(b0est*b0est)));
s1=((a0*am2)-(a2est*r1))/(b1est);
s0=((am1+a0)-(r1+a1est))/(b0est);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Polinômios R, S e T:
R=tf([1 r1],1,0.5);
S=tf([s0 s1],1,0.5);
t0= beta*1;
t1= beta*a0;
T=tf([t0 t1],1,0.5);

34. cont(:,k)=[r1 s0 s1 t0]';
% %Polinômios R, S e T:
%R= tf([1 b1/b0],1,0.5); %tf([1 r1],1,0.5);
%S=tf([s0 s1],1,0.5);
%t0= beta*1;
%t1= beta*a0;
%T= tf([(bm0/b0) 0],1,0.5); %tf([t0 t1],1,0.5);
%% PASSO 3 - cálculo da lei de controle
u(k)=-r1*u(k-1) +t0*uc(k) -s0*y(k) -s1*y(k-1); % Sinal de controle
% Limite do sinal de controle
if u(k)>=4,
u(k)=4;
elseif u(k)<=-4,
u(k)=-4;
end
end
subplot(221)
hold on
plot(uc,'r--')
plot(y,'b')
legend('uc','y')
xlabel('Amostras')
title('Saída e Referência');
subplot(223)
stairs(u,'b')
legend('u')
xlabel('Amostras')
title('Sinal de Controle');
subplot(224)
stairs(cont')
legend('r1','s0','s1','t0')
xlabel('Amostras')
title('Parâmetros do Controlador');
subplot(222)
stairs(Teta')
legend('a1','a2','b0','b1')
xlabel('Amostras')
title('Parâmetros Estimados');
hold off
///////////////////////////////////////////////////////////
///////////EXEMPLO 3.7 & 3.8//////////////////////////////
%Aluno:PEDRO JUNIOR
%Exemplo 3.7 E 3.8
clear all
close all
clc

35. %% Função de transferencia
G=tf(1,[1 1 0]);
%Tempo de amostragem
h=0.5;
%Função de transferencia discretizada
Gd=c2d(G,h);
%Parametros da planta
[Bd,Ad]=tfdata(Gd,'v');
b0=Bd(2);
b1=Bd(3);
a1=Ad(2);
a2=Ad(3);
%% Sistema desejado em malha fechada
%Dados para o sistema em malha fechada
csi=0.7;
Wn=1;
% Pólos discretos desejados
pdes=exp(-csi*Wn*h + j*Wn*sqrt(1-csi^2)*h);
P=[pdes conj(pdes)];
% FT desejada em MF
Am=poly([pdes conj(pdes)]);
Bm=[polyval(Am,1) 0];
Gmd=tf(Bm,Am,h);
% Parâmetros da planta desejada em malha fechada
[Bmd,Amd]=tfdata(Gmd,'v');
bm0=Bmd(2);
am1=Amd(2);
am2=Amd(3);
%% Vetor de Entrada para a Onda Quadrada (uc);
N=input(' Entre com o numero de Interações?:');
%% Sinal de entrada Onda Quadrada;
j=0;
while j<N
for j=j+1:j+25
uc(j)=1;
end
for j=j+1:j+25
uc(j)=-1;
end
end
%% Condições iniciais necessários para o MQR
N = length(uc); % Número de realizações (medidas)
lambda = 1;
P0 = 100*eye(4); % Inicializar a matriz de covariância *****
Teta0 = [0.1 0 0 0]'; % Inicializar o vetor de parâmetros Teta
estimado *****
fi0=[0 0 0 0]';

36. yest=[0 0 0]';
diagP=diag(P0)';
Teta=[Teta0 Teta0 Teta0];
fi=[fi0 fi0 fi0];
diagP=[diagP; diagP; diagP];
P=P0;
cont=0*Teta;
y=0*yest;
u=0*yest;
yf=0*yest;
uf=0*yest;
erro=0*yest;
%d0=1; % Atraso do sistema exemplo 3.7
d0=2; % Atraso do sistema exemplo 3.8
for k = 4:N
%% MQR
% ----- Calcula a saída atual
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2); % Saída da
planta
% ----- Atualiza Fi
fi(:,k-d0)=[uf(k-d0) uf(k-d0-1) yf(k-d0) yf(k-d0-1)]';
% ----- Calcula o erro de estimação
erro(k)=y(k)-fi(:,k-d0)'*Teta(:,k-1);
% ----- Calcula o vetor de ganhos
K=P*fi(:,k-d0)/(lambda+fi(:,k-d0)'*P*fi(:,k-d0));
% ----- Calcula o novo vetor de estimação de parâmetros
Teta(:,k)=Teta(:,k-1)+K*erro(k);
% ----- Atualiza a matriz de covariância
P=(P-K*fi(:,k-d0)'*P)/lambda;
diagP=[diagP; diag(P)'];
% ----- Armazena parâmetros
r0 = Teta(1,k);
r1 = Teta(2,k);
s0 = Teta(3,k);
s1 = Teta(4,k);
t0 = 1 + am1 + am2; % constante
%% PASSO 2 - Guarda parâmetros normalizados por ro
cont(:,k)=[r1/r0 s0/r0 s1/r0 t0/r0];
%% PASSO 3 - cálculo da lei de controle e da entrada e saída filtradas
u(k)=(t0*uc(k)-s0*y(k)-s1*y(k-1)-r1*u(k-1))/r0; % Sinal de
controle
uf(k) = u(k) - am1*uf(k-1) - am2*uf(k-2);
yf(k) = y(k) - am1*yf(k-1) - am2*yf(k-2);
% Limite do sinal de controle
if u(k)>=4,
u(k)=4;

37. elseif u(k)<=-4,
u(k)=-4;
end
end
%% Sinais de Entrada e Saida do Processo;
figure(1)
subplot(211)
grid on
hold on
plot(uc,'k--')
%Subplot(312)
plot(y,'b')
legend('Sinal de referência (uc)','Sinal de saída (y)')
xlabel('Amostras')
title('Saída e Referência');
%xlim([0 100])
%% Sinal de Controle;
subplot(212)
stairs(u,'r')
grid on
legend('Sinal de controle (u)')
xlabel('Amostras')
title('Sinal de Controle');
%xlim([0 100])
%% Parâmetros a1 e a2 do Processo real e estimados;
figure(2)
subplot(221)
hold on
grid on
stairs(cont(1,:),'c','LineWidth',2)
r1=0.8467*ones(1,N);
plot(r1,'k-.')
legend('r1/r0 estimado','r1/r0 real')
xlabel('Amostras')
title('Parâmetro r1/r0 estimado');
subplot(222)
hold on
grid on
stairs(cont(2,:),'r','LineWidth',2)
a2=2.6852*ones(1,N);
plot(a2,'k-.')
legend('s0/r0 estimado','s0/r0 real')
xlabel('Amostras')
title('Parâmetro s0/r0 estimado');
subplot(223)
hold on
grid on
stairs(cont(3,:),'b','LineWidth',2)
a3=-1.0321*ones(1,N);
plot(a3,'k-.')
legend('s1/r0 estimado','s1/r0 real')
xlabel('Amostras')
title('Parâmetro s1/r0 estimado');
subplot(224)
hold on
grid on
stairs(cont(4,:),'g','LineWidth',2)
a4=1.6531*ones(1,N);

38. %grid on
plot(a4,'k-.')
legend('t0/r0 estimado','t0/r0 real')
xlabel('Amostras')
title('Parâmetro t0/r0 estimado');
//////////////////////////////////////////////////////////////////////
//////////////////////EXEMPLO 3.10////////////////////////////////////
%Aluno:PEDRO JUNIOR
%Exercício 3.9
clear all
close all
clc
%% Função de transferencia
G=tf(1,[1 1 0]);
%Tempo de amostragem
h=0.5;
%Função de transferencia discretizada
Gd=c2d(G,h);
%Parametros da planta discretizada em forma de vetor
[Bd,Ad]=tfdata(Gd,'v');
%% Dados para o sistema em malha fechada
%Parametros usados para o sistema desejado em malha fechada
csi=0.5; %coeficiente de amortecimento
Wn=1.5; %frequencia natural
% Pólos discretos desejados
pdes=exp(-csi*Wn*h + j*Wn*sqrt(1-csi^2)*h);
P=[pdes conj(pdes)];
% Função de transferencia em malha fechada
Am=poly([pdes conj(pdes)]);
Bm1=[polyval(Am,1) 0];
% Sistema desejado em malha fechada discretizado
Gmd1=tf(Bm1,Am,h);
% Parâmetros da planta desejada em malha fechada em forma de vetor
[Bmd,Amd]=tfdata(Gmd1,'v');
%% Parametros para o encontrar o controlador
b0=Bd(2);
b1=Bd(3);
a1=Ad(2);
a2=Ad(3);
bm0=Bmd(2);
am1=Amd(2);
am2=Amd(3);
a0=0;
%% Beta
beta=(1+am1+am2)/(b0+b1);
%% Minha nova FT desejada em MF
Am=poly([pdes conj(pdes)]);

39. Bm2=[beta*b0 beta*b1];
Gmd2=tf(Bm2,Am,h);
[Bmd2,Amd2]=tfdata(Gmd2,'v');
%% Valor de Entrada para a Onda Quadrada (uc);
N=input(' Entre com o numero de Interações?:');
%% Sinal de entrada Onda Quadrada;
j=0;
while j<N
for j=j+1:j+25
uc(j)=1;
end
for j=j+1:j+25
uc(j)=-1;
end
end
%% Condições iniciais necessários para o MQR
% Número de realizações
N = length(uc);
lambda = 0.98;%Fator de esquecimento
P0 = diag([100 100 1 1]); % Inicializar a matriz de covariância
Teta0 = [0 0 0.01 0.2]'; % Inicializar o vetor de parâmetros Teta
estimado
fi0=[0 0 0 0]';
yest=[0 0 0]';
diagP=diag(P0)';
%Número de parametros a serem estimados
Teta=[Teta0 Teta0 Teta0];
fi=[fi0 fi0 fi0];
%Comportamento da matriz de covariancia
diagP=[diagP; diagP; diagP];
P=P0;
cont=0*Teta;
y=0*yest;
u=0*yest;
erro=0*yest;
for k = 3:N
%% MQR
%Calcula a saída atual
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2); % Saída da planta
%Atualiza fi
fi(:,k-1)=[-y(k-1) -y(k-2) u(k-1) u(k-2)]';
%Calcula o erro de estimação
erro(k)=y(k)-fi(:,k-1)'*Teta(:,k-1);
%Calcula o vetor de ganhos
K=P*fi(:,k-1)/(lambda+fi(:,k-1)'*P*fi(:,k-1));
%Calcula o novo vetor de estimação de parâmetros
Teta(:,k)=Teta(:,k-1)+K*erro(k);
%Atualiza a matriz de covariância
P=(P-K*fi(:,k-1)'*P)/lambda;
diagP=[diagP; diag(P)'];
%Armazena parâmetros
a1est = Teta(1,k);
a2est = Teta(2,k);

40. b0est = Teta(3,k);
b1est = Teta(4,k);
%% Valores dos polinômios R, S e T
r1=((a0*am2)*(b0est^2)+(a2est-am2-a0*am1)*(b1est*b0est)+(a0+am1-
a1est)*(b1est^2))/(b1est^2-b1est*b0est*a1est+a2est*(b0est^2));
s0=((b1est*(a0*am1-a2est-am1*a1est+(a1est^2)+am2-
a1est*a0))/((b1est^2)-
b1est*b0est*a1est+a2est*(b0est^2)))+((b0est*(am1*a2est-a1est*a2est-
a0*am2+a0*a2est))/((b1est^2)-b1est*b0est*a1est+a2est*(b0est^2)));
s1=((b1est*(a1est*a2est-am1*a2est+a0*am2-a0*a2est))/((b1est^2)-
b1est*b0est*a1est+a2est*(b0est^2)))+((b0est*(a2est*am2-(a2est^2)-
a0*am2*a1est+a0*a2est*am1))/((b1est^2)-
b1est*b0est*a1est+a2est*(b0est^2)));
t0 = (1+am1+am2)/(b0est+b1est);
% Armazena parâmetros do controlador
cont(:,k)=[r1 s0 s1 t0]';
%% Cálculo da lei de controle
% Sinal de controle
u(k)=-r1*u(k-1)+t0*uc(k)-s0*y(k)-s1*y(k-1);
% Limite do sinal de controle
if u(k)>=4,
u(k)=4;
elseif u(k)<=-4,
u(k)=-4;
end
end
%% Sinais de Entrada e Saida do Processo;
figure(1)
subplot(211)
grid on
hold on
plot(uc,'k--')
%Subplot(312)
plot(y,'b')
legend('Sinal de referência (uc)','Sinal de saída (y)')
xlabel('Amostras')
title('Saída e Referência');
%xlim([0 100])
%% Sinal de Controle;
subplot(212)
stairs(u,'r')
grid on
legend('Sinal de controle (u)')
xlabel('Amostras')
title('Sinal de Controle');
%xlim([0 100])
%% Parâmetros a1 e a2 do Processo real e estimados;
figure(2)
subplot(211)
hold on
stairs(Teta(1,:),'c')
a1=-1.6065*ones(1,N);
plot(a1,'k-.')
stairs(Teta(2,:),'b')

41. a2=0.6065*ones(1,N);
grid on
plot(a2,'k--')
legend('a1 estimado','a1 real','a2 estimado','a2 real')
xlabel('Amostras')
ylabel('Amplitude')
title('Parâmetros a1 e a2 estimados');
%xlim([0 100])
%% Parâmetros b0 e b1 do Processo real e estimados;
subplot(212)
hold on
stairs(Teta(3,:),'g')
b0=0.1065*ones(1,N);
plot(b0,'k-.')
stairs(Teta(4,:),'r')
b1=0.0902*ones(1,N);
grid on
plot(b1,'k--')
legend('b0 estimado','b0 real','b1 estimado','b1 real')
xlabel('Amostras')
ylabel('Amplitude')
title('Parâmetros b0 e b1 estimados');
%xlim([0 100])
%% Parâmetros do controlador r1, s0, s1 e t0
figure(3)
subplot(221)
hold on
stairs(cont(1,:),'y','LineWidth',2)
r1=0.1111*ones(1,N);
grid on
plot(r1,'k-.')
legend('r1 estimado','r1 real')
xlabel('Amostras')
title('Parâmetro r1 do controlador');
subplot(222)
hold on
stairs(cont(2,:),'r','LineWidth',2)
a2=1.6422*ones(1,N);
grid on
plot(a2,'k-.')
legend('s0 estimado','s0 real')
xlabel('Amostras')
title('Parâmetro s0 do controlador');
subplot(223)
hold on
stairs(cont(3,:),'b','LineWidth',2)
a3=-0.7471*ones(1,N);
grid on
plot(a3,'k-.')
legend('s1 estimado','s1 real')
xlabel('Amostras')
title('Parâmetro s1 do controlador');
subplot(224)
hold on
stairs(cont(4,:),'g','LineWidth',2)
a4=0.8951*ones(1,N);
grid on
plot(a4,'k-.')
legend('t0 estimado','t0 real')

42. xlabel('Amostras')
title('Parâmetro t0 do controlador');
//////////////////////////////////////////////////////////////////////
//////////////////////PROBLEMAS: 3.6/ 3.7/ 3.9/ 3.11//////////////////
%% STR indireto usando MQR e MDPP
% Astrom & Wittenmark, Exemplo 3.4, p.104
% Prof. André Ferreira - 29/01/2014
%MODIFICADO POR PEDRO JUNIOR
clear all
close all
clc
%% Definição da planta
%g=tf(1,[1 1 0]); % Planta analógica
g=tf(1,[1 2 1]); % Planta analógica do problema 3.11
Ts=0.5; % Intervalo de amostragem
gd=c2d(g,Ts); % Planta discretizada
% Parâmetros da planta
[numd,dend]=tfdata(gd,'v');
b0=numd(2);
b1=numd(3);
a1=dend(2);
a2=dend(3);
%% Sistema em MF desejado
csi=0.7;
Wn=1;
% Pólos discretos desejados
pdes=exp(-csi*Wn*Ts + j*Wn*sqrt(1-csi^2)*Ts);
Pdes=[pdes conj(pdes)];
% FT desejada em MF
Am=poly([pdes conj(pdes)]);
Bm=[polyval(Am,1) 0]; % Escolhido para ter ganho DC unitário
gmd=tf(Bm,Am,Ts);
% Parâmetros da planta desejada em MF
[nummd,denmd]=tfdata(gmd,'v');
bm0=nummd(2);
am1=denmd(2);
am2=denmd(3);
%Polinômio A0:
a0=0; %Este parâmetro é sugerido no próprio livro
A0=tf([1 a0],[1],0.5);
%% Vetor de Entrada - Onda Quadrada (u)
uc = [];
neg=-1*ones(1,25);
pos=ones(1,25);
for i = 1:3

43. uc = [uc pos neg];
end
%% Condições iniciais necessários para o MQR
N = length(uc); % Número de realizações (medidas)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%
%lambda = 1;
%lambda = 0.85;
lambda = 0.65;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%
%P0 = diag([200 200 2 2]); % Inicializar a matriz de covariância *****
P0 = diag([100 100 1 1]); % Inicializar a matriz de covariância *****
%P0 = diag([50 50 0.5 0.5]); % Inicializar a matriz de covariância
*****
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%
Teta0 = [0 0 0.01 0.2]'; % Inicializar o vetor de parâmetros Teta
estimado *****
%Teta0 = [0 0 0.1 2]'; % Inicializar o vetor de parâmetros Teta
estimado *****
%Teta0 = [0 0 1 20]'; % Inicializar o vetor de parâmetros Teta
estimado *****
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%
fi0=[0 0 0 0]';
yest=[0 0 0]';
diagP=diag(P0)';
Teta=[Teta0 Teta0 Teta0];
fi=[fi0 fi0 fi0];
diagP=[diagP; diagP; diagP];
P=P0;
cont=0*Teta;
y=0*yest;
u=0*yest;
erro=0*yest;
for k = 4:N
%% MQR
% ----- Calcula a saída atual
y(k)=-a1*y(k-1)-a2*y(k-2)+b0*u(k-1)+b1*u(k-2); % Saída da
planta
% y(k)= -a1*y(k-2)-a2*y(k-3)+b0*u(k-1)+b1*u(k-2);
% ----- Atualiza Fi
fi(:,k-1)=[-y(k-1) -y(k-2) u(k-1) u(k-2)]';
% ----- Calcula o erro de estimação
erro(k)=y(k)-fi(:,k-1)'*Teta(:,k-1);
% ----- Calcula o vetor de ganhos
K=P*fi(:,k-1)/(lambda+fi(:,k-1)'*P*fi(:,k-1));
% ----- Calcula o novo vetor de estimação de parâmetros
Teta(:,k)=Teta(:,k-1)+K*erro(k);
% ----- Atualiza a matriz de covariância
P=(P-K*fi(:,k-1)'*P)/lambda;

44. diagP=[diagP; diag(P)'];
% ----- Armazena parâmetros
a1est = Teta(1,k);
a2est = Teta(2,k);
b0est = Teta(3,k);
b1est = Teta(4,k);
%Operador de Transferência:
%am1=Amq(2);
%am2=Amq(3);
beta=((1+am1+am2)/(b0est+b1est));
bm0=beta*b0est;
bm1=beta*b1est;
Hmq=tf([bm0 bm1],[1 am1 am2],0.5);
%% PASSO 2 - valores dos polinômios R, S e T
% r1 = b1est/b0est;
% s0 = (am1-a1est)/b0est;
% s1 = (am2-a2est)/b0est;
% t0 = bm0/b0est;
% cont(:,k)=[r1 s0 s1 t0]';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%5
%Coeficientes r1, s1 e s0:
r1=((a0*am2*(b0est*b0est))+((a2est-am2-a0*am1)*(b1est*b0))+((a0+am1-
a1est)*(b1est*b1est)))/((b1est*b1est)-
(b1est*b0est*a1est)+(a2est*(b0est*b0est)));
s1=((a0*am2)-(a2est*r1))/(b1est);
s0=((am1+a0)-(r1+a1est))/(b0est);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%Polinômios R, S e T:
R=tf([1 r1],1,0.5);
S=tf([s0 s1],1,0.5);
t0= beta*1;
t1= beta*a0;
T=tf([t0 t1],1,0.5);
cont(:,k)=[r1 s0 s1 t0]';
% %Polinômios R, S e T:
%R= tf([1 b1/b0],1,0.5); %tf([1 r1],1,0.5);
%S=tf([s0 s1],1,0.5);
%t0= beta*1;
%t1= beta*a0;
%T= tf([(bm0/b0) 0],1,0.5); %tf([t0 t1],1,0.5);
%% PASSO 3 - cálculo da lei de controle
u(k)=-r1*u(k-1) +t0*uc(k) -s0*y(k) -s1*y(k-1); % Sinal de controle
% Limite do sinal de controle
if u(k)>=4,
u(k)=4;
elseif u(k)<=-4,

45. u(k)=-4;
end
end
subplot(221)
hold on
plot(uc,'r--')
plot(y,'b')
legend('uc','y')
xlabel('Amostras')
title('Saída e Referência');
subplot(223)
stairs(u,'b')
legend('u')
xlabel('Amostras')
title('Sinal de Controle');
subplot(224)
stairs(cont')
legend('r1','s0','s1','t0')
xlabel('Amostras')
title('Parâmetros do Controlador');
subplot(222)
stairs(Teta')
legend('a1','a2','b0','b1')
xlabel('Amostras')
title('Parâmetros Estimados');
hold off