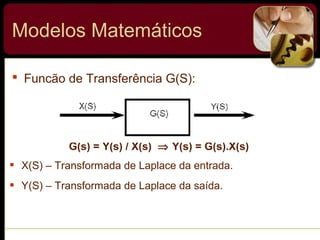
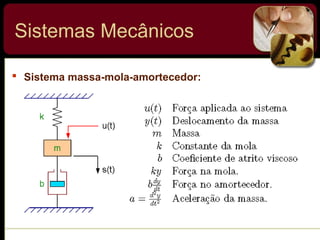
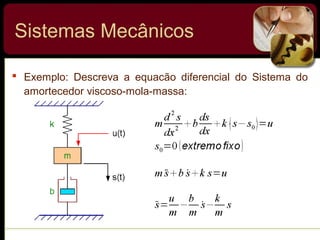
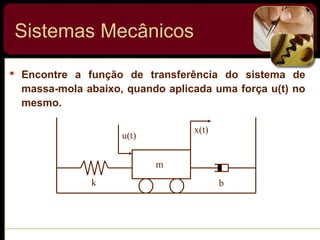
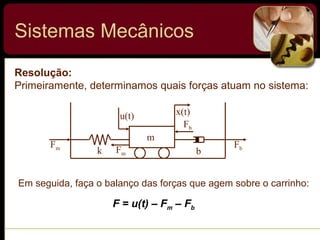
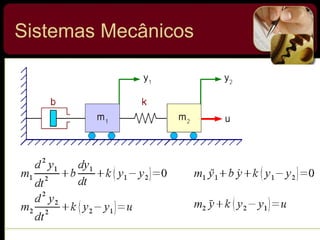
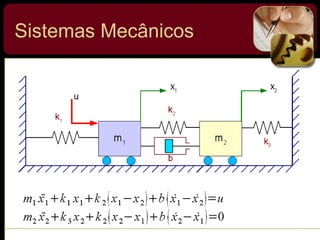
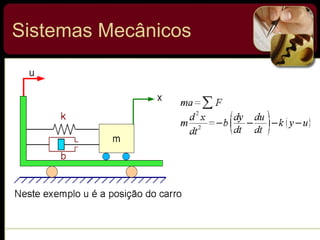
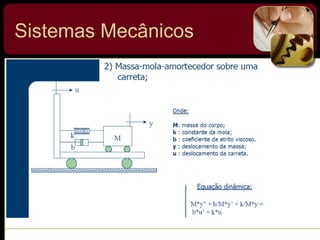
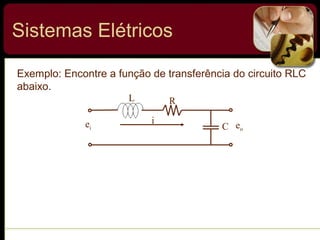
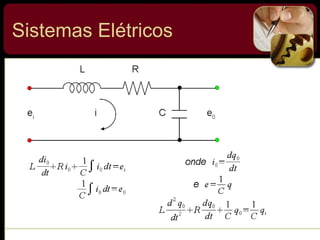
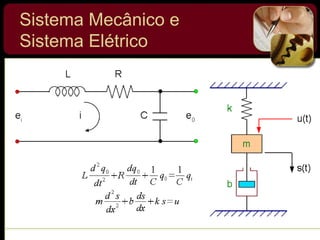
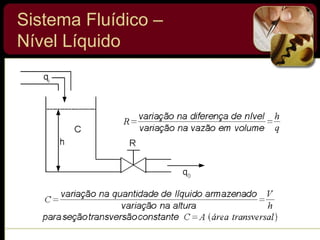
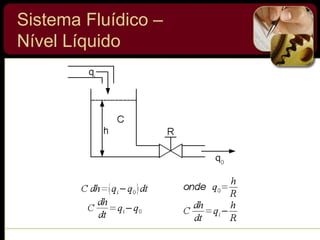
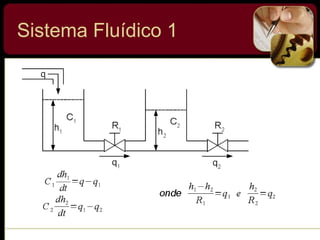
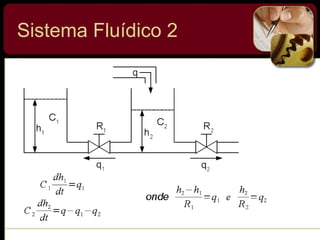
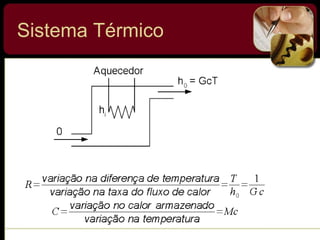
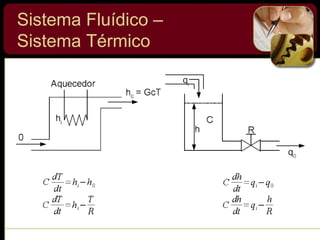
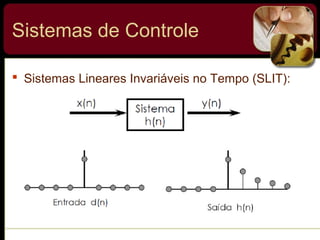
O documento discute sistemas de controle e fornece exemplos de diferentes tipos de sistemas, incluindo mecânicos, elétricos, fluídicos e térmicos. Apresenta conceitos-chave como modelo matemático, sistema linear, função de transferência e transformada de Laplace. Fornece exemplos de resolução de exercícios envolvendo sistemas mecânicos e elétricos.









![Modelos Matemáticos
Transformada de Laplace
∫
∞
−
0
dte st
f(t) = uma função de tempo t em que f(t) = 0 para t < 0
s = uma variável complexa
F(s) = transformada de Laplace de f(t)
L = Operador de Laplace - um símbolo operacional que
indica que a grandeza que ele antecede vai ser
tranformada por meio da integral de Laplace
Então, a transformada de Laplace de f(t) é dada por:
∫
∞
−
=
0
dttfesF st
)()(L [f(t)]=](https://image.slidesharecdn.com/docmodelagem492246747-140320151240-phpapp01/85/Doc-modelagem-_492246747-11-320.jpg)