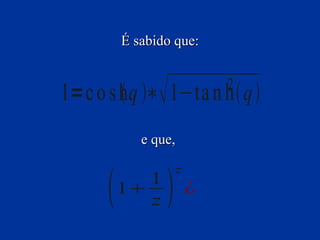O documento descreve de forma humorística como expressões matemáticas simples podem ser escritas de forma mais "elegante" e complicada, usando notação e conceitos avançados de forma desnecessária. A mensagem final sugere enviar o texto para outras pessoas como engenheiros e advogados, que supostamente gostariam de complicar explicações simples.

1. Elegância Profissional ...
Qualquer Engenheiro aprende a notação matemática
segundo a qual a soma de dois números reais, como
por exemplo,
11=2
pode ser escrita de maneira muito simples.
Entretanto, esta forma é errada devido à sua
banalidade e demonstra uma falta total de estilo.

2. Desde as primeiras aulas de Matemática sabemos que,
1=lne
e também que,
2 2
1=sin  p cos  p 
Além disso, todos sabem que,
∞ n
2= ∑
n= 0
 
1
2

3. Portanto a expressão,
11=2
pode ser reescrita de uma forma mais elegante como,
∞ n
ln  e  sin  p cos  p = ∑
2 2
n=0

1
2
a qual, como facilmente podem observar, é muito mais
compreensível e científica.

4. É sabido que:
1=c o s h q ∗ 1−ta n h q
 2
e que,
z
 1
1
z  ¿

5. de onde resulta,
∞ n
ln  e  sin  p cos  p = ∑
2 2
n=0

1
2
que ainda pode ser escrita da seguinte forma clara e
transparente,
2 ∞
cosh q ∗1−tanh  q 2
 
1
1 ¿ ¿sin  p cos  p = ∑
z
2 2
n=0 2 n
¿

6. Tendo em conta que
0!=1
e que a matriz invertida da matriz transposta é igual à
matriz transposta da matriz invertida (com a hipótese
de um espaço unidimensional), conseguimos a
seguinte simplificação (devida ao uso de notação
X vetorial),
−1 T
 X  − X  =0
T −1

7. Se unificarmos as expressões simplificadas,
0!=1
e
T −1 −1 T
 X  − X  =0
será óbvio que obtenhamos,
  X  −  X   ! =1
T −1 −1 T

8. Aplicando as simplificações descritas anteriormente,
resulta que, da equação abaixo…
2 ∞
cosh q ∗1−tanh2  q 
  1
1 ¿¿sin2  p cos2  p = ∑
z n=0 2 n
¿
…obtemos finalmente, de forma totalmente elegante,
legível, sucinta e compensível para qualquer um,
a equação:
2 ∞
cosh q ∗1−tan h2  q 
  X T −1
 − X −1 T
  1

!+ ¿¿sin2  p co s2  p =∑
z n =0 2 n
¿
(que, convenhamos, é muito mais profissional que
a vulgaríssima e plebéia equação original )
11=2

9. Envie esta mensagem a alguma pessoa sábia e inteligente.
Envie, também, para os advogados da sua lista para que eles
saibam que não são os únicos que sabem complicar as coisas
simples em proveito próprio.
Envie-a também a seus amigos, que saberão apreciar sua
alma sensível e humilde de Engenheiro(a)…