O documento discute algoritmos para encontrar caminhos de menor custo em grafos. Apresenta o algoritmo de Dijkstra para grafos sem arestas de custo negativo e o algoritmo de Bellman-Ford para grafos que podem conter ciclos de custo negativo, podendo detectá-los. Explica a implementação e análise da complexidade de ambos, com exemplos de problemas clássicos onde podem ser usados.

1. TREINAMENTO PARA COMPETIÇÕES DE
PROGRAMAÇÃO
GRAFOS - PARTE III
SINGLE-SOURCE SHORTEST PATHS:
DIJKSTRA E BELLMAN-FORD
Murilo Adriano Vasconcelos
http://murilo.wordpress.com

2. O problema
• Dado um grafo ponderado G(V, E), onde as
arestas tem custos positivos, queremos
saber qual o custo do menor caminho de
um vértice origem u ∈ V para todos os
outros vértices v ∈ V.

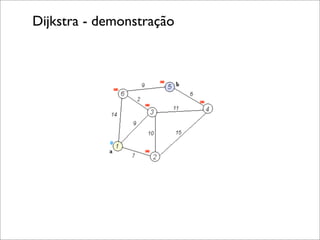
3. O algoritmo de Dijkstra
const int MAXV = 1000; // número máximo de vértices
const int INF = 0x3f3f3f3f; // cuidado com esse valor
list< pair<int, int> > grafo[MAXV]; // lista de adjacência
int dist[MAXV]; // a resposta ficará neste vetor
int visited[MAXV], N; // N é a quantidade de vértices atual
void leitura()
{
cin >> N >> m; // quantidade de vertices e arestas
int de, para, custo;
// limpa o grafo
for (int i = 0; i < N; ++i) g[i].clear();
// leitura da entrada
for (int i = 0; i < m; ++i) {
cin >> de >> para >> custo;
g[de].push_back(make_pair(para, custo));
}
}

4. O algoritmo de Dijkstra
void dijkstra(int origem)
{
for (int i = 0; i < N; ++i) {
dist[i] = INF;
visited[i] = false;
}
// nossa heap de máximo onde: first = custo,
// second = vertice
priority_queue< pair<int, int> > pq;
pq.push(make_pair(0, origem));
dist[origem] = 0; // distancia da origem pra ela
// mesma é 0
pair<int, int> atual;
list< pair<int, int> >::iterator it;

5. O algoritmo de Dijkstra
while (!pq.empty()) {
atual = pq.top();
pq.pop();
int custo = -atual.first; // nao esqueça do ‘-’!
int v = atual.second;
if (visited[v]) continue; // já processamos ele
visited[v] = true; // se cheguei aqui, o menor custo
// de origem para v já foi calculado
// para cada aresta, tentamos fazer a relaxação
for (it = g[v].begin(); it != g[v].end(); ++it) {
if (dist[it->second] > w + it->first) {
dist[it->second] = w + it->first;
pq.push(make_pair(-dist[it->second],
it->second));
}
}
}
} // dijkstra

6. O algoritmo de Dijkstra
• Inicialmente, colocamos na heap, o vértice
de origem com o custo 0 e dizemos que o
custo da origem para origem é 0
• Em seguida, para cada elemento v com o
menor custo (top() na priority_queue),
tentamos relaxar (diminuindo) o custo dos
seus vizinhos
• Se o custo de algum vértice u for maior
que o custo de v mais o custo da aresta
que liga o v a u, diminuímos o custo de u
para este valor

7. Dijkstra - demonstração

8. Dijkstra - análise
• Complexidade O(|E| log |V|)
• |V| = 1000, |E| = 100.000 < 10^6
operações (feasible)
• Comparativo com Floyd-Warshall O(|V|^3)
• |V| = 1000, 10^9 operações (geralmente
unfeasible)

9. Outro problema
• Dado um grafo ponderado G(V, E), onde as
arestas podem ter custos negativos,
queremos saber qual o custo do menor
caminho de um vértice origem u ∈ V para
todos os outros vértices v ∈ V.

10. Usar o Dijkstra?
• Seja G, este grafo:
2
-1 -4
0 10 1 3 4
2 1

11. Usar o Dijkstra?
Seja G, este grafo:
2
-1 -4
0 10 1 3 4
2 1
Qual a menor distância entre 0 e 4?

12. Usar o Dijkstra?
Não podemos usar o Dijkstra, pois o grafo
contém um ciclo negativo.
2
-1 -4
0 10 1 3 4
2 1
Podemos ficar infinitamente neste ciclo pois o
custo sempre diminuirá

13. O algoritmo Bellman-Ford
• O algoritmo de Bellman-Ford encontra o
menor caminho entre um vértice origem e
todos os outros se o grafo não tiver ciclos
negativos
• Se o grafo tiver ciclos negativos, o algoritmo
serve para detectá-los

14. O algoritmo Bellman-Ford
• Utiliza a representação de lista de arestas
• Faz a relaxação utilizando a desigualdade
triangular |V| - 1 vezes
• Se após |V| - 1 relaxações, ainda
conseguirmos diminuir o custo de algum
vértice, o grafo contém ciclos negativos

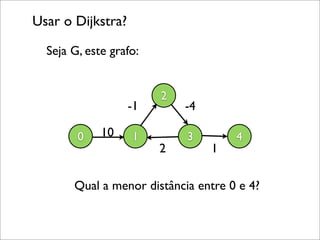
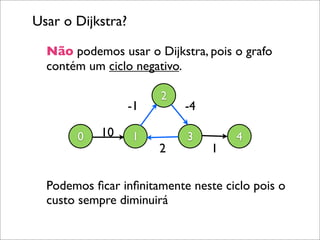
15. O algoritmo Bellman-Ford
const int MAXV = 1000; // número máximo de vértices
const int INF = 0x3f3f3f3f; // cuidado com esse valor
struct aresta { int u, v, w; }; // de, para, custo
vector<aresta> grafo; // pode ser um array se
// soubermos o máximo de arestas
int custo[MAXV], N, E; // custo, vértices, arestas
void le()
{
cin >> N >> E; // le a quant. de vértices e arestas
grafo.clear();
aresta ar;
for (int i = 0; i < E; ++i) {
cin >> ar.u >> ar.v >> ar.w; // de, para, custo
grafo.push_back(ar);
}
}

16. O algoritmo Bellman-Ford
bool bellan_ford(int origem)
{
for (int i = 0; i < V; ++i) custo[i] = INF;
custo[origem] = 0;
for (int i = 0; i < V - 1; ++i) { // até V - 1
for (int j = 0; j < E; ++j) {
int u = grafo[j].u;
int v = grafo[j].v;
int w = grafo[j].w;
// relaxação
if (custo[v] > custo[u] + w) {
custo[v] = custo[u] + w;
}
}
}

17. O algoritmo Bellman-Ford
// checagem de ciclos de custo negativo
for (int j = 0; j < E; ++j) {
int u = grafo[j].u;
int v = grafo[j].v;
int w = grafo[j].w;
// se ainda é possível diminuir o custo
// é porque sempre vai ter como (ciclo negativo)
if (custo[v] > custo[u] + w) {
return false; // ciclo encontrado
}
}
return true; // nenhum ciclo negativo
} // bellman_ford()

18. Bellman-Ford - análise
• Complexidade O(VE)
• Loop de fora V vezes, loop interno E
vezes

19. Alguns Problemas
Dijkstra (UVA):
341 - Non-Stop Travel
929 - Number Maze
1202 - Finding Nemo
10166 - Travel
10269 - Adventure of Super Mario
10278 - Fire Station
10389 - Subway
10603 - Fill
10801 - Lift Hopping
10986 - Sending email
11367 - Full Tank?
11377 - Airport Setup
11492 - Babel
11833 - Route Change
12138 - Chemical Plant
Bellman Ford (UVA):
558 - Wormholes
10557 - XYZZY
11280 - Flying to Fredericton

20. Dúvidas?