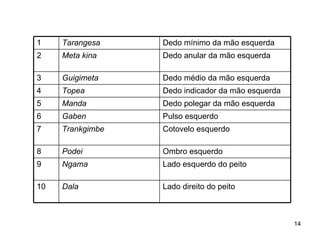
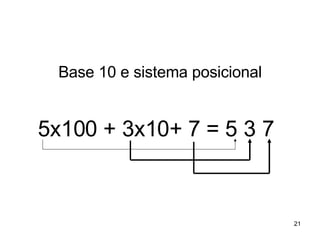
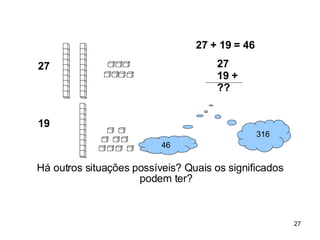
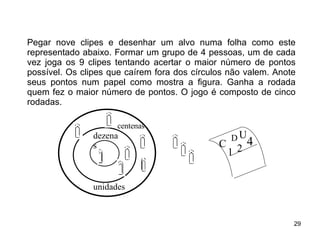
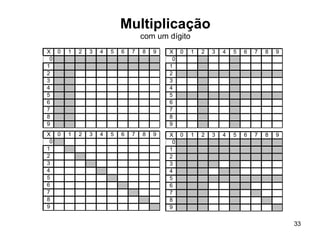
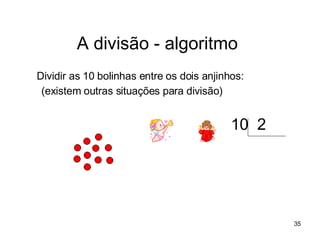
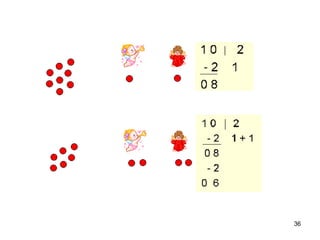
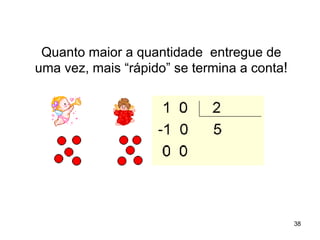
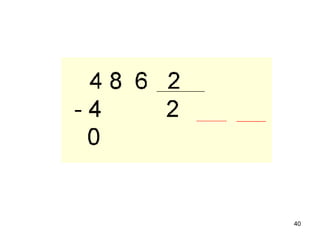
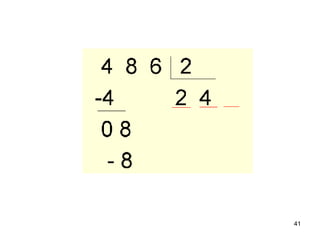
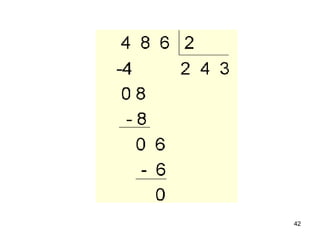
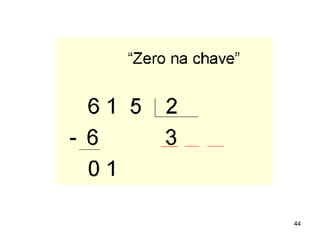
1) O documento descreve atividades didáticas para o ensino do sistema numérico decimal utilizando o Material Dourado de Montessori. 2) As atividades abordam conceitos como dezena, centena, adição, subtração e outras operações matemáticas. 3) O Material Dourado permite que as crianças explorem essas ideias de forma lúdica e concreta.

1. Uso do Material Dourado como recurso didático Atividades para a compreensão do Sistema Numérico Decimal Profa. Wania Tedeschi Agosto /2008

2. Tarefa: (Inspirada em KAMII, 2002) Vamos desenhar uma coleção com dezesseis objetos?

3. No desenho: - circular os objetos que representam o 6 do número 16; - grifar os objetos que representam o 1 do número 16.

9. Quais as possíveis interpretações? 1 2 3 4

10. VESTÍGIOS

11. Sistema egípcio – não posicional

12. Origem do nosso sistema de numeração Relação um-a-um com um conjunto de objetos partes do corpo Pedras, seixos, sementes, cortes...

13. Mudanças na escrita dos algarismos Século IX: Século XI: Século XI (árabes ocidentais): Século XVI (árabes orientais): Séculos XV e XVI (Europeus): Hoje: 1 2 3 4 5 6 7 8 9 0

14. Dedo mínimo da mão esquerda Tarangesa 1 Dedo anular da mão esquerda Meta kina 2 Dedo médio da mão esquerda Guigimeta 3 Dedo indicador da mão esquerda Topea 4 Cotovelo esquerdo Trankgimbe 7 Pulso esquerdo Gaben 6 Lado direito do peito Dala 10 Lado esquerdo do peito Ngama 9 Ombro esquerdo Podei 8 Dedo polegar da mão esquerda Manda 5

15. OUTRAS BASES Os povos que viveram na Mesopotâmia (hoje Iraque) usavam a base 60 . Herdamos e usamos até hoje as frações de 60 para medir o tempo . O porquê desta escolha parece ser a combinação dos hábitos de povos que contavam em dezenas (base 10) e de outros que contavam em dúzias (base 12). A base doze foi uma escolha inspirada na observação das doze luas que ocorrem em um ano , e que determinaram a criação de doze meses para o calendário. Mas é provável que esta escolha esteja principalmente associada à contagem feita com o auxílio das falanges exceto o polegar, que fazia a contagem. Na língua francesa atual, encontramos, na denominação de alguns números, vestígios de uma base 20 considerada pelos celtas (início da era cristã). Para se referir ao oitenta (80) os franceses dizem quatre-vingt , isto é, quatro vezes vinte (4 X 20).

16. O dia da semana Que dia do mês será o sábado daqui 3 semanas? O dia do mês Que dia do mês será daqui 38 dias? Trabalho com outras bases

17. Trabalho com outras bases O dia do mês Que dia do mês será daqui 38 dias? 8 de agosto + 38 dias = total de dias 46 dias. Mas o mês de agosto só tem 31 dias, Logo 46 –31 dias acabará resultando no dia 15 de setembro. O dia da semana Que dia do mês será o sábado daqui 3 semanas? 8 de agosto + 3 semanas = 8 de agosto + 3 x 7 = total de dias 29 dias. Logo será dia 29 de agosto. 21 dias

18. Base 10 Posicional Existência do Zero Princípio aditivo Princípio multiplicativo Características do sistema de numeração decimal

19. O ZERO Os números em geral estão inicialmente relacionados à objetos existentes, mas o zero seria contar o que não existe ou o que não está. É comum o zero ser apresentado como o nada ou a insignificância. QUAIS AS POSSÍVEIS CONSEQUÊNCIAS DESSAS ABORDAGENS? QUAL É A FUNÇÃO DO ZERO?

20. SER O INÍCIO DE UMA SÉRIE DE NÚMEROS NATURAIS? REPRESENTAR AQUILO QUE NÃO TEM VALOR? 0 , 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 2x100 + 0x10 + 7 = 2 0 7

21. 5x100 + 3x10+ 7 = 5 3 7 Base 10 e sistema posicional

22. O MATERIAL DOURADO Idealizado por Maria Montessori (1870-1953): contas amarelas Adaptado por Lubienska de Lenval: madeira SUGESTÕES: Primeiro contato deve ser de forma lúdica Inicialmente, as crianças atribuem nomes às peças Forma própria de registro (no papel)

23. Exemplos de atividades com o Material Dourado 1- Contato livre com o material O bjetivos: perceber a relação entre as peças; atribuir nomes às peças Depois de um tempo com as crianças manipulando as peças, o professor pode perguntar: -Quantos cubinhos necessito para formar uma barra? -Quantos cubinhos necessito para formar uma placa? -Quantas barras necessito para formar uma placa?

24. 2 – A dezena Objetivos: perceber o agrupamento das dezenas e as formas de registro. Em grupos de quatro, cada aluno joga um dado e toma tantos cubinhos quanto a quantidade obtida. O jogo segue até que alguém consiga dez cubinhos, ou mais. O professor questiona: Existe uma peça no Material Dourado que possa representar dez cubinhos? O professor sugere uma nova regra: cada dez cubinhos devem então, ser trocados por uma barra. O professor questiona: Como podemos registrar, no papel, a quantidade obtida por cada criança? (Esta atividade pode ser adaptada para o trabalho com centena e milhar)

25. 3 - JOGO DOS CARTÕES Objetivos: compreender o mecanismo do "vai um" nas adições; estimular o cálculo mental. O professor coloca no centro do grupo alguns cartões virados para baixo. Nestes cartões estão escritos números entre 10 e 30 . 1º sorteio: Um aluno do grupo sorteia um cartão . Os demais devem pegar as peças correspondentes ao número sorteado. Em seguida, um representante do grupo vai à lousa e registra em uma tabela os números correspondentes às quantidades de peças. 2º sorteio: Um outro aluno sorteia um segundo cartão . Os demais devem pegar as peças correspondentes a esse segundo número sorteado. Em seguida, o representante do grupo vai à tabela registrar a nova quantidade. Nesse ponto, juntam-se as duas quantidades de peças, fazem-se as trocas e novamente completa-se a tabela . Isto encerra uma rodada vence o grupo que tiver conseguido maior total.

26. Que relações a criança pode estabelecer com o mecanismo do vai um?

27. Há outros situações possíveis? Quais os significados podem ter? 46 316 27 + 19 = 46 19 27 27 19 + ??

28. 4 - O JOGO DE RETIRAR Objetivos: compreender a questão do "empresta um" nas subtrações com recurso; estimular o cálculo mental. Em cada rodada, os grupos sorteiam um cartão e uma papeleta. No cartão há um número e eles devem pegar as peças correspondentes a essa quantia. Na papeleta há uma ordem que indica quanto devem tirar da quantidade que têm. Por exemplo: cartão com número 72 e papeleta com a ordem: TIRE 35.

29. Pegar nove clipes e desenhar um alvo numa folha como este representado abaixo. Formar um grupo de 4 pessoas, um de cada vez joga os 9 clipes tentando acertar o maior número de pontos possível. Os clipes que caírem fora dos círculos não valem. Anote seus pontos num papel como mostra a figura. Ganha a rodada quem fez o maior número de pontos. O jogo é composto de cinco rodadas. unidades dezenas centenas C U 1 2 4 D

30. Reúna-se com mais dois colegas. Todos devem ter 400 pontos no início que devem ser anotados num papel. Em seguida, um de cada vez joga dois dados, um dos números que ficou para cima será o algarismo das dezenas e o outro das unidades. Forme o maior número que você puder com os dois dígitos e subtraia dos quatrocentos pontos. Ganha quem terminar primeiro com os pontos. Observe o exemplo: 4 0 0 - 4 1 3 5 9

31. Idéias da soma Juntar (origem da própria constituição dos números decimais) comparar Agrupar Representar

32. Idéias da subtração Retirar Comparar Completar

33. Multiplicação com um dígito

34. Multiplicação: Algoritmo Por que ficou um espaço vazio sob o 5 do 615? - O 246 escrito abaixo do 615 é duzentos e quarenta e seis?

35. A divisão - algoritmo Dividir as 10 bolinhas entre os dois anjinhos: (existem outras situações para divisão) 10 2

38. Quanto maior a quantidade entregue de uma vez, mais “rápido” se termina a conta !

39. Usando, o Material Dourado para compreender a operação:

43. Zero “na Chave ”

47. Referências: GUNDLACH,Bernard H. História dos números e numerais. São Paulo: Atual, 1992. KAMII, C.; HOUSMAN, L. B. Crianças pequenas reinventam a aritmética: implicações da teoria de Piaget. Porto Alegre: Artmed Editora, 2002. http://educar.sc.usp. br / matematica http ://www. iejusa . org . br / cienciaetecnologia / matematica . php http :// web . educom .pt/ escolovar / mat _normank12_somar.somas.parciais. ppt #1 http ://www. planetaeducacao .com. br http :// matematic a.com.sapo.pt/contar2.htm http:// educamat . ese . ipcb .pt http ://educar.sc.usp. br / matematica http://www.luisclaudio.mat.br http://cienciahoje.uol.com.br/materia/view/2051