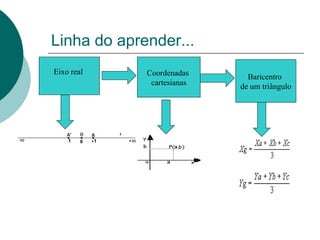
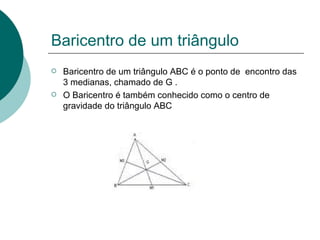
A Geometria Analítica é uma parte da Matemática que representa propriedades geométricas por meio de coordenadas cartesianas, permitindo resolver equações de planos, retas e curvas. Foi desenvolvida no século XVII por René Descartes e utiliza dois eixos perpendiculares para definir a posição de pontos através de suas coordenadas. O documento explica conceitos como eixo real, coordenadas cartesianas e o baricentro de um triângulo.

1. Objeto de aprendizagem em Geometria Analítica Adriana Belchior Sargaço Pólo São João da Boa Vista – SP Curso NTEM

2. O início.... A Geometria Analítica é uma parte da Matemática. A Geometria Analítica também era chamada de Geometria de Coordenadas e que bem antes recebia o nome de Geometria Cartesiana. O sistema de coordenadas cartesianas é utilizado para a resolução de equações de planos, retas, curvas e círculos. Os estudos iniciais da Geometria Analítica se deram no século XVII e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas.

3. Abaixo estão descritos uma síntese sobre: - Eixo real - Coordenadas cartesiana - Baricentro de um triângulo

4. Linha do aprender... Eixo real Coordenadas cartesianas Baricentro de um triângulo

5. Eixo real Seja a reta r com um ponto O chamado de origem. Devemos adotar uma unidade de medida, sendo os comprimentos a partir de O positivos a direita e negativos a esquerda. A medida do segmento AO é igual a 1. Os números são chamados de abscissas dos pontos. Então a abscissa do ponto A´é -1 , a abscissa da origem O é 0 e a abscissa do ponto A é 1.

6. Coordenadas Cartesianas Para compreender coordenadas cartesianas é necessário que 2 retas perpendiculares intercedam num ponto O, que será a origem do no ponto zero. A abscissa do ponto P será a e b será a ordenada do ponto P. O eixo OX é chamado de eixo das abscissas e o OY é chamado de eixo das ordenadas. O ponto O (0,0) é chamado de origem do plano cartesiano Os números representam as regiões do plano chamados de Quadrantes. Temos 4 quadrantes, sendo o 1º quadrante a e b positivos; no 2º quadrante a é negativo e b é positivo; no 3º quadrante os dois são negativos e no 4º quadrante a é positivo e b é negativo.

7. Baricentro de um triângulo Baricentro de um triângulo ABC é o ponto de encontro das 3 medianas, chamado de G . O Baricentro é também conhecido como o centro de gravidade do triângulo ABC

8. Curiosidades da Geometria A Geometria está presente em tudo que nos rodeia, apesar de muitas vezes nem tomarmos o conhecimento disso. Através das formas,desenhos e das propriedades geométricas. Na Natureza podemos encontrar diversas formas geométricas, como no favo das colméias, na teia de uma aranha, na simetria das borboletas. Dentre as profissões, nos dias atuais muitos pedreiros utilizam as formas geométricos na colocação de pisos, azulejos. O marceneiro utiliza muito a geometria na montagem de um telhado fazendo as descrição na altura, na queda do telhado em relação a queda d´água.

9. A Simetria no Contexto Geométrico A aprendizagem no ensino da Geometria pode-se utilizar o software Geogebra como instrumento educacional na construção de figuras geométricas simétricas, como vemos abaixo demonstrado.

10. Simetria no Geogebra

11. Simetria Uso da geometria no ladrilho das casas

12. Simetria A simetria na asa das borboletas

13. Simetria Simetria na arte

14. Simetria Formas de simetria na Natureza

15. Referência http://www.desenho.org/exercicios http://www.professores.uff.br//hjibortol/cederj/applets/car/mgal-baricentro-01 http://busca.uol.com.br/imagem/index.html?q=figura+de+um+baricentro+no+triangulo&ad=on http://osalunosqueexploravam.blogspot.com/2009_08_01_archive.html http://www.ime.usp.br/~brolezzi http://www.mat.ufrgs.br/~edumatec/software/softw.html http://www.mat.ufmg.br/gaal/aplicacoes.html http://www.algosobre.com.br/matematica/geometria-analitica.html http://www.geogebra.com.br http://www.somatematica.com.br