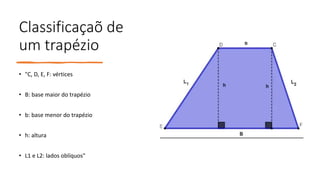
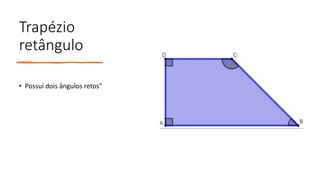
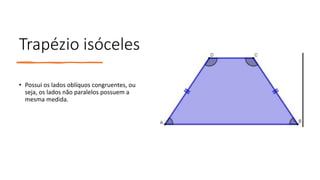
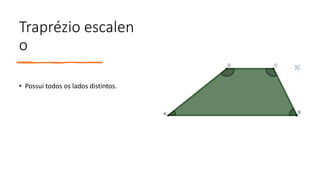
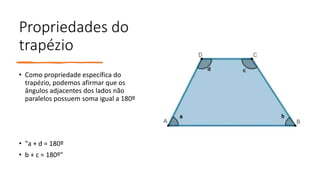
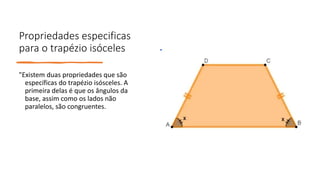
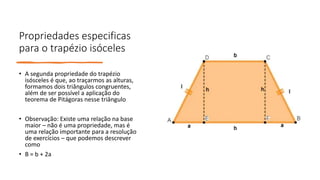
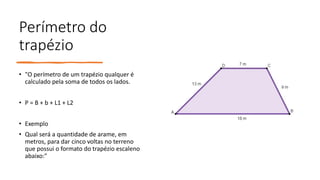
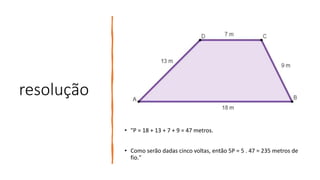
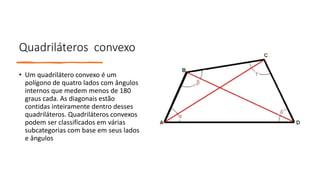
Os principais pontos abordados no documento são: 1) Quadriláteros possuem 4 lados, 4 ângulos internos e 4 vértices. 2) Existem quadriláteros notáveis como paralelogramos, quadrados, retângulos e losangos. 3) São apresentadas fórmulas para calcular a área de quadrados, retângulos, losangos e trapézios.

1. TRABALHO DE
MATEMATICA
QUADRILATEROS
Alunos: Yasmin, Ana Lídia e Ana vitória

2. OQUE SÃO OS
QUADRILÁTEROS?
• Os Quadrilátero são polígonos que possuem 4 lados e podem ser
classificados como convexos ou côncavos. Além disso, são
compostos por 4 lados, 4 ângulos internos e 4 vértices. A soma
dos ângulos internos de um quadrilátero é igual a 360°.
• Existem alguns casos especiais de quadriláteros, conhecidos
como quadriláteros notáveis, que são: paralelogramo, quadrado,
retângulo, losango e trapézio
• Essa figura geométrica bidimensional é formada por:
• Lados: são os segmentos da reta que formam o contorno do
polígono
• Vértices: são os pontos dos segmentos da reta
• Ângulo: são quatro ângulos internos que somam 360
• Diagonais: são duas diagonais que ligam dois vértices não
consecutivo

3. COMO ACHAR A ÁREA DE UM QUADRILÁTERO
• COMO IDENTIFICAR UM PARALELOGRAMO.
• Um PARELELOGRAMO é toda forma de quatro lados que possui dois pares de lados paralelos, sendo
que os lados opostos apresentam o mesmo comprimento. paralelogramos incluem
• QUADRADOS
• Quatro lados, todos com mesma medida. quatro cantos, todos eles com ângulos de 90graus (ângulos
retos).
• RETÂNGULOS Quatro lados, sendo que os opostos apresentam igual comprimento quatro cantos, todos
com ângulos de 90 graus.
• LOSANGOS
• Quatro lados, sendo que os opostos apresentam igual comprimento quatro cantos-nenhum deles
possui um ângulo de 90 graus, mas todos os opostos devem apresentar ângulos de iguais medida.

4. Quadriláteros convexo
• Um quadrilátero convexo é um
polígono de quatro lados com ângulos
internos que medem menos de 180
graus cada. As diagonais estão
contidas inteiramente dentro desses
quadriláteros. Quadriláteros convexos
podem ser classificados em várias
subcategorias com base em seus lados
e ângulos

5. Quadriláteros
não convexos
• Um quadrilátero côncavo pode não ser a forma de
quatro lados da variedade pré-escolar comum, mas
ainda é um polígono. Quadriláteros côncavos são
polígonos de quatro lados que têm um ângulo interno
que excede 180 graus. Outro meio de determinar se
um quadrilátero é côncavo é verificar as diagonais , ou
o segmento de linha que conecta os vértices não
adjacentes. Se qualquer parte de uma diagonal estiver
no exterior do quadrilátero, então o quadrilátero é
côncavo. Se uma forma for côncava, ela parecerá ter
um lado que foi empurrado para dentro ou uma
caverna. Veja os exemplos dos quadriláteros côncavos
e convexos

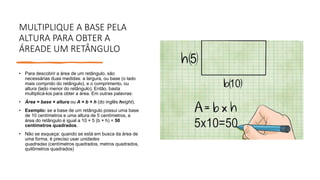
6. Multiplique um lado por ele mesmo para
descobrir a área de um quadrado
• Basicamente, quadrados são retângulos especiais, de modo que é
possível usar a mesma fórmula para descobrir sua área. No entanto,
uma vez que os lados de um quadrado apresentam todos a mesma a
mesma medida, é possível usar atalho de multiplicas um lado por ele
mesmo. Realizar esse cálculo é igual á multiplicação de base do
quadrado apresentam todos a mesma medida, é possível usar o atalho
de multiplicar um lado por ele mesmo. Realizar esse cálculo é igual a
multiplicação da base do quadrado por sua altura, uma vez que ambas
as medidas serão sempre as mesmas. Use a seguinte equação:[1]
• Área=lado*lado, A=s2(do inglês Side) ou A=h2
• EXEMPLO: se um lado do quadrado apresentar o
comprimento de 4 metros(s=4) sua área será
simplesmente igual a s2 OU 4*4=16 METROS
QUADRADOS.

7. MULTIPLIQUE A BASE PELA
ALTURA PARA OBTER A
ÁREADE UM RETÂNGULO
• Para descobrir a área de um retângulo, são
necessárias duas medidas: a largura, ou base (o lado
mais comprido do retângulo), e o comprimento, ou
altura (lado menor do retângulo). Então, basta
multiplicá-los para obter a área. Em outras palavras:
• Área = base × altura ou A = b × h (do inglês height).
• Exemplo: se a base de um retângulo possui uma base
de 10 centímetros e uma altura de 5 centímetros, a
área do retângulo é igual a 10 × 5 (b × h) = 50
centímetros quadrados.
• Não se esqueça: quando se está em busca da área de
uma forma, é preciso usar unidades
quadradas (centímetros quadrados, metros quadrados,
quilômetros quadrados)

8. Multiplique as diagonais e Divida o resultado
por dois para encontrar a área de um losango
• Tome cuidado nessa equação -quando você está
tentando descobrir a área de um losango, Não se pode
simplesmente multiplicar dois lados adjacentes. Em vez
disso encontre as diagonais (as linhas que conectam
cada conjunto de cantos opostos), multiplique-as e
divida o resultado por dois. Em outras palavras:[2]
• Área = (diagonal 1* diagonal 2) /2 ou A =
(d1 *d2/2.
• EXEMPLO: se um losango possui diagonais com
comprimentos iguais 6 e 8 metros
respetivamente, sua área será igual a (6*8) /2 =
48/2=24 metros quadrados

9. Elementos
de um
trapézio
• Definimos como trapézio todo quadrilátero que possui dois lados
paralelos. Os lados paralelos são conhecidos como base maior e
base menor. Como todo quadrilátero, possui duas diagonais, e a
soma dos ângulos internos é igual a 360º.
• Os elementos do trapézio são:
• Quatro lados;
• Dois lados paralelos entre si e dois não paralelos;
• Quatro vértices;
• Quatro ângulos internos, cuja soma é igual a 360º;
• Duas diagonais.

10. Trapézio
• O trapézio é um polígono quadrilátero que possui exatamente dois lados
paralelos e dois lados oblíquos ."O trapézio é uma figura da geometria plana bastante
presente no nosso dia a dia. Trata-se de um polígono que possui quatro lados, sendo dois
lados paralelos (conhecidos como base maior e base menor) e dois não paralelos (lados
oblíquos). Como todo quadrilátero, ele possui duas diagonais, e a soma dos seus ângulos
internos é sempre igual a 360º.
• Um trapézio pode ser classificado como trapézio retângulo, quando possui dois ângulos
retos; trapézio isósceles, quando os lados não paralelos são congruentes, ou seja,
possuem a mesma medida; e trapézio escaleno, quando todos os lados possuem
medidas diferentes. O perímetro de um trapézio é calculado pela soma de seus lados, e
há fórmulas específicas para calcular a área e a mediana de Euler do trapézio."

11. Classificação do trapézio
• existem três possíveis classificações para um trapézio de acordo com o formato que ele
possui. Um trapézio pode ser retângulo, isósceles ou escaleno.

12. Classificaçaõ de
um trapézio
• "C, D, E, F: vértices
• B: base maior do trapézio
• b: base menor do trapézio
• h: altura
• L1 e L2: lados oblíquos"

13. Trapézio
retângulo
• Possui dois ângulos retos"

14. Trapézio isóceles
• Possui os lados oblíquos congruentes, ou
seja, os lados não paralelos possuem a
mesma medida.

15. Traprézio escalen
o
• Possui todos os lados distintos.

16. Propriedades do
trapézio
• Como propriedade específica do
trapézio, podemos afirmar que os
ângulos adjacentes dos lados não
paralelos possuem soma igual a 180º
• "a + d = 180º
• b + c = 180º"

17. Propriedades especificas
para o trapézio isóceles
"Existem duas propriedades que são
específicas do trapézio isósceles. A
primeira delas é que os ângulos da
base, assim como os lados não
paralelos, são congruentes.

18. Propriedades especificas
para o trapézio isóceles
• A segunda propriedade do trapézio
isósceles é que, ao traçarmos as alturas,
formamos dois triângulos congruentes,
além de ser possível a aplicação do
teorema de Pitágoras nesse triângulo
• Observação: Existe uma relação na base
maior – não é uma propriedade, mas é
uma relação importante para a resolução
de exercícios – que podemos descrever
como
• B = b + 2a

19. Perímetro do
trapézio
• "O perímetro de um trapézio qualquer é
calculado pela soma de todos os lados.
• P = B + b + L1 + L2
• Exemplo
• Qual será a quantidade de arame, em
metros, para dar cinco voltas no terreno
que possui o formato do trapézio escaleno
abaixo:"

20. resolução
• "P = 18 + 13 + 7 + 9 = 47 metros.
• Como serão dadas cinco voltas, então 5P = 5 . 47 = 235 metros de
fio."

21. Bibliografia