Ricardo Luiz Gerardi Braga é graduado em Licenciatura Plena em Matemática pela Universidade do Estado da Bahia e está cursando pós-graduação em Metodologia do Ensino da Matemática pelo Instituto de Conhecimento Latino-Americano. O documento apresenta conceitos fundamentais sobre limites de funções, incluindo exemplos e propriedades dos limites de constantes, soma, diferença, produto e quociente. Além disso, aborda limites de potências e raízes, e a noção de função contínua.





![O limite da soma de duas ou mais funções é igual a
soma dos limites dessas funções.
Lim [f(x)+ g(x)] = Lim f(x)+ Lim g(x)
X Xo
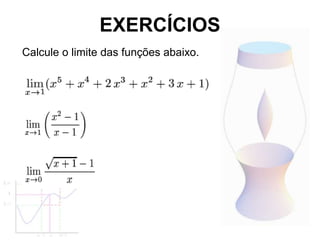
Exemplos:
X Xo X Xo
Lim (x+3) = Lim x + Lim 3
X 2 X 2 X 2
= 2 + 3 = 5
Limite da soma](https://image.slidesharecdn.com/apresentaolimite-230529151742-b11e17d6/85/APRESENTACAO-LIMITE-ppt-10-320.jpg)
![O limite da diferença de duas ou mais funções é igual a
diferença dos limites dessas funções.
Lim [f(x) - g(x)] = Lim f(x) - Lim g(x)
X Xo
Exemplos:
X Xo X Xo
Lim (2x - 5) = Lim 2x - Lim 5
X 2 X 2 X 2
= 4 - 5 = -1
Limite da diferença](https://image.slidesharecdn.com/apresentaolimite-230529151742-b11e17d6/85/APRESENTACAO-LIMITE-ppt-11-320.jpg)
![O limite do produto de duas ou mais funções é igual ao
produto dos limites dessas funções.
Lim [f(x).g(x)] = Lim f(x). Lim g(x)
X Xo
Exemplos:
X Xo X Xo
Lim (2x2) = Lim 2 . Lim x2
X 2 X 2 X 2
= 2. 22 = 8
Limite do produto](https://image.slidesharecdn.com/apresentaolimite-230529151742-b11e17d6/85/APRESENTACAO-LIMITE-ppt-12-320.jpg)