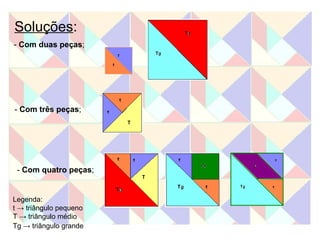
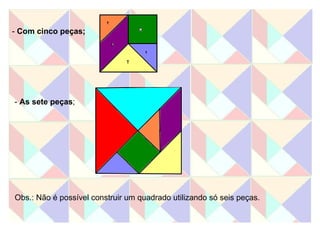
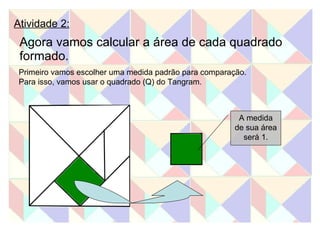
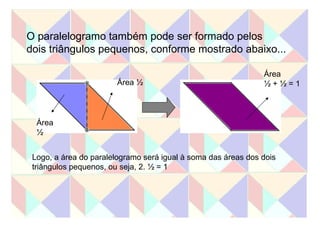
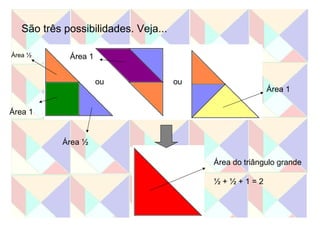
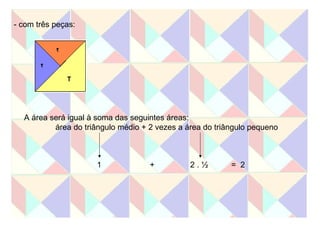
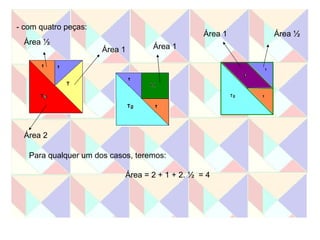
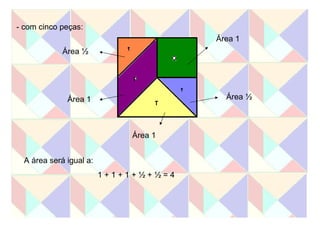
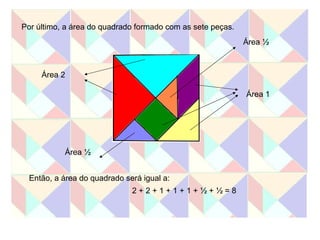
Este documento apresenta duas atividades com o Tangram. A primeira pede para formar oito quadrados usando diferentes números de peças e calcular a área de cada um. A segunda calcula a área de cada peça do Tangram e usa essas áreas para calcular a área dos quadrados formados na primeira atividade.

1. Atividade com o Tangram Atividade 1 : Primeiramente, com as peças do Tangram, vamos formar oito quadrados diferentes, usando: - só duas peças; - só três peças; - só quatro peças; - só cinco peças; - as sete peças. Obs.: Em alguma opção, você conseguirá quadrados formados por figuras diferentes.

2. Soluções : - Com duas peças ; - Com três peças ; - Com quatro peças ; Legenda: t -> triângulo pequeno T -> triângulo médio Tg -> triângulo grande

3. - Com cinco peças; - As sete peças ; Obs.: Não é possível construir um quadrado utilizando só seis peças.

4. Agora vamos calcular a área de cada quadrado formado. Atividade 2: Primeiro vamos escolher uma medida padrão para comparação. Para isso, vamos usar o quadrado (Q) do Tangram. A medida de sua área será 1.

5. Considerando a área do quadrado Q, vamos calcular as áreas das demais peças do Tangram. 1 ª Questão: Quais peças do jogo podemos usar para formar o quadrado Q?

6. Veja... Os dois triângulos pequenos formam o quadrado Q. Como a área do quadrado é 1, a área de cada triângulo pequeno será igual a ½.

7. 2 ª Questão: E para formar o triângulo médio? E o paralelogramo?

8. Repare que o triângulo médio pode ser formado pelos dois triângulos pequenos. Logo, a área do triângulo médio será igual à soma das áreas dos dois triângulos pequenos, ou seja, 2. ½ = 1. Área ½ Área ½ Área ½ + ½ = 1

9. O paralelogramo também pode ser formado pelos dois triângulos pequenos, conforme mostrado abaixo... Logo, a área do paralelogramo será igual à soma das áreas dos dois triângulos pequenos, ou seja, 2. ½ = 1 Área ½ Área ½ Área ½ + ½ = 1

10. 3ª Questão: E para formar o triângulo grande?

11. São três possibilidades. Veja... ou ou Área ½ Área ½ Área 1 Área 1 Área 1 Área do triângulo grande ½ + ½ + 1 = 2

12. Calculadas as áreas de todas as peças que formam o Tangram, vamos partir para o cálculo da área dos quadrados formados. - com duas peças: A área será igual à área do quadrado Q do Tangram, conforme calculado anteriormente, ou seja, a área será igual a 1. A área será igual a duas vezes o valor da área do triângulo grande, de área igual a 2. Logo, a área será igual a 4.

13. - com três peças: A área será igual à soma das seguintes áreas: área do triângulo médio + 2 vezes a área do triângulo pequeno 1 2 . ½ + = 2

14. - com quatro peças: Área ½ Área 1 Área 1 Área 1 Área ½ Área 2 Para qualquer um dos casos, teremos: Área = 2 + 1 + 2. ½ = 4

15. - com cinco peças: Área 1 Área 1 Área 1 Área ½ Área ½ A área será igual a: 1 + 1 + 1 + ½ + ½ = 4

16. Por último, a área do quadrado formado com as sete peças. Área 2 Área 1 Área ½ Área ½ Então, a área do quadrado será igual a: 2 + 2 + 1 + 1 + 1 + ½ + ½ = 8