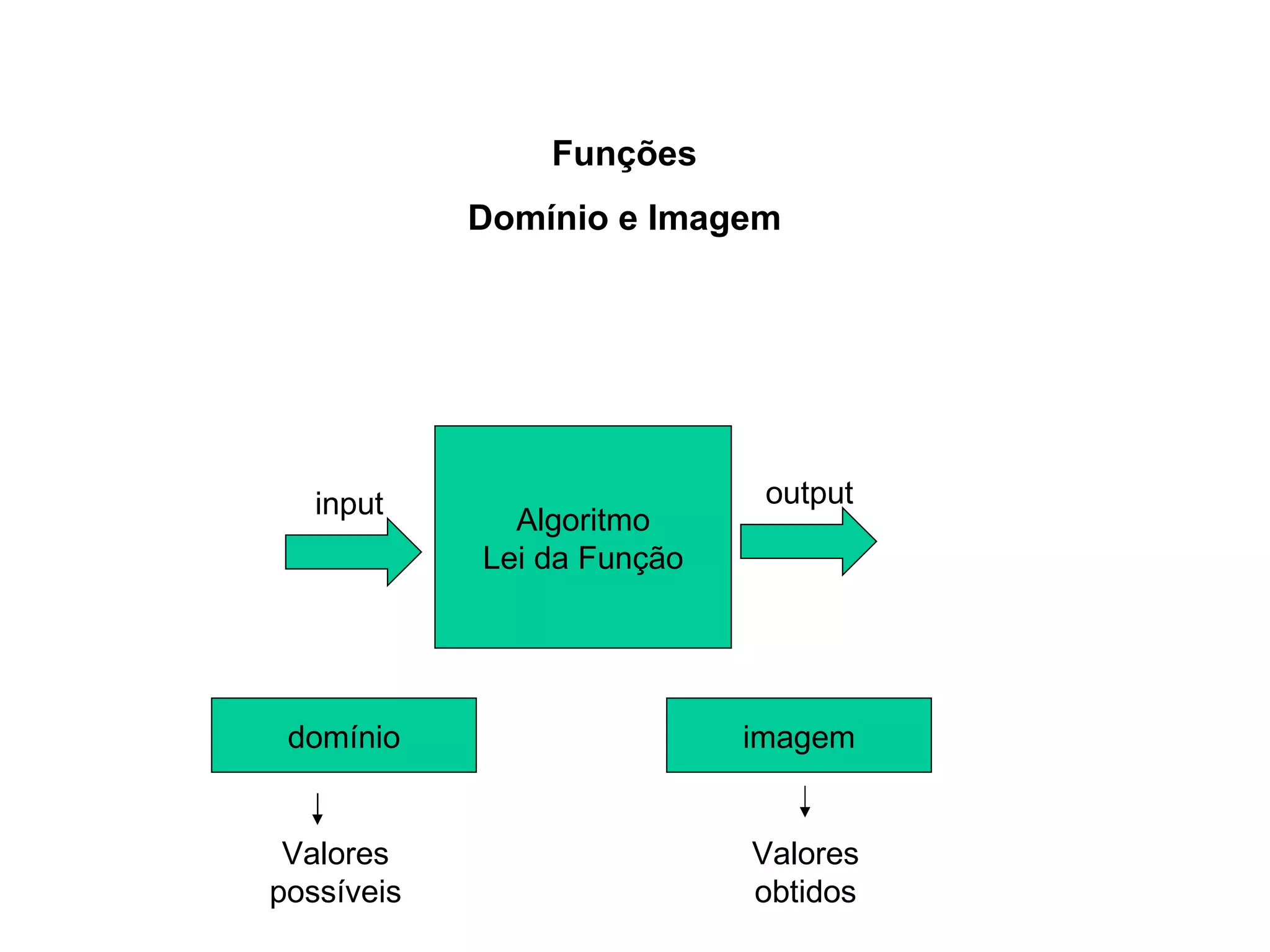
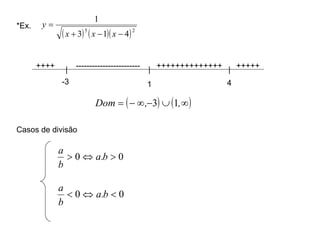
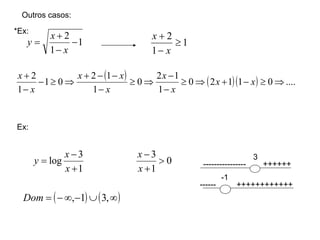
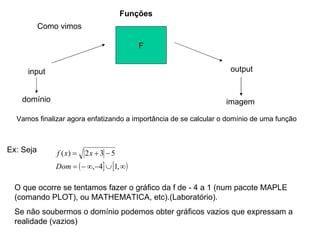
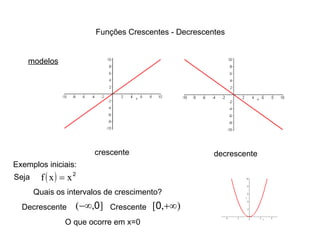
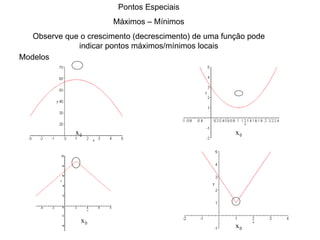
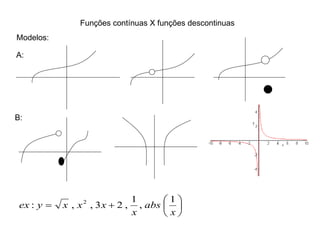
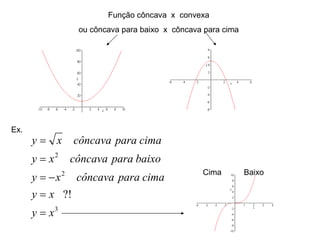
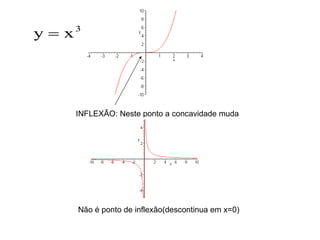
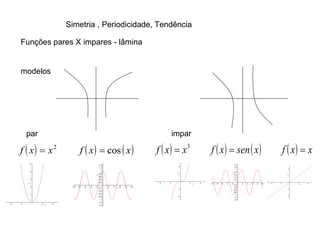
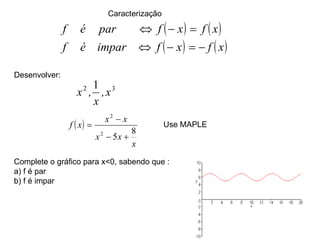
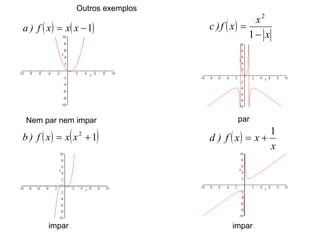
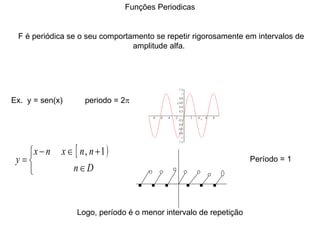
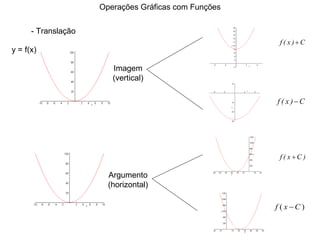
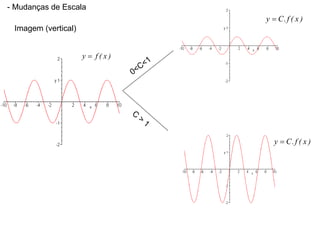
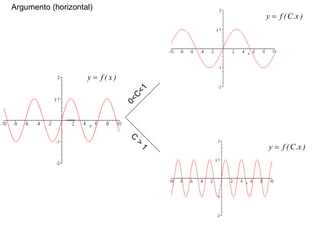
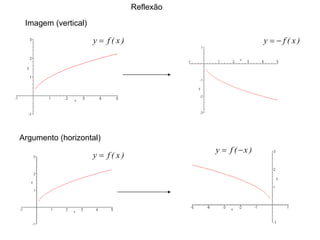
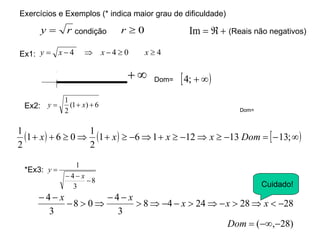
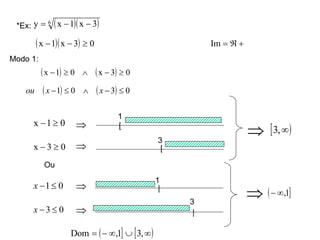
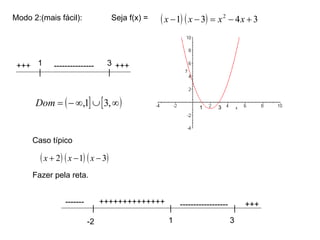
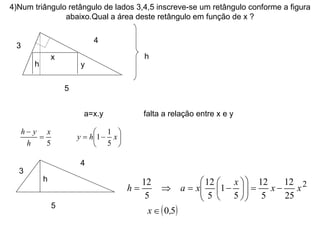
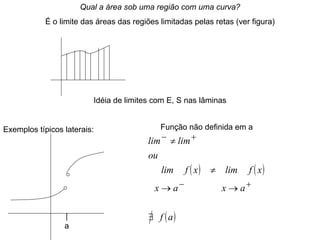
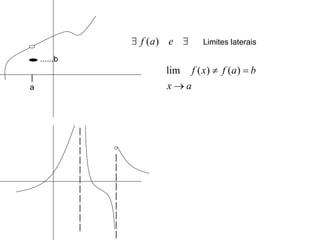
1) O documento discute conceitos fundamentais de funções, incluindo domínio, imagem, leis de funções, gráficos de funções crescentes/decrescentes, pontos especiais, simetria e periodicidade. 2) Apresenta exemplos de modelagem matemática de situações reais usando funções e analisando seus domínios e gráficos. 3) Discutem limites de sequências e como a noção de limite é essencial para o cálculo.

1. Funções Domínio e Imagem Algoritmo Lei da Função input output domínio imagem Valores possíveis Valores obtidos

2. Ex1: 4 Ex2: *Ex3: Cuidado! Exercícios e Exemplos (* indica maior grau de dificuldade) (Reais não negativos) condição Dom= Dom=

3. Leis de Podem ser usadas para simplificar cálculos então

4. *Ex: Modo 1: Ou [ 1 [ 3 | 1 | 3

5. Modo 2:(mais fácil): Seja f(x) = | | 1 3 --------------- +++ +++ Caso típico Fazer pela reta. | | | -2 1 3 ++++++++++++++ ------------------ +++ ------- 1 3

6. *Ex. | | | ------------------------ ++++++++++++++ +++++ ++++ -3 1 4 Casos de divisão

7. Outros casos: *Ex: Ex: 3 -1 ++++++ ++++++++++++ ---------------- ------

8. Outros exemplos: Livro J. Stewart pag. 23 (1.1) – Ex. 23 a 40 .

9. Definição – Valor absoluto a para |a|= -a para |a| = max {-a,a} | | | distância -3 5 distância 0 |-3| = 3 |5| = 5 Obs. ou

10. Exercícios de valor absoluto Ex1. Ex2. Ex3. *Ex4. Ex5. Função BATMAN condição

11. Outros:Desafios 1)Domínio de 2)Determinar x tais que

12. Funções F input output domínio imagem Vamos finalizar agora enfatizando a importância de se calcular o domínio de uma função Ex: Seja O que ocorre se tentamos fazer o gráfico da f de - 4 a 1 (num pacote MAPLE (comando PLOT), ou MATHEMATICA, etc).(Laboratório). Se não soubermos o domínio podemos obter gráficos vazios que expressam a realidade (vazios) Como vimos

13. Funções Crescentes - Decrescentes modelos crescente decrescente Exemplos iniciais: Seja Quais os intervalos de crescimento? Crescente Decrescente O que ocorre em x=0

14. O mesmo para Crescente Decrescente

15. Pontos Especiais Máximos – Mínimos Observe que o crescimento (decrescimento) de uma função pode indicar pontos máximos/mínimos locais Modelos

16. Funções contínuas X funções descontinuas Modelos: A: B:

17. Função côncava x convexa ou côncava para baixo x côncava para cima Ex. Cima Baixo

18. INFLEXÃO: Neste ponto a concavidade muda Não é ponto de inflexão(descontinua em x=0)

19. Simetria , Periodicidade, Tendência Funções pares X impares - lâmina modelos par impar

20. Caracterização Desenvolver: Complete o gráfico para x<0, sabendo que : a) f é par b) f é impar Use MAPLE

21. Outros exemplos Nem par nem impar impar par impar

22. Funções Periodicas F é periódica se o seu comportamento se repetir rigorosamente em intervalos de amplitude alfa. Ex. y = sen(x) periodo = 2  Período = 1 Logo, período é o menor intervalo de repetição

23. AULA Modelagem e análise de funções De uma forma simples: “ Qualquer descrição matemática do mundo real é um modelo” Manipulando um modelo esperamos entender algo da realidade. Linguagem matemática 1) Uma caixa sem tampa é feita a partir de uma folha retangular medindo 12 x 20 cm e cortando-se nos cantos quadrados de lados x. Expresse: a) volume da caixa em função de x b) a superfície da caixa em função de x c) analise o domínio, o gráfico, da função obtida.

24. x 12 20 2)expresse a área de uma janela com o formato abaixo em função do raio x, dado o perímetro de 15 metros l l | x x 3)Expresse o volume de água contido no tanque abaixo em função da altura h h 20 10 Qual a relação entre r e h? r

25. 4)Num triângulo retângulo de lados 3,4,5 inscreve-se um retângulo conforme a figura abaixo.Qual a área deste retângulo em função de x ? 3 4 5 x y h a=x.y falta a relação entre x e y h 3 4 5 h

26. Operações Gráficas com Funções - Translação y = f(x) Imagem (vertical) Argumento (horizontal)

27. - Mudanças de Escala Imagem (vertical) 0<C<1 C > 1

28. Argumento (horizontal) 0<C<1 C > 1

29. Reflexão Imagem (vertical) Argumento (horizontal)

30. Exemplos:Obtenha as funções pedidas a partir da função base e indique que transformação foi realizada.

31. Limites limite de seqüências transparências A idéia de limites Podemos dizer que : Sem a idéia de limites não existiria cálculo. O que é a velocidade instantânea? É o limite das velocidades médias. O que é declividade de uma curva? É o limite das declividades das secantes. O que é o comprimento de uma curva? É o limite co comprimento dos polígonos inscritos O que é a soma de uma série infinita? É o limite das somas dos termos finitos

32. Qual a área sob uma região com uma curva? É o limite das áreas das regiões limitadas pelas retas (ver figura) Idéia de limites com E, S nas lâminas Exemplos típicos laterais: | a Função não definida em a

33. | a | | | | | | | | | | | | | | | | | | | | Limites laterais ......b

34. Usando a idéia de continuidade Vemos que é possível calcular em todo domínio, quando polinômio, por exemplo, Exemplos gráficos:

35. Usando MAPLE para determinar domínios Vamos começar pela última função Usando o comando Solve ; temos como solução Real Range , Real Range Verifique o domínio de todas as funções que enfocamos e teste também algumas mais complicadas, como: