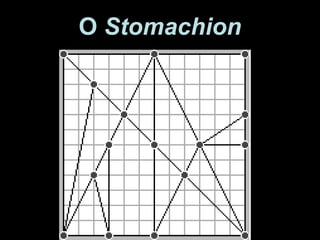
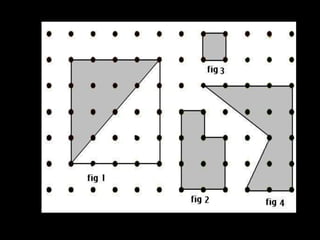
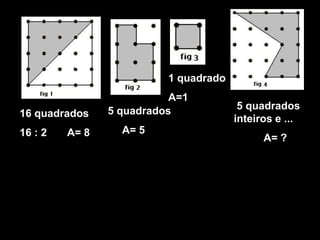
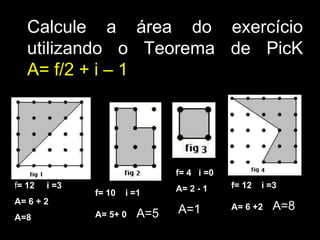
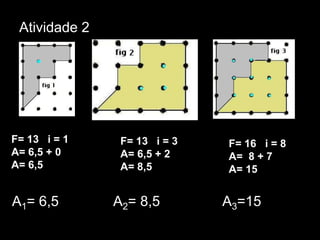
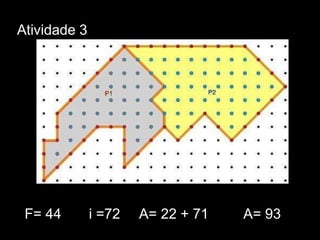
O documento descreve o Stomachion, um quebra-cabeça geométrico atribuído a Arquimedes, e o Teorema de Pick, que permite calcular a área de polígonos simples contando os pontos de fronteira e interiores. O documento apresenta exemplos de aplicação do Teorema de Pick para calcular áreas de vários polígonos.

2. ORGANIZAÇÃOLudovina Morais de Oliveira

3. O Stomachion

4. A invenção de um dos mais antigos quebra-cabeças geométrico que se conhece é atribuída a Arquimedes,sábio grego que viveu em Siracusa, Sicília, no séc. III a.C. O Stomachion é constituído por um conjunto de 14 peças planas (originalmente em marfim) de várias formas poligonais com duas características fundamentais:

5. podem unir-se de modo a formar um quadrado; a área de cada peça é comensurável com a área do quadrado anterior. O que significa comensurável? Significa que o quociente entre a área de cada peça e a área do quadrado total é um número racional.Teorema de PickGeorg Alexander Pick (1859-1942)

6. Este teorema foi descoberto pela primeira vez pelo matemático Georg Alexander Pick em 1899; O teorema de Pick só é válido para figuras simples, isto é para figuras em que os lados não se intersectem a não ser, eventualmente, nos vértices. O teorema é usado, por exemplo, na indústria florestal, para determinar a área de uma região em função do número de árvores (regularmente espaçadas).

7. O cálculo de áreas de polígonos nem sempre é uma tarefa fácil, pela variedade de formas que podem assumir. Não é fácil, por exemplo, calcular a área do polígono apresentado a seguir:

9. Este polígono é de fato complicado! No entanto, tem a particularidade de ter os seus vértices sobre um reticulado de pontos no plano, constituído por pontos de coordenadas inteiras.Muitas vezes recorremos a processos de dissecção do polígono ou de subtração de áreas. Todos estes processos envolvem a área como um conceito bidimensional. O novo método que apresentamos permite o cálculo da área pela simples contagem de pontos.

10. Introduzindo o Teorema de Pick

11. Usando o quadrado como unidade de medida, encontre a área das figuras da atividade 1:1

12. Calcule a área das figuras,

13. 1 quadradoA=1 5 quadrados inteiros e ...A= ?5 quadrados A= 516 quadrados16 : 2 A= 8

14. Teorema de PickDado um polígono simples P, sejam f o número de pontos de fronteira, i o número de pontos interiores. Então a área A(P) desse polígono é dada pela expressão seguinte A(P) = f + i - 1

15. Calcule a área do exercício utilizando o Teorema de PicK A= f/2 + i – 1f= 4 i =0A= 2 - 1 A=1f= 12 i =3A= 6 +2 A=8f= 12 i =3A= 6 + 2 A=8f= 10 i =1A= 5+ 0 A=5

16. Atividade 2F= 13 i = 1A= 6,5 + 0 A= 6,5F= 13 i = 3A= 6,5 + 2A= 8,5F= 16 i = 8A= 8 + 7A= 15A1= 6,5 A2= 8,5 A3=15

17. Atividade 3F= 44 i =72 A= 22 + 71 A= 93

18. DESAFIO

20. f=125 i =212A= 125/2 + 212 -1A= 62,5 + 211 = 273,5

21. Fontes de pesquisa:http://matemateca.incubadora.fapesp.br/portal/matemateca/exposicao/pick/http://cmup.fc.up.pt/cmup/pick/index.htmlhttp://www.mat.uc.pt/~jaimecs/matelem/stomachion.html