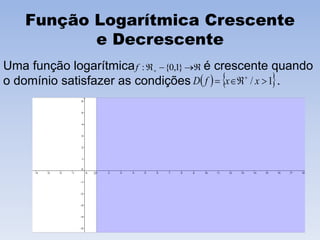
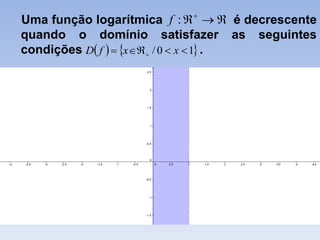
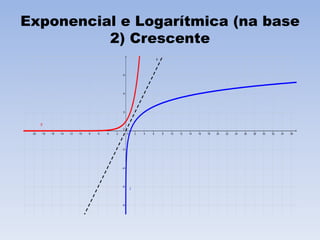
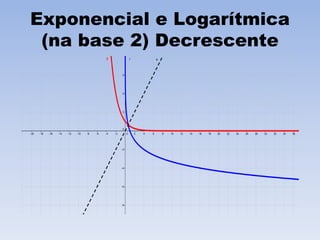
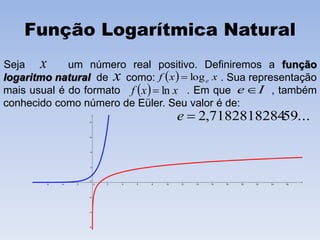
O documento discute funções logarítmicas, definindo-as como a função inversa da função exponencial e descrevendo seu domínio e imagem. Também explica quando funções logarítmicas são crescentes ou decrescentes e fornece exemplos de aplicações como juros contínuos, desintegração radioativa e resfriamento de corpos.

1. Funções Logarítmicas
Professor: Caio Lopes Rodrigues
Turmas: M05 e M09

2. Definição
Se é um número qualquer positivo diferente de 1 e de 0, a
função exponencial de base é injetora e,
portanto, possui uma função inversa. Essa função é
denominada função logarítmica de base . Ou seja:
A função logarítmica de base é a função , é
a função inversa da função exponencial de base :
.
x
axf )( a
a
a
a xxf alog)( 
a
x
axf )(

3. Domínio e Imagem da
Função Logarítmica
O domínio da função é:
ou seja, é a imagem da função .
A imagem da função é:
ou seja, é o domínio da função .
xxf alog)( 
  }0/{ *
  xxfD
x
axg )(
xxf alog)( 
})(/)({)Im(  xfxff
x
axg )(

4. Função Logarítmica Crescente
e Decrescente
Uma função logarítmica é crescente quando
o domínio satisfazer as condições .
 }1,0{:f
   1/  
xxfD

5. Uma função logarítmica é decrescente
quando o domínio satisfazer as seguintes
condições .

:f
   10/   xxfD

6. Gráficos das Funções
Exponenciais e
Logarítmicas Crescentes
e Decrescentes

7. Exponencial e Logarítmica (na base
2) Crescente

8. Exponencial e Logarítmica
(na base 2) Decrescente

9. Função Logarítmica Natural
Seja um número real positivo. Definiremos a função
logaritmo natural de como: . Sua representação
mais usual é do formato . Em que , também
conhecido como número de Eüler. Seu valor é de:
x
x   xxf elog
  xxf ln Ie
...597182818284,2e

10. Aplicações
•Calcular Juros Contínuos: usa-se a seguinte fórmula:
Em que é o capital após meses, é o capital
aplicado, e é a taxa de juros, em que é a taxa
de juros em porcentagem.
t
t
ctc 







1)(
)(tc t c
100
k
 k

11. •Desintegração Radioativa: Cuja fórmula do
problema é dada por:
Em que é a massa desintegrada do corpo
após t segundos é a massa inicial do corpo
radioativo, e é a taxa de desintegração que
muda de corpo radioativo para corpo radioativo.
t
eMtM 
 0)(
)(tM
0M


12. • O Método do Carbono 14: Cuja fórmula é
dada por
Observemos que a função é a mesmo da Desintegração
radioativa, contudo será o valor da taxa de
desintegração do Carbono 14 - .
t
eMtM 
 0)(
 14
C

13. • Tempo de Resfriamento de um Corpo:
A função que calcula o tempo de resfriamento é
dada por
Também conhecida como A Lei de Resfriamento
de Newton.
 








0)(
ln
T
tT
t


14. Obrigado pela Vossa
Atenção!!!