O documento apresenta regras e exemplos de multiplicação e divisão de números inteiros, incluindo o sinal do resultado dependendo do número de fatores negativos na multiplicação. Ele também fornece uma série de exercícios resolvidos de multiplicação, divisão, soma e subtração de inteiros.






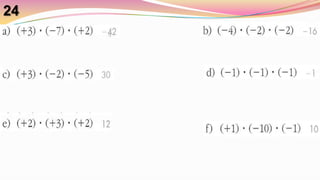



![9 – [ (–14 ) – ( –24 ) ] 9 – [ – 14 + 24 ]9 – [ + 10 ]9 – 10 – 1](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-11-320.jpg)
![(– 6) + { 2 . [– 3 + ( + 8 )]}– 6 + { 2 . [– 3 + 8]}– 6 + { 2 . 5}– 6 + 104](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-12-320.jpg)


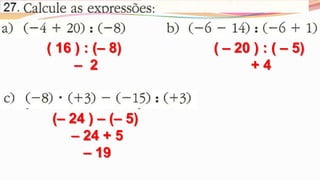
![[ – 8 + ( + 12) ] : ( – 2 ) [ – 8 + 12 ] : ( – 2 )[ + 4 ] : ( – 2)– 2(– 8 + 3 ) : [ – 3 . ( + 1) + 8]( – 5) : [ – 3 + 8]( – 5) : [ + 5] – 1](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-16-320.jpg)
![– 20 : { – 6 + [(+ 6) : (+ 2)] – 2} – 20 : { – 6 + [+ 3] – 2} – 20 : { – 6 + 3 – 2}– 20 : { – 5}+ 4](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-17-320.jpg)
![10 – { – 6 + [(+ 4) – 8]}10 – { – 6 + [– 4]}10 – { – 6 – 4}10 – {– 10}10 + 1020](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-18-320.jpg)
![[ – 20 + ( – 8 )] : [ 1 + ( + 6 )][ – 20 – 8 ] : [ 1 + 6 ][ – 28 ] : [ 7 ]– 4](https://image.slidesharecdn.com/multiplicaoedivisodeinteiros-110327170156-phpapp01/85/Multiplicacao-e-divisao-de-inteiros-19-320.jpg)
