O documento discute conceitos matemáticos básicos como números inteiros, operações com números inteiros (adição, subtração, multiplicação) e suas propriedades. Ele fornece definições formais para os conjuntos de números inteiros e racionais, além de exemplos e exercícios para demonstrar o uso dessas operações.


![3
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
13/02 IOF* 1,00 c)
14/02 Cheque 123,00 d)
15/02 Depósito 150,00 e)
* IOF – Imposto sobre Operações Financeiras.
Cabe a você encontrar o saldo bancário de Cláudia dia a dia.
10- Qual a diferença prevista entre
as temperaturas no Piauí e no Rio
Grande do Sul, num determinado
dia, segundo as informações?
Tempo no Brasil: Instável a ensolarado no Sul.
Mínima prevista -3º no Rio Grande do Sul.
Máxima prevista 37° no Piauí.
RESPOSTAS
1- 153
2- 283
3 - a) x = 200 b) x = 420
4- 14
5- 270
6- a) -20 b) –26
7- a) –28 b) 52 c) 0
8- a) 7 b) –9 c) 4
9- a) – 165,00 b) 35,00
10- (+40 graus)
MULTIPLICAÇÃO DE NÚMEROS INTEIROS
A multiplicação funciona como uma forma simplificada de
uma adição quando os números são repetidos. Poderíamos analisar
tal situação como o fato de estarmos ganhando repetidamente
alguma quantidade, como por exemplo, ganhar 1 objeto por 30
vezes consecutivas, significa ganhar 30 objetos e esta repetição
pode ser indicada por um x, isto é: 1 + 1 + 1 ... + 1 + 1 = 30 x 1 = 30
Se trocarmos o número 1 pelo número 2, obteremos: 2 + 2 + 2
+ ... + 2 + 2 = 30 x 2 = 60
Se trocarmos o número 2 pelo número -2, obteremos: (–2) +
(–2) + ... + (–2) = 30 x (2) = –60
Observamos que a multiplicação é um caso particular da
adição onde os valores são repetidos.
Na multiplicação o produto dos números a e b, pode ser
indicado por a x b, a . b ou ainda ab sem nenhum sinal entre as
letras.
Para realizar a multiplicação de números inteiros, devemos
obedecer à seguinte regra de sinais:
(+1) × (+1) = (+1)
(+1) × (-1) = (-1)
(-1) × (+1) = (-1)
(-1) × (-1) = (+1)
Com o uso das regras acima, podemos concluir que:
Sinais dos números Resultado do produto
iguais positivo
diferentes negativo
Propriedades da multiplicação de números inteiros: O
conjunto Z é fechado para a multiplicação, isto é, a multiplicação
de dois números inteiros ainda é um número inteiro.
Associativa: Para todos a,b,c em Z:
a x (b x c) = (a x b) x c
2 x (3 x 7) = (2 x 3) x 7
Comutativa: Para todos a,b em Z:
a x b = b x a
3 x 7 = 7 x 3
Elemento neutro: Existe 1 em Z, que multiplicado por todo z
em Z, proporciona o próprio z, isto é:
z x 1 = z
7 x 1 = 7
Elemento inverso: Para todo inteiro z diferente de zero, existe
um inverso z–1
=1/z em Z, tal que
z x z–1
= z x (1/z) = 1
9 x 9–1
= 9 x (1/9) = 1
Distributiva: Para todos a,b,c em Z:
a x (b + c) = (a x b) + (a x c)
3 x (4+5) = (3 x 4) + (3 x 5)
EXERCÍCIOS
Quando numa expressão aparecem parênteses ( ), colchetes
[ ] e chaves { }, resolvem-se primeiro as operações contidas nos
parênteses, depois as operações contidas nos colchetes e por último
as operações contidas nas chaves.
1- Calcule o valor das seguintes expressões numéricas:
a) –5 + (–3) . (+8)
b) (–6) . (+5) – (–4) . (+3)
c) (–5 + 1) . (–8 + 2)
d) 6 – (–6 + 4) . (–5 + 9)
e) (–3) . (–4) + (–6) . (+5)
f) 12 – (–2) . (+3) + (–4) . (–5)
g) 9 – [(–2) . (+7) – (–8) . (+3)]
h) (–2) . (+3) + {2 . [–3 + (–2) . (–4)]}
2- Calcule o valor numérico das expressões:
a) 2x – y, sendo x = –3 e y = –5
b) 4x – 2y + 5z, sendo x = –1, y = –6 e z = +5
c) 4ab + 5a, sendo a = 7 e b = –8
d) 6xy – 5y, sendo x = +4 e y = –1
e) 5a – 3ab + 7b, para a = –3 e b = +2
f) 2ab – 5abc, para a = 2, b = 3 e c = –1
3- Use a propriedade distributiva da multiplicação para
calcular –5 . (–8 + 5).
4- Sem realizar a operação, determine o número inteiro que
devemos colocar no lugar do número x para que se tenha:](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-3-320.jpg)

![5
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
4- Sabendo que A = (–46 – 18) : (59 – 43), determine o valor
de A.
5- Sendo x = (–82 + 34 – 6) e y = (–9) . (51 – 53), qual é o
valor de x : y?
6- Qual é o valor de B, se B = (–6 + 2 + 4 – 8 + 8) : (+138)?
7- Sabendo que a = (–25 + 18 – 72 + 49) : (–15) e b = (+24):
(81 – 93 + 17 – 42 + 25), responda:
a) Qual o valor de a?
b) Qual o valor de b
c) Qual o valor do produto a . b?
8- Qual é o número inteiro que dividido por –8 resulta +12?
9- Nicolau pensou em um número que multiplicado por (-25)
tem como resultado (+150). Qual foi o número em que Nicolau
pensou?
10- Adicionando –846 a um número inteiro e multiplicando a
soma por –3, obtém-se +324. Que número é esse?
RESPOSTAS
1) a) 0 b) – 13 c) 9 d) – 27 e) 35 f) – 60 g) – 36 h) – 40
i) – 12
2) d, e
3) a) + 7 b) – 36 c) – 7 d) + 156 e) – 4 185 f) + 432
4) -4
5) -3
6) 0
7) a) 2 b) – 2 c) – 4
8) -96
9) -6
10) +738
POTENCIAÇÃO DE NÚMEROS INTEIROS
Apotência an
do número inteiro a, é definida como um produto
de n fatores iguais. O número a é denominado a base e o número
n é o expoente.
an
= a × a × a × a × ... × a
a é multiplicado por a n vezes
Exemplos:
33
= (3) x (3) x (3) = 27
(-5)5
= (-5) x (-5) x (-5) x (-5) x (-5) = -3125
(-7)² = (-7) x (-7) = 49
(+9)² = (+9) x (+9) = 81
Toda potência de base positiva é um número inteiro
positivo.
Exemplo: (+3)2
= (+3) . (+3) = +9
Toda potência de base negativa e expoente par é um
número inteiro positivo.
Exemplo: (– 8)2
= (–8) . (–8) = +64
Toda potência de base negativa e expoente ímpar é
um número inteiro negativo.
Exemplo: (–5)3
= (–5) . (–5) . (–5) = –125
Propriedades da Potenciação:
Produtos de Potências com bases iguais: Conserva-se a base
e somam-se os expoentes. (–7)3
. (–7)6
= (–7)3+6
= (–7)9
Quocientes de Potências com bases iguais: Conserva-se
a base e subtraem-se os expoentes. (+13)8
: (+13)6
= (+13)8 – 6
=
(+13)2
Potência de Potência: Conserva-se a base e multiplicam-se
os expoentes. [(+4)5
]2
= (+4)5 . 2
= (+4)10
Potência de expoente 1: É sempre igual à base. (+9)1
= +9
(–13)1
= –13
Potência de expoente zero e base diferente de zero: É igual
a 1. Exemplo: (+14)0
= 1 (–35)0
= 1
EXERCÍCIOS
1- Determine a quinta potência de –2.
2- Calcule o valor das seguintes expressões:
a) (–7 + 8 – 4)4
b) (–13 + 92 – 58)0
c) (–15 + 8 + 3 + 4)10
d) (–25 + 39 – 24)3
e) (–65 + 82 – 23)1
f) (–108 + 212 – 103)7
3- Identifique as igualdades verdadeiras:
a) –40
= –1
b) [(+3) + (–2)]5
= (+3)5
+ (–2)5
c) [a2
]5
= a7
d) [(+35) : (–7)]5
= (+35)5
: (–7)5
e) a4
. a3
. b2
= a7
. b2
f) (–1)100
= –1
4- Aplique propriedades de potências de bases iguais e
calcule os valores de:
a) (–1)8
. (–1)3
b) (+10)2
. (+10)3
c) (+12)5
: (+12)4
d) (–20)6
: (–20)6
e) [(+1)3
]6
f) [(–2)3
]0
5- Se A = (–9)2
e B = – (–9)2
, qual é o valor de A . B?
6- Considerando A = (–10)3
e B = – (–10)3
, qual é o valor de
A . B?
7- A letra x representa um número inteiro. A expressão x2 é o
quadrado do valor de x. Qual é o valor da expressão x2
– 2 . x + 1
para x = –1?
8- As letras x e y representam números inteiros, Calcule o
valor da expressão 2 . x – y2
para x = –2 e y = 5.](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-5-320.jpg)






![12
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
2) Escreva o quociente
412
25
16
:
25
16
-
- como uma só
potência.
3) Se x =
8
23
10
- ,como se escreve x5
usando um só
expoente?
4) Utilize as propriedades das potências de bases iguais e
escreva como uma só potência:
a)
36
20
17
.
20
17
-
-
b)
46
4
3
:
4
3
-
-
c)
52
25
13
+
d) [ (– 0,18)3
]5
e)
59
15
43
.
15
43
+
+
f)
59
15
43
.
15
43
+
+
5)Qual é o valor da expressão
+
---
4
3
:
2
1
24
13
3
?
6) Calcule o valor das expressões numéricas:
a) 2
3
2
:
3
2
25
-
-
-
b)
-
-
-
-
36
25
15
28
:
5
7
:
6
1
3
c) ( )
+-+--
6
1
3:52.
3
2 2
d)
-
-+
2
3
:
5
2
.5
10
3
2
e) 25 – [( 3,3 – 0,2 . 1,5 ) – 6,4 : 0,8]2
f)
-+-+
+
-
--- 212
2
1
13
5
1
3
1
.
2
1
3
7) Qual é o valor de 3
21
3
33
-
--
+
?
8) Determine o valor da expressão
2
2
3
1
1
3
-
-
-
-
.
9)Como 27 = 33
, usando expoentes inteiros negativos podemos
escrever 3-3
para representar
27
1
. Procedendo da mesma forma,
como poderíamos escrever
27
1
?
10) Use potências de base 10 e expoentes inteiros negativos
para escrever os seguintes números:
a) 0,0003
b) 0,005
c) 0,00018
d) 0,081
e) – 0,00016
f) –0,000418
RESPOSTAS
1)
10
3
2
+
2)
8
25
16
- 3)
40
23
10
-
4) a) (-17/20)9
b) (-3/4)2
c) (13/25)10
d) (-0,18)15
e) (-719)8
f)
(-4315)14
5) – 3/8
6) a) -62/27 b) -1/12 c) 23/27 d) -11/15 e) 0 f) 13/10
7) 12
8) 1/72
9) 2-4
10) a) 3.10-4
b) 5.10-3
c) 18.10-5
d) 81.10-3
e) -16.10-5
f)
-418.10-6](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-12-320.jpg)
![13
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
EXPRESSÕES NUMÉRICAS
Expressões Algébricas são aquelas que contêm números e
letras.
Ex: 2ax²+bx
Variáveis são as letras das expressões algébricas que
representam um número real e que de princípio não possuem um
valor definido.
Valor numérico de uma expressão algébrica é o número que
obtemos substituindo as variáveis por números e efetuamos suas
operações.
Ex: Sendo x =1 e y = 2, calcule o valor numérico (VN) da
expressão:
x² + y » 1² + 2 =3 Portando o valor numérico da expressão
é 3.
Monômio: os números e letras estão ligados apenas por
produtos.
Ex : 4x
Polinômio: é a soma ou subtração de monômios.
Ex: 4x+2y
Termos semelhantes: são aqueles que possuem partes literais
iguais ( variáveis )
Ex: 2 x³ y² z e 3 x³ y² z » são termos semelhantes pois
possuem a mesma parte literal.
Adição e Subtração de expressões algébricas
Para determinarmos a soma ou subtração de expressões
algébricas, basta somar ou subtrair os termos semelhantes.
Assim: 2 x³ y² z + 3x³ y² z = 5x³ y² z ou 2 x³ y² z - 3x³ y² z
= -x³ y² z
Convém lembrar dos jogos de sinais.
Na expressão ( x³ + 2 y² + 1 ) – ( y ² - 2 ) = x³ +2 y² + 1 – y²
+ 2 = x³ + y² +3
Multiplicação e Divisão de expressões algébricas
Na multiplicação e divisão de expressões algébricas, devemos
usar a propriedade distributiva.
Exemplos:
1) a ( x+y ) = ax + ay
2) (a+b)(x+y) = ax + ay + bx + by
3) x ( x ² + y ) = x³ + xy
»Paramultiplicarmospotênciasdemesmabase,conservamos
a base e somamos os expoentes.
» Na divisão de potências devemos conservar a base e
subtrair os expoentes
Exemplos:
1) 4x² : 2 x = 2 x
2) ( 6 x³ - 8 x ) : 2 x = 3 x² - 4
3)
=
[Resolução]
Para iniciarmos as operações devemos saber o que são termos
semelhantes.
Dizemos que um termo é semelhante do outro quando suas
partes literais são idênticas.
Veja:
► 5x2
e 42x são dois termos, as suas partes literais são x2
e x,
as letras são iguais, mas o expoente não, então esses termos não
são semelhantes.
► 7ab2
e 20ab2
são dois termos, suas partes literais são ab2
e
ab2
, observamos que elas são idênticas, então podemos dizer que
são semelhantes.
Adição e subtração de monômios
Só podemos efetuar a adição e subtração de
monômios entre termos semelhantes. E quando os termos
envolvidos na operação de adição ou subtração não forem
semelhantes, deixamos apenas a operação indicada.
Veja:
Dado os termos 5xy2
, 20xy2
, como os dois termos são
semelhantes eu posso efetuar a adição e a subtração deles.
• 5xy2
+ 20xy2
devemos somar apenas os coeficientes e
conservar a parte literal.
25 xy2
• 5xy2
- 20xy2
devemos subtrair apenas os coeficientes e
conservar a parte literal.
- 15 xy2
Veja alguns exemplos:
• x2
- 2x2
+ x2
como os coeficientes são frações devemos tirar
o mmc de 6 e 9.
3x2
- 4 x2
+ 18 x2
18
17x2
18
• 4x2
+ 12y3
– 7y3
– 5x2
devemos primeiro unir os termos
semelhantes.12y3
–7y3
+4x2
–5x2
agoraefetuamosasomaeasubtração.
5y3
– x2
como os dois termos restantes não são semelhantes,
devemos deixar apenas indicado à operação dos monômios.
• Reduza os termos semelhantes na expressão 4x2
– 5x -3x +
2x2
. Depois calcule o seu valor numérico da expressão. 4x2
– 5x -
3x + 2x2
reduzindo os termos semelhantes. 4x2
+ 2x2
– 5x - 3x](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-13-320.jpg)
![14
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
6x2
- 8x os termos estão reduzidos, agora vamos achar o valor
numérico dessa expressão.
Para calcularmos o valor numérico de uma expressão devemos
ter o valor de sua incógnita, que no caso do exercício é a letra x.
Vamos supor que x = - 2, então substituindo no lugar do x o
-2 termos:
6x2
- 8x
6 . (-2)2
– 8 . (-2) =
6 . 4 + 16 =
24 + 16
40
Multiplicação de monômios
Paramultiplicarmosmonômiosnãoénecessárioqueelessejam
semelhantes, basta multiplicarmos coeficiente com coeficiente e
parte literal com parte literal. Sendo que quando multiplicamos
as partes literais devemos usar a propriedade da potência que diz:
am
. an
= am + n
(bases iguais na multiplicação repetimos a base e
somamos os expoentes).
(3a2
b) . (- 5ab3
) na multiplicação dos dois monômios, devemos
multiplicar os coeficientes 3 . (-5) e na parte literal multiplicamos
as que têm mesma base para que possamos usar a propriedade am
. an
= am + n
.
3 . ( - 5) . a2
. a . b . b3
-15 a2 +1
b1 + 3
-15 a3
b4
DIVISÃO DE MONÔMIOS
Para dividirmos os monômios não é necessário que eles sejam
semelhantes, basta dividirmos coeficiente com coeficiente e parte
literal com parte literal. Sendo que quando dividirmos as partes
literais devemos usar a propriedade da potência que diz: am
: an
= am - n
(bases iguais na divisão repetimos a base e diminuímos os
expoentes), sendo que a ≠ 0.
(-20x2
y3
) : (- 4xy3
) na divisão dos dois monômios, devemos
dividir os coeficientes -20 e - 4 e na parte literal dividirmos as que
têm mesma base para que possamos usar a propriedade am : an
=
am – n
.
-20 : (– 4) . x2
: x . y3
: y3
5 x2 – 1
y3 – 3
5x1
y0
5x
Potenciação de monômios
Na potenciação de monômios devemos novamente utilizar
uma propriedade da potenciação:
(I) (a . b)m
= am
. bm
(II) (am)n
= am . n
Veja alguns exemplos:
(-5x2
b6
)2
aplicando a propriedade
(I). (-5)2
. (x2
)2
. (b6
)2
aplicando a propriedade
(II) 25 . x4
. b12
25x4
b12
BINÔMIO
Denomina-se Binômio de Newton , a todo binômio da forma
(a + b)n
, sendo n um número natural .
Exemplo:
B = (3x - 2y)4
( onde a = 3x, b = -2y e n = 4 [grau do binômio]
).
Exemplos de desenvolvimento de binômios de Newton :
a) (a + b)2
= a2
+ 2ab + b2
b) (a + b)3
= a3
+ 3 a2
b + 3ab2
+ b3
c) (a + b)4
= a4
+ 4 a3
b + 6 a2
b2
+ 4ab3
+ b4
d) (a + b)5
= a5
+ 5 a4
b + 10 a3
b2
+ 10 a2
b3
+ 5ab4
+ b5
Nota:
Não é necessário memorizar as fórmulas acima, já que elas
possuem uma lei de formação bem definida, senão vejamos:
Vamos tomar, por exemplo, o item (d) acima:
Observe que o expoente do primeiro e últimos termos são
iguais ao expoente do binômio, ou seja, igual a 5.
A partir do segundo termo, os coeficientes podem ser obtidos
a partir da seguinte regra prática de fácil memorização:
Multiplicamos o coeficiente de a pelo seu expoente e dividimos
o resultado pela ordem do termo. O resultado será o coeficiente do
próximo termo. Assim por exemplo, para obter o coeficiente do
terceiro termo do item (d) acima teríamos:
5.4 = 20; agora dividimos 20 pela ordem do termo anterior (2
por se tratar do segundo termo) 20:2 = 10 que é o coeficiente do
terceiro termo procurado.
Observe que os expoentes da variável a decrescem de n até 0
e os expoentes de b crescem de 0 até n. Assim o terceiro termo é
10 a3
b2
(observe que o expoente de a decresceu de 4 para 3 e o de
b cresceu de 1 para 2).
Usando a regra prática acima, o desenvolvimento do binômio
de Newton (a + b)7
será:
(a + b)7
= a7
+ 7 a6
b + 21 a5
b2
+ 35 a4
b3
+ 35 a3
b4
+ 21 a2
b5
+
7 ab6
+ b7
Como obtivemos, por exemplo, o coeficiente do 6º termo (21
a2
b5
) ?
Pela regra: coeficiente do termo anterior = 35. Multiplicamos
35 pelo expoente de a que é igual a 3 e dividimos o resultado pela
ordem do termo que é 5.
Então, 35 . 3 = 105 e dividindo por 5 (ordem do termo anterior)
vem 105:5 = 21, que é o coeficiente do sexto termo, conforme se
vê acima.
Observações:
1) o desenvolvimento do binômio (a + b)n
é um polinômio.
2) o desenvolvimento de (a + b)n
possui n + 1 termos .
3) os coeficientes dos termos eqüidistantes dos extremos , no
desenvolvimento De (a + b)n
são iguais .](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-14-320.jpg)
![15
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
4) a soma dos coeficientes de (a + b)n
é igual a 2n
.
Fórmula do termo geral de um Binômio de Newton
Um termo genérico Tp+1
do desenvolvimento de (a+b)n
, sendo
p um número natural, é dado por
onde
é denominado Número Binomial e Cn.p
é o número de
combinações simples de n elementos, agrupados p a p, ou seja, o
número de combinações simples de n elementos de taxa p.
Este número é também conhecido como Número
Combinatório.
EXERCÍCIOS
1 - Determine o 7º termo do binômio (2x + 1)9
, desenvolvido
segundo as potências decrescentes de x.
Solução:
Vamos aplicar a fórmula do termo geral de (a + b)n
, onde a
= 2x , b = 1 e n = 9. Como queremos o sétimo termo, fazemos p
= 6 na fórmula do termo geral e efetuamos os cálculos indicados.
Temos então:
T6+1
= T7
= C9,6
. (2x)9-6
. (1)6
= 9! /[(9-6)! . 6!] . (2x)3
. 1 =
9.8.7.6! / 3.2.1.6! . 8x3
= 84.8x3
= 672x3
. Portanto o sétimo termo
procurado é 672x3
.
2 - Qual o termo médio do desenvolvimento de (2x + 3y)8
?
Solução:
Temos a = 2x , b = 3y e n = 8. Sabemos que o desenvolvimento
do binômio terá 9 Termos, porque n = 8. Ora sendo T1 T2 T3 T4
T5 T6 T7 T8 T9 os termos do desenvolvimento do binômio, o
termo do meio (termo médio) será o T5 (quinto termo).
Logo, o nosso problema resume-se ao cálculo do T5
. Para isto,
basta fazer p = 4 na fórmula do termo geral e efetuar os cálculos
decorrentes. Teremos:T4+1
= T5
= C8,4
. (2x)8-4
. (3y)4
= 8! / [(8-4)! .
4!] . (2x)4
. (3y)4
= 8.7.6.5.4! / (4! . 4.3.2.1) . 16x4
.81y4
Fazendo as contas vem:
T5
= 70.16.81.x4
. y4
= 90720x4
y4
, que é o termo médio
procurado.
3 - Desenvolvendo o binômio (2x - 3y)3n
, obtemos um
polinômio de 16 termos. Qual o valor de n?
Solução:
Ora, se o desenvolvimento do binômio possui 16 termos,
então o expoente do binômio é igual a 15.
Logo, 3n = 15 de onde conclui-se que n = 5.
4 - Determine o termo independente de x no desenvolvimento
de (x + 1/x )6
.
Solução:
Sabemos que o termo independente de x é aquele que não
depende de x, ou seja, aquele que não possui x.
Temos no problema dado: a = x , b = 1/x e n = 6.
Pela fórmula do termo geral, podemos escrever:
Tp+1
= C6,p
. x6-p
. (1/x)p
= C6,p
. x6-p
. x-p
= C6,p
. x6-2p
.
Ora, para que o termo seja independente de x, o expoente
desta variável deve ser zero, pois x0
= 1. Logo, fazendo 6 - 2p
= 0, obtemos p=3. Substituindo então p por 6, teremos o termo
procurado. Temos então:
T3+1
= T4
= C6,3
. x0
= C6,3
= 6! /[(6-3)! . 3! ] = 6.5.4.3! / 3!.3.2.1
= 20.
Logo, o termo independente de x é o T4
(quarto termo) que é
igual a 20.
EXERCÍCIOS
1) Qual é o termo em x5
no desenvolvimento de (x + 3)8
?
2) Determine a soma dos coeficientes do desenvolvimento de
(x - 3y)7
.
3) Qual é o valor do produto dos coeficientes do 2o. e do
penúltimo termo do desenvolvimento de (x - 1)80
?
4) FGV-SP - Desenvolvendo-se a expressão [(x + 1/x) . (x -
1/x)]6
, obtém-se como termo independente de x o valor:
a) 10
b) -10
c) 20
d) -20
e) 36
5) UF. VIÇOSA-Asoma dos coeficientes do desenvolvimento
de (2x + 3y)m
é 625. O valor de m é:
a) 5
b) 6
c)10
d) 3
e) 4
6)MACK-SP-Os3primeiroscoeficientesnodesenvolvimento
de (x2
+ 1/(2x))n
estão em progressão aritmética.O valor de n é:
a) 4
b) 6
c) 8
d) 10
e) 12
7) No desenvolvimento de (3x + 13)n
há 13 termos. A soma
dos coeficientes destes termos é igual a:
8) UFBA-92 - Sabendo-se que a soma dos coeficientes no
desenvolvimento do binômio (a + b)m
é igual a 256, calcule (m/2)!
9) UFBA-88 - Calcule o termo independente de x no
desenvolvimento de (x2
+ 1/x)9
.](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-15-320.jpg)

























![41
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
Para classificar mais facilmente as proposições em falsas ou
verdadeiras, utilizam-se as chamadas tabelas-verdade.
Para negação, tem-se
p ~p
V F
F V
Atenção:
A sentença negativa é representada por “~”.
A sentença t: “O time do Paraná resistiu à pressão do São
Paulo” possui como negativa de t, ou seja “~t”, o correspondente
a: “O time do Paraná não resistiu à pressão do São Paulo”.
Observação:
Alguns matemáticos utilizam o símbolo “Ø O Brasil possui
um grande time de futebol”, que pode ser lida como “O Brasil não
possui um grande time de futebol”.
NÚMERO DE LINHAS DA TABELA VERDADE
Tabelas de Verdade
Seja “L” uma linguagem que contenha as proposições P, Q
e R.
O que podemos dizer sobre a proposição P? Para começar,
segundo o princípio de bivalência, ela é ou verdadeira ou falsa.
Isto representamos assim:
P
V
F
Agora, o que podemos dizer sobre as proposições P e Q?
Oras, ou ambas são verdadeiras, ou a primeira é verdadeira e a
segunda é falsa, ou a primeira é falsa e a segunda é verdadeira, ou
ambas são falsas. Isto representamos assim:
P Q
V V
V F
F V
F F
Como você já deve ter reparado, uma tabela para P, Q e R é
assim:
P Q R
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
Cada linha da tabela (fora a primeira que contém as fórmulas)
representa uma valoração.
Agora, o que dizer sobre fórmulas moleculares, tais como
⌐P, Q˅R, ou (Q˄R) → (P↔Q)? Para estas, podemos estabelecer
os valores que elas recebem em vista do valor de cada fórmula
atômica que as compõe. Faremos isto por meio das tabelas de
verdade.
Os primeiros passos para construir uma tabela de verdade
consistem em:
1º- Uma linha em que estão contidas todas as subfórmulas de
uma fórmula e a própria fórmula. Por exemplo, a fórmula ⌐(P˄Q)
→ R tem o seguinte conjunto de subfórmulas: [(P˄Q) → R, P˄Q,
P, Q, R]
2º) “L” linhas em que estão todos os possíveis valores que as
proposições atômicas podem receber e os valores recebidos pelas
fórmulas moleculares a partir dos valores destes átomos.
O número de linhas é L = nt
, sendo n o número de valores
que o sistema permite (sempre 2 no caso do CPC) e t o número
de átomos que a fórmula contém. Assim, se uma fórmula contém
2 átomos, o número de linhas que expressam a permutações entre
estes será 4: um caso de ambos serem verdadeiros (V V), dois casos
de apenas um dos átomos ser verdadeiro (V F , F V) e um caso no
qual ambos serem falsos (F F). Se a fórmula contiver 3 átomos, o
número de linhas que expressam a permutações entre estes será 8:
um caso de todos os átomos serem verdadeiros (V V V), três casos
de apenas dois átomos serem verdadeiros (V V F , V F V , F V V),
três casos de apenas um dos átomos ser verdadeiro (V F F , F V F ,
F F V) e um caso no qual todos átomos são falsos (F F F).
Então, para a fórmula ⌐(P˄Q) → R, temos:
P Q R P˄Q (P˄Q) → R ⌐(P˄Q) → R
V V V
V V F
V F V
V F F
F V V
F V F
F F V
F F F
Para completar esta tabela precisamos definir os operadores
lógicos. Ao fazê-lo, vamos aproveitar para explicar como
interpretá-los.
Negação
A negação tem o valor inverso da fórmula negada. A saber:
P ¬P
V F
F V
Interpretações: “Não P”, “Não é o caso de P”, “A proposição
‘P’ é falsa”.
Assim, em uma linguagem “L” na qual P significa “Sócrates é
mortal”, ¬P pode ser interpretada como «Sócrates não é mortal”,
e, se o primeiro é verdadeiro, o segundo é falso; e se o primeiro é
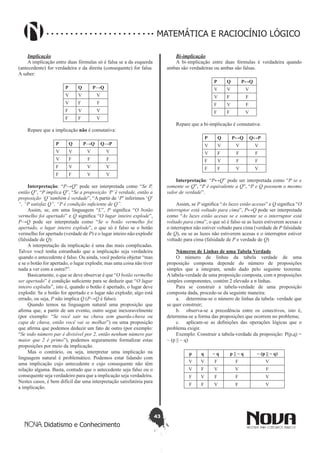
falso, o segundo é verdadeiro.](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-41-320.jpg)



































![79
Didatismo e Conhecimento
MATEMÁTICA E RACIOCÍNIO LÓGICO
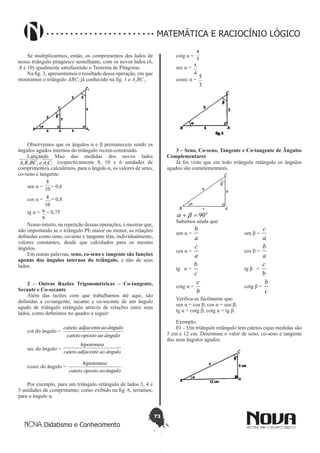
Solução:
Temos S = P(1+i)n
Logo, S/P = (1+i)n
Pelo que já conhecemos de logaritmos, poderemos
escrever:
n = log (1+ i )
(S/P) . Portanto, usando logaritmo decimal
(base 10), vem:
Temos também da expressão acima que: n.log(1 + i) =
logS – logP
Deste exemplo, dá para perceber que o estudo dos
juros compostos é uma aplicação prática do estudo dos
logaritmos.
2 – Um capital é aplicado em regime de juros compostos
a uma taxa mensal de 2% (2% a.m.). Depois de quanto tempo
este capital estará duplicado?
Solução: Sabemos que S = P (1 + i)n
. Quando o capital
inicial estiver duplicado, teremos S = 2P.
Substituindo, vem: 2P = P(1+0,02)n
[Obs: 0,02 = 2/100 =
2%]
Simplificando, fica:
2 = 1,02n
, que é uma equação exponencial simples.
Teremos então: n = log1,02
2 = log2 /log1,02 = 0,30103 /
0,00860 = 35
Nota: log2 = 0,30103 e log1,02 = 0,00860; estes valores
podem ser obtidos rapidamente em máquinas calculadoras
científicas. Caso uma questão assim caia no vestibular, o
examinador teria de informar os valores dos logaritmos
necessários, ou então permitir o uso de calculadora na prova, o
que não é comum no Brasil.
Portanto, o capital estaria duplicado após 35 meses (observe
que a taxa de juros do problema é mensal), o que equivale a 2
anos e 11 meses. Resposta: 2 anos e 11 meses.
Exercícios propostos:
1 – Um capital de $200000,00 é aplicado a juros compostos
de 10% ao ano. Calcule o montante após 4 anos.
Resposta: $292820,00
2 – Um certo capital é aplicado em regime de juros
compostos à uma taxa anual de 12%. Depois de quanto tempo
este capital estará triplicado?
Resposta: aproximadamente 9,7 anos ou aproximadamente
9 anos e 9 meses.
Observe que 9,7a = 9 + 0,7a = 9a + 0,7x12m = 9a + 8,4m
= 9a + 8m + 0,4m = 9a + 8m + 0,4x30d = 9a + 8m + 12d.
Arredondamos o resultado para maior (9 anos e 9 meses).
Nota: log3 = 0,47712 e log1,12 = 0,04922.
ANOTAÇÕES
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————
—————————————————————————](https://image.slidesharecdn.com/3-matemtica-161216004212/85/3-matematica-79-320.jpg)
