Incorporar apresentação
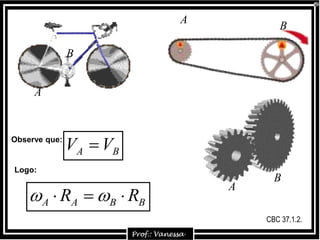
Transferir como PPSX, PPTX

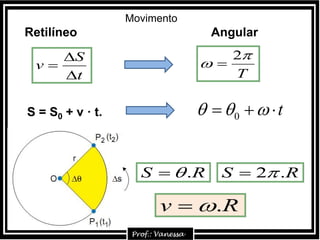

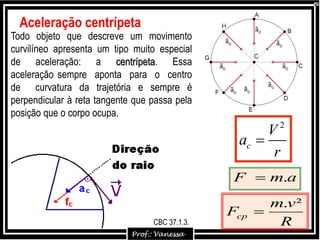
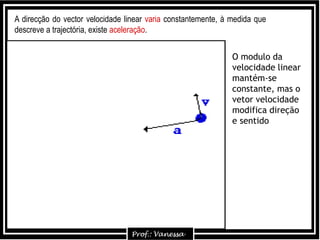

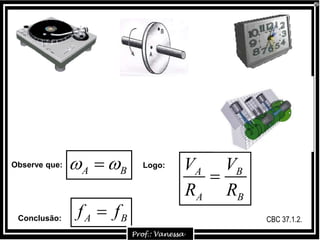
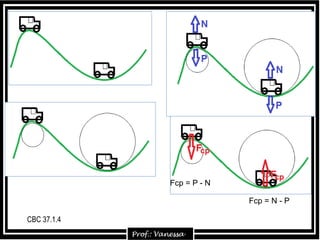
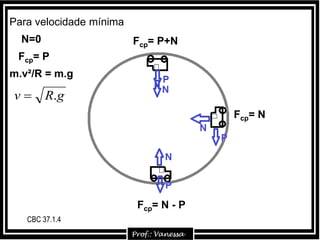
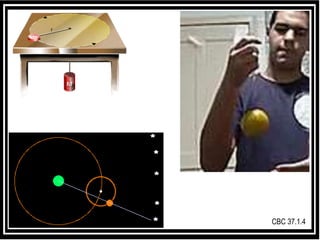

1) O documento discute conceitos sobre movimento circular uniforme (MCU), incluindo fórmulas para velocidade, período, frequência e aceleração centrípeta. 2) É explicado que a aceleração centrípeta sempre aponta para o centro da trajetória circular e é perpendicular à tangente no ponto. 3) Exemplos mostram cálculos de frequência a partir do número de revoluções e tempo, e de período a partir de frequência.











