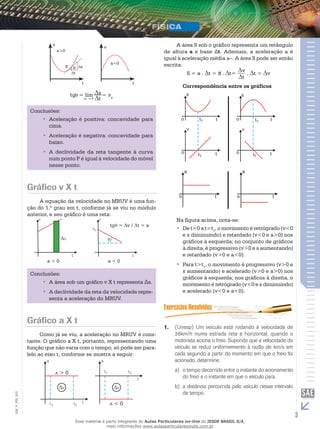
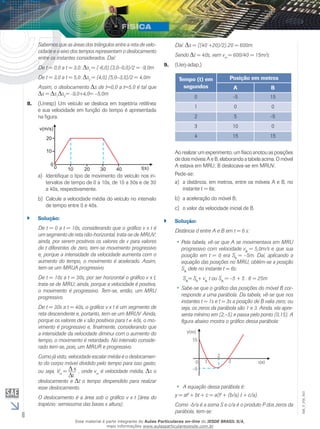
1) O documento discute os conceitos de movimento retilíneo uniformemente variado (MRUV), incluindo suas equações de velocidade, posição e aceleração.
2) Apresenta os gráficos de velocidade vs tempo, posição vs tempo e aceleração vs tempo para o MRUV.
3) Explica a correspondência entre os diferentes gráficos e como eles fornecem informações sobre o movimento.