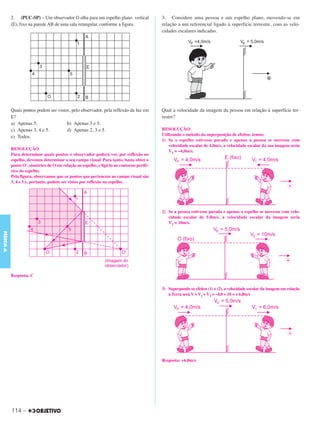
O documento apresenta um problema de física sobre movimento circular uniforme envolvendo uma bicicleta ergométrica. O problema fornece dados como o raio do disco da bicicleta e pede para:
1) Calcular a velocidade escalar de um ponto do disco quando ele completa meia volta em 1 segundo
2) Sabendo que o disco realiza 2 voltas em 30 segundos, calcular a velocidade angular média do disco nesse intervalo de tempo.