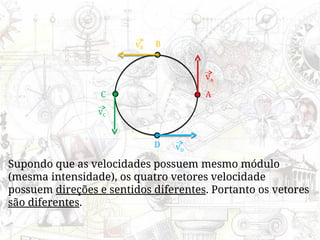
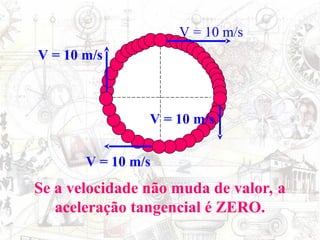
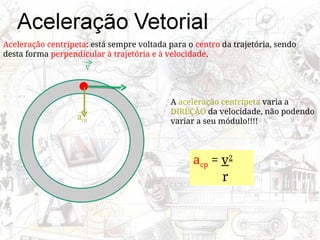
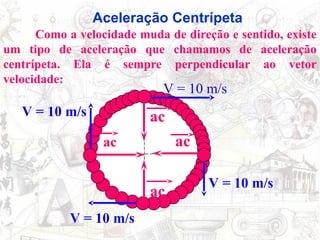
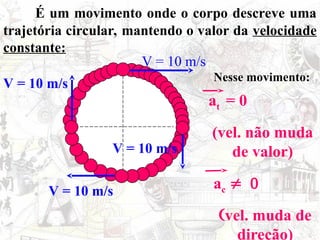
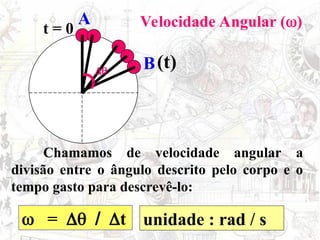
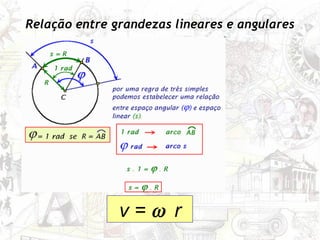
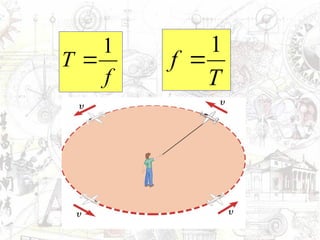
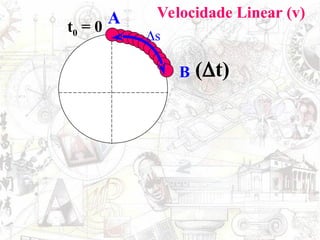
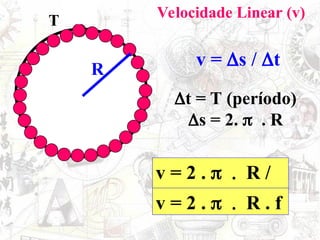
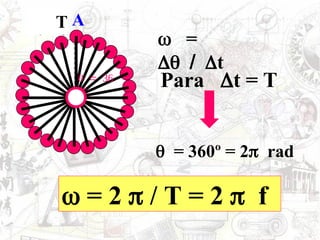
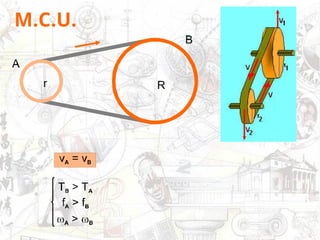
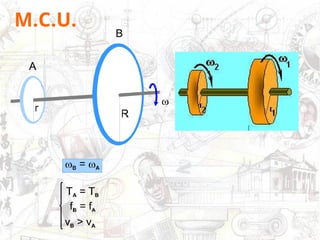
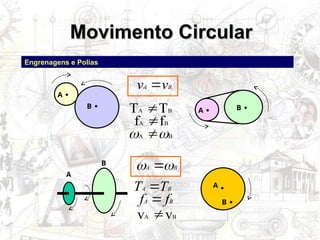
O documento aborda conceitos de movimento circular, incluindo velocidade vetorial instantânea, aceleração tangencial e centrípeta. Discute a relação entre grandezas lineares e angulares, como velocidade angular e frequência, além de apresentar fórmulas relevantes. O conteúdo se concentra na dinâmica de movimentos mantidos com velocidade constante e a interação entre acelerações e velocidades em trajetórias circulares.

1. Apostila 6A - Aula 17 e 18
Movimento Circular

2. Velocidade Vetorial Instantânea: é a velocidade do
móvel em determinado instante e sua DIREÇÃO é
TANGENTE à trajetória.
v

3. A
B
C
D
vA
vB
vC
vD
Supondo que as velocidades possuem mesmo módulo
(mesma intensidade), os quatro vetores velocidade
possuem direções e sentidos diferentes. Portanto os vetores
são diferentes.

4. Aceleração Vetorial Instantânea: é a aceleração do móvel em determinado
instante, podendo ser decomposta em duas: aceleração tangencial e
aceleração tangencial e
aceleração centrípeta.
aceleração centrípeta.
Aceleração tangencial: é tangente à trajetória e possui a mesma direção da
velocidade.
v
at
v
at
A aceleração tangencial varia o MÓDULO da velocidade, não podendo
variar a sua direção!!!!

5. Se a velocidade não muda de valor, a
aceleração tangencial é ZERO.
V = 10 m/s
V = 10 m/s
V = 10 m/s
V = 10 m/s

6. Aceleração centrípeta: está sempre voltada para o centro da trajetória, sendo
desta forma perpendicular à trajetória e à velocidade.
v
acp
A aceleração centrípeta varia a
DIREÇÃO da velocidade, não podendo
variar a seu módulo!!!!
acp = v2
r

7. Como a velocidade muda de direção e sentido, existe
um tipo de aceleração que chamamos de aceleração
centrípeta. Ela é sempre perpendicular ao vetor
velocidade:
V = 10 m/s
ac
V = 10 m/s
ac
V = 10 m/s
ac
V = 10 m/s
ac
Aceleração Centrípeta

8. A aceleração vetorial é a soma vetorial da aceleração tangencial com a
aceleração centrípeta.
a = at + acp
at
acp
a
Para o cálculo do módulo, utilizamos Pitágoras.
a2
= at
2
+
acp
2

10. É um movimento onde o corpo descreve uma
trajetória circular, mantendo o valor da velocidade
constante:
Nesse movimento:
at = 0
(vel. não muda
de valor)
ac 
vel. muda de
direção)
V = 10 m/s
V = 10 m/s
V = 10 m/s
V = 10 m/s

12. Chamamos de velocidade angular a
divisão entre o ângulo descrito pelo corpo e o
tempo gasto para descrevê-lo:
 = t unidade : rad / s
A
t = 0
B(t)

Velocidade Angular ()


13. A velocidade angular de cada
homem abaixo é igual ou
diferente? E a velocidade
escalar?

14. Relação entre grandezas lineares e angulares
v = r

15. r
r
r
r
v
a 2
2
2
c
)
(






16. t = 0
T
O PERÍODO DO MCU É O TEMPO GASTO
PARA DAR UMA VOLTA COMPLETA. SUA
UNIDADE (NO SI) É O SEGUNDO (s).
PERÍODO (T)

17. t = 0
1s
A FREQUÊNCIA É O Nº DE VOLTAS DADAS
DADAS POR UNIDADE DE TEMPO. A FREQUÊNCIA
É O INVERSO DO PERÍODO. SUA UNIDADE (NO SI)
É O HERTZ (Hz = 1/s).
FREQUÊNCIA (f)
f

18. f
T
1

T
f
1


19. A
t0 = 0
B (t)
s
Velocidade Linear (v)

20. v = s / t
t = T (período)
s = 2. . R
v = 2 . R /
T
t = 0
T
R
Velocidade Linear (v)
v = 2 . R . f

21.  =
t
A
t = 0
T

º
Para t = T
= 360º = 2 rad
 = 2  / T = 2 f

22. Velocidade angular: 
f i
  
  
Velocidade angular 
Δt
Δθ
ω 
A unidade SI da velocidade angular  é radianos por segundo rad s-1
.
O ângulo ao centro  vem expresso em radianos (rad).
A velocidade angular tem valores constantes porque são descritos
ângulos ao centro, de igual amplitude, em intervalos de tempo iguais.

24. M.C.U.

25. M.C.U.

26. Movimento Circular
Movimento Circular
Engrenagens e Polias
B
A v
v 
B
A T
T 
B
A 
 
A
B
B
A 
 
A B
B
A T
T 
B
A v
v 
B
A f
f 
B
A f
f 
B
A
A
B