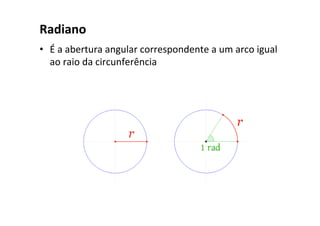
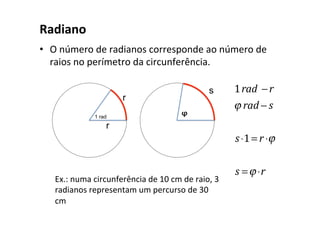
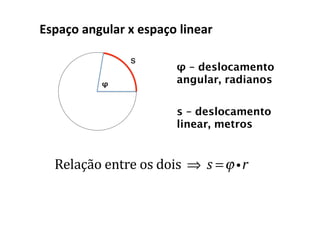
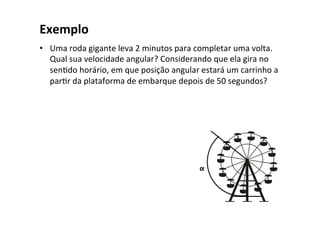
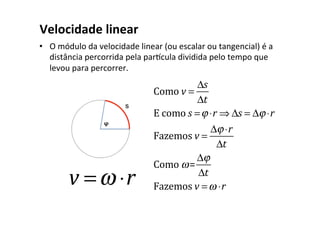
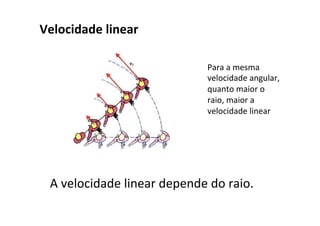
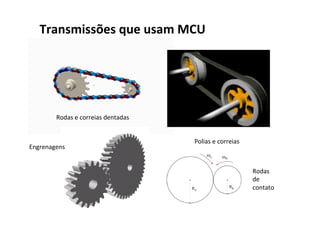
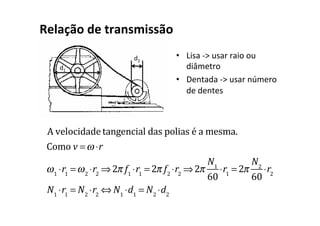
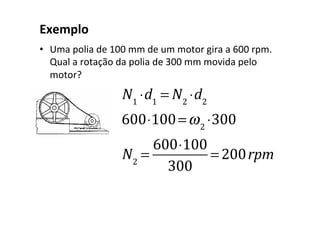
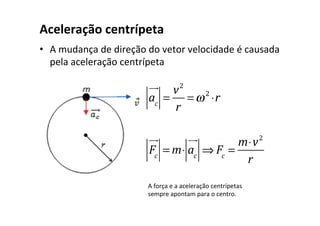
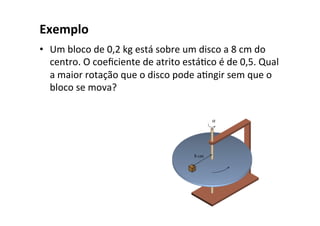
O documento discute conceitos fundamentais do movimento circular uniforme, incluindo radianos, relação entre graus e radianos, período e frequência, velocidade angular, posição angular, velocidade linear, aceleração centrípeta e força centrípeta. Exemplos ilustram como calcular estas grandezas para objetos em movimento circular.