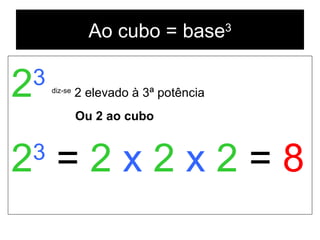
Este documento explica o conceito de potências e expoentes. Resume que potências representam a multiplicação de um número por si mesmo várias vezes e são escritas na forma de uma base e um expoente. O expoente indica quantas vezes a base é multiplicada. O documento fornece exemplos de como ler e escrever potências e discute erros comuns.

1. Potências e Expoentes Retirado e traduzido do SlideShare do Username taleese This is a portuguese translation of “Powers and Exponents”, user taleese.

2. Multiplicação = adição de parcelas iguais Quando precisamos adicionar um número consigo próprio várias vezes, a multiplicação é utilizada porque se trata de uma adição com parcelas iguais . Em vez de adicionar 2 + 2 + 2 + 2 + 2 = 10 Multiplica-se 2 x 5 (e obtém-se a mesma resposta) = 10

3. Potências = multiplicação de factores iguais Quando precisamos multiplicar o mesmo número por si próprio várias vezes, as potências são a multiplicação de factores iguais . Em vez de multiplicar 2 x 2 x 2 x 2 x 2 = 32 Usa-se a potência 2 5 (e obtém-se o mesmo resultado) = 32

4. potência = um número escrito assim: uma base e um expoente. base expoente Assim: 2 5 diz-se 2 elevado à 5ª potência

5. A base (número maior em baixo) = o factor que se repete na multiplicação. base expoente = potência factor x factor x factor x factor x factor = produto 2 x 2 x 2 x 2 x 2 = 32

6. O expoente (número pequeno à direita e acima da base) = o número de vezes que a base é multiplicada por si própria. 2 5 2 (1ª vez) x 2 (2ª vez) x 2 (3ª vez) x 2 (4ª vez) x 2 (5ª vez) = 32

7. Como ler potências e expoentes Normalmente, diz-se “ o número base elevado a número expoente (expresso como número ordinal) potência” 2 5 diz-se 2 elevado à 5ª potência Números ordinais: 1 a , 2 a , 3 a , 4 a , 5 a ,…

8. Ao quadrado = base 2 2 2 diz-se 2 elevado à 2ª potência Ou 2 ao quadrado 2 2 = 2 x 2 = 4

9. Ao cubo = base 3 2 3 diz-se 2 elevado à 3ª potência Ou 2 ao cubo 2 3 = 2 x 2 x 2 = 8

10. Erros mais comuns 2 5 ≠ (não é igual a) 2 x 5 2 5 ≠ (não é igual a) 10 2 5 = 2 x 2 x 2 x 2 x 2 = 32

11. Quando o expoente é 1 , A resposta é o número que está na base . 2 1 = 2 4638 1 = 4638 qualquer número 1 = o mesmo da base

12. O expoente 1 normalmente não se escreve .

13. “ Escrever uma potência como um produto …” potência = forma curta de escrever Isto é 2 5 = 2 x 2 x 2 x 2 x 2 produto = forma longa de escrever a resposta

14. “ Encontrar o valor da potência …” Quer dizer resposta 2 5 = 2 x 2 x 2 x 2 x 2 = 32 potência = produto dos factores = (e ao valor da potência)

15. “ Escrever factores primos usando expoentes…” 125 = produto 5 x 5 x 5 ou 125 = potência 5 3 = resposta usando expoentes produto 5 x 5 x 5 = potência 5 3 A mesma resposta escrita de duas maneiras diferentes.

16. Congratulations! Now you know how to write a multiplication problem as a product using factors, or as a power using exponents (this can be called exponential form ). You know how to (evaluate) find the value (answer) of a power.

17. Notes for teachers Correlates with Glencoe Mathematics (Florida Edition) texts: Mathematics: Applications and Concepts Course 1: (red book) Chapter 1 Lesson 4 Powers and Exponents Mathematics: Applications and Concepts Course 2: (blue book) Chapter 1 Lesson 2: Powers and Exponents Pre-Algebra: (green book) Chapter 4 Lesson 2: Powers and Exponents For more information on my math class see http:// walsh.edublogs.org