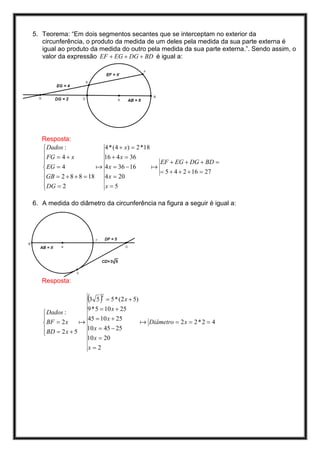
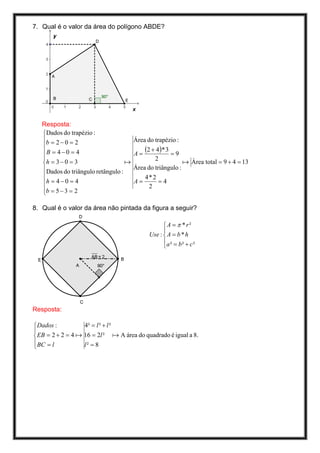
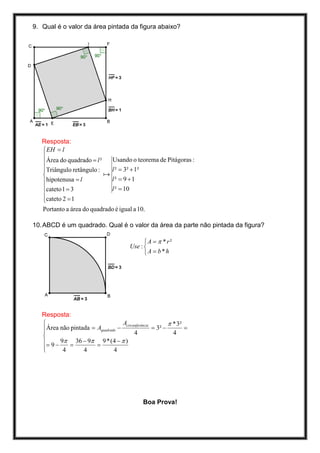
O documento apresenta 10 questões sobre geometria envolvendo cálculos com figuras geométricas como triângulos, circunferências e polígonos. As respostas fornecem os cálculos detalhados para encontrar valores como raios, áreas e medidas de segmentos utilizando fórmulas geométricas como o Teorema de Pitágoras.

1. ALUNO(A) Nº
Gabarito.
SÉRIE ENSINO TURNO NOTA
9º ano Fundamental II Manhã
PROFESSOR(A) DATA
Joelson Lima
Verificação final da 2ª etapa pedagógica
Observação: é obrigatório apresentar todos os cálculos de maneira organizada usando lápis
(grafite).
1. Sabendo que um triângulo inscrito numa circunferência cujo lado coincide com o
diâmetro, é chamado triangulo retângulo, qual é o valor do raio da circunferência da
figura abaixo?
a = n + m = 2 * r
a ² = b ² + c ²


USE : b ² = a * m
c ² = a * n

h ² = m * n

Resposta:
 Dados : h² = m * n a = m + n = 2r
h = 8 8² = 4 x 4 + 16 = 2r

 → →
m = 4 64 = 4 x 2r = 10
n = x
 x = 16 r = 10
Portanto o raio é igual a 10
2. Observando a figura a seguir, qual é o valor de x ² ?
Resposta:
Pelo teorema de Pitágoras :
 Dados : a ² = b² + c²
 AB = 5 8² = x ² + 5²

 →
 AD = 3 + 5 = 8 64 = x ² + 25
 AC = 5
 x ² = 64 − 25
x ² = 39

2. 3. O teorema das cordas diz: “Se duas cordas de uma circunferência se interceptam, o
produto das medidas dos segmentos determinados sobre uma delas é igual ao produto
das medidas dos segmentos determinados sobre a outra.”. Na figura a seguir, o valor
das medidas dos segmentos DF e CF, valem respectivamente:
Resposta:
x * 9 = 6 * ( x + 1)
9x = 6x + 6
DF = 2
9x − 6x = 6 →
CF = 2 + 1 = 3
3x = 6
x=2
4. O valor de x na figura a seguir é igual a:
Resposta:
 Dados :
 AG = AB = 13 x * x = 8 * 18

 x ² = 144
CG = 8 a
 AC = AG − CG = 13 − 8 = 5 x = 144
 x = 12
CB = 13 + 5 = 18


3. 5. Teorema: “Em dois segmentos secantes que se interceptam no exterior da
circunferência, o produto da medida de um deles pela medida da sua parte externa é
igual ao produto da medida do outro pela medida da sua parte externa.”. Sendo assim, o
valor da expressão EF + EG + DG + BD é igual a:
Resposta:
 Dados : 4 * (4 + x) = 2 *18
 FG = 4 + x 16 + 4 x = 36

 EF + EG + DG + BD =
 EG = 4 a 4 x = 36 − 16 a
GB = 2 + 8 + 8 = 18 = 5 + 4 + 2 + 16 = 27
4 x = 20


 DG = 2 x=5
6. A medida do diâmetro da circunferência na figura a seguir é igual a:
Resposta:
(3 5 )2
= 5 * (2 x + 5)
9 * 5 = 10 x + 25
 Dados :
 45 = 10 x + 25
 BF = 2 x a a Diâmetro = 2 x = 2 * 2 = 4
 BD = 2 x + 5 10 x = 45 − 25

10 x = 20
x=2

4. 7. Qual é o valor da área do polígono ABDE?
Resposta:
Dados do trapézio :
b = 2 − 0 = 2 Área do trapézio :

B = 4 − 0 = 4 A=
(2 + 4)* 3 = 9
 2
h = 3 − 0 = 3 a a Área total = 9 + 4 = 13
Dados do triângulo retângulo : Área do triângulo :
 4* 2
h = 4 − 0 = 4 A= =4
b = 5 − 3 = 2 2

8. Qual é o valor da área não pintada da figura a seguir?
A = π * r²

Use :  A = b * h
a ² = b ² + c ²

Resposta:
 Dados : 4² = l ² + l ²

 EB = 2 + 2 = 4 a 16 = 2l ² a A área do quadrado é igual a 8.
 BC = l l² = 8


5. 9. Qual é o valor da área pintada da figura abaixo?
Resposta:
 EH = l

Área do quadrado = l ² Usando o teorema de Pitágoras :
Triângulo retângulo :
 l ² = 3² + 1²
 a
 hipotenusa = l l² = 9 +1
cateto 1 = 3 l ² = 10

cateto 2 = 1

Portanto a área do quadrado é igual a 10.
10. ABCD é um quadrado. Qual é o valor da área da parte não pintada da figura?
A = π *r²
Use : 
A = b*h
Resposta:
 Acircunferência π * 3²
Área não pintada = Aquadrado −
 4
= 3² −
4
=

= 9 − 9π = 36 − 9π = 9 * (4 − π )

 4 4 4
Boa Prova!