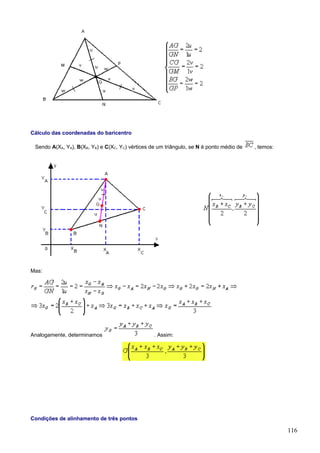
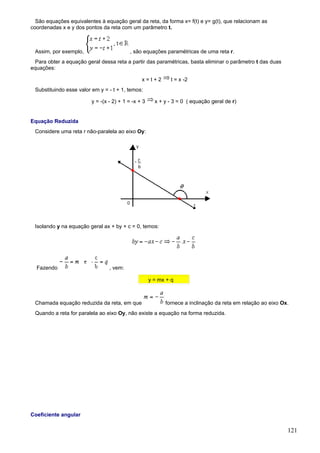
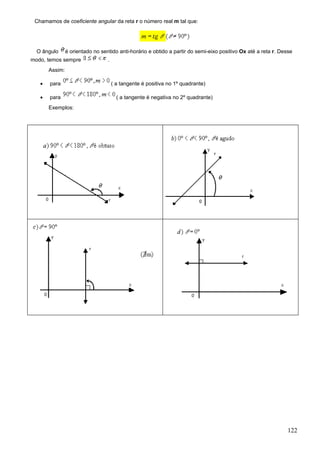
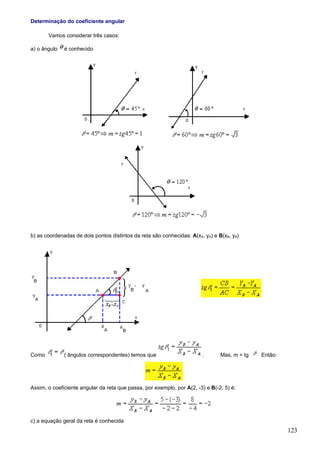
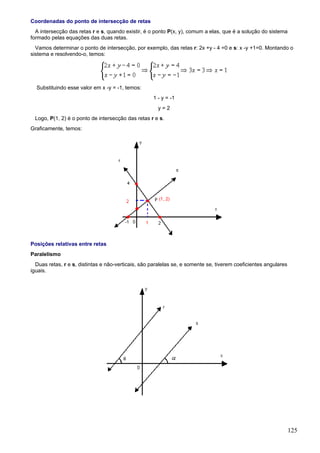
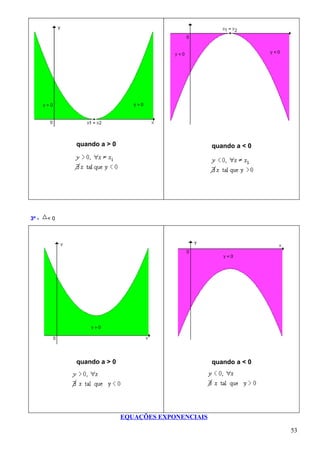
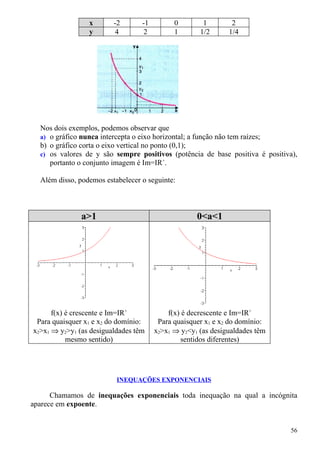
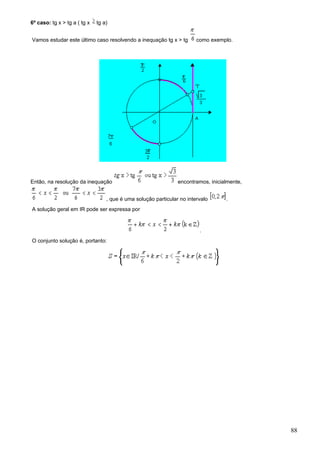
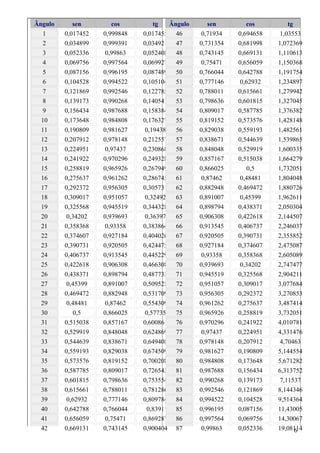
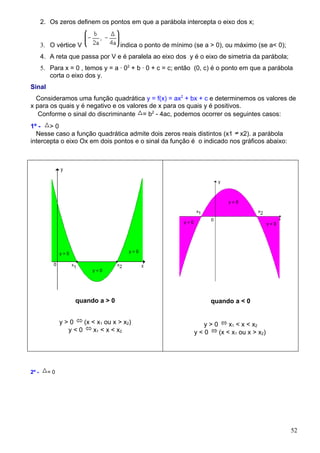
1. O documento apresenta fórmulas e definições de conceitos fundamentais de combinatória e probabilidade como fatorial, arranjo simples, permutação simples e combinação simples. 2. São resolvidos exercícios envolvendo cálculos com essas fórmulas e conceitos, como calcular expressões com fatoriais, determinar possibilidades de arranjos e permutações. 3. A tabela trigonométrica fornece valores de seno, cosseno e tangente para ângulos de 1 a 90 graus.

1. Análise Combinatória
Fatorial de um número:
n!=n.(n-1).(n-2)...3.2.1
Definições especiais:
0!=1
1!=1
100!+101!
1) Calcule o valor da expressão .
99!
100!+101! 100.99!+101.100.99!
= = 100 + 101.100 = 100 + 10100 = 10200
99! 99!
( x + 1)!
2) Resolva a equação = 56.
( x − 1)!
( x + 1)! ( x + 1)( x)( x − 1)!
= 56 ⇒ = 56 ⇒ ( x + 1)( x) = 56 ⇒ x 2 + x = 56 ⇒
( x − 1)! ( x − 1)!
− 1 ± 225 − 1 ± 15 x = 7
⇒ x 2 + x − 56 = 0 ⇒ x = ⇒ x= ⇒
2 2 x = -8
Resposta : x = 7, pois não existe fatorial de um número negativo.
3) Quatro times de futebol (Grêmio, Santos, São Paulo e Flamengo) disputam o torneio dos
campeões do mundo. Quantas são as possibilidades para os três primeiros lugares?
R : Existem 4 possibilidades para o 1º lugar, sobrando 3 possibilidades para o 2º lugar e 2
possibilidades para o 3º lugar → 4.3.2 = 24 possibilidades.
Arranjo simples:
n!
An , p =
(n − p)!
A6, 2 + A4,3 − A5, 2
4) Calcule .
A9, 2 + A8,1
6! 4! 5!
+ −
A6, 2 + A4,3 − A5, 2 (6 − 2)! (4 − 3)! (5 − 2)! 30 + 24 − 20 34 17
= = = =
A9, 2 + A8,1 9! 8! 72 + 8 80 40
+
(9 − 2)! (8 − 1)!
1

2. 5) Quantos números de 3 algarismos distintos podemos formar com o algarismos do
sistema decimal (0,1,2,3,4,5,6,7,8,9) sem os repetir, de modo que :
a) COMECEM COM 1.
R : O número pode possuir três algarismos, sendo que para o primeiro existe apenas 1
possibilidade (1) e para os outros dois ainda existem 9 números disponíveis :
9! 9! 9.8.7!
1. A9, 2 = = = = 9.8 = 72 números.
(9 − 2)! 7! 7!
b) COMECEM COM 2 E TERMINEM COM 5.
R : Para o primeiro algarismo existe apenas 1 possibilidade (2), e para o terceiro também
existe apenas 1 possibilidade (5). Para o segundo ainda existem 8 possibilidades :
8! 8! 8.7!
1.1. A8,1 = = = = 8 números.
(8 − 1)! 7! 7!
c) SEJAM DIVISÍVEIS POR 5.
R : Para um número ser divisível 5, ele deve terminar com 0 ou com 5. Primeiramente
vamos calcular o número de divisíveis por 5 que terminam com 0 :
→ Para o terceiro algarismo existe apenas 1 possibilidade (0), e para os dois primeiros ainda
existem 9 números disponíveis. Portanto o número de divisíveis por 5 que terminam com 0 é :
9! 9! 9.8.7!
1. A9, 2 = = = = 9.8 = 72 números.
(9 − 2)! 7! 7!
→ Agora calculamos quantos divisíveis por 5 terminam com 5 : para o terceiro algarismo
existe apenas uma possibilidade (5). Para o primeiro algarismo existem ainda 8 possibilidades,
pois o número não pode começar com 0 (senão seria um número de 2 algarismos). E para o
segundo algarismo também existem 8 possibilidades (o segundo algarismo pode ser 0).
8! 8! 8! 8! 8.7! 8.7!
1. A8,1 . A8,1 = . = . = . = 8.8 = 64 números.
(8 − 1)! (8 − 1)! 7! 7! 7! 7!
Resposta : O número de divisíveis por 5 é 72 + 64 = 136 números.
6) Quantos são os números compreendidos entre 2000 e 3000 formados por algarismos
distintos escolhidos entre 1,2,3,4,5,6,7,8 e 9?
R : O número deve ter quatro algarismos (pois está entre 2000 e 3000). Para o primeiro
algarismo existe apenas uma possibilidade (2), e para os outros três ainda existem 8 números
disponíveis, então :
8! 8! 8.7.6.5!
1. A8,3 = = = = 8.7.6 = 336 números.
(8 − 3)! 5! 5!
2

3. Permutação Simples: É um caso particular de arranjo simples. É o tipo de agrupamento ordenado onde
entram todos os elementos.
Pn = n!
7) Quantos números de 5 algarismos distintos podem ser formados por 1,2,3,5 e 8?
P5 = 5! = 5.4.3.2.1 = 120 números.
8) Quantos anagramas da palavra EDITORA :
a) COMEÇAM POR A.
Para a primeira letra existe apenas uma possibilidade (A), e para as outras 6 letras
existem 6 possibilidades. Então o total é :
1.P6 = 1.6!= 6.5.4.3.2.1 = 720 anagramas.
b) COMEÇAM POR A e terminam com E.
Para a primeira letra existe 1 possibilidade (A), e para última também só existe 1 (E),
e para as outras 5 letras existem 5 possibilidades. Então o total é :
1.1.P5 = 1.1.5!= 5.4.3.2.1 = 120 anagramas.
8) Calcule de quantas maneiras podem ser dipostas 4 damas e 4 cavalheiros, numa fila, de
forma que não fiquem juntos dois cavalheiros e duas damas.
R :Existem duas maneiras de fazer isso :
C - D - C - D - C - D - C - D ou D - C - D - C - D - C - D - C
Colocando um cavalheiro na primeira posição temos como número total de maneiras :
P4 .P4 = 4!.4!= 24.24 = 576 maneiras.
Colocando uma dama na primeira posição temos também :
P4 .P4 = 4!.4!= 24.24 = 576 maneiras.
Portanto o total é 576 + 576 = 1152 maneiras.
Combinação Simples: é o tipo de agrupamento em que um grupo difere do outro apenas pela natureza
dos elementos componentes.
n!
Cn, p =
p!(n − p )!
3

4. 9) Resolver a equação C m,3 − C m , 2 = 0.
m! m!
− =0
3!(m − 3)! 2!(m − 2)!
m.(m − 1).(m − 2).(m − 3)! m.(m − 1).(m − 2)!
− =0
3!( m − 3)! 2!(m − 2)!
m.(m − 1).(m − 2) m.(m − 1)
− =0
3! 2!
m 3 − 2m 2 − m 2 + 2m m 2 − m
− =0
6 2
m 3 − 3m 2 + 2m − 3m 2 + 3m
= 0 ⇒ m 3 − 6m 2 + 5m = 0
6
6 ± 16 m ' = 5
m 2 − 6m + 5 = 0 ⇒ m = ⇒ 
2 m ' ' = 1
Resposta : m = 5.
obs : m = 1 não é a resposta porque não pode haver C1,3 .
10) Com 10 espécies de frutas, quantos tipos de salada, contendo 6 espécies diferentes
podem ser feitas?
10! 10.9.8.7.6! 5040 5040
C10,6 = = = = = 210 tipos de saladas.
6!.(10 − 6)! 6!.4! 4! 24
11) Numa reunião com 7 rapazes e 6 moças, quantas comissões podemos formar com 3
rapazes e 4 moças?
RAPAZES - C 7 ,3
MOÇAS - C 6, 4
O resultado é o produto C 7 ,3 .C 6, 4 .
7! 6! 7.6.5.4! 6.5.4! 210 30
. = . = . = 35.15 = 525 comissões.
3!(7 − 3)! 4!(6 − 4)! 3!.4! 4!.2! 3! 2
TEORIA DOS CONJUNTOS
4

5. Símbolos
: pertence : existe
: não pertence : não existe
: está contido : para todo (ou qualquer que seja)
: não está contido : conjunto vazio
: contém N: conjunto dos números naturais
: não contém Z : conjunto dos números inteiros
/ : tal que Q: conjunto dos números racionais
: implica que Q'= I: conjunto dos números irracionais
: se, e somente se R: conjunto dos números reais
Veja também: Símbolos das operações - Conceitos sobre conjuntos
TABELA TRIGONOMÉTRICA
5

6. Ângulo sen cos tg Ângulo sen cos tg
1 0,017452 0,999848 0,017455 46 0,71934 0,694658 1,03553
2 0,034899 0,999391 0,034921 47 0,731354 0,681998 1,072369
3 0,052336 0,99863 0,052408 48 0,743145 0,669131 1,110613
4 0,069756 0,997564 0,069927 49 0,75471 0,656059 1,150368
5 0,087156 0,996195 0,087489 50 0,766044 0,642788 1,191754
6 0,104528 0,994522 0,105104 51 0,777146 0,62932 1,234897
7 0,121869 0,992546 0,122785 52 0,788011 0,615661 1,279942
8 0,139173 0,990268 0,140541 53 0,798636 0,601815 1,327045
9 0,156434 0,987688 0,158384 54 0,809017 0,587785 1,376382
10 0,173648 0,984808 0,176327 55 0,819152 0,573576 1,428148
11 0,190809 0,981627 0,19438 56 0,829038 0,559193 1,482561
12 0,207912 0,978148 0,212557 57 0,838671 0,544639 1,539865
13 0,224951 0,97437 0,230868 58 0,848048 0,529919 1,600335
14 0,241922 0,970296 0,249328 59 0,857167 0,515038 1,664279
15 0,258819 0,965926 0,267949 60 0,866025 0,5 1,732051
16 0,275637 0,961262 0,286745 61 0,87462 0,48481 1,804048
17 0,292372 0,956305 0,305731 62 0,882948 0,469472 1,880726
18 0,309017 0,951057 0,32492 63 0,891007 0,45399 1,962611
19 0,325568 0,945519 0,344328 64 0,898794 0,438371 2,050304
20 0,34202 0,939693 0,36397 65 0,906308 0,422618 2,144507
21 0,358368 0,93358 0,383864 66 0,913545 0,406737 2,246037
22 0,374607 0,927184 0,404026 67 0,920505 0,390731 2,355852
23 0,390731 0,920505 0,424475 68 0,927184 0,374607 2,475087
24 0,406737 0,913545 0,445229 69 0,93358 0,358368 2,605089
25 0,422618 0,906308 0,466308 70 0,939693 0,34202 2,747477
26 0,438371 0,898794 0,487733 71 0,945519 0,325568 2,904211
27 0,45399 0,891007 0,509525 72 0,951057 0,309017 3,077684
28 0,469472 0,882948 0,531709 73 0,956305 0,292372 3,270853
29 0,48481 0,87462 0,554309 74 0,961262 0,275637 3,487414
30 0,5 0,866025 0,57735 75 0,965926 0,258819 3,732051
31 0,515038 0,857167 0,600861 76 0,970296 0,241922 4,010781
32 0,529919 0,848048 0,624869 77 0,97437 0,224951 4,331476
33 0,544639 0,838671 0,649408 78 0,978148 0,207912 4,70463
34 0,559193 0,829038 0,674509 79 0,981627 0,190809 5,144554
35 0,573576 0,819152 0,700208 80 0,984808 0,173648 5,671282
36 0,587785 0,809017 0,726543 81 0,987688 0,156434 6,313752
37 0,601815 0,798636 0,753554 82 0,990268 0,139173 7,11537
38 0,615661 0,788011 0,781286 83 0,992546 0,121869 8,144346
39 0,62932 0,777146 0,809784 84 0,994522 0,104528 9,514364
40 0,642788 0,766044 0,8391 85 0,996195 0,087156 11,43005
41 0,656059 0,75471 0,869287 86 0,997564 0,069756 14,30067
42 0,669131 0,743145 0,900404 87 0,99863 0,052336 19,08114
6

7. Vetores
Reta Orientada - Eixo
Uma reta r é orientada quando fixa nela um sentido de percurso, considerado positivo e indicado por uma
seta.
Segmento orientado
Um segmento orientado é determinado por um par ordenado de pontos, o primeiro chamado origem do
segmento, o segundo chamado extremidade.
Segmento Nulo
Um segmento nulo é aquele cuja extremidade coincide com a origem.
Segmentos Opostos
Se AB é um segmento orientado, o segmento orientado BA é oposto de AB.
Medida de um Segmento
Fixada uma unidade de comprimento, cada segmento orientado pode-se associar um número real, não
negativo, que é a medida do segmento em relação aquela unidade. A medida do segmento orientado é o seu
comprimento ou seu módulo. O comprimento do segmento AB é indicado por .
Assim, o comprimento do segmento AB representado na figura abaixo é de 5 unidades de comprimento:
= 5 u.c.
Observações
a. Os segmentos nulos têm comprimento igual a zero
b. = .
Vetores
Direção e Sentido
Dois segmentos orientados não nulos AB e CD têm a mesma direção se as retas suportes desses
segmentos são paralelas:
7

8. ou coincidentes
Observações
a. Só se pode comparar os sentidos de dois segmentos orientados se eles têm mesma direção.
b. Dois Segmentos orientados opostos têm sentidos contrários.
Segmentos Equipolentes
Dois segmentos orientados AB e CD são equipolentes quando têm a mesma direção, o mesmo sentido e o
mesmo comprimento.
Se os segmentos orientados AB e CD não pertencem à mesma reta. Na segunda figura abaixo, para que AB
seja equipolente a CD é necessário que AB//CD e AC/BD, isto é, ABCD deve ser um paralelogramo.
Observações
a. Dois segmentos nulos são sempre equipolentes.
b. A equipolência dos segmentos AB e CD é representada por AB ~ CD.
8

9. Propriedades da Equipolência
I. AB ~ AB (reflexiva).
II. Se AB ~ CD, CD ~ AB (simétrica).
III. Se AB ~ CD e CD ~ EF, AB ~ EF (transitiva).
IV. Dado o segmento orientado AB e um ponto C, existe um único ponto D tal que AB ~ CD.
Vetor
Vetor determinado por um segmento orientado AB é o conjunto de todos os segmentos orientados
equipolentes a AB.
Se indicarmos com este conjunto, simbolicamente poderemos escrever:
= {XY/XY ~ AB}
onde XY é um segmento qualquer do conjunto.
O vetor determinado por AB é indicado por ou B - A ou .
um mesmo vetor é determinado por uma infinidade de segmentos orientados, chamados representantes
desse vetor, e todos equipolentes entre si. Assim, um segmento determina um conjunto que é o vetor, e
qualquer um destes representantes determina o mesmo vetor. Usando um pouco mais nossa capacidade de
abstração, se considerarmos todos os infinitos segmentos orientados de origem comum, estaremos
caracterizando, através de representantes, a totalidade dos vetores do espaço. Ora, cada um destes
segmentos é um representante de um só vetor. Conseqüentemente, todos os vetores se acham representados
naquele conjunto que imaginamos.
As características de um vetor são as mesmas de qualquer um de seus representantes, isto é: o módulo,
a direção e o sentido do vetor são o módulo, direção e o sentido de qualquer um de seus representantes.
O módulo de se indica por | | .
Vetores iguais
Dois vetores e são iguais se, e somente se, AB ~ CD.
Vetor Nulo
Os segmentos nulos, por serem equipolentes entre si, determinam um único vetor, chamado vetor nulo ou
vetor zero, e que é indicado por .
Vetores Opostos
Dado um vetor = , o vetor é o oposto de e se indica por ou por .
9

10. Vetor Unitário
Um vetor é unitário se | | = 1.
Versor
Versor de um vetor não nulo é o vetor unitário de mesma direção e mesmo sentido de .
Por exemplo, tomemos um vetor de módulo 3.
Os vetores e da figura são vetores unitários, pois ambos têm módulo 1. No entanto, apenas tem a
mesma direção e o mesmo sentido de . Portanto, este é o versor de .
Vetores Colineares
Dois vetores e são colineares se tiverem a mesma direção. Em outras palavras: e são colineares se
tiverem representantes AB e CD pertencentes a uma mesma reta ou a retas paralelas.
Vetores Coplanares
10

11. Se os vetores não nulos , e (não importa o número de vetores) possuem representantes AB, CD e EF
pertencentes a um mesmo plano π, diz-se que eles são coplanares.
Dois vetores e quaisquer são são sempre coplanares, pois podemos sempre tomar um ponto no
espaço e, com origem nele, imaginar os dois representantes de e pertencendo a um plano p que passa por
este ponto.
Três vetores poderão ou não ser coplanares.
, e são coplanares
, e não são coplanares
Soma de vetores
Se v=(a,b) e w=(c,d), definimos a soma de v e w, por:
v + w = (a+c,b+d)
Propriedades da soma de vetores
I) Comutativa: Para todos os vetores u e v de R2:
11

12. v+w=w+v
II) Associativa: Para todos os vetores u, v e w de R2:
u + (v + w) = (u + v) + w
III) Elemento neutro: Existe um vetor O=(0,0) em R2 tal que para todo vetor u de R2, se tem:
O+u=u
IV) Elemento oposto: Para cada vetor v de R2, existe um vetor -v em R2 tal que:
v + (-v) = O
Diferença de vetores
Se v=(a,b) e w=(c,d), definimos a diferença entre v e w, por:
v - w = (a-c,b-d)
Produto de um escalar por um vetor
Se v=(a,b) é um vetor e c é um número real, definimos a multiplicação de c por v, como:
c.v = (ca,cb)
Propriedades do produto de escalar por vetor
Quaisquer que sejam k e c escalares, v e w vetores:
• 1v=v
• (k c) v = k (c v) = c (k v)
• k v = c v implica k = c, se v for não nulo
• k (v+w) = k v + k w
• (k + c)v = k v + c v
Módulo de um vetor
O módulo ou comprimento do vetor v=(a,b) é um número real não negativo, definido por:
Vetor unitário
Vetor unitário é o que tem o módulo igual a 1.
Existem dois vetores unitários que formam a base canônica para o espaço R2, que são dados por:
i = (1,0) j = (0,1)
Para construir um vetor unitário u que tenha a mesma direção e sentido que um outro vetor v, basta dividir o vetor v pelo
seu módulo, isto é:
Observação:
12

13. Para construir um vetor u paralelo a um vetor v, basta tomar u=cv onde c é um escalar não nulo. Nesse caso, u e v serão
paralelos.
Se c = 0 então u será o vetor nulo.
Se 0 < c < 1 então u terá comprimento menor do que v.
Se c > 1 então u terá comprimento maior do que v.
Se c < 0 então u terá sentido oposto ao de v.
Próximo tópico:
Produto escalar, Propriedades do produto escalar, Ângulos entre dois vetores, Vetores ortogonais
PROBABILIDADE
A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o
motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da
probabilidade permite que se calcule a chance de ocorrência de um número em um experimento aleatório.
Experimento Aleatório
13

14. É aquele experimento que quando repetido em iguais condições, podem fornecer resultados diferentes, ou
seja, são resultados explicados ao acaso. Quando se fala de tempo e possibilidades de ganho na loteria, a
abordagem envolve cálculo de experimento aleatório.
Espaço Amostral
É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o espaço
amostral, é S.
Exemplo:
Lançando uma moeda e um dado, simultaneamente, sendo S o espaço amostral, constituído pelos 12
elementos:
S = {K1, K2, K3, K4, K5, K6, R1, R2, R3, R4, R5, R6}
1. Escreva explicitamente os seguintes eventos: A={caras e m número par aparece}, B={um número
primo aparece}, C={coroas e um número ímpar aparecem}.
2. Idem, o evento em que:
a) A ou B ocorrem;
b) B e C ocorrem;
c) Somente B ocorre.
3. Quais dos eventos A,B e C são mutuamente exclusivos
Resolução:
1. Para obter A, escolhemos os elementos de S constituídos de um K e um número par: A={K2, K4, K6};
Para obter B, escolhemos os pontos de S constituídos de números primos: B={K2,K3,K5,R2,R3,R5}
Para obter C, escolhemos os pontos de S constituídos de um R e um número ímpar: C={R1,R3,R5}.
2. (a) A ou B = AUB = {K2,K4,K6,K3,K5,R2,R3,R5}
(b) B e C = B ∩ C = {R3,R5}
(c) Escolhemos os elementos de B que não estão em A ou C;
B ∩ Ac ∩ Cc = {K3,K5,R2}
3. A e C são mutuamente exclusivos, porque A ∩ C = ∅
Conceito de probabilidade
Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de
ocorrer um evento A é:
14

15. Por, exemplo, no lançamento de um dado, um número par pode ocorrer de 3 maneiras diferentes dentre 6
igualmente prováveis, portanto, P = 3/6= 1/2 = 50%
Dizemos que um espaço amostral S (finito) é equiprovável quando seus eventos elementares têm
probabilidades iguais de ocorrência.
Num espaço amostral equiprovável S (finito), a probabilidade de ocorrência de um evento A é sempre:
Propriedades Importantes:
1. Se A e A’ são eventos complementares, então:
P( A ) + P( A' ) = 1
2. A probabilidade de um evento é sempre um número entre ∅ (probabilidade de evento impossível) e 1
(probabilidade do evento certo).
Probabilidade Condicional
Antes da realização de um experimento, é necessário que já tenha alguma informação sobre o evento que
se deseja observar. Nesse caso, o espaço amostral se modifica e o evento tem a sua probabilidade de
ocorrência alterada.
Fórmula de Probabilidade Condicional
P(E1 e E2 e E3 e ...e En-1 e En) é igual a P(E1).P(E2/E1).P(E3/E1 e E2)...P(En/E1 e E2 e ...En-1).
Onde P(E2/E1) é a probabilidade de ocorrer E2, condicionada pelo fato de já ter ocorrido E1;
P(E3/E1 e E2) é a probabilidade ocorrer E3, condicionada pelo fato de já terem ocorrido E1 e E2;
P(Pn/E1 e E2 e ...En-1) é a probabilidade de ocorrer En, condicionada ao fato de já ter ocorrido E1 e E2...En-1.
Exemplo:
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez
e sem reposição, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução:
Seja o espaço amostral S=30 bolas, e considerarmos os seguintes eventos:
A: vermelha na primeira retirada e P(A) = 10/30
B: azul na segunda retirada e P(B) = 20/29
Assim:
P(A e B) = P(A).(B/A) = 10/30.20/29 = 20/87
Eventos independentes
Dizemos que E1 e E2 e ...En-1, En são eventos independentes quando a probabilidade de ocorrer um deles
não depende do fato de os outros terem ou não terem ocorrido.
15

16. Fórmula da probabilidade dos eventos independentes:
P(E1 e E2 e E3 e ...e En-1 e En) = P(E1).P(E2).p(E3)...P(En)
Exemplo:
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a
sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução:
Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na
segunda retirada é igual ao produto das probabilidades de cada condição, ou seja, P(A e B) = P(A).P(B).
Ora, a probabilidade de sair vermelha na primeira retirada é 10/30 e a de sair azul na segunda retirada
20/30. Daí, usando a regra do produto, temos: 10/30.20/30=2/9.
Observe que na segunda retirada forma consideradas todas as bolas, pois houve reposição. Assim, P(B/A)
=P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que
ela foi reposta na urna.
Probabilidade de ocorrer a união de eventos
Fórmula da probabilidade de ocorrer a união de eventos:
P(E1 ou E2) = P(E1) + P(E2) - P(E1 e E2)
De fato, se existirem elementos comuns a E1 e E2, estes eventos estarão computados no cálculo de P(E1) e
P(E2). Para que sejam considerados uma vez só, subtraímos P(E1 e E2).
Fórmula de probabilidade de ocorrer a união de eventos mutuamente exclusivos:
P(E1 ou E2 ou E3 ou ... ou En) = P(E1) + P(E2) + ... + P(En)
Exemplo: Se dois dados, azul e branco, forem lançados, qual a probabilidade de sair 5 no azul e 3 no
branco?
Considerando os eventos:
A: Tirar 5 no dado azul e P(A) = 1/6
B: Tirar 3 no dado branco e P(B) = 1/6
Sendo S o espaço amostral de todos os possíveis resultados, temos:
n(S) = 6.6 = 36 possibilidades. Daí, temos:P(A ou B) = 1/6 + 1/6 – 1/36 = 11/36
Exemplo: Se retirarmos aleatoriamente uma carta de baralho com 52 cartas, qual a probabilidade de ser
um 8 ou um Rei?
Sendo S o espaço amostral de todos os resultados possíveis, temos: n(S) = 52 cartas. Considere os
eventos:
A: sair 8 e P(A) = 4/52
B: sair um rei e P(B) = 4/52
Assim, P(A ou B) = 4/52 + 4/52 – 0 = 8/52 = 2/13. Note que P(A e B) = 0, pois uma carta não pode ser 8 e
rei ao mesmo tempo. Quando isso ocorre dizemos que os eventos A e B são mutuamente exclusivos.
DEFINIÇÃO DE LOGARITMO
16

17. a x = b ⇔ x = log a b sendo b>0 ,a>0 e a≠1
Na igualdade x = log a b obtemos :
a= base do logaritmo
b= logaritmando ou antilogaritmo
x= logaritmo
Exemplos :
1) log 2 32 = 5 pois 2 5 = 32
2) log 4 16 = 2 pois 4 2 = 16
3) log 5 1 = 0 pois 5 0 = 1
Consequências da definição
Sendo b>0 ,a>0 e a≠1 e m um número real qualquer, temos a seguir algumas consequências da
definição de logaritmo:
log a 1 = 0 log a a = 1 log a a m = m a log a b = b
log a b = log a c ⇔ b = c
Propriedades operatórias dos logaritmos
1) Logaritmo do produto: log a ( x. y ) = log a x + log a y (a>0, a≠1, x>0 e y>0)
2) Logaritmo do quociente:  x (a>0, a≠1, x>0 e y>0)
log a   = log a x − log a y
 y
 
3) Logaritmo da potência: log a x m = m. log a x (a>0, a≠1, x>0 e m ∈ℜ)
m
n
x m
=x n
Caso particular: como , temos:
m
m
log a x = log a x =
n m n
. log a x
n
Cologaritmo
17

18. Chamamos de cologaritmo de um número positivo b numa base a (a>0, a≠1) e indicamos
cologa b o logaritmo inverso desse número b na base a
1
colog a b = log a (a>0, a≠1 e b>0)
b
1
Como log a = log a 1 − log a b = 0 − log a b = − log a b, podemos também escrever :
b
colog a b = − log a b
Mudança de base
Em algumas situações podemos encontrar no cálculo vários logaritmos em bases diferentes.
Como as propriedades logarítmicas só valem para logaritmos numa mesma base, é necessário fazer,
antes, a conversão dos logaritmos de bases diferentes para uma única base conveniente. Essa
conversão chama-se mudança de base. Para fazer a mudança de uma base a para uma outra base b
usa-se:
log b x
log a x =
log b a
MATRIZES E DETERMINANTES
18

19. 1) Dadas as matrizes :
 5 2  2 − 2 a b 
A=  , B = 0 1  e X =  c d  tais que 2 A − X = B, calcule o determinante de X .
− 1 1    
Primeiramente encontramos a matriz X :
5 2   a b  2 − 2 
2 − =
− 1 1   c d  0 1 
    
 10 4  a b   2 − 2
− 2 − =
 2  c d  0 1 
    
10 − a = 2 → a = 8
4 − b = −2 → b = 6
 10 − a 4 − b  2 − 2   8 6
 − 2 − c 2 − d  = 0 1  ⇒  ⇒ X = 
    − 2 − c = 0 → c = −2 − 2 1 
2 − d = 1 → d = 1

8 6
det X = = 8.1 − 6.(−2) = 8 + 12 = 20
−2 1
2 1 3
2) Encontre a solução da equação 4 − 1 n − 1 = 12.
n 0 n
Para achar o determinante de uma matriz 3x3 podemos utilizar a regra de Sarrus, que consiste em
copiar as duas primeiras colunas à direita da matriz, e subtrair a soma dos produtos da primeira
diagonal, pela soma dos produtos da segunda :
2 1 3 2 1
4 − 1 n − 1 4 − 1 = 12 ⇒ (−2n + n(n − 1) + 0) − ( −3n + 0 + 4n) = 12
n 0 n n 0
(−2n + n 2 − n) − n = 12 ⇒ n 2 − 4n − 12 = 0
4 ± 16-4.1.(-12 ) 4 ± 64 4±8 n = 6
n= ⇒ n= ⇒ n= ⇒
2 2 2  n = −2
 1 0
5 − 3
3) Sendo A = − 2 3 e B = 
   calcule AB.
 0 4 1 2 
 
Essa é uma questão de multiplicação de matrizes, onde estamos multiplicando uma matriz 3x2
por uma 2x2. O resultado será obtido pelo produto de cada linha da matriz A por cada coluna
da matriz B. O resultado será uma matriz 3x2.
 1.5 + 0.1 1.(−3) + 0.2   5 − 3
AB = (−2).5 + 3.1 (−2)(−3) + 3.2 ⇒ AB = − 7 12 
   
 0.5 + 4.1
 0(−3) + 4.2  4
 8
19

20. 4 5 
4) Sendo A =  , determine a matriz inversa da matriz A.
3 4
Sabemos que uma matriz multiplicada pela sua inversa resulta na matriz identidade, ou seja :
A. A −1 = I
4a + 5c = 1 4a + 5c = 1 a = 4
4b + 5d = 0  → 
4 5 a b  1 0  3a + 4c = 0 c = −3
3 4. c d  = 0 1 ⇒ 3a + 4c = 0 ⇒ 4b + 5d = 0 b = −5
      → 

3b + 4d = 1
 3b + 4d = 1 d = 4
 4 − 5
Portanto, a matriz inversa de A é A −1 =  
− 3 4 
O CONJUNTO DOS NÚMEROS COMPLEXOS
De números complexos você deve saber :
i 2 = −1
Conjugado de um número complexo : z = a + bi ⇔ z = a − bi
z1 z1 .z 2
Divisão de dois números complexos : =
z 2 z 2 .z 2
Módulo de um número complexo : z = a 2 + b 2
a b
Argumento de um número complexo : cos(θ ) = e sen(θ ) =
z z
Forma trigonométrica ou polar : z = z .(cos(θ ) + i. sen(θ ))
Multiplicação na forma trigonométrica : z1 .z 2 = z1 . z 2 .(cos(θ 1 + θ 2 ) + i. sen(θ 1 + θ 2 ))
z1 z1
Divisão na forma trigonométrica : = .(cos(θ 1 − θ 2 ) + i. sen(θ 1 − θ 2 ))
z2 z2
n
Potenciação na forma trigonométrica : z n = z .(cos(nθ ) + i. sen(nθ ))
20

21. Exercícios resolvidos
2+i
1) Calcule .
5 − 3i
Multiplicam - se ambos os termos da fração pelo número complexo conjugado do
denominador :
(2 + i ) (5 + 3i ) 10 + 6i + 5i + 3i 2 10 + 11i − 3 7 + 11i 7 11
. = = = = + i
(5 − 3i ) (5 + 3i ) 25 − 9i 2
25 − ( −9) 34 34 34
1− i i
2) Coloque na forma a + bi a expressão + .
1+ i i − 2
Em cada fração, multiplicamos seus termos pelo número complexo conjugado do
denominador :
(1 − i ) (1 − i ) i ( −2 − i ) 1 − 2i + i 2 − 2i − i 2 1 − 2i − 1 − 2i − (−1)
. + . = + = + =
(1 + i ) (1 − i ) (−2 + i ) (−2 − i ) 1− i 2
4−i 2
1 − (−1) 4 − (−1)
− 2i 1 − 2i 1 − 2i − 5i + 1 − 2i 1 − 7i 1 7
= + = −i+ = = = − i
2 5 5 5 5 5 5
21

22. 3) Calcule :
92 4 45 4
a) i 92
→ 92 23 → i =1
0
b) i 45
→ 44 11 → i1 = i
0 1
310 4 1081 4
c) i 310
→ 308 77 → i = −1 2
d) i 1081
→ 1080 270 → i 1 = i
2 1
e) i 4 n = i 4 = i 2 .i 2 = (−1).(−1) = 1 f) i 4 n +1 = i 4 n .i = 1.i = i
g) i 4 n + 2 = i 4 n .i 2 = 1.(−1) = −1 h) i 4 n + 3 = i 4 n .i 3 = 1.(−i ) = −i
(4 − 3i )(12 − 5i )
4) Ache o módulo do número complexo .
2i
Primeiramente colocamos o número na forma a + bi :
(4 − 3i )(12 − 5i ) (− 2i ) (48 − 20i − 36i + 15i 2 ).(− 2i ) (33 − 56i ).(− 2i )
. = = =
( 2i ) (− 2i ) − 2i 2
− 2(−1)
− 33 2i − 56 2 33 2
= = − 28 2 − i
2 2
Agora encontramos o módulo desse número complexo :
2
 33 2  2178 8450 4225
z = a + b = (−28 2 ) +  −
2

2
 = 1568 + =
2
= =
 2  4 4 2
65 2 65 2 65 2
= . = → z =
2 2 2 2
5) Obtenha o argumento dos números complexos a seguir :
a) z = 2 + 2 3i → z = 2 2 + (2 3 ) 2 = 4 + 12 = 16 = 4
a 2 1
cos(θ ) =  = =
z 4 2 π
 θ = 60 =
0
b 2 3 3  3
sen(θ ) = = =
z 4 2 
22

23. b) z = 4i → z = 0 2 + 4 2 = 16 = 4
a 0 
cos(θ ) = = =0 
z 4  π
 θ = 90 =
0
b 4 2
sen(θ ) = = = 1 
z 4 

6) Passe o número complexo z = 8i para a forma trigonométrica.
z = 0 2 + 8 2 = 64 = 8
a 0 
cos(θ ) = = =0 
z 8  π
 θ =
b 8 2
sen(θ ) = = = 1 
z 8 

Passando para a forma trigonométrica :
z = z .(cos(θ ) + i. sen(θ ))
 π   π 
z = 8. cos  + i. sen   
 
 2  2 
 π   π 
7) Dados z1 = 5(cos(π ) + i. sen(π )) e z 2 = 3. cos  + i. sen  , obtenha z1 .z 2 .
 
 3  3 
z1 = (5 cos(π )) 2 + (5 sen(π )) 2 = (−5) 2 + 0 2 = 25 = 5
2 2
  π    π  9 27 36
z 2 =  3 cos   +  3 sen    =
    + = = 9 =3
  3    3  4 4 4
a 3/ 2 1 
a −5  cos(θ 2 ) = = = 
cos(θ 1 ) = = = −1 z2 3 2
z1 5  
 π
 θ1 = π 3 3  θ2 =
b 0 3
sen(θ 1 ) = = =0  b 
2 = 3 
z1 5 
 sen(θ 2 ) = =
z2 3 2 

z1 .z 2 = z1 . z 2 .(cos(θ 1 + θ 2 ) + i. sen(θ 1 + θ 2 ))
  π  π 
z1 .z 2 = 5.3. cos π +  + i. sen  π +  

  3  3 

  4π   4π 
z1 .z 2 = 15. cos
  + i. sen  

  3   3 
23

24. POLINÔMIOS
• Definição
Uma função polinomial ou simplesmente polinômio, é toda função definida pela
relação P(x)=anxn + an-1.xn-1 + an-2.xn-2 + ... + a2x2 + a1x + a0.
Onde:
an, an-1, an-2, ..., a2, a1, a0 são números reais chamados coeficientes.
n ∈ IN
x ∈ C (nos complexos) é a variável.
GRAU DE UM POLINÔMIO:
Grau de um polinômio é o expoente máximo que ele possui. Se o coeficiente an≠0,
então o expoente máximo n é dito grau do polinômio e indicamos gr(P)=n. Exemplos:
a) P(x)=5 ou P(x)=5.x0 é um polinômio constante, ou seja, gr(P)=0.
b) P(x)=3x+5 é um polinômio do 1º grau, isto é, gr(P)=1.
c) P(x)=4x5+7x4 é um polinômio do 5º grau, ou seja, gr(P)=5.
Obs: Se P(x)=0, não se define o grau do polinômio.
• Valor numérico
O valor numérico de um polinômio P(x) para x=a, é o número que se obtém
substituindo x por a e efetuando todas as operações indicadas pela relação que define o
polinômio. Exemplo:
Se P(x)=x3+2x2+x-4, o valor numérico de P(x), para x=2, é:
P(x)= x3+2x2+x-4
P(2)= 23+2.22+2-4
P(2)= 14
Observação: Se P(a)=0, o número a chamado raiz ou zero de P(x).
Por exemplo, no polinômio P(x)=x2-3x+2 temos P(1)=0; logo, 1 é raiz ou zero desse
polinômio.
24

25. Alguns exercícios resolvidos:
1º) Sabendo-se que –3 é raiz de P(x)=x3+4x2-ax+1, calcular o valor de a.
Resolução: Se –3 é raiz de P(x), então P(-3)=0.
P(-3)=0 => (-3)3+4(-3)2-a.(-3)+1 = 0
3a = -10 => a=-10/3
Resposta: a=-10/3
2º) Calcular m ∈ IR para que o polinômio
P(x)=(m2-1)x3+(m+1)x2-x+4 seja:
a) do 3ºgrau b) do 2º grau c) do 1º grau
Resposta:
a) para o polinômio ser do 3º grau, os coeficientes de x2 e x3 devem ser diferentes de
zero. Então:
m2-1≠0 => m2≠1 => m≠1
m+1≠0 => m≠-1
Portanto, o polinômio é do 3º grau se m≠1 e m≠-1.
b) para o polinômio ser do 2º grau, o coeficiente de x3 deve ser igual a zero e o
coeficiente de x2 diferente de zero. Então:
m2-1=0 => m2=1 => m=±1
m+1≠0 => m≠-1
Portanto, o polinômio é do 2º grau se m=1.
c) para o polinômio ser do 1º grau, os coeficientes de x2 e x3 devem ser iguais a zero.
Então:
m2-1=0 => m2=1 => m=±1
m+1=0 => m=-1
Portanto, o polinômio é do 1º grau se m=-1.
25

26. 3º) Num polinômio P(x), do 3º grau, o coeficiente de x3 é 1. Se P(1)=P(2)=0 e P(3)=30,
calcule o valor de P(-1).
Resolução:
Temos o polinômio: P(x)=x3+ax2+bx+c.
Precisamos encontrar os valores de a,b e c (coeficientes).
Vamos utilizar os dados fornecidos pelo enunciado do problema:
P(1)=0 => (1)3+a.(1)2+b(1)+c = 0 => 1+a+b+c=0 => a+b+c=-1
P(2)=0 => (2)3+a.(2)2+b(2)+c = 0 => 8+4a+2b+c=0 => 4a+2b+c=-8
P(3)=30 => (3)3+a.(3)2+b(3)+c = 30 => 27+9a+3b+c=30 => 9a+3b+c=3
Temos um sistema de três variáveis:
a + b + c = -1

4a + 2b + c = -8
9a + 3b + c = 3

Resolvendo esse sistema encontramos as soluções:
a=9, b=-34, c=24
Portanto o polinômio em questão é P(x)= x3+9x2-34x+24.
O problema pede P(-1):
P(-1)= (-1)3+9(-1)2-34(-1)+24 => P(-1)=-1+9+34+24
P(-1)= 66
Resposta: P(-1)= 66
26

27. • Polinômios iguais
Dizemos que dois polinômios A(x) e B(x) são iguais ou idênticos (e indicamos
A(x)≡B(x)) quando assumem valores numéricos iguais para qualquer valor comum
atribuído à variável x. A condição para que dois polinômios sejam iguais ou idênticos é
que os coeficientes dos termos correspondentes sejam iguais.
Exemplo:
Calcular a,b e c, sabendo-se que x2-2x+1 ≡ a(x2+x+1)+(bx+c)(x+1).
Resolução: Eliminando os parênteses e somando os termos semelhantes do segundo
membro temos:
x2-2x+1 ≡ ax2+ax+a+bx2+bx+cx+c
1x2-2x+1 ≡ (a+b)x2+(a+b+c)x+(a+c)
Agora igualamos os coeficientes correspondentes:
a + b = 1

a + b + c = −2
a + c = 1

Substituindo a 1ª equação na 2ª:
1+c = -2 => c=-3.
Colocando esse valor de c na 3ª equação, temos:
a-3=1 => a=4.
Colocando esse valor de a na 1ª equação, temos:
4+b=1 => b=-3.
Resposta: a=4, b=-3 e c=-3.
Obs: um polinômio é dito identicamente nulo se tem todos os seus coeficientes
nulos.
27

28. • Divisão de polinômios
Sejam dois polinômios P(x) e D(x), com D(x) não nulo.
Efetuar a divisão de P por D é determinar dois polinômios Q(x) e R(x), que
satisfaçam as duas condições abaixo:
1ª) Q(x).D(x) + R(x) = P(x)
2ª) gr(R) < gr(D) ou R(x)=0
P( x) D( x )
R( x) Q( x)
Nessa divisão:
P(x) é o dividendo.
D(x) é o divisor.
Q(x) é o quociente.
R(x) é o resto da divisão.
Obs: Quando temos R(x)=0 dizemos que a divisão é exata, ou seja, P(x) é divisível
por D(x) ou D(x) é divisor de P(x).
Se D(x) é divisor de P(x) ⇔
R(x)=0
Exemplo:
Determinar o quociente de P(x)=x4+x3-7x2+9x-1 por D(x)=x2+3x-2.
Resolução: Aplicando o método da chave, temos:
x 4 + x3 − 7 x 2 + 9 x − 1 x 2 + 3x − 2
− x 4 − 3x3 + 2 x 2 x 2 − 2 x + 1 → Q( x)
− 2 x3 − 5x2 + 9 x − 1
+ 2 x3 + 6 x2 − 4 x
x2 + 5x − 1
− x 2 − 3x + 2
2 x + 1 → R ( x)
Verificamos que:
x 4  -  1 ≡ (x 2 + 3x - 2) (x 2 - 2x + 1) + (2x + 1)
 + x 7x + 9x
3 2
-
    
P(x) D(x) Q(x) R(x)
28

29. • Divisão de um polinômio por um binômio da forma ax+b
Vamos calcular o resto da divisão de P(x)=4x2-2x+3 por D(x)=2x-1.
Utilizando o método da chave temos:
4 x2 − 2 x + 3 2x − 1
− 4 x2 + 2 x 2x
3
Logo: R(x)=3
A raiz do divisor é 2x-1=0 => x=1/2.
Agora calculamos P(x) para x=1/2.
P(1/2) = 4(1/4) – 2(1/2) + 3
P(1/2) = 3
Observe que R(x) = 3 = P(1/2)
Portanto, mostramos que o resto da divisão de P(x) por D(x) é igual ao valor
numérico de P(x) para x=1/2, isto é, a raiz do divisor.
• Teorema do resto
O resto da divisão de um polinômio P(x) pelo binômio ax+b é igual a P(-b/a).
Note que –b/a é a raiz do divisor.
Exemplo: Calcule o resto da divisão de x2+5x-1 por x+1.
Resolução: Achamos a raiz do divisor:
x+1=0 => x=-1
Pelo teorema do resto sabemos que o resto é igual a P(-1):
P(-1)=(-1)2+5.(-1)-1 => P(-1) = -5 = R(x)
Resposta: R(x) = -5.
• Teorema de D’Alembert
Um polinômio P(x) é divisível pelo binômio ax+b se P(-b/a)=0
Exemplo: Determinar o valor de p, para que o polinômio P(x)=2x3+5x2-px+2 seja
divisível por x-2.
Resolução: Se P(x) é divisível por x-2, então P(2)=0.
P(2)=0 => 2.8+5.4-2p+2=0 => 16+20-2p+2=0 => p=19
Resposta: p=19.
29

30. • Divisão de um polinômio pelo produto (x-a)(x-b)
Vamos resolver o seguinte problema: calcular o resto da divisão do polinômio P(x)
pelo produto (x-a)(x-b), sabendo-se que os restos da divisão de P(x) por (x-a) e por (x-b)
são, respectivamente, r1 e r2.
Temos:
a é a raiz do divisor x-a, portanto P(a)=r1 (eq. 1)
b é a raiz do divisor x-b, portanto P(b)=r2 (eq. 2)
E para o divisor (x-a)(x-b) temos P(x)=(x-a)(x-b) Q(x) + R(x) (eq. 3)
O resto da divisão de P(x) por (x-a)(x-b) é no máximo do 1º grau, pois o divisor é do
2º grau; logo:
R(x)=cx+d
Da eq.3 vem:
P(x)=(x-a)(x-b) Q(x) + cx + d
Fazendo:
x=a => P(a) = c(a)+d (eq. 4)
x=b => P(b) = c(b)+d (eq. 5)
Das equações 1, 2, 4 e 5 temos:
ca + d = r1

cb + d = r2
Resolvendo o sistema obtemos:
r1 − r2 ar − ar1
c= e d= 2 , com a ≠ b
a−b a−b
r −r ar − ar1
Logo : R ( x) = 1 2 x + 2 , com a ≠ b
a−b a−b
Observações:
1ª) Se P(x) for divisível por (x-a) e por (x-b), temos:
P(a)= r1 =0
P(b)= r2 =0
Portanto, P(x) é divisível pelo produto (x-a)(x-b), pois:
r1 − r2 ar − ar1
R( x) = x+ 2 = 0+0 = 0
a −b a−b
30

31. 2ª) Generalizando, temos:
Se P(x) é divisível por n fatores distintos (x-a1), (x-a2),..., (x-an) então P(x) é
divisível pelo produto (x-a1)(x-a2)...(x-an).
Exemplo:
Um polinômio P(x) dividido por x dá resto 6 e dividido por (x-1) dá resto 8. Qual o
resto da divisão de P(x) por x(x-1)?
Resolução:
0 é a raiz do divisor x, portanto P(0)=6 (eq. 1)
1 é a raiz do divisor x-1, portanto P(1)=8 (eq. 2)
E para o divisor x(x-1) temos P(x)=x(x-1) Q(x) + R(x) (eq. 3)
O resto da divisão de P(x) por x(x-1) é no máximo do 1º grau, pois o divisor é do 2º
grau; logo:
R(x)=ax+b
Da eq.3 vem:
P(x)=x(x-1) Q(x) + ax + b
Fazendo:
x=0 => P(0) = a(0)+b => P(0) = b (eq. 4)
x=1 => P(1) = a(1)+b => P(1) = a+b (eq. 5)
Das equações 1, 2, 4 e 5 temos:
b = 6

a + b = 8
Logo, b=6 e a=2.
Agora achamos o resto: R(x) = ax+b = 2x+6
Resposta: R(x) = 2x+6.
31

32. • O dispositivo de Briot-Ruffini
Serve para efetuar a divisão de um polinômio P(x) por um binômio da forma (ax+b).
Exemplo: Determinar o quociente e o resto da divisão do polinômio
P(x)=3x3-5x2+x-2 por (x-2).
Resolução:
RAIZ DO DIVISOR

  ES DE P(x) 
COEFICIENT
  
2 3 −5 1 −2
↓ 3.(2) − 5 1.( 2) + 1 3.( 2) − 2
1 
3  3
  4

COEFICIENTES DO QUOCIENTE Q(x) RESTO
Observe que o grau de Q(x) é uma unidade inferior ao de P(x), pois o divisor é de
grau 1.
Resposta: Q(x)=3x2+x+3 e R(x)=4.
Para a resolução desse problema seguimos os seguintes passos:
1º) Colocamos a raiz do divisor e os coeficientes do dividendo ordenadamente na
parte de cima da “cerquinha”.
2º) O primeiro coeficiente do dividendo é repetido abaixo.
3º) Multiplicamos a raiz do divisor por esse coeficiente repetido abaixo e somamos o
produto com o 2º coeficiente do dividendo, colocando o resultado abaixo deste.
4º) Multiplicamos a raiz do divisor pelo número colocado abaixo do 2º coeficiente e
somamos o produto com o 3º coeficiente, colocando o resultado abaixo deste, e assim
sucessivamente.
5º) Separamos o último número formado, que é igual ao resto da divisão, e os
números que ficam à esquerda deste serão os coeficientes do quociente.
32

33. • Decomposição de um polinômio em fatores
Vamos analisar dois casos:
1º caso: O polinômio é do 2º grau.
De uma forma geral, o polinômio de 2º grau P(x)=ax2+bx+c que admite as raízes
r1 e r2 pode ser decomposto em fatores do 1º grau, da seguinte forma:
ax2+bx+c = a(x-r1)(x-r2)
Exemplos:
1) Fatorar o polinômio P(x)=x2-4.
Resolução: Fazendo x2-4=0, obtemos as raízes r1=2 e r2=-2.
Logo: x2-4 = (x-2)(x+2).
2) Fatorar o polinômio P(x)=x2-7x+10.
Resolução: Fazendo x2-7x+10=0, obtemos as raízes r1=5 e r2=2.
Logo: x2-7x+10 = (x-5)(x-2).
2º caso: O polinômio é de grau maior ou igual a 3.
Conhecendo uma das raízes de um polinômio de 3º grau, podemos decompô-lo
num produto de um polinômio do 1º grau por um polinômio do 2º grau e, se este tiver
raízes, podemos em seguida decompô-lo também.
Exemplo: Decompor em fatores do 1º grau o polinômio 2x3-x2-x.
Resolução:
2x3-x2-x = x.(2x2-x-1)  colocando x em evidência
Fazendo x.(2x2-x-1) = 0 obtemos: x=0 ou 2x2-x-1=0.
Uma das raízes já encontramos (x=0).
As outras duas saem da equação: 2x2-x-1=0 => r1=1 e r2=-1/2.
Portanto, o polinômio 2x3-x2-x, na forma fatorada é:
2.x.(x-1).(x+(1/2)).
Generalizando, se o polinômio P(x)=anxn+an-1xn-1+...+a1x+a0 admite n raízes r1, r2,..., rn,
podemos decompô-lo em fatores da seguinte forma:
anxn+an-1xn-1+...+a1x+a0 = an(x-r1)(x-r2)...(x-rn)
Observações:
1) Se duas, três ou mais raiz forem iguais, dizemos que são raízes duplas, triplas,
etc.
2) Uma raiz r1 do polinômio P(x) é dita raiz dupla ou de multiplicidade 2 se P(x)
é divisível por (x-r1)2 e não por (x-r1)3.
33

34. PRODUTOS NOTÁVEIS
É muito comum nas expressões algébrica o aparecimento de certos produtos. Para
simplificar o trabalho nos cálculos será muito útil a aplicação dos produtos notáveis.
Veja a tabela abaixo:
Produtos notáveis Exemplos
2 2 2 2 2
(a+b) = a +2ab+b (x+3) = x +6x+9
(a-b)2 = a2-2ab+b2 (x-3)2 = x2-6x+9
(a+b)(a-b) = a2-b2 (x+3)(x-3) = x2-9
(x+a)(x+b) = x2+(a+b)x+ab (x+2)(x+3) = x2+5x+6
(a+b)3 = a3+3a2b+3ab2+b3 (x+2)3 = x3+6x2+12x+8
(a-b)3 = a3-3a2b+3ab2-b3 (x-2)3 = x3-6x2+12x-8
(a+b)(a2-ab+b2) = a3+b3 (x+2)(x2-2x+4) = x3+8
(a-b)(a2+ab+b2) = a3-b3 (x-2)(x2+2x+4) = x3-8
ALGUNS EXERCÍCIOS RESOLVIDOS:
1) Desenvolva:
a) (3x+y)2
(3x+y)2 = (3x)2+2.3x.y+y2 = 9x2+6xy+y2
b) ((1/2)+x2)2
((1/2)+x2)2 = (1/2)2+2.(1/2).x2+(x2)2 = (1/4) +x2+x4
c) ((2x/3)+4y3)2
((2x/3)+4y3)2 = (2x/3)2-2.(2x/3).4y3+(4y3)2= (4/9)x2-(16/3)xy3+16y6
d) (2x+3y)3
(2x+3y)3 = (2x)3+3.(2x)2.3y+3.2x.(3y)2+(3y)3 = 8x3+36x2y+54xy2+27y3
e) (x4+(1/x2))3
(x4+(1/x2))3 = (x4)3+3.(x4)2.(1/x2)+3.x4.(1/x2)2+(1/x2)3 = x12+3x6+3+(1/x6)
f) ((2x/3)+(4y/5)).((2x/3)-(4y/5))
((2x/3)+(4y/5)).((2x/3)-(4y/5)) = (2x/3)2-(4y/5)2 = (4/9)x2-(16/25)y2
2) Efetue as multiplicações:
a) (x-2)(x-3)
(x-2)(x-3) = x2+((-2)+(-3))x+(-2).(-3) = x2-5x+6
b) (x+5)(x-4)
(x+5)(x-4) = x2+(5+(-4))x+5.(-4) = x2+x-20
34

35. 3) Simplifique as expressões:
a) (x+y)2–x2-y2
(x+y)2–x2-y2 = x2+2xy+y2–x2-y2 = 2xy
b) (x+2)(x-7)+(x-5)(x+3)
(x+2)(x-7)+(x-5)(x+3) = x2+(2+(-7))x+2.(-7) + x2+(-5+3)x+3.(-5) =
x2-5x-14+ x2-2x-15 = 2x2-7x-29
c) (2x-y)2-4x(x-y)
(2x-y)2-4x(x-y) = (2x)2-2.2x.y+y2-4x2+4xy = 4x2-4xy+y2-4x2+4xy = y2
35

36. Progressões Aritméticas
Progressão aritmética é uma sequência numérica na qual, a partir do segundo, cada termo é
igual à soma de seu antecessor com uma constante, denominada razão.
Fórmula do termo geral de uma P.A. : a n = a1 + (n − 1).r
(a1 + a n ).n
Soma de termos de uma P.A. finita : S n =
2
Logo abaixo temos alguns exercícios de progressões aritméticas resolvidos.
1) Dada a P.A. (-19,-15,-11,...) calcule o seu enésimo termo.
Primeiramente encontramos a razão : r = a2 − a1 ⇒ r = −15 − (−19) ⇒ r = 4.
Logo, o termo geral é :
an = a1 + (n − 1).r ⇒ an = −19 + (n − 1).4 ⇒ an = −19 + 4n − 4 ⇒ an = 4n − 23
2) Interpole seis meios aritméticos entre –8 e 13.
No problema : a1 = −8, an = 13, n = 8 (pois 6 meios aritméticos serão interpolados
entre os dois extremos, que são - 8 e 13. Logo, existem 8 termos na P.A.).
Para interpolar os valores, devemos encontrar a razão :
an = a1 + (n − 1).r ⇒ 13 = −8 + (8 − 1).r ⇒ 13 = −8 + 7 r ⇒ 13 + 8 = 7 r ⇒
21
7r = 21 ⇒ r = ⇒ r = 3.
7
Encontrada a razão, basta interpolar os meios aritméticos :
- 8, - 5, - 2, 1, 4, 7, 10, 13
36

37. 3) Escreva uma P.A. de três termos, sabendo que a soma desses termos vale 12 e que a
soma de seus quadrados vale 80.
a1 + a 2 + a 3 = 12

 2
a1 + a 2 2 + a3 2 = 80

Sabemos que a 2 = a1 + r e que a 3 = a1 + 2r. Então substituimos no sistema acima :
a1 + (a1 + r ) + (a1 + 2r ) = 12 3a1 + 3r = 12
 2 ⇒  2 2 2
⇒
a1 + (a1 + r ) + (a1 + 2r ) = 80 a1 + a1 + 2a1 r + r + a1 + 4a1 r + 4r = 80
2 2 2 2
 12 − 3r
3a1 + 3r = 12 → a1 = → a1 = 4 − r
⇒  3
3a 2 + 6a r + 5r 2 = 80
 1 1
Substituindo na segunda equação temos :
3(4 − r ) 2 + 6(4 − r )r + 5r 2 = 80
3(16 − 8r + r 2 ) + (24 − 6r )r + 5r 2 = 80
48 − 24r + 3r 2 + 24r − 6r 2 + 5r 2 = 80
48 + 2r 2 = 80 → 2r 2 = 80 − 48 → 2r 2 = 32 → r 2 = 16 → r = 16 → r = ±4
Agora encontramos o primeiro termo :
1) Para r = 4 :
a1 = 4 - r → a 1 = 4 - 4 → a 1 = 0
P.A : (0,4,8)
1) Para r = −4 :
a1 = 4 - r → a 1 = 4 - (-4) → a 1 = 8
P.A : (8,4,0)
Resposta : (0,4,8) ou (8,4,0).
4) Calcule quantos números inteiros existem entre 13 e 247 que não são múltiplos de 3.
Entre 13 e 247 existem 233 números. Para calcular quantos números NÃO são múltiplos de 3,
nós devemos calcular primeiramente quantos números SÃO múltiplos de 3, e logo após subtrair o número
total de números (233) pelo número de múltiplos, o que dará como resultado o número de NÃO múltiplos.
Para calcular o número de múltiplos de 3 :
a1 = 15 (pois é o primeiro múltiplo de 3 depois do 13)
r = 3, a n = 246 (pois é o último múltiplo de 3 antes do 247). Basta achar o n, que é o número de múltiplos :
234
a n = a1 + (n − 1).r → 246 = 15 + (n - 1)3 → 231 = 3n - 3 → n = → n = 78
3
Dos 233 números, 78 são múltiplos de 3, logo 155 não são múltiplos de 3.
37

38. 5) Encontre o valor de x para que a sequência (2x, x+1, 3x) seja uma progressão aritmética.
Para ser uma P.A. : a3 − a 2 = a 2 − a1
3 x − ( x + 1) = ( x + 1) − 2 x
2x − 1 = 1 − x
2
2x + x = 1 + 1 → 3x = 2 → x=
3
6) Numa progressão aritmética em que a2+a7=a4+ak, o valor de k é:
(a1 + r ) + (a1 + 6r ) = (a1 + 3r ) + a k
2a1 + 7 r = a1 + 3r + a k
2a1 − a1 + 7 r − 3r = a k → a k = a1 + 4r
Logo k = 5, pois a5 = a1 + 4r.
7) Se Sn é a soma dos n primeiros termos da progressão aritmética (-90,-86,-82,...) então o
menor valor de n para que se tenha Sn>0 é:
r = 4

Pelo enunciado, obtemos os seguintes dados : a1 = −90
a = 94 (pois a S deve ser maior que zero)
 n n
Basta encontrar o número de termos :
a n = a1 + (n − 1).r
94 = −90 + (n − 1).4
94 + 90 = 4n − 4
188
184 + 4 = 4n → n = → n = 47
4
8) A soma dos n primeiros números pares positivos é 132. Encontre o valor de n.
r = 2 ; a1 = 2 ; S n = 132
a n = a1 + (n − 1).r → a n = 2 + (n − 1).2 → a n = 2 + 2n − 2 → a n = 2n
Substituindo na fórmula da soma temos :
( a + a n ).n ( 2 + 2n) n
Sn = 1 → 132 = → n 2 + n − 132 = 0
2 2
− 1 ± 1 + 4.1.132 − 1 ± 529 − 1 ± 23 n = −12
n= = = = ⇒ n = 11
2 2 2 n = 11
PROGRESSÕES GEOMÉTRICAS
38

39. Podemos definir progressão geométrica, ou simplesmente P.G., como uma sucessão de
números reais obtida, com exceção do primeiro, multiplicando o número anterior por uma
quantidade fixa q, chamada razão.
Podemos calcular a razão da progressão, caso ela não esteja suficientemente evidente,
dividindo entre si dois termos consecutivos. Por exemplo, na sucessão (1, 2, 4, 8,...), q = 2.
Cálculos do termo geral
Numa progressão geométrica de razão q, os termos são obtidos, por definição, a
partir do primeiro, da seguinte maneira:
a1 a2 a3 ... a20 ... an ...
a1 a1xq a1xq2 ... a1xq19 a1xqn-1 ...
Assim, podemos deduzir a seguinte expressão do termo geral, também chamado
enésimo termo, para qualquer progressão geométrica.
an = a1 x qn-1
Portanto, se por exemplo, a1 = 2 e q = 1/2, então:
an = 2 x (1/2)n-1
Se quisermos calcular o valor do termo para n = 5, substituindo-o na fórmula, obtemos:
a5 = 2 x (1/2)5-1 = 2 x (1/2)4 = 1/8
A semelhança entre as progressões aritméticas e as geométricas é aparentemente
grande. Porém, encontramos a primeira diferença substancial no momento de sua definição.
Enquanto as progressões aritméticas formam-se somando-se uma mesma quantidade de
forma repetida, nas progressões geométricas os termos são gerados pela multiplicação,
também repetida, por um mesmo número. As diferenças não param aí.
Observe que, quando uma progressão aritmética tem a razão positiva, isto é, r > 0,
cada termo seu é maior que o anterior. Portanto, trata-se de uma progressão crescente. Ao
contrário, se tivermos uma progressão aritmética com razão negativa, r < 0, seu
comportamento será decrescente. Observe, também, a rapidez com que a progressão
cresce ou diminui. Isto é conseqüência direta do valor absoluto da razão, |r|. Assim, quanto
maior for r, em valor absoluto, maior será a velocidade de crescimento e vice-versa.
Soma dos n primeiros termos de uma PG
Seja a PG (a1, a2, a3, a4, ... , an , ...) .
Para o cálculo da soma dos n primeiros termos Sn,
Vamos considerar o que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Multiplicando ambos os membros pela razão q vem:
Sn.q = a1 . q + a2 .q + .... + an-1 . q + an .q
Conforme a definição de PG, podemos reescrever a expressão como:
Sn . q = a2 + a3 + ... + an + an . q
39

40. Observe que a2 + a3 + ... + an é igual a Sn - a1 . Logo, substituindo, vem:
S n . q = S n - a1 + a n . q
Daí, simplificando convenientemente, chegaremos à seguinte fórmula da soma:
Se substituirmos an = a1 . qn-1 , obteremos uma nova apresentação para a fórmula da
soma, ou seja:
Exemplo:
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Observe que neste caso a1 = 1.
• Soma dos termos de uma PG decrescente e ilimitada
Considere uma PG ILIMITADA ( infinitos termos) e decrescente. Nestas condições, podemos
considerar que no limite teremos an = 0. Substituindo na fórmula anterior, encontraremos:
Exemplo:
Resolva a equação: x + x/2 + x/4 + x/8 + x/16 + ... =100
O primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na
fórmula, vem:
Dessa equação encontramos como resposta x = 50.
40

41. IDENTIDADES TRIGONOMÉTRICAS
sen( x) π
1) tg ( x) = Relação válida para todo x ≠ + kπ
cos( x) 2
cos( x)
2) cot g ( x) = Relação válida para todo x ≠ kπ
sen( x)
1 π
3) sec( x) = Relação válida para todo x ≠ + kπ
cos( x) 2
1
4) cos ec( x) = Relação válida para todo x ≠ kπ
sen( x)
5) sen 2 ( x) + cos 2 ( x) = 1
Fórmulas da Adição
6) sen(a + b) = sen(a). cos(b) + sen(b). cos(a )
7) sen(a − b) = sen(a). cos(b) − sen(b). cos(a )
8) cos(a + b) = cos(a). cos(b) − sen(a). sen(b)
9) cos(a − b) = cos(a ). cos(b) + sen(a). sen(b)
 π
 p/ a ≠ + kπ
2
tg (a ) + tg (b) 
 π
10) tg ( a + b) =  p/ b ≠ + kπ
1 − tg (a).tg (b)  2
p/ (a + b) ≠ π + kπ

 2
 π
 p/ a ≠ + kπ
2
tg (a) − tg (b) 
 π
11) tg ( a − b) =  p/ b ≠ + kπ
1 + tg (a).tg (b)  2
p/ (a − b) ≠ π + kπ

 2
As fórmulas acima são verdadeiras para arcos positivos, cuja soma
pertence ao primeiro quadrante.
41

42. Fórmulas da Multiplicação
12) sen(2 x) = 2. sen( x). cos( x)
13) cos(2 x) = cos 2 ( x) − sen 2 ( x)
2.tg ( x)
14) tg (2 x) =
1 − tg 2 ( x)
Fórmulas da Transformação em Produto
x+ y x− y
15) sen( x) + sen( y ) = 2. sen  . cos 
 2   2 
x− y x+ y
16) sen(x) - sen(y) = 2. sen . cos 
 2   2 
x+ y x− y
17) cos( x) + cos( y ) = 2. cos . cos 
 2   2 
x+ y x− y
18) cos( x) − cos( y ) = −2. sen . sen 
 2   2 
42

43. FUNÇÃO DE 1º GRAU
Definição
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei
da forma f(x) = ax + b, onde a e b são números reais dados e a 0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Veja alguns exemplos de funções polinomiais do 1º grau:
f(x) = 5x - 3, onde a = 5 e b = - 3
f(x) = -2x - 7, onde a = -2 e b = - 7
f(x) = 11x, onde a = 11 e b = 0
Gráfico
O gráfico de uma função polinomial do 1º grau, y = ax + b, com a 0, é uma reta oblíqua aos eixos Ox e Oy.
Exemplo:
Vamos construir o gráfico da função y = 3x - 1:
Como o gráfico é uma reta, basta obter dois de seus pontos e ligá-los com o auxílio de uma régua:
a) Para x = 0, temos y = 3 · 0 - 1 = -1; portanto, um ponto é (0, -1).
b) Para y = 0, temos 0 = 3x - 1; portanto, e outro ponto é .
Marcamos os pontos (0, -1) e no plano cartesiano e ligamos os dois com uma reta.
x y
0 -1
0
Já vimos que o gráfico da função afim y = ax + b é uma reta.
O coeficiente de x, a, é chamado coeficiente angular da reta e, como veremos adiante, a está ligado à
inclinação da reta em relação ao eixo Ox.
O termo constante, b, é chamado coeficiente linear da reta. Para x = 0, temos y = a · 0 + b = b. Assim, o
coeficiente linear é a ordenada do ponto em que a reta corta o eixo Oy.
43

44. Zero e Equação do 1º Grau
Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a 0, o número real x
tal que f(x) = 0.
Temos:
f(x) = 0 ax + b = 0
Vejamos alguns exemplos:
1. Obtenção do zero da função f(x) = 2x - 5:
f(x) = 0 2x - 5 = 0
2. Cálculo da raiz da função g(x) = 3x + 6:
g(x) = 0 3x + 6 = 0 x = -2
3. Cálculo da abscissa do ponto em que o gráfico de h(x) = -2x + 10 corta o eixo das
abicissas:
O ponto em que o gráfico corta o eixo dos x é aquele em que h(x) = 0; então:
h(x) = 0 -2x + 10 = 0 x=5
Crescimento e decrescimento
Consideremos a função do 1º grau y = 3x - 1. Vamos atribuir valores cada vez maiores a x
e observar o que ocorre com y:
44

45. x -3 -2 -1 0 1 2 3
y -10 -7 -4 -1 2 5 8
Notemos que, quando aumentos o valor de x, os correspondentes valores de y também
aumentam. Dizemos, então que a
função y = 3x - 1 é crescente.
Observamos novamente seu gráfico:
Regra geral:
a função do 1º grau f(x) = ax + b é crescente quando o coeficiente de x é positivo (a > 0);
a função do 1º grau f(x) = ax + b é decrescente quando o coeficiente de x é negativo (a < 0);
Justificativa:
• para a > 0: se x1 < x2, então ax1 < ax2. Daí, ax1 + b < ax2 + b, de onde vem f(x1) < f(x2).
• para a < 0: se x1 < x2, então ax1 > ax2. Daí, ax1 + b > ax2 + b, de onde vem f(x1) > f(x2).
Sinal
Estudar o sinal de uma qualquer y = f(x) é determinar os valor de x para os quais y é positivo, os valores de x
para os quais y é zero e os valores de x para os quais y é negativo.
Consideremos uma função afim y = f(x) = ax + b vamos estudar seu sinal. Já vimos que essa função se
anula pra raiz . Há dois casos possíveis:
45

46. 1º) a > 0 (a função é crescente)
y>0 ax + b > 0 x>
y<0 ax + b < 0 x<
Conclusão: y é positivo para valores de x maiores que a raiz; y é negativo para valores de x menores que a
raiz
2º) a < 0 (a função é decrescente)
y>0 ax + b > 0 x<
y<0 ax + b < 0 x>
Conclusão: y é positivo para valores de x menores que a raiz; y é negativo para valores de x maiores que a
raiz.
46

47. FUNÇÃO QUADRÁTICA
Definição
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em
IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 0.
Vejamos alguns exemplos de função quadráticas:
1. f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
2. f(x) = x2 -1, onde a = 1, b = 0 e c = -1
3. f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
4. f(x) = - x2 + 8x, onde a = 1, b = 8 e c = 0
5. f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a 0, é uma curva
chamada parábola.
Exemplo:
Vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e,
em seguida, ligamos os pontos assim obtidos.
47

48. x y
-3 6
-2 2
-1 0
0 0
1 2
2 6
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
• se a > 0, a parábola tem a concavidade voltada para cima;
• se a < 0, a parábola tem a concavidade voltada para baixo;
Zero e Equação do 2º Grau
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a 0, os
números reais x tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 +
bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
Temos:
Observação
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o
radicando , chamado discriminante, a saber:
48

49. • quando é positivo, há duas raízes reais e distintas;
• quando é zero, há só uma raiz real;
• quando é negativo, não há raiz real.
Função Quadrática
Coordenadas do vértice da parábola
Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V;
quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V.
Em qualquer caso, as coordenadas de V são . Veja os gráficos:
49

50. Imagem
O conjunto-imagem Im da função y = ax2 + bx + c, a 0, é o conjunto dos valores que y
pode assumir. Há duas possibilidades:
1ª - quando a > 0,
50

51. a>0
2ª quando a < 0,
a<0
Construção da Parábola
É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares
(x, y), mas seguindo apenas o roteiro de observação seguinte:
1. O valor do coeficiente a define a concavidade da parábola;
51

52. 2. Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
3. O vértice V indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
4. A reta que passa por V e é paralela ao eixo dos y é o eixo de simetria da parábola;
5. Para x = 0 , temos y = a · 02 + b · 0 + c = c; então (0, c) é o ponto em que a parábola
corta o eixo dos y.
Sinal
Consideramos uma função quadrática y = f(x) = ax2 + bx + c e determinemos os valores de
x para os quais y é negativo e os valores de x para os quais y é positivos.
Conforme o sinal do discriminante = b2 - 4ac, podemos ocorrer os seguintes casos:
1º - > 0
Nesse caso a função quadrática admite dois zeros reais distintos (x1 x2). a parábola
intercepta o eixo Ox em dois pontos e o sinal da função é o indicado nos gráficos abaixo:
quando a > 0 quando a < 0
y>0 (x < x1 ou x > x2) y>0 x1 < x < x2
y<0 x1 < x < x2 y<0 (x < x1 ou x > x2)
2º - =0
52

53. quando a > 0 quando a < 0
3º - <0
quando a > 0 quando a < 0
EQUAÇÕES EXPONENCIAIS
53

54. Chamamos de equações exponenciais toda equação na qual a incógnita aparece
em expoente.
Exemplos de equações exponenciais:
1) 3x =81 (a solução é x=4)
2) 2x-5=16 (a solução é x=9)
3) 16x-42x-1-10=22x-1 (a solução é x=1)
4) 32x-1-3x-3x-1+1=0 (as soluções são x’=0 e x’’=1)
Para resolver equações exponenciais, devemos realizar dois passos importantes:
1º) redução dos dois membros da equação a potências de mesma base;
2º) aplicação da propriedade:
a m = a n ⇒ m = n (a ≠ 1 e a > 0)
EXERCÍCIOS RESOLVIDOS:
1) 3x=81
Resolução: Como 81=34, podemos escrever 3x = 34
E daí, x=4.
2) 9x = 1
Resolução: 9x = 1 ⇒ 9x = 90 ; logo x=0.
x
3 81
3)   =
4 256
x x x 4
3 81 3 34 3 3
Resolução :   = ⇒   = 4 ⇒   =   ; então x = 4.
4 256 4 4 4 4
4) 3 x = 4 27
3
3
Resolução : 3 = 27 ⇒ 3 = 3 ⇒ 3 = 3 ; logo x =
x 4 x 4 3 x 4
4
5) 23x-1 = 322x
Resolução: 23x-1 = 322x ⇒ 23x-1 = (25)2x ⇒ 23x-1 = 210x ; daí 3x-1=10,
de onde x=-1/7.
6) Resolva a equação 32x–6.3x–27=0.
54

55. Resolução: vamos resolver esta equação através de uma transformação:
32x–6.3x–27=0 ⇒ (3x)2-6.3x–27=0
Fazendo 3x=y, obtemos:
y2-6y–27=0 ; aplicando Bhaskara encontramos ⇒ y’=-3 e y’’=9
Para achar o x, devemos voltar os valores para a equação auxiliar 3x=y:
y’=-3 ⇒ 3x’ = -3 ⇒ não existe x’, pois potência de base positiva é positiva
y’’=9 ⇒ 3x’’ = 9 ⇒ 3x’’ = 32 ⇒ x’’=2
Portanto a solução é x=2
FUNÇÃO EXPONENCIAL
Chamamos de funções exponenciais aquelas nas quais temos a variável
aparecendo em expoente.
A função f:IRIR+ definida por f(x)=ax, com a ∈ IR+ e a≠1, é chamada função
exponencial de base a. O domínio dessa função é o conjunto IR (reais) e o
contradomínio é IR+ (reais positivos, maiores que zero).
GRÁFICO CARTESIANO DA FUNÇÃO EXPONENCIAL
Temos 2 casos a considerar:
 quando a>1;
 quando 0<a<1.
Acompanhe os exemplos seguintes:
1) y=2x (nesse caso, a=2, logo a>1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos
a tabela e o gráfico abaixo:
x -2 -1 0 1 2
y 1/4 1/2 1 2 4
2) y=(1/2)x (nesse caso, a=1/2, logo 0<a<1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos
a tabela e o gráfico abaixo:
55

56. x -2 -1 0 1 2
y 4 2 1 1/2 1/4
Nos dois exemplos, podemos observar que
a) o gráfico nunca intercepta o eixo horizontal; a função não tem raízes;
b) o gráfico corta o eixo vertical no ponto (0,1);
c) os valores de y são sempre positivos (potência de base positiva é positiva),
portanto o conjunto imagem é Im=IR+.
Além disso, podemos estabelecer o seguinte:
a>1 0<a<1
f(x) é crescente e Im=IR+ f(x) é decrescente e Im=IR+
Para quaisquer x1 e x2 do domínio: Para quaisquer x1 e x2 do domínio:
x2>x1 ⇒ y2>y1 (as desigualdades têm x2>x1 ⇒ y2<y1 (as desigualdades têm
mesmo sentido) sentidos diferentes)
INEQUAÇÕES EXPONENCIAIS
Chamamos de inequações exponenciais toda inequação na qual a incógnita
aparece em expoente.
56

57. Exemplos de inequações exponenciais:
1) 3 x > 81 (a solução é x > 4)
2
−1
2) 2 2x -2 ≤ 2 x (que é satisfeita para todo x real)
x −3
4 4
3)   ≥   (que é satisfeita para x ≤ -3)
5 5
4) 25 x - 150.5 x + 3125 < 0 (que é satisfeita para 2 < x < 3)
Para resolver inequações exponenciais, devemos realizar dois passos importantes:
1º) redução dos dois membros da inequação a potências de mesma base;
2º) aplicação da propriedade:
a>1 0<a<1
a > a ⇒ m>n
m n
a > an ⇒ m<n
m
(as desigualdades têm mesmo sentido) (as desigualdades têm sentidos
diferentes)
EXERCÍCIO RESOLVIDO:
− 11
1) 4 x −1 + 4 x − 4 x +1 >
4
Resolução :
4x − 11
A inequação pode ser escrita + 4 x − 4 x .4 > .
4 4
Multiplicando ambos os lados por 4 temos :
4 x + 4.4 x − 16.4 x > −11 , ou seja :
(1 + 4 − 16).4 x > −11 ⇒ -11.4 x > −11 e daí, 4 x < 1
Porém, 4 x < 1 ⇒ 4 x < 4 0.
Como a base (4) é maior que 1, obtemos :
4 x < 40 ⇒ x < 0
Portanto S = IR - (reais negativos)
FUNÇÃO LOGARÍTMICA
A função f:IR+IR definida por f(x)=logax, com a≠1 e a>0, é chamada função
logarítmica de base a. O domínio dessa função é o conjunto IR+ (reais positivos,
maiores que zero) e o contradomínio é IR (reais).
57

58. GRÁFICO CARTESIANO DA FUNÇÃO LOGARÍTMICA
Temos 2 casos a considerar:
 quando a>1;
 quando 0<a<1.
Acompanhe nos exemplos seguintes, a construção do gráfico em cada caso:
3) y=log2x (nesse caso, a=2, logo a>1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos
a tabela e o gráfico abaixo:
x 1/4 1/2 1 2 4
y -2 -1 0 1 2
4) y=log(1/2)x (nesse caso, a=1/2, logo 0<a<1)
Atribuindo alguns valores a x e calculando os correspondentes valores de y, obtemos
a tabela e o gráfico abaixo:
x 1/4 1/2 1 2 4
y 2 1 0 -1 -2
58

59. Nos dois exemplos, podemos observar que
d) o gráfico nunca intercepta o eixo vertical;
e) o gráfico corta o eixo horizontal no ponto (1,0). A raiz da função é x=1;
f) y assume todos os valores reais, portanto o conjunto imagem é Im=IR.
Além disso, podemos estabelecer o seguinte:
a>1 0<a<1
f(x) é crescente e Im=IR f(x) é decrescente e Im=IR
Para quaisquer x1 e x2 do domínio: Para quaisquer x1 e x2 do domínio:
x2>x1 ⇒ y2>y1 (as desigualdades têm x2>x1 ⇒ y2<y1 (as desigualdades têm
mesmo sentido) sentidos diferentes)
59

60. EQUAÇÕES LOGARÍTMICAS
Chamamos de equações logarítmicas toda equação que envolve logaritmos com
a incógnita aparecendo no logaritmando, na base ou em ambos.
Exemplos de equações logarítmicas:
7) log3x =5 (a solução é x=243)
2
8) log(x -1) = log 3 (as soluções são x’=-2 e x’’=2)
9) log2(x+3) + log2(x-3) = log27 (a solução é x=4)
2
10) logx+1(x -x)=2 (a solução é x=-1/3)
Alguns exemplos resolvidos:
1)log3(x+5) = 2
Resolução: condição de existência: x+5>0 => x>-5
log3(x+5) = 2 => x+5 = 32 => x=9-5 => x=4
Como x=4 satisfaz a condição de existência, então o conjunto solução é
S={4}.
2) log2(log4 x) = 1
Resolução: condição de existência: x>0 e log4x>0
log2(log4 x) = 1 ; sabemos que 1 = log2(2), então
log2(log4x) = log2(2) => log4x = 2 => 42 = x => x=16
Como x=16 satisfaz as condições de existência, então o conjunto solução
é S={16}.
3) Resolva o sistema:
log x + log y = 7

3. log x − 2. log y = 1
Resolução: condições de existência: x>0 e y>0
Da primeira equação temos:
log x+log y=7 => log y = 7-log x
Substituindo log y na segunda equação temos:
3.log x – 2.(7-log x)=1 => 3.log x-14+2.log x = 1 => 5.log x = 15 =>
=> log x =3 => x=103
Substituindo x= 103 em log y = 7-log x temos:
log y = 7- log 103 => log y = 7-3 => log y =4 => y=104.
Como essas raízes satisfazem as condições de existência, então o conjunto solução é
S={(103;104)}.
60

61. INEQUAÇÕES LOGARÍTMICAS
Chamamos de inequações logarítmicas toda inequação que envolve logaritmos
com a incógnita aparecendo no logaritmando, na base ou em ambos.
Exemplos de inequações logarítmicas:
1) log2x > 0 (a solução é x>1)
2) log4(x+3) ≤ 1 (a solução é –3<x≤1)
Para resolver inequações logarítmicas, devemos realizar dois passos importantes:
1º) redução dos dois membros da inequação a logaritmos de mesma base;
2º) aplicação da propriedade:
a>1 0<a<1
logam > logan ⇒ m>n>0 logam > logan ⇒ 0<m<n
(as desigualdades têm mesmo sentido) (as desigualdades têm sentidos
diferentes)
EXERCÍCIOS RESOLVIDOS:
1) log2(x+2) > log28
Resolução:
Condições de existência: x+2>0, ou seja, x>-2 (S1)
Como a base (2) é maior que 1, temos:
x+2>8 e, daí, x>6 (S2)
O conjunto solução é S= S1 ∩ S2 = {x ∈ IR| x>6}.
Portanto a solução final é a intersecção de S1 e S2, como está representado logo
abaixo no desenho:
2) log2(log3x) ≥ 0
Resolução:
Condições de existência: x>0 e log3x>0
Como log21=0, a inequação pode ser escrita assim:
log2(log3x) ≥ log21
Sendo a base (2) maior que 1, temos: log3x ≥ 1.
Como log33 = 1, então, log3x ≥ log33 e, daí, x ≥ 3, porque a base (3) é maior que 1.
As condições de existência estão satisfeitas, portanto S={x ∈ IR| x ≥ 3}.
61

62. FUNÇÃO MODULAR
• Módulo (ou valor absoluto) de um número
O módulo (ou valor absoluto) de um número real x, que se indica por | x | é definido da seguinte
maneira:
 x, se x ≥ 0
x =
− x, se x < 0
Então:
 se x é positivo ou zero, | x | é igual ao próprio x.
Exemplos: | 2 | = 2 ; | 1/2 | = | 1/2 | ; | 15 | = 15
 se x é negativo, | x | é igual a -x.
Exemplos: | -2 | = -(-2) = 2 ; | -20 | = -(-20) = 20
O módulo de um número real é sempre positivo ou nulo. O módulo de um número real nunca é
negativo.
Representando geometricamente, o módulo de um número real x é igual a distância do ponto que
representa, na reta real, o número x ao ponto 0 de origem. Assim:
• Se | x | < a (com a>0) significa que a distância entre x e a origem é menor que a, isto é, x deve
estar entre –a e a, ou seja, | x | < a ⇔ -a < x < a.
• Se | x | > a (com a>0) significa que a distância entre x e a origem é maior que a, isto é, deve
estar à direita de a ou à esquerda de –a na reta real, ou seja: | x | > a ⇔ x > a ou x < -a.
• Equações modulares
Toda a equação que contiver a incógnita em um módulo num dos membros será chamada equação
modular.
Exemplos:
a) | x2-5x | = 1
b) | x+8 | = | x2-3 |
62

63. ALGUMAS EQUAÇÕES MODULARES RESOLVIDAS:
1) Resolver a equação | x2-5x | = 6.
Resolução: Temos que analisar dois casos:
caso 1: x2-5x = 6
caso 2: x2-5x = -6
Resolvendo o caso 1:
x2-5x-6 = 0 => x’=6 e x’’=-1.
Resolvendo o caso 2:
x2-5x+6 = 0 => x’=3 e x’’=2.
Resposta: S={-1,2,3,6}
2) Resolver a equação | x-6 | = | 3-2x |.
Resolução: Temos que analisar dois casos:
caso 1: x-6 = 3-2x
caso 2: x-6 = -(3-2x)
Resolvendo o caso 1:
x-6 = 3-2x => x+2x = 3+6 => 3x=9 => x=3
Resolvendo o caso 2:
x-6 = -(3-2x) => x-2x = -3+6 => -x=3 => x=-3
Resposta: S={-3,3}
• Inequações modulares
Chamamos de inequações modulares as inequações nos quais aparecem módulos de expressões que
contém a incógnita.
Algumas inequações modulares resolvidas:
1) Resolver a inequação | -2x+6 | < 2.
Resolução:
 − 2 < −2 x + 6 2 x < 6 + 2
| - 2x + 6 | < 2 ⇒ − 2 < −2 x + 6 < 2 ⇒  ⇒  ⇒
− 2 x + 6 < 2 − 2 x < 4
2 x < 8 x < 4
⇒  ⇒ 
2 x > 4 x > 2
S = {x ∈ IR | 2<x<4}
63

64. 2) Dê o conjunto solução da inequação |x2-2x+3| ≤ 4.
Resolução:
|x2-2x+3| ≤ 4 => -4 ≤ x2-2x+3 ≤ 4.
Então temos duais inequações (que devem ser satisfeitas ao mesmo tempo):
Eq.1: -4 ≤ x2-2x+3
Eq.2: x2-2x+3 ≤ 4
Resolvendo a Eq.1:
-4 ≤ x2-2x+3 => -4-3 ≤ x2-2x => -7 ≤ x2-2x => x2-2x+7 ≥ 0 => sem raízes reais
Resolvendo a Eq.2:
x2-2x+3 ≤ 4 => x2-2x-1 ≤ 0
 x' = 1 − 2

Aplicando Bhaskara encontramos as raízes 
 x' ' = 1 + 2

S = {x ∈ IR | 1 − 2 ≤ x ≤ 1 + 2}
• Módulo e raiz quadrada
Consideremos os números reais x e y.
Temos por definição, que
x=y
se e somente se, y2 = x e y≥0. Daí podemos concluir que
x2 = x
só é verdadeiro se x≥0.
Se tivermos x<0, não podemos afirmar que
x2 = x
pois isso contradiz a definição.
Por exemplo, se x=-3, teríamos:
( −3) 2 = −3
o que é um absurdo, pois o primeiro membro é positivo e o segundo negativo. Usando a definição
de módulo, podemos escrever:
x 2 =| x |
o que é verdadeiro para todo x real.
Devemos proceder da mesma forma em relação a todas raízes de índice par:
4
x 4 =| x |, 6
x 6 =| x |, 2n
x 2 n =| x |, com x ∈ IR e n ∈ IN *
Com relação às raízes de índice ímpar, podemos escrever:
2 n +1
3
x 3 = x, 5
x 5 = x, x 2 n+1 = x, com x ∈ IR e n ∈ IN
64

65. • Função modular
Chamamos de função modular a função f(x)=|x| definida por:
 x, se x ≥ 0
f ( x) = 
− x, se x < 0
Observe, então, que a função modular é uma função definida por duas sentenças.
 Determinação do domínio
Vamos determinar o domínio de algumas funções utilizando inequações modulares:
Exemplo 1: Determinar o domínio da função
1
f ( x) =
| x | −3
Resolução:
1
Sabemos que só é possível em IR se | x | −3 ≠ 0.
| x | −3
Então : | x | −3 ≠ 0 ⇒ | x |≠ 3 ⇒ x ≠ 3 ou x ≠ −3
Resposta : D = {x ∈ IR | x ≠ 3 ou x ≠ −3}
Exemplo 2: Determinar o domínio da função
f ( x ) = 2− | x − 1 |
Resolução:
Sabemos que 2− | x − 1 | só é possível em IR se 2− | x − 1 |≥ 0.
Então : 2− | x − 1 |≥ 0 ⇒ − | x − 1 |≥ −2 ⇒ | x − 1 |≤ 2 ⇒ − 2 ≤ x − 1 ≤ 2
− 2 ≤ x −1 ≤ 2 ⇒ − 2 +1 ≤ x ≤ 2 +1 ⇒ −1 ≤ x ≤ 3
Resposta : D = {x ∈ IR | −1 ≤ x ≤ 3}
 Gráfico
Vamos construir o gráfico da função f(x)=|x|:
x y=f(x)
-1 1
-2 2
0 0
1 1
2 2
65

66. CONJUNTOS NUMÉRICOS
• Conjunto dos números naturais (IN)
IN={0, 1, 2, 3, 4, 5,...}
Um subconjunto importante de IN é o conjunto IN*:
IN*={1, 2, 3, 4, 5,...}  o zero foi excluído do conjunto IN.
Podemos considerar o conjunto dos números naturais ordenados sobre uma reta,
como mostra o gráfico abaixo:
• Conjunto dos números inteiros (Z)
Z={..., -3, -2, -1, 0, 1, 2, 3,...}
O conjunto IN é subconjunto de Z.
Temos também outros subconjuntos de Z:
Z* = Z-{0}
Z+ = conjunto dos inteiros não negativos = {0,1,2,3,4,5,...}
Z_ = conjunto dos inteiros não positivos = {0,-1,-2,-3,-4,-5,...}
Observe que Z+=IN.
Podemos considerar os números inteiros ordenados sobre uma reta, conforme mostra
o gráfico abaixo:
66

67. • Conjunto dos números racionais (Q)
Os números racionais são todos aqueles que podem ser colocados na forma de
fração (com o numerador e denominador ∈ Z). Ou seja, o conjunto dos números
racionais é a união do conjunto dos números inteiros com as frações positivas e
negativas.
5 3 3
Então : -2, − , − 1, , 1, , por exemplo, são números racionais.
4 5 2
Exemplos:
−3 −6 −9
a) − 3 = = =
1 2 3
1 2 3
b) 1 = = =
1 2 3
Assim, podemos escrever:
a
Q = {x | x = , com a ∈ Z , b ∈ Z e b ≠ 0}
b
É interessante considerar a representação decimal de um número racional , que se
obtém a dividindo a por b.
b
Exemplos referentes às decimais exatas ou finitas:
1 5 75
= 0,5 − = −1,25 = 3,75
2 4 20
Exemplos referentes às decimais periódicas ou infinitas:
1 6 7
= 0,333... = 0,857142857142... = 1,1666...
3 7 6
Toda decimal exata ou periódica pode ser representada na forma de número
racional.
67

68. • Conjunto dos números irracionais
Os números irracionais são decimais infinitas não periódicas, ou seja, os números
que não podem ser escrito na forma de fração (divisão de dois inteiros). Como exemplo
de números irracionais, temos a raiz quadrada de 2 e a raiz quadrada de 3:
2 = 1,4142135...
3 = 1,7320508...
Um número irracional bastante conhecido é o número π=3,1415926535...
• Conjunto dos números reais (IR)
Dados os conjuntos dos números racionais (Q) e dos irracionais, definimos o
conjunto dos números reais como:
IR=Q ∪ {irracionais} = {x|x é racional ou x é irracional}
O diagrama abaixo mostra a relação entre os conjuntos numéricos:
Portanto, os números naturais, inteiros, racionais e irracionais são todos
números reais. Como subconjuntos importantes de IR temos:
IR* = IR-{0}
IR+ = conjunto dos números reais não negativos
IR_ = conjunto dos números reais não positivos
Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:
• Entre os números 1 e 2 existem infinitos números reais:
1,01 ; 1,001 ; 1,0001 ; 1,1 ; 1,2 ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...
• Entre os números 5 e 6 existem infinitos números reais:
5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...
68

69. Binômio de Newton
Introdução
Pelos produtos notáveis, sabemos que (a+b)² = a² + 2ab + b².
Se quisermos calcular (a + b)³, podemos escrever:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Se quisermos calcular , podemos adotar o mesmo procedimento:
(a + b)4 = (a + b)3 (a+b) = (a3 + 3a2b + 3ab2 + b3) (a+b)
= a4 + 4a3b + 6a2b2 + 4ab3 + b4
De modo análogo, podemos calcular as quintas e sextas potências e, de modo geral, obter o
desenvolvimento da potência a partir da anterior, ou seja, de .
Porém quando o valor de n é grande, este processo gradativo de cálculo é muito trabalhoso.
Existe um método para desenvolver a enésima potência de um binômio, conhecido como binômio de
Newton (Isaac Newton, matemático e físico inglês, 1642 - 1727). Para esse método é necessário saber o que
são coeficientes binomiais, algumas de suas propriedades e o triângulo de Pascal.
Coeficientes Binomiais
Sendo n e p dois números naturais , chamamos de coeficiente binomial de classe p, do número n,
o número , que indicamos por (lê-se: n sobre p). Podemos escrever:
O coeficiente binomial também é chamado de número binomial. Por analogia com as frações, dizemos que
n é o seu numerador e p, o denominador. Podemos escrever:
É também imediato que, para qualquer n natural, temos:
Exemplos:
69

70. Propriedades dos coeficientes binomiais
1ª)
Se n, p, k e p + k = n então
Coeficientes binomiais como esses, que tem o mesmo numerador e a soma dos denominadores igual ao
numerador, são chamados complementares.
Exemplos:
Se n, p, k ep p-1 0 então
2ª)
Essa igualdade é conhecida como relação de Stifel (Michael Stifel, matemático alemão, 1487 - 1567).
Exemplos:
Triângulo de Pascal
A disposição ordenada dos
números binomiais, como na
tabela ao lado, recebe o nome
de Triângulo de Pascal
Nesta tabela triangular, os números binomiais com o mesmo numerador são escritos na mesma linha e os
de mesmo denominador, na mesma coluna.
70

71. Por exemplo, os números binomiais , , e estão na linha 3 e os números binomiais , , ,
, ..., , ... estão na coluna 1.
Substituindo cada número binomial pelo seu respectivo valor, temos:
Construção do triângulo de Pascal
Para construir o triângulo do Pascal, basta lembrar as seguintes propriedades dos números binomiais, não
sendo necessário calculá-los:
1ª) Como = 1, todos os elementos da coluna 0 são iguais a 1.
2ª) Como = 1, o último elemento de cada linha é igual a 1.
3ª) Cada elemento do triângulo que não seja da coluna 0 nem o último de cada linha é igual à soma daquele
que está na mesma coluna e linha anterior com o elemento que se situa à esquerda deste último (relação
de Stifel).
Observe os passos e aplicação da relação de Stifel para a construção do triângulo:
Propriedade do triângulo de Pascal
P1 Em Qualquer linha, dois números binomiais eqüidistantes dos extremos são iguais.
71

72. De fato, esses binomiais são complementares.
P2 Teorema das linhas: A soma dos elementos da enésima linha é .
De modo geral temos:
P3 Teorema das colunas: A soma dos elementos de qualquer coluna, do 1º elemento até um qualquer, é
igual ao elemento situado na coluna à direita da considerada e na linha imediatamente abaixo.
1 + 2 + 3 + 4 + 5 + 6 = 21
1 + 4 + 10 + 20 = 35
P4 Teorema das diagonais: A soma dos elementos situados na mesma diagonal desde o elemento da 1ª
coluna até o de uma qualquer é igual ao elemento imediatamente abaixo deste.
72

73. 1 + 3 + 6 + 10 + 15 = 35
Fórmula do desenvolvimento do binômio de Newton
Como vimos, a potência da forma , em que a, , é chamada binômio de Newton.
Além disso:
• quando n = 0 temos
• quando n = 1 temos
• quando n = 2 temos
• quando n = 3 temos
• quando n = 4 temos
Observe que os coeficientes dos desenvolvimentos foram o triângulo de Pascal. Então, podemos escrever
também:
73

74. De modo geral, quando o expoente é n, podemos escrever a fórmula do desenvolvimento do binômio de
Newton:
Note que os expoentes de a vão diminuindo de unidade em unidade, variando de n até 0, e os expoentes de
b vão aumentando de unidade em unidade, variando de 0 até n. O desenvolvimento de (a + b)n possui n + 1
termos.
Fórmula do termo geral do binômio
Observando os termos do desenvolvimento de (a + b)n, notamos que cada um deles é da
forma .
• Quando p = 0 temos o 1º termo:
• Quando p = 1 temos o 2º termo:
• Quando p = 2 temos o 3º termo:
• Quando p = 3 temos o 4º termo:
• Quando p = 4 temos o 5º termo:
..............................................................................
Percebemos, então, que um termo qualquer T de ordem p + 1pode ser expresso por:
74

75. Sistemas Lineares
Equação linear
Equação linear é toda equação da forma:
a1x1 + a2x2+ a3x3 + ... + anxn = b
em que a1, a2, a3, ... , an são números reais, que recebem o nome de coeficientes das incógnitas
x1, x2,x3, ... , xn, e b é um número real chamado termo independente ( quando b=0, a equação recebe o nome
de linear homogênea).
Veja alguns exemplos de equações lineares:
• 3x - 2y + 4z = 7 • -2x + 4z = 3t - y + 4
• (homogênea)
As equações a seguir não são lineares:
• xy - 3z + t = 8 • x2- 4y = 3t - 4 •
Sistema linear
Um conjunto de equações lineares da forma:
é um sistema linear de m equações e n incógnitas.
A solução de um sistema linear é a n-upla de números reais ordenados (r1, r2, r3,..., rn) que é,
simultaneamente, solução de todas as equações do sistema.
Sistemas Lineares
Matrizes associadas a um sistema linear
75

76. A um sistema linear podemos associar as seguintes matrizes:
• matriz incompleta: a matriz A formada pelos coeficientes das incógnitas do sistema.
Em relação ao sistema:
a matriz incompleta é:
• matriz completa: matriz B que se obtém acrescentando à matriz incompleta uma última coluna formada
pelos termos independentes das equações do sitema.
Assim, para o mesmo sistema acima, a matriz completa é:
Sistemas homogêneos
Um sistema é homogêneo quando todos os termos independentes da equações são nulos:
Veja um exemplo:
A n-upla (0, 0, 0,...,0) é sempre solução de um sistema homogêneo com n incógnitas e recebe o nome de
solução trivial. Quando existem, as demais soluções são chamadas não-triviais.
Classificação de um sistema quanto ao número de soluções
76

77. Resolvendo o sistema , encontramos uma única solução: o par ordenado (3,5). Assim, dizemos
que o sistema é possível (tem solução) e determinado (solução única).
No caso do sistema , verificamos que os pares ordenados (0,8), (1,7),(2,6),(3,5),(4,4),(5,3),...são
algumas de suas infinitas soluções. Por isso, dizemos que o sistema é possível (tem solução) e indeterminado
(infinitas soluções).
Para , verificamos que nenhum par ordenado satisfaz simultaneamente as equações. Portanto, o
sistema é impossível (não tem solução).
Resumindo, um sistema linear pode ser:
a) possível e determinado (solução única);
b) possível e indeterminado (infinitas soluções);
c) impossível (não tem solução).
Sistema normal
Um sistema é normal quando tem o mesmo número de equações (m) e de incógnitas (n) e o determinante da
matriz incompleta associada ao sistema é diferente de zero.
Se m=n e det A 0, então o sistema é normal.
Regra de Cramer
Todo sistema normal tem uma única solução dada por:
em que i { 1,2,3,...,n}, D= det A é o determinante da matriz incompleta associada ao sistema, e Dxi é o
determinante obtido pela substituição, na matriz incompleta, da coluna i pela coluna formada pelos termos
independentes.
Discussão de um sistema linear
77

78. Se um sistema linear tem n equações e n incógnitas, ele pode ser:
a) possível e determinado, se D=det A 0; caso em que a solução é única.
Exemplo:
m=n=3
Então, o sistema é possível e determinado, tendo solução única.
b) possível e indeterminado, se D= Dx1 = Dx2 = Dx3 = ... = Dxn= 0, para n=2. Se n 3, essa condição só será
válida se não houver equações com coeficientes das incógnitas respectivamente proporcionais e termos
independentes não-proporcionais.
Um sistema possível e indeterminado apresenta infinitas soluções.
Exemplo:
D=0, Dx =0, Dy=0 e Dz=0
Assim, o sistema é possível e indeterminado, tendo infinitas soluções.
c) impossível, se D=0 e Dxi 0, 1 i n; caso em que o sistema não tem solução.
Exemplo:
Como D=0 e Dx 0, o sistema é impossível e não apresenta solução.
Sistemas Equivalentes
78

79. Dois sistemas são equivalentes quando possuem o mesmo conjunto solução.
Por exemplo, dados os sistemas:
e
verificamos que o par ordenado (x, y) = (1, 2) satisfaz ambos e é único. Logo, S1 e S2 são equivalentes: S1 ~ S2.
Propriedades
a) Trocando de posição as equações de um sistema, obtemos outro sistema equivalente.
Por exemplo:
e
S1 ~S2
b) Multiplicando uma ou mais equações de um sistema por um número K (K IR*), obtemos um sistema
equivalente ao anterior. Por exemplo:
S1 ~S2
c) Adicionando a uma das equações de um sistema o produto de outra equação desse mesmo sistema por um
número k ( K IR*), obtemos um sistema equivalente ao anterior.
Por exemplo:
Dado , substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos:
S1~S2, pois (x,y)=(2,1) é solução de ambos os sistemas.
Sistemas escalonados
79

80. Utilizamos a regra de Cramer para discutir e resolver sistemas lineares em que o número de equações (m) é
igual ao número de incógnitas (n). Quando m e n são maiores que três, torna-se muito trabalhoso utilizar essa
regra. Por isso, usamos a técnica do escalonamento, que facilita a discussão e resolução de quaisquer
sistemas lineares.
Dizemos que um sistema, em que existe pelo menos um coeficiente não-nulo em cada equação, está
escalonado se o número de coeficientes nulos antes do primeiro coeficiente não nulo aumenta de equação
para equação.
Para escalonar um sistema adotamos o seguinte procedimento:
a) Fixamos como 1º equação uma das que possuem o coeficiente da 1º incógnita diferente de zero.
b) Utilizando as propriedades de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das
demais equações.
c) Repetimos o processo com as demais incógnitas, até que o sistema se torne escalonado.
Vamos então aplicar a técnica do escalonamento, considerando dois tipos de sistema:
I. O número de equações é igual ao número de incógnitas (m=n)
Exemplo 1:
1ºpasso: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação, aplicando as propriedades
dos sistemas equivalentes:
• Trocamos de posição a 1º equação com a 2º equação, de modo que o 1º coeficiente de x seja igual a
1:
• Trocamos a 2º equação pela soma da 1º equação, multiplicada por -2, com a 2º equação:
• Trocamos a 3º equação pela soma da 1º equação, multiplicada por -3, com a 3º equação:
80

81. 2º passo: Anulamos os coeficientes da 2º incógnita a partir da 3º equação:
• Trocamos a 3º equação pela soma da 2º equação, multiplicada por -1, com a 3º equação:
Agora o sistema está escalonado e podemos resolvê-lo.
-2z=-6 z=3
Substituindo z=3 em (II):
-7y - 3(3)= -2 -7y - 9 = -2 y=-1
Substituindo z=3 e y=-1 em (I):
x + 2(-1) + 3= 3 x=2
Então, x=2, y=-1 e z=3
Exemplo 2:
1º passo: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação:
• Trocamos a 2º equação pela soma do produto da 1º equação por -2 com a 2º equação:
• Trocamos a 3º equação pela soma do produto da 1º equação por -3 com a 3º equação:
2º passo: Anulamos os coeficientes da 2ª incógnita, a partir da 3º equação:
• Trocamos a 3ª equação pela soma do produto da 2ª equação por -1 com a 3º equação:
Dessa forma, o sistema está escalonando. Como não existe valor real de z tal que 0z=-2, o sistema é
impossível.
81

82. II) O número de equações é menor que o número de incógnitas (m < n)
Exemplo:
1º passo: Anulamos todos os coeficientes da 1º incógnita a partir da 2º equação:
• Trocamos a 2º equação pela soma do produto da 1º equação por -2 com a 2º equação:
• Trocamos a 3º equação pela soma do produto da 1º equação por -1 com a 3º equação:
2º passo: Anulamos os coeficientes da 2º incógnita, a partir da 3º equação:
• Trocamos a 3º equação pela soma do produto da 2º equação por -3 com a 3º equação
O sistema está escalonado. Como m<n, o sistema é possível e indeterminado, admitindo infinitas soluções. A
diferença entre o número de incógnitas (n) e o de equações (m) de um sistema nessas condições é chamada
grau de indeterminação (GI):
GI= n - m
Para resolver um sistema indeterminado, procedemos do seguinte modo:
• Consideramos o sistema em sua forma escalonada:
• Calculamos o grau de indeterminação do sistema nessas condições:
GI = n-m = 4-3 = 1
Como o grau de indeterminação é 1, atribuímos a uma das incógnitas um valor , supostamente conhecido, e
resolvemos o sistema em função desse valor. Sendo t= , substituindo esse valor na 3º equação, obtemos:
12z - 6 = 30 12z= 30 + 6 =
82

83. Conhecidos z e t, substituímos esses valores na 2º equação:
Conhecidos z,t e y, substituímos esses valores na 1º equação:
Assim, a solução do sistema é dada por S= , com IR.
Para cada valor que seja atribuído a , encontraremos uma quádrupla que é solução para o sistema.
Inequações Trigonométricas
INTRODUÇÃO
Quando encontramos função trigonométrica da incógnita ou função trigonométrica de alguma
função da incógnita em pelo menos um dos membros de uma inequação, dizemos que esta inequação é
trigonométrica.
Exemplos:
1) sen x > e sen2 x + tg 2 são inequações trigonométricas.
2) ( sen 30º) . (x2 - 1) > 0 não são inequações trigonométricas.
Resolver uma inequação como f(x) < g(x), por exemplo, significa determinar o conjunto S dos
números s, sendo s elemento do domínio de f e de g, tais que f(s) < g(s).
O conjunto S é chamado de conjunto solução da inequação e todo elemento de S é uma solução
da inequação.
Assim, na inequação sen x > , os números são algumas de suas soluções e os números
não o são.
83

84. RESOLUÇÃO DAS INEQUAÇÕES TRIGONOMÉTRICAS FUNDAMENTAIS
Quase todas as inequações trigonométricas, quando convenientemente tratadas e transformadas,
podem ser reduzidas a pelo menos uma das inequações fundamentais. Vamos conhecê-las, a seguir, através
de exemplos.
1º caso : sen x < sen a (sen x sen a)
Por exemplo, ao resolvermos a inequação
encontramos, inicialmente,
, que é uma solução particular no intervalo . Acrescentando às
extremidades dos intervalos encontrados, temos a solução geral em IR, que é:
O conjunto solução é, portanto:
Por outro lado, se a inequação fosse , então, bastaria incluir as extremidades de
e o conjunto solução seria:
84

85. 2º caso: sen x > sen a (sen x sen a)
Por exemplo, ao resolvermos a inequação sen x > sen ou sen x > encontramos, inicialmente,
, que é uma uma solução
particular no intervalo .
Acrescentando às extremidades dos intervalos encontrados, temos a solução geral em IR, que é:
O conjunto solução é , portanto:
3º caso: cos x < cos a (cos x cos a)
85

86. Por exemplo, ao resolvermos a inequação
encontramos, inicialmente,
, que é uma solução particular no intervalo
.
Acrescentando às extremidades do intervalo encontrado, temos a solução geral em IR,
que é:
O conjunto solução é, portanto:
Por outro lado, se a inequação fosse cos x cos ou cos x , então, bastaria incluir as extremidades de
e o conjunto solução seria:
4º caso: cos x > cos a ( cos x cos a)
86

87. Por exemplo, ao resolvermos a inequação encontramos, inicialmente,
, que é uma solução particular no intervalo . Acrescentando )
às extremidades
dos intervalos encontrados, temos o conjunto solução seguinte:
5º caso: tg x < tg a (tg x tg a)
Por exemplo, ao resolvermos a inequação encontramos, inicialmente,
, que é uma solução particular no intervalo .
A solução geral em IR pode ser expressa por .
O conjunto solução é, portanto:
87

88. 6º caso: tg x > tg a ( tg x tg a)
Vamos estudar este último caso resolvendo a inequação tg x > tg como exemplo.
Então, na resolução da inequação encontramos, inicialmente,
, que é uma solução particular no intervalo .
A solução geral em IR pode ser expressa por
.
O conjunto solução é, portanto:
88

89. Matrizes
Introdução
O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em
áreas como Economia, Engenharia, Matemática, Física, dentre outras. Vejamos um exemplo.
A tabela a seguir representa as notas de três alunos em uma etapa:
Química Inglês Literatura Espanhol
A 8 7 9 8
B 6 6 7 6
C 4 8 5 9
Se quisermos saber a nota do aluno B em Literatura, basta procurar o número que fica na segunda linha e na
terceira coluna da tabela.
Vamos agora considerar uma tabela de números dispostos em linhas e colunas, como no exemplo acima,
mas colocados entre parênteses ou colchetes:
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e
as colunas, da esquerda para direita:
Tabelas com m linhas e n colunas ( m e n números naturais diferentes de 0) são denominadas matrizes m x
n. Na tabela anterior temos, portanto, uma matriz 3 x 3.
Veja mais alguns exemplos:
• é uma matriz do tipo 2 x 3
• é uma matriz do tipo 2 x 2
89

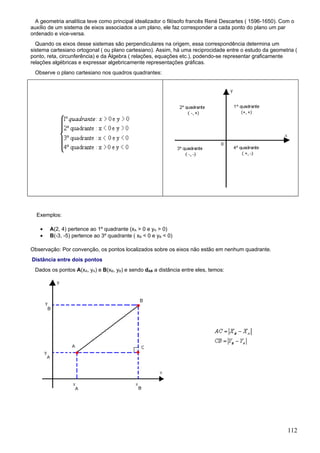
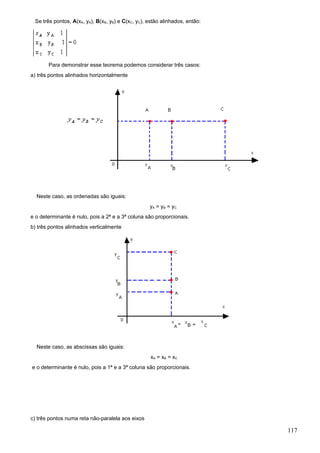
90. Notação geral
Costuma-se representar as matrizes por letras maiúsculas e seus elementos por letras minúsculas,
acompanhadas por dois índices que indicam, respectivamente, a linha e a coluna que o elemento ocupa.
Assim, uma matriz A do tipo m x n é representada por:
ou, abreviadamente, A = [aij]m x n, em que i e j representam, respectivamente, a linha e a coluna que o elemento
ocupa. Por exemplo, na matriz anterior, a23 é o elemento da 2ª linha e da 3ª coluna.
Na matriz , temos:
Ou na matriz B = [ -1 0 2 5 ], temos: a11 = -1, a12 = 0, a13 = 2 e a14 = 5.
Denominações especiais
Algumas matrizes, por suas características, recebem denominações especiais.
• Matriz linha: matriz do tipo 1 x n, ou seja, com uma única linha. Por exemplo, a matriz A =[4 7 -3 1], do
tipo 1 x 4.
• Matriz coluna: matriz do tipo m x 1, ou seja, com uma única coluna. Por exemplo, , do tipo 3 x
1
• Matriz quadrada: matriz do tipo n x n, ou seja, com o mesmo número de linhas e colunas; dizemos
que a matriz é de ordem n. Por exemplo, a matriz é do tipo 2 x 2, isto é, quadrada de
ordem 2.
90

91. Numa matriz quadrada definimos a diagonal principal e a diagonal secundária. A principal é formada pelos
elementos aij tais que i = j. Na secundária, temos i + j = n + 1. Veja:
Observe a matriz a seguir:
a11 = -1 é elemento da diagonal principal, pis i = j = 1
a31= 5 é elemento da diagonal secundária, pois i + j = n + 1 ( 3 + 1 = 3 + 1)
• Matriz nula: matriz em que todos os elementos são nulos; é representada por 0m x n.
Por exemplo, .
• Matriz diagonal: matriz quadrada em que todos os elementos que não estão na diagonal principal são
nulos. Por exemplo:
• Matriz identidade: matriz quadrada em que todos os elementos da diagonal principal são iguais a 1 e
os demais são nulos; é representada por In, sendo n a ordem da matriz. Por exemplo:
Assim, para uma matriz identidade .
91

92. • Matriz transposta: matriz At obtida a partir da matriz A trocando-se ordenadamente as linhas por
colunas ou as colunas por linhas. Por exemplo:
Desse modo, se a matriz A é do tipo m x n, At é do tipo n x m.
Note que a 1ª linha de A corresponde à 1ª coluna de At e a 2ª linha de A corresponde à 2ª coluna de At.
• Matriz simétrica: matriz quadrada de ordem n tal que A = At . Por exemplo,
é simétrica, pois a12 = a21 = 5, a13 = a31 = 6, a23 = a32 = 4, ou seja, temos sempre a ij
= a ij.
• Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por
exemplo, .
Igualdade de matrizes
Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a
mesma posição são iguais:
.
92

93. Operações envolvendo matrizes
Adição
Dadas as matrizes , chamamos de soma dessas matrizes a matriz ,
tal que Cij = aij + bij , para todo :
A+B=C
Exemplos:
•
•
Observação: A + B existe se, e somente se, A e B forem do mesmo tipo.
Propriedades
Sendo A, B e C matrizes do mesmo tipo ( m x n), temos as seguintes propriedades para a adição:
a) comutativa: A + B = B + A
b) associativa: ( A + B) + C = A + ( B + C)
c) elemento neutro: A + 0 = 0 + A = A, sendo 0 a matriz nula m x n
d) elemento oposto: A + ( - A) = (-A) + A = 0
Subtração
Dadas as matrizes , chamamos de diferença entre essas matrizes a soma de A
com a matriz oposta de B:
A-B=A+(-B)
Observe:
Multiplicação de um número real por uma matriz
Dados um número real x e uma matriz A do tipo m x n, o produto de x por A é uma matriz B do tipo m x n
obtida pela multiplicação de cada elemento de A por x, ou seja, bij = xaij:
B = x.A
Observe o seguinte exemplo:
93

94. Propriedades
Sendo A e B matrizes do mesmo tipo ( m x n) e x e y números reais quaisquer, valem as seguintes
propriedades:
a) associativa: x . (yA) = (xy) . A
b) distributiva de um número real em relação à adição de matrizes: x . (A + B) = xA + xB
c) distributiva de uma matriz em relação à adição de dois números reais: (x + y) . A = xA + yA
d) elemento neutro : xA = A, para x=1, ou seja, A=A
Multiplicação de matrizes
O produto de uma matriz por outra não é determinado por meio do produto dos sus respectivos elementos.
Assim, o produto das matrizes A = ( aij) m x p e B = ( bij) p x n é a matriz C = (cij) m x n em que cada elemento cij é
obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos
da j-ésima coluna B.
Vamos multiplicar a matriz para entender como se obtém cada Cij:
• 1ª linha e 1ª coluna
• 1ª linha e 2ª coluna
• 2ª linha e 1ª coluna
• 2ª linha e 2ª coluna
94

95. Assim, .
Observe que:
Portanto, .A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
Vejamos outro exemplo com as matrizes :
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número
de linhas de B:
A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):
• Se A3 x 2 e B 2 x 5 , então ( A . B ) 3 x 5
• Se A 4 x 1 e B 2 x 3, então não existe o produto
• Se A 4 x 2 e B 2 x 1, então ( A . B ) 4 x 1
Propriedades
Verificadas as condições de existência para a multiplicação de matrizes, valem as seguintes propriedades:
a) associativa: ( A . B) . C = A . ( B . C )
b) distributiva em relação à adição: A . ( B + C ) = A . B + A . C ou ( A + B ) . C = A . C + B . C
c) elemento neutro: A . In = In . A = A, sendo In a matriz identidade de ordem n
Vimos que a propriedade comutativa, geralmente, não vale para a multiplicação de matrizes. Não vale
também o anulamento do produto, ou seja: sendo 0 m x n uma matriz nula, A .B =0 m x n não implica,
necessariamente, que A = 0 m x n ou B = 0 m x n.
95

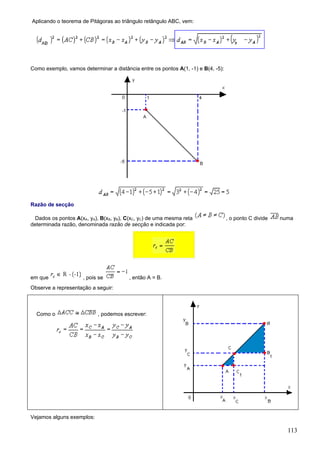
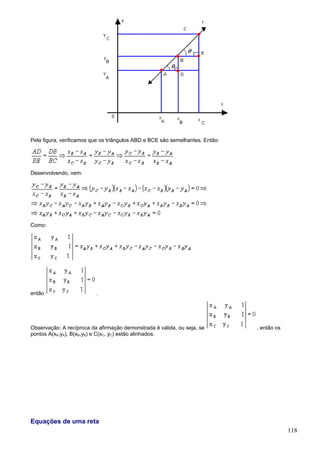
96. Matriz inversa
Dada uma matriz A, quadrada, de ordem n, se existir uma matriz A', de mesma ordem, tal que A . A' = A' . A
= In , então A' é matriz inversa de A . representamos a matriz inversa por A-1 .
Determinantes
Como já vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou seja, é do tipo
nxn).
A toda matriz quadrada está associado um número ao qual damos o nome de determinante.
Dentre as várias aplicações dos determinantes na Matemática, temos:
• resolução de alguns tipos de sistemas de equações lineares;
• cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas
dos seus vértices;
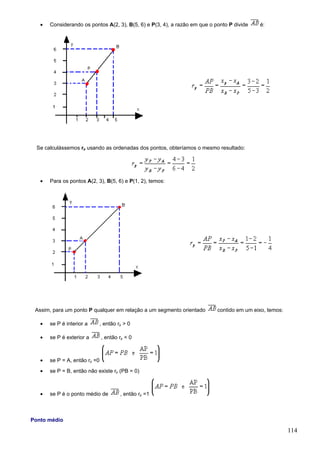
Determinante de 1ª ordem
Dada uma matriz quadrada de 1ª ordem M=[a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: Representamos o determinante de uma matriz entre duas barras verticais, que não têm o
significado de módulo.
Por exemplo:
• M= [5] det M = 5 ou I 5 I = 5 • M = [-3] det M = -3 ou I -3 I = -3
Determinante de 2ª ordem
Dada a matriz , de ordem 2, por definição o determinante associado a M, determinante de 2ª
ordem, é dado por:
Portanto, o determinante de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos da
diagonal principal e o produto dos elementos da diagonal secundária. Veja o exemplo a seguir.
96

97. Menor complementar
Chamamos de menor complementar relativo a um elemento aij de uma matriz M, quadrada e de ordem n>1, o
determinante MCij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que
passam por aij .
Vejamos como determiná-lo pelos exemplos a seguir:
a) Dada a matriz , de ordem 2, para determinar o menor complementar relativo ao elemento
a11(MC11), retiramos a linha 1 e a coluna 1:
Da mesma forma, o menor complementar relativo ao elemento a12 é:
b) Sendo , de ordem 3, temos:
• •
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de
ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada , os cofatores relativos aos elementos a11 e a12 da matriz M são:
b) Sendo , vamos calcular os cofatores A22, A23 e A31:
97

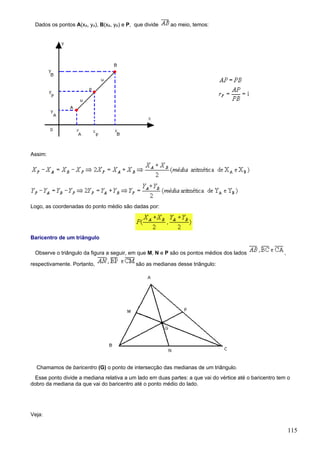
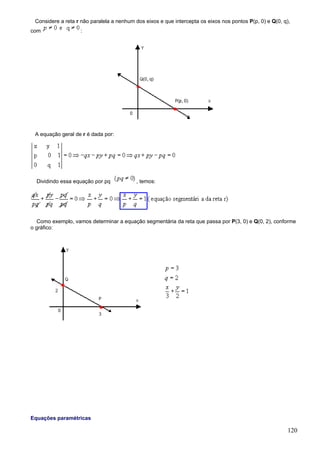
98. Teorema de Laplace
O determinante de uma matriz quadrada M = [aij]mxn pode ser obtido pela soma dos produtos dos
elementos de uma fila qualquer ( linha ou coluna) da matriz M pelos respectivos cofatores.
Assim, fixando , temos:
em que é o somatório de todos os termos de índice i, variando de 1 até m, .
Regra de Sarrus
O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra
de Sarrus.
98

99. Acompanhe como aplicamos essa regra para .
1º passo: Repetimos as duas primeiras colunas ao lado da terceira:
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos
pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos
obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a soma deve ser precedida do sinal
negativo):
Assim:
Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace,
encontraremos o mesmo número real.
Determinante de ordem n > 3
99

100. Vimos que a regra de Sarrus é válida para o cálculo do determinante de uma matriz de ordem 3. Quando a
matriz é de ordem superior a 3, devemos empregar o Teorema de Laplace para chegar a determinantes de
ordem 3 e depois aplicar a regra de Sarrus.
Propriedades dos determinantes
Os demais associados a matrizes quadradas de ordem n apresentam as seguintes propriedades:
P1 ) Quando todos os elementos de uma fila ( linha ou coluna) são nulos, o determinante dessa matriz é nulo.
Exemplo:
P2) Se duas filas de uma matriz são iguais, então seu determinante é nulo.
Exemplo:
P3) Se duas filas paralelas de uma matriz são proporcionais, então seu determinante é nulo.
Exemplo:
P4) Se os elementos de uma fila de uma matriz são combinações lineares dos elementos correspondentes de
filas paralelas, então seu determinante é nulo.
Exemplos:
P5 ) Teorema de Jacobi: o determinante de uma matriz não se altera quando somamos aos elementos de uma
fila uma combinação linear dos elementos correspondentes de filas paralelas.
100

101. Exemplo:
Substituindo a 1ª coluna pela soma dessa mesma coluna com o dobro da 2ª, temos:
P6) O determinante de uma matriz e o de sua transposta são iguais.
Exemplo:
P7) Multiplicando por um número real todos os elementos de uma fila em uma matriz, o determinante dessa
matriz fica multiplicado por esse número.
Exemplos:
P8) Quando trocamos as posições de duas filas paralelas, o determinante de uma matriz muda de sinal.
Exemplo:
101

102. P9) Quando, em uma matriz, os elementos acima ou abaixo da diagonal principal são todos nulos, o
determinante é igual ao produto dos elementos dessa diagonal.
Exemplos:
P10) Quando, em uma matriz, os elementos acima ou abaixo da diagonal secundária são todos nulos, o
determinante é igual ao produto dos elementos dessa diagonal multiplicado por .
Exemplos:
P11) Para A e B matrizes quadradas de mesma ordem n, . Como:
Exemplo:
P12)
102

103. Exemplo:
Geometria Espacial
103

104. Prismas: (triangular, quadrangular e hexagonal)
Obs: a letra "lambda" representa a medida do lado da base.
Paralelepípedo:
Cubo:
Pirâmide:
Tetraedro:
104

105. Cilindro:
Cone:
Esfera:
Esfera:
Tronco de Cone:
105

106. Fórmulas de Geometria Espacial
Prismas
2 3
AB∆ = AL∆ = 3. h
4
ABQ = 2 ALQ = 4. h
2 3
ABH = 6. ALH = 6. h
4
AT = AL + 2. AB V = AB . h
Paralelepípedo Cubo
AB = a. b AF =  2
AT = 2ab + 2bc + 2ac AL = 4 2
V = a. b. c AT = 6 2
D = a 2 + b2 + c2 V = 3
d face =  2 Dcubo =  3
106

107. Pirâmides
AL = p. ap ap 2 = h 2 + K 2
FI
+G
HJ
2
2K

AT = AL + AB a = ap
2 2
AB . h
V= a 2 = h2 + R 2
3
Tetraedro
a2 3 a3 2
AF = V=
4 12
a2 3
AT = a 2 3 AL = 3.
4
a 6
h= Obs: K = h do
3
triângulo equilátero
Cilindro
V = AB . h = πr 2 h AB = πr 2
AL = 2πrh
AT = 2πr 2 + 2πrh
AS = 2rh
Equilátero → h = 2r
107

108. Cone
AB . h πr 2 h
V= = AB = πr 2
3 3
AL = πrg AS = rh
AT = πr 2 + πrg g 2 = r 2 + h2
Equilátero → g = 2r
108

109. Geometria Analítica: Circunferência
Equações da circunferência
Equação reduzida
Circunferência é o conjunto de todos os pontos de um plano eqüidistantes de um ponto fixo, desse mesmo
plano, denominado centro da circunferência:
Assim, sendo C(a, b) o centro e P(x, y) um ponto qualquer da circunferência, a distância de C a P(dCP) é o
raio dessa circunferência. Então:
Portanto, (x - a)2 + (y - b)2 =r2 é a equação reduzida da circunferência e permite determinar os elementos
essenciais para a construção da circunferência: as coordenadas do centro e o raio.
Observação: Quando o centro da circunfer6encia estiver na origem ( C(0,0)), a equação da circunferência será
x2 + y2 = r2 .
Equação geral
Desenvolvendo a equação reduzida, obtemos a equação geral da circunferência:
Como exemplo, vamos determinar a equação geral da circunferência de centro C(2, -3) e raio r = 4.
A equação reduzida da circunferência é:
( x - 2 )2 +( y + 3 )2 = 16
Desenvolvendo os quadrados dos binômios, temos:
109

110. Geometria Analítica - Cônicas
Elipse
Considerando, num plano , dois pontos distintos, F1 e F2 , e sendo 2a um número real maior que a
distância entre F1 e F2, chamamos de elipse o conjunto dos pontos do plano tais que a soma das distâncias
desses pontos a F1 e F2 seja sempre igual a 2a.
Por exemplo, sendo P, Q, R, S, F1 e F2 pontos de um mesmo plano e F1F2 < 2a, temos:
A figura obtida é uma elipse.
Observações:
1ª) A Terra descreve uma trajetória elíptica em torno do sol, que é um dos focos dessa trajetória.
A lua em torno da terra e os demais satélites em relação a seus respectivos planetas também apresentam
esse comportamento.
2ª) O cometa de Halley segue uma órbita elíptica, tendo o Sol como um dos focos.
3ª) As elipses são chamadas cônicas porque ficam configuradas pelo corte feito em um cone circular reto por
um plano oblíquo em relação à sua base.
Elementos
Observe a elipse a seguir. Nela, consideramos os seguintes elementos:
• focos : os pontos F1 e F2
• centro: o ponto O, que é o ponto médio de
• semi-eixo maior: a
• semi-eixo menor: b
• semidistância focal: c
• vértices: os pontos A1, A2, B1, B2
• eixo maior:
• eixo menor:
• distância focal:
110

111. Relação fundamental
Na figura acima, aplicando o Teorema de Pitágoras ao tri6angulo OF2B2 , retângulo em O, podemos escrever
a seguinte relação fundamental:
a2 =b2 + c2
Excentricidade
Chamamos de excentricidade o número real e tal que:
Pela definição de elipse, 2c < 2a, então c < a e, conseqüentemente, 0 < e < 1.
Observação:Quando os focos são muito próximos, ou seja, c é muito pequeno, a elipse se aproxima de uma
circunferência.
Retas
Geometria analítica: retas
Introdução
Entre os pontos de uma reta e os números reais existe uma correspondência biunívoca, isto é, a cada ponto
de reta corresponde um único número real e vice-versa.
Considerando uma reta horizontal x, orientada da esquerda para direita (eixo), e determinando um ponto O
dessa reta ( origem) e um segmento u, unitário e não-nulo, temos que dois números inteiros e consecutivos
determinam sempre nesse eixo um segmento de reta de comprimento u:
Medida algébrica de um segmento
Fazendo corresponder a dois pontos, A e B, do eixo x os números reais xA e xB , temos:
A medida algébrica de um segmento orientado é o número real que corresponde à diferença entre as
abscissas da extremidade e da origem desse segmento.
Plano cartesiano
111

112. A geometria analítica teve como principal idealizador o filósofo francês René Descartes ( 1596-1650). Com o
auxílio de um sistema de eixos associados a um plano, ele faz corresponder a cada ponto do plano um par
ordenado e vice-versa.
Quando os eixos desse sistemas são perpendiculares na origem, essa correspondência determina um
sistema cartesiano ortogonal ( ou plano cartesiano). Assim, há uma reciprocidade entre o estudo da geometria (
ponto, reta, circunferência) e da Álgebra ( relações, equações etc.), podendo-se representar graficamente
relações algébricas e expressar algebricamente representações gráficas.
Observe o plano cartesiano nos quadros quadrantes:
Exemplos:
• A(2, 4) pertence ao 1º quadrante (xA > 0 e yA > 0)
• B(-3, -5) pertence ao 3º quadrante ( xB < 0 e yB < 0)
Observação: Por convenção, os pontos localizados sobre os eixos não estão em nenhum quadrante.
Distância entre dois pontos
Dados os pontos A(xA, yA) e B(xB, yB) e sendo dAB a distância entre eles, temos:
112

113. Aplicando o teorema de Pitágoras ao triângulo retângulo ABC, vem:
Como exemplo, vamos determinar a distância entre os pontos A(1, -1) e B(4, -5):
Razão de secção
Dados os pontos A(xA, yA), B(xB, yB), C(xC, yC) de uma mesma reta , o ponto C divide numa
determinada razão, denominada razão de secção e indicada por:
em que , pois se , então A = B.
Observe a representação a seguir:
Como o , podemos escrever:
Vejamos alguns exemplos:
113

114. • Considerando os pontos A(2, 3), B(5, 6) e P(3, 4), a razão em que o ponto P divide é:
Se calculássemos rp usando as ordenadas dos pontos, obteríamos o mesmo resultado:
• Para os pontos A(2, 3), B(5, 6) e P(1, 2), temos:
Assim, para um ponto P qualquer em relação a um segmento orientado contido em um eixo, temos:
• se P é interior a , então rp > 0
• se P é exterior a , então rp < 0
• se P = A, então rp =0
• se P = B, então não existe rp (PB = 0)
• se P é o ponto médio de , então rp =1
Ponto médio
114

115. Dados os pontos A(xA, yA), B(xB, yB) e P, que divide ao meio, temos:
Assim:
Logo, as coordenadas do ponto médio são dadas por:
Baricentro de um triângulo
Observe o triângulo da figura a seguir, em que M, N e P são os pontos médios dos lados ,
respectivamente. Portanto, são as medianas desse triângulo:
Chamamos de baricentro (G) o ponto de intersecção das medianas de um triângulo.
Esse ponto divide a mediana relativa a um lado em duas partes: a que vai do vértice até o baricentro tem o
dobro da mediana da que vai do baricentro até o ponto médio do lado.
Veja:
115

116. Cálculo das coordenadas do baricentro
Sendo A(XA, YA), B(XB, YB) e C(XC, YC) vértices de um triângulo, se N é ponto médio de , temos:
Mas:
Analogamente, determinamos . Assim:
Condições de alinhamento de três pontos
116

117. Se três pontos, A(xA, yA), B(xB, yB) e C(xC, yC), estão alinhados, então:
Para demonstrar esse teorema podemos considerar três casos:
a) três pontos alinhados horizontalmente
Neste caso, as ordenadas são iguais:
yA = yB = yC
e o determinante é nulo, pois a 2ª e a 3ª coluna são proporcionais.
b) três pontos alinhados verticalmente
Neste caso, as abscissas são iguais:
xA = xB = xC
e o determinante é nulo, pois a 1ª e a 3ª coluna são proporcionais.
c) três pontos numa reta não-paralela aos eixos
117

118. Pela figura, verificamos que os triângulos ABD e BCE são semelhantes. Então:
Desenvolvendo, vem:
Como:
então .
Observação: A recíproca da afirmação demonstrada é válida, ou seja, se , então os
pontos A(xA,yA), B(xB,yB) e C(xC, yC) estão alinhados.
Equações de uma reta
118

119. Equação geral
Podemos estabelecer a equação geral de uma reta a partir da condição de alinhamento de três pontos.
Dada uma reta r, sendo A(xA, yA) e B(xB, yB) pontos conhecidos e distintos de r e P(x,y) um ponto genérico,
também de r, estando A, B e P alinhados, podemos escrever:
Fazendo yA - yB = a, xB - xA = b e xAyB - xByA=c, como a e b não são simultaneamente nulos , temos:
ax + by + c = 0
(equação geral da reta r)
Essa equação relaciona x e y para qualquer ponto P genérico da reta. Assim, dado o ponto P(m, n):
• se am + bn + c = 0, P é o ponto da reta;
• se am + bn + c 0, P não é ponto da reta.
Acompanhe os exemplos:
• Vamos considerar a equação geral da reta r que passa por A(1, 3) e B(2, 4).
Considerando um ponto P(x, y) da reta, temos:
• Vamos verificar se os pontos P(-3, -1) e Q(1, 2) pertencem à reta r do exemplo anterior. Substituindo
as coordenadas de P em x - y + 2 = 0, temos:
-3 - (-1) + 2 = 0 -3 + 1 + 2 = 0
Como a igualdade é verdadeira, então P r.
Substituindo as coordenadas de Q em x - y + 2 = 0, obtemos:
1-2+2 0
Como a igualdade não é verdadeira, então Q r.
Equação segmentária
119

120. Considere a reta r não paralela a nenhum dos eixos e que intercepta os eixos nos pontos P(p, 0) e Q(0, q),
com :
A equação geral de r é dada por:
Dividindo essa equação por pq , temos:
Como exemplo, vamos determinar a equação segmentária da reta que passa por P(3, 0) e Q(0, 2), conforme
o gráfico:
Equações paramétricas
120

121. São equações equivalentes à equação geral da reta, da forma x= f(t) e y= g(t), que relacionam as
coordenadas x e y dos pontos da reta com um parâmetro t.
Assim, por exemplo, , são equações paramétricas de uma reta r.
Para obter a equação geral dessa reta a partir das paramétricas, basta eliminar o parâmetro t das duas
equações:
x=t+2 t = x -2
Substituindo esse valor em y = - t + 1, temos:
y = -(x - 2) + 1 = -x + 3 x + y - 3 = 0 ( equação geral de r)
Equação Reduzida
Considere uma reta r não-paralela ao eixo Oy:
Isolando y na equação geral ax + by + c = 0, temos:
Fazendo , vem:
y = mx + q
Chamada equação reduzida da reta, em que fornece a inclinação da reta em relação ao eixo Ox.
Quando a reta for paralela ao eixo Oy, não existe a equação na forma reduzida.
Coeficiente angular
121

122. Chamamos de coeficiente angular da reta r o número real m tal que:
O ângulo é orientado no sentido anti-horário e obtido a partir do semi-eixo positivo Ox até a reta r. Desse
modo, temos sempre .
Assim:
• para ( a tangente é positiva no 1º quadrante)
• para ( a tangente é negativa no 2º quadrante)
Exemplos:
122

123. Determinação do coeficiente angular
Vamos considerar três casos:
a) o ângulo é conhecido
b) as coordenadas de dois pontos distintos da reta são conhecidas: A(xA, yA) e B(xB, yB)
Como ( ângulos correspondentes) temos que . Mas, m = tg Então:
Assim, o coeficiente angular da reta que passa, por exemplo, por A(2, -3) e B(-2, 5) é:
c) a equação geral da reta é conhecida
123

124. Se uma reta passa por dois pontos distintos A(XA, YA) e B(XB, YB), temos:
Aplicando o Teorema de Laplace na 1ª linha, vem:
(YA - YB)x + (XB - XA)y + XAYA - XBYB = 0
Da equação geral da reta, temos:
Substituindo esses valores em , temos:
Equação de uma reta r, conhecidos o coeficiente angular e um ponto de r
Seja r uma reta de coeficiente angular m. Sendo P(X0, Y0), P r, e Q(x,y) um ponto qualquer de r(Q P),
podemos escrever:
Como exemplo, vamos determinar a equação geral da reta r que passa por P(1, 2), sendo m=3. Assim, temos
X0=1 e Y0=2. Logo:
y-y0=m(x-x0)=y-2 = 3(x - 1) = y-2 = 3x - 3 = 3x - y - 1 = 0
que é a equação geral de r.
Representação gráfica de retas
Para representar graficamente as retas de equação ax + by + c = 0 ( b 0), isolamos a variável y e
atribuímos valores a x, obtendo pares ordenados que são pontos da reta.
Assim, é mais conveniente usar a equação na forma reduzida, já que ela apresenta o y isolado.
124

125. Coordenadas do ponto de intersecção de retas
A intersecção das retas r e s, quando existir, é o ponto P(x, y), comum a elas, que é a solução do sistema
formado pelas equações das duas retas.
Vamos determinar o ponto de intersecção, por exemplo, das retas r: 2x +y - 4 =0 e s: x -y +1=0. Montando o
sistema e resolvendo-o, temos:
Substituindo esse valor em x -y = -1, temos:
1 - y = -1
y=2
Logo, P(1, 2) é o ponto de intersecção das retas r e s.
Graficamente, temos:
Posições relativas entre retas
Paralelismo
Duas retas, r e s, distintas e não-verticais, são paralelas se, e somente se, tiverem coeficientes angulares
iguais.
125