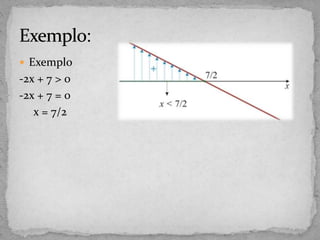
O documento explica como resolver inequações do primeiro grau, inequações produto e inequações quociente. Para resolver inequações do primeiro grau, iguala-se a expressão a zero e estuda-se o sinal. Para resolver inequações produto e quociente, determina-se as funções envolvidas, suas raízes e sinal para verificar a condição imposta pela inequação. Exemplos ilustram cada tipo de resolução.

1. Pausa matemática

2.  A equação é caracterizada pelo sinal da igualdade (=).
A inequação é caracterizada pelos sinais de maior
(>), menor (<), maior ou igual (≥) e menor ou igual (≤).

3.  Pode-se resolver qualquer inequação do 1°
grau por meio do estudo do sinal de uma
função do 1° grau, com o seguinte
procedimento:
 1. Iguala-se a expressão ax + b a zero;
 2. Localiza-se a raiz no eixo x;
 3. Estudar-se o sinal conforme o
caso.
 .

4.  Exemplo
-2x + 7 > 0
-2x + 7 = 0
x = 7/2

5.  Resolver uma inequação produto consiste em
encontrar os valores de x que satisfazem a condição
estabelecida pela inequação. Para isso utilizamos o
estudo do sinal de uma função. Observe a resolução da
seguinte equação produto: (2x + 6)( –3x + 12) > 0.

6.  Vamos estabelecer as seguintes funções:
 y1= 2x + 6 e y2= –3x + 12.
 Determinando a raiz da função (y = 0) e a posição da reta (a > 0
crescente e a < 0 decrescente).
Verificando o sinal da inequação produto (2x + 6)(–3x + 12) > 0.
Observe que a inequação produto exige a seguinte condição: os
possíveis valores devem ser maiores que zero, isto é, positivo.

7.  Na resolução da inequação quociente utilizamos os
mesmos recursos da inequação produto, o que
difere é que, ao calcularmos a função do
denominador, precisamos adotar valores maiores
ou menores que zero e nunca igual a zero.

8.  Observe a resolução da seguinte inequação quociente
 Resolver as funções y1= x + 1 e y2= 2x –1, determinando
a raiz da função (y = 0) e a posição da reta(a > 0
crescente e a < 0 decrescente).