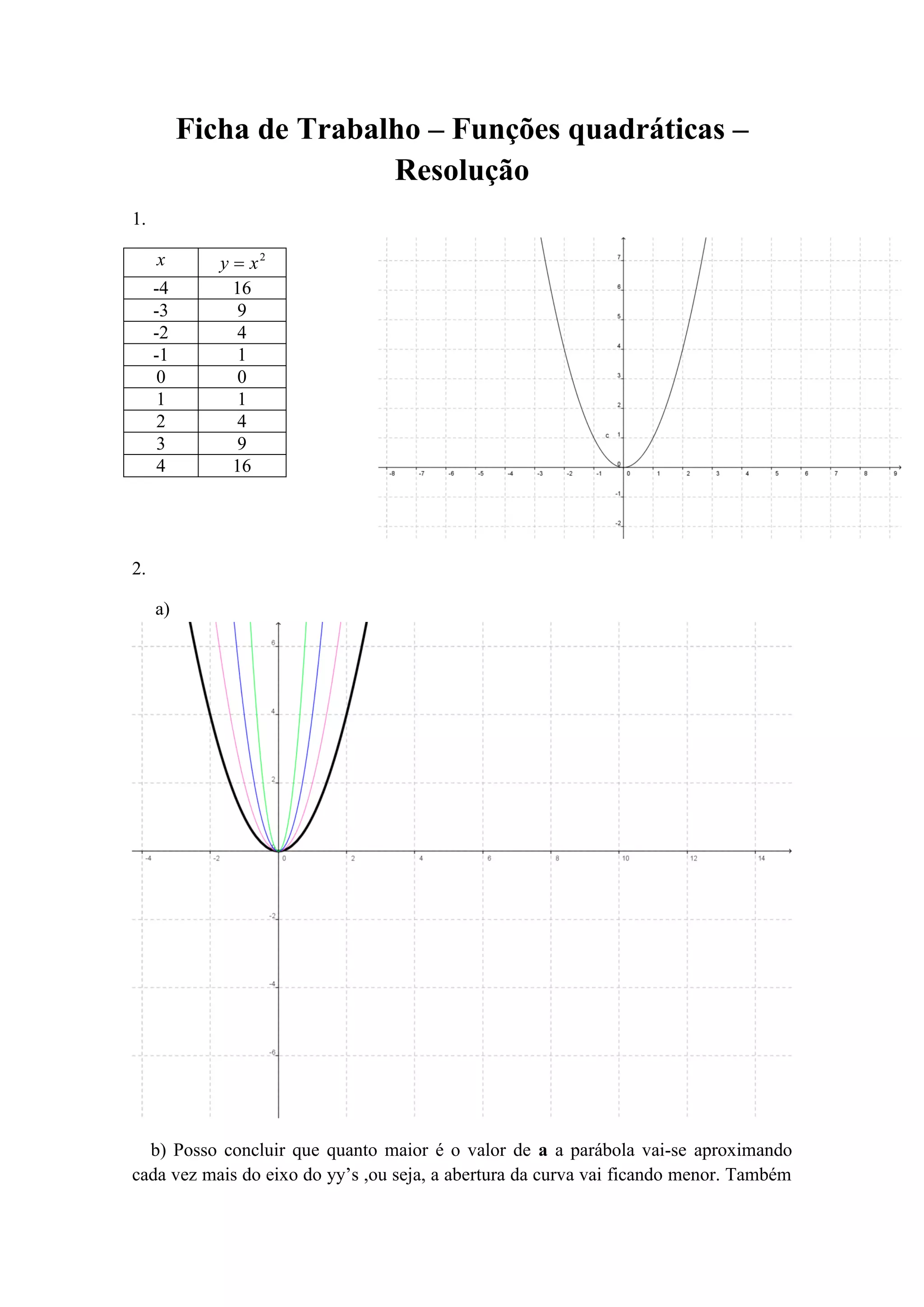
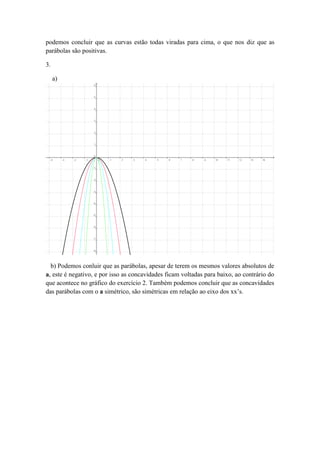
O documento descreve as características de funções quadráticas. Explica que quando o parâmetro a é positivo, as parábolas ficam voltadas para cima, e quando é negativo, ficam voltadas para baixo. Também indica que quando o valor absoluto de a aumenta, a curva se aproxima do eixo y, e quando diminui, a curva se afasta do eixo y.

1. Ficha de Trabalho – Funções quadráticas –
Resolução
1.
x y  x2
-4 16
-3 9
-2 4
-1 1
0 0
1 1
2 4
3 9
4 16
2.
a)
b) Posso concluir que quanto maior é o valor de a a parábola vai-se aproximando
cada vez mais do eixo do yy’s ,ou seja, a abertura da curva vai ficando menor. Também

2. podemos concluir que as curvas estão todas viradas para cima, o que nos diz que as
parábolas são positivas.
3.
a)
b) Podemos conluir que as parábolas, apesar de terem os mesmos valores absolutos de
a, este é negativo, e por isso as concavidades ficam voltadas para baixo, ao contrário do
que acontece no gráfico do exercício 2. Também podemos concluir que as concavidades
das parábolas com o a simétrico, são simétricas em relação ao eixo dos xx’s.

3. 4. Uma parábola é o nome da curva que representa um gráfico de uma função
quadrática.
A função quadrática ax2 é incompleta, porque faltam os termos de grau 1 e 0, e neste
caso o vértice da parábola corresponde à origem do referencial.
Quando o parâmetro a é positivo as concavidades das parábolas ficam voltadas para
cima, ou seja, o valor da imagem é sempre positivo, mas quando o objeto é zero, o valor
absoluto de a também é zero. E quando o parâmetro a é negativo as concavidades ficam
voltadas para baixo, ou seja, o valor da imagem é negativo, ou zero se o objeto for zero.
Neste caso, o valor de a corresponde à imagem dos objetos -1 e 1. Este valor de a nunca
poderá ser igual a zero, uma vez que nesse caso a função passaria a ser uma função
constante do tipo y=0, que coincide graficamente com o eixo das abcissas.
As parábolas são simétricas ao eixo dos yy’s, independentemente do valor absoluto de a
ser negativo ou positivo.
Quando existem parábolas voltadas para baixo e voltadas para cima no mesmo gráfico,
e estas têm o mesmo valor absoluto de a, podemos verificar que são simétricas em
relação ao eixo dos xx’s.
Também concluímos que quando o valor do parâmetro a aumenta, a abertura da curva
diminui, ou seja, aproxima-se do eixo dos yy’s. E quando o valor do parâmetro a
diminui, em valor absoluto, a abertura da curva aumenta, afastando-se do eixo dos yy’s
e aproximando-se do dos xx’s.