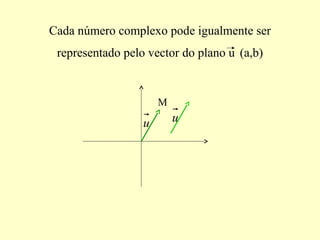
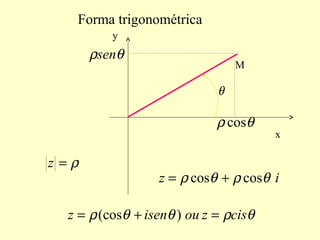
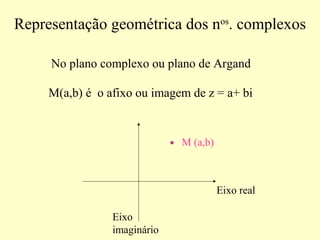
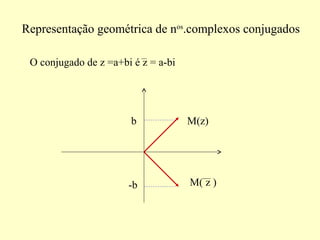
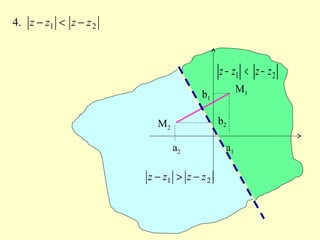
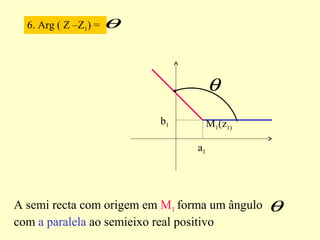
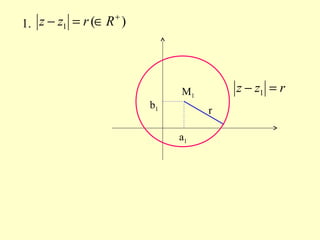
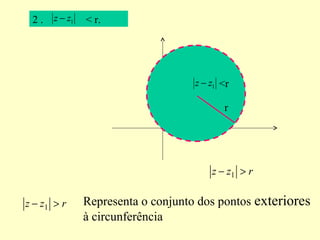
1) O documento descreve a representação e operações com números complexos, incluindo sua forma algébrica como a + bi, representação geométrica no plano complexo, módulo, argumento e formas trigonométrica e algébrica. 2) Apresenta a representação geométrica de números complexos e suas operações como conjugação e subtração no plano complexo. 3) Explica a interpretação geométrica de diferentes condições envolvendo distâncias e ângulos entre números complexos no plano.

1. Números Complexos
Chama-se nº. Complexo ao nº. na
forma a+bi,em que a,b∈ℜ e i2
=-1
A escrita z = a+bi é a forma algébrica do complexo
a é a parte real de z, Re (z) = a
b é o coeficiente da parte imaginária de z, Im (z) =b

2. Representação geométrica dos nos
. complexos
No plano complexo ou plano de Argand
M (a,b)
Eixo real
Eixo
imaginário
M(a,b) é o afixo ou imagem de z = a+ bi

3. Cada número complexo pode igualmente ser
representado pelo vector do plano u (a,b)
M
u u

4. Representação geométrica de –z
Sendo z = a+bi então –z = -a-bi
M(z)
M(-z)

5. Representação geométrica de nos
.complexos conjugados
O conjugado de z =a+bi é z = a-bi
b
-b
M(z)
M( z )

6. Representação trigonométrica dos números complexos
Modulo de z = a+bi é
22
baz +=
22
baz +=
Argumento de z é a medida do ângulo orientado ( )
.
,
.
OYXO
A expressão geral dos argumentos é:
Argz = ∈+ kk ,2πθ z

7. M
O x
y
a
b
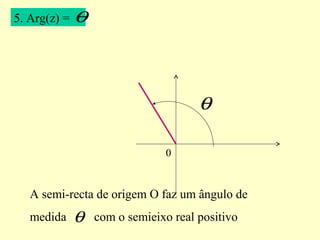
θ
ZOM =
] ]πθ 2,0∈ Chama-se argumento positivo mínimo

8. Forma trigonométrica
x
y
M
θ
θρ cos
θρsen
ρ=z
iz θρθρ coscos +=
θρθθρ ciszouisenz =+= )(cos

9. Representemos na forma trigonométrica o
complexo:z = - i+3
3
3
3
1
213
−=
−
=
=+=
θtg
z
A imagem de z é do 2º Q
E é 6
5π
θ =
θ
M (z)

10. Domínios planos
O módulo de como distância1zz −
M(z2)
Consideremos M1e M2
afixos de z1 e z2
M(z1)
M(z2-z1)
M-(z1)
Como 12 zzOM −=
Então é a
distância entre z1 z2
12 zz −

11. Designemos por z a variável complexa
E z1 e z2 dois números complexos de
afixos M1 e M2 respectivamente
Procuremos interpretar as seguintes
condições em C:

12. 1. )(1
+
∈=− Rrzz
r
M1
a1
b1
rzz =− 1

13. 2 . < r.1zz −
1zz − <r
r
rzz >− 1
rzz >− 1
Representa o conjunto dos pontos exteriores
à circunferência

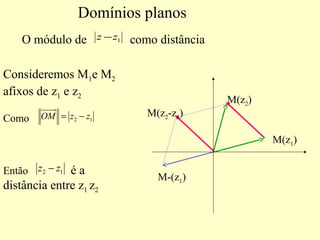
14. 21.3 zzzz −=−
21 zzzz −=−
21 zzzz −=− Trata-se da mediatriz do segmento [ ]21, MM
M1
M2
b1
a1a2
b2

15. 21.4 zzzz −<−
M1
M2
b1
a1a2
b2
21 zzzz −>−
21 zzzz −<−

16. 5. Arg(z) = θ
θ
0
A semi-recta de origem O faz um ângulo de
medida com o semieixo real positivoθ

17. 6. Arg ( Z –Z1) = θ
θ
a1
b1 M1(z1)
A semi recta com origem em M1 forma um ângulo
com a paralela ao semieixo real positivo
θ