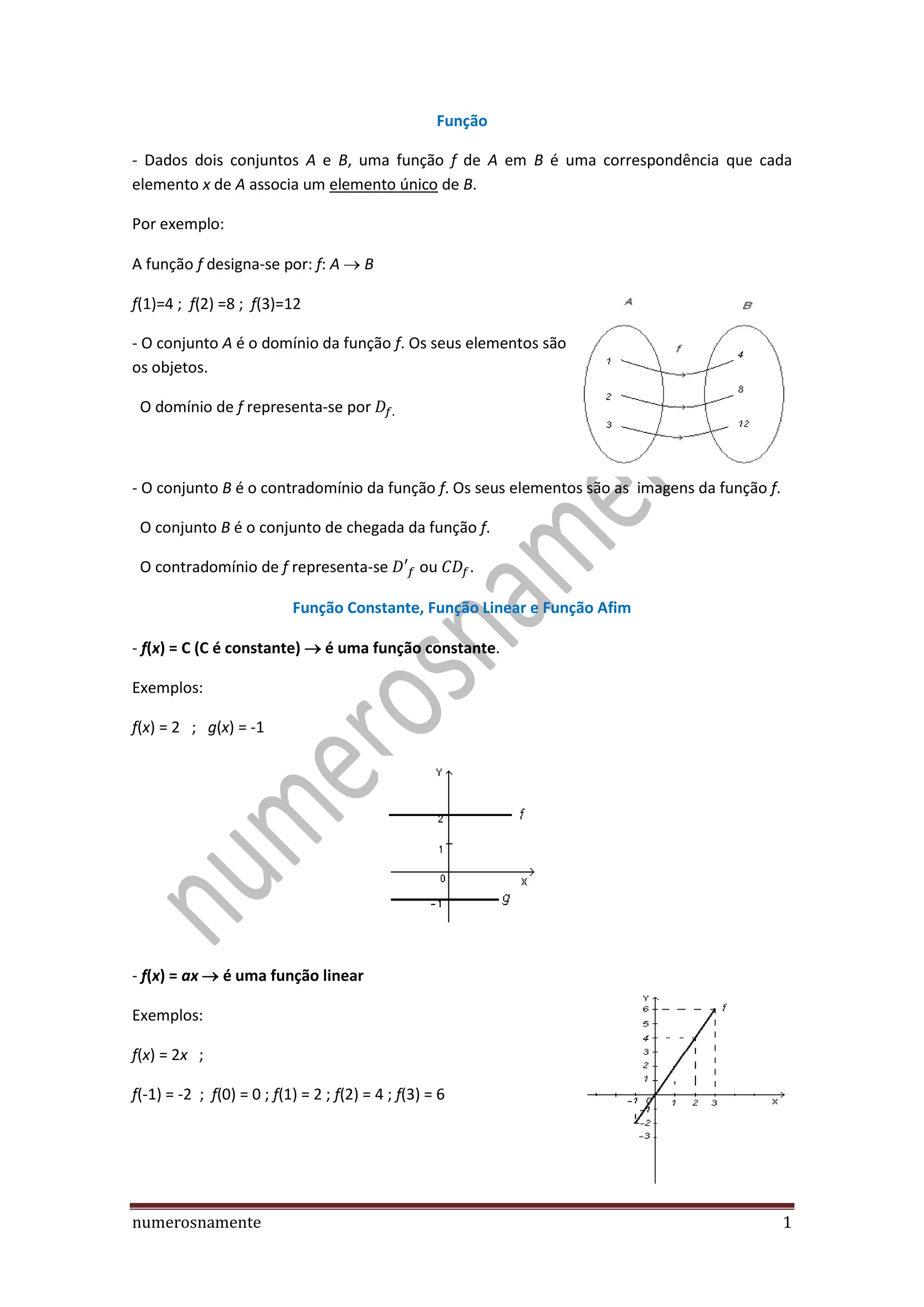
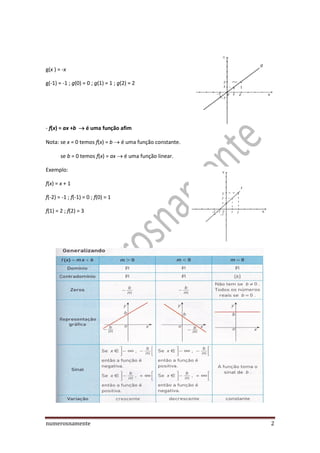
O documento descreve funções matemáticas, incluindo definições de funções, domínio, contradomínio, funções constantes, lineares e afins. Ele também aborda propriedades de funções, como injetividade, sobrejetividade e bijetividade, além de exemplificar funções compostas e permutáveis. Por fim, discute a condição para uma função ter uma inversa, que é ser bijetiva.

1. numerosnamente 1
Função
- Dados dois conjuntos A e B, uma função f de A em B é uma correspondência que cada
elemento x de A associa um elemento único de B.
Por exemplo:
A função f designa-se por: f: A  B
f(1)=4 ; f(2) =8 ; f(3)=12
- O conjunto A é o domínio da função f. Os seus elementos são
os objetos.
O domínio de f representa-se por
- O conjunto B é o contradomínio da função f. Os seus elementos são as imagens da função f.
O conjunto B é o conjunto de chegada da função f.
O contradomínio de f representa-se ou .
Função Constante, Função Linear e Função Afim
- f(x) = C (C é constante)  é uma função constante.
Exemplos:
f(x) = 2 ; g(x) = -1
- f(x) = ax  é uma função linear
Exemplos:
f(x) = 2x ;
f(-1) = -2 ; f(0) = 0 ; f(1) = 2 ; f(2) = 4 ; f(3) = 6

2. numerosnamente 2
g(x ) = -x
g(-1) = -1 ; g(0) = 0 ; g(1) = 1 ; g(2) = 2
- f(x) = ax +b  é uma função afim
Nota: se x = 0 temos f(x) = b  é uma função constante.
se b = 0 temos f(x) = ax  é uma função linear.
Exemplo:
f(x) = x + 1
f(-2) = -1 ; f(-1) = 0 ; f(0) = 1
f(1) = 2 ; f(2) = 3

3. numerosnamente 3
Função real de varável real
- Uma função real de variável real é uma função cujo domínio e o conjunto de chagada estão
contidos em.
- Para caracterizar uma função real de variável real, f, tem-se de identificar o domínio, A, e o
seu conjunto de chegada, B, e identificar uma expressão analítica de f(x):
f : A  B
x  f(x)
Domínio de uma função real de variável real
- Uma função real de variável real é uma função se o seu domínio estiver contido em .
- Vamos considerar vários exemplos de funções em que se tem de definir o seu domínio por
forma a serem válidas em :
1- ( ) ; *  +
2- ( ) ; *  +
3- ( ) ; nota que a expressão só é válida se ; *  +  * +
4- ( ) ; *  +  * +
5- ( ) ; *  +  * +
6- ( ) ; *  +
7- ( ) ; nota que *  +
8- ( ) ; c.a: √ ; então temos que
*  + = {-2,+2} ou
9- ( ) √ ; se n = par tem-se: a  0 ; se n = impar tem-se: 
10- ( ) √ ; *   +
Nota que: 3
11- ( ) √ ; *  +
12- ( )
√
; se n é par: b  0 ; se n é impar: b
13- ( )
√
; *   +
Nota que:   3

4. numerosnamente 4
Função Injetiva, Sobrejetiva e Bijetiva
-Uma função f é injetiva se a cada elemento do domínio corresponde uma e só uma imagem
distinta.
Na figura tem-se que cada elemento do conjunto A (domínio)
através da função f, origina uma imagem no conjunto B
(conjunto de chegada=contradomínio).
Assim a função f é injetiva.
Simbolicamente:
f : A B é injetiva se e somente se:
 ( ) ( )
-Uma função f é sobrejetiva se qualquer elemento do conjunto de chegada B é uma imagem
de, pelo menos, um elemento do conjunto A (objecto).
Na figura ao lado temos que o * + = A
O Conjunto de chegada B = * +
O contradomínio é igual ao conjunto B, logo a função f é
sobrejetiva.
Também verificamos que a função f é não injetiva, pois
( ) ( )
Considere a figura ao lado:
A função g é não sobrejetiva, pois:
O conjunto de chegada = D ={4,8,12,16}.
O contradomínio da função g = {4,8,12}.
Tem-se que {4,8,12,16} {4,8,12} ( ) não sobrejetiva.

5. numerosnamente 5
- Uma função é bijetiva se for simultaneamente injetiva e sobrejetiva
Na figura ao lado, a função g é injetiva e é sobrejetiva. Assim a
função g é bijetiva.
Em análise sabe-se que a função g é injetiva pois a cada
objecto do conjunto C corresponde uma e só uma imagem no
conjunto D.
A função g é sobrejetiva pois o conjunto de chegada
(D={5,10,15}) é igual ao contradomínio da função = {5,10,15}.
Logo conclui-se que g é uma função bijetiva.
Considere a figura ao lado onde está representada a função h.
A função h é injetiva (a cada objecto do conjunto M corresponde
uma e só uma imagem do conjunto N.
A função h é não sobrejetiva (o conjunto de chegada é {5,10,15}
Assim s conclui que a função h não é bijetiva.
Função Composta
- A função composta de f com g é a função
Dadas duas funções, g :   , a função composta de f com g é a função :
 , talque:
{ ( ) + e  , ( )( ) ( ( ))
Por exemplo:
Consideremos as funções f , g e h , de  em , definidas por:
( ) ; ( ) e ( ) ( )
Vamos calcular ( )( )
( )( ) ( ( )) = ( ) ; {  ( )  + = 

6. numerosnamente 6
Vamos calcular ( )( )
( )( ) ( ( )) = (( ) ) ( ) ; {  ( )  + = 
Vamos calcular ( )( )
( )( ) ( ( )) = (( ) ) ( ) ; {  ( )  + = 
Funções Permutáveis
- Duas funções são permutáveis quando
Por exemplo: Sejam ( ) ( ) duas funções reais de variável real.
( )( ) ( ( )) ( )
( )( ) ( ( )) ( )
As funções e são permutáveis.
Função Inversa
- Uma função admite inversa se for bijetiva.
Por exemplo, considere as funções reais de variável real, ( ) e ( )
Para a função sabe-se que:
  ; é uma função afim, logo é injetiva e sobrejetiva. Assim admite inversa.
A sua inversa é:
; ( )
Para a função sabe-se que:
 ; é uma função quadrática cuja imagem é uma parábola, logo é
não injetiva. Assim a função não admite inversa.