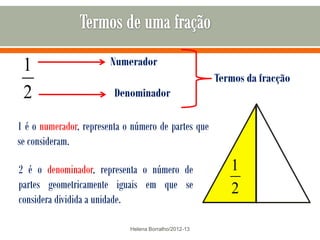
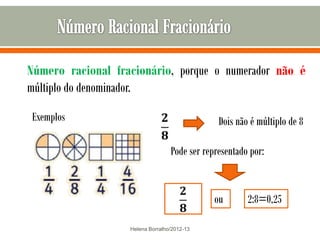
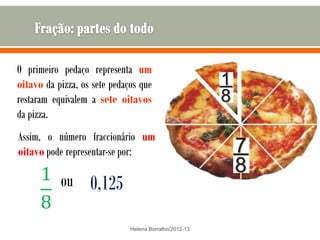
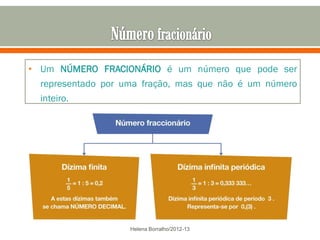
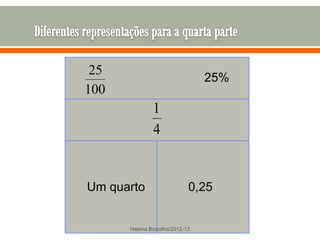
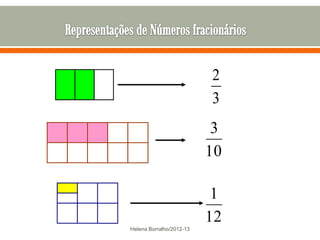
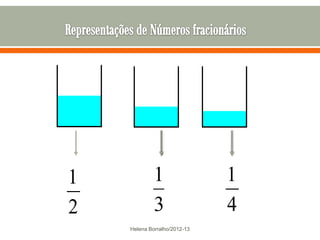
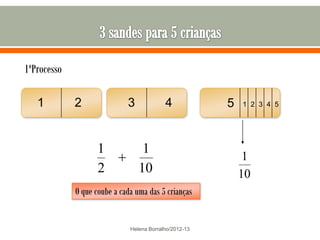
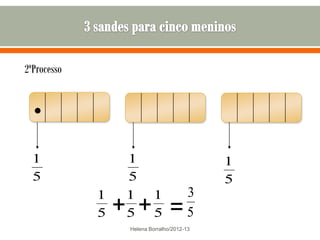
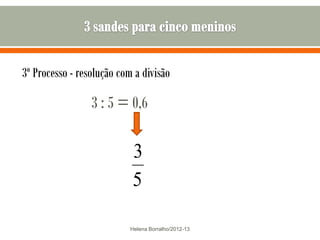
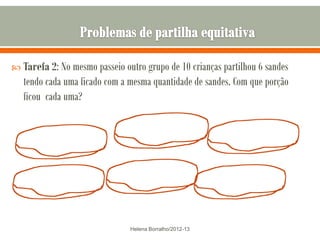
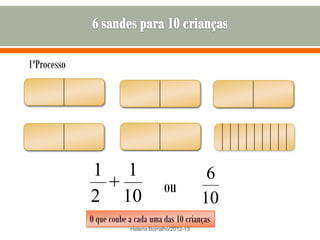
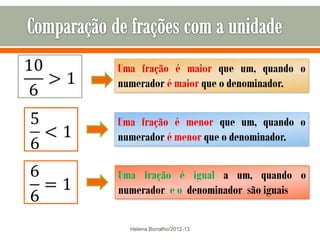
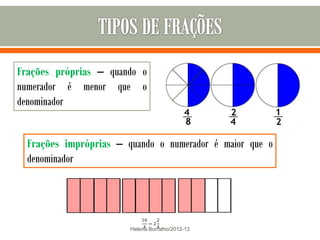
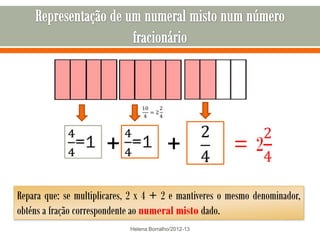
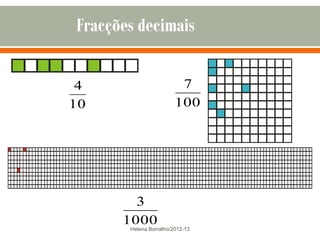
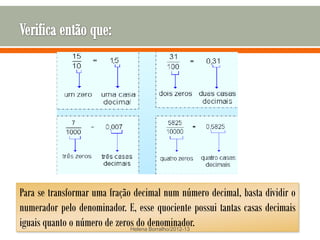
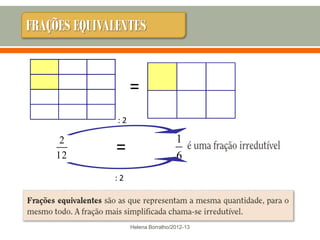
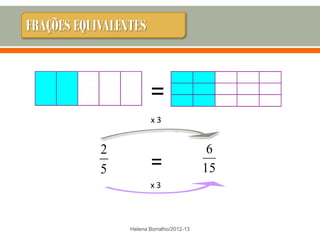
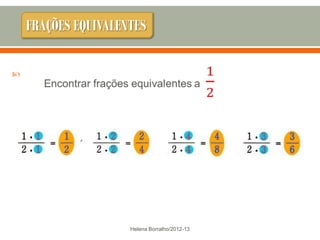
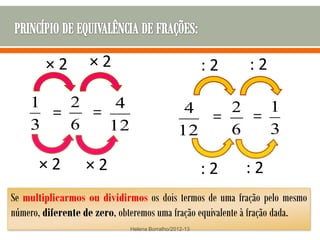
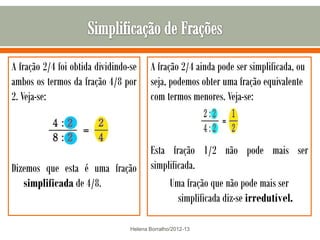
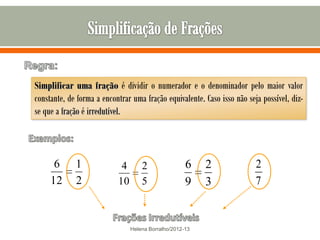
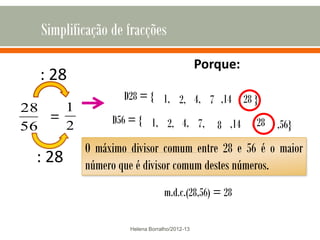
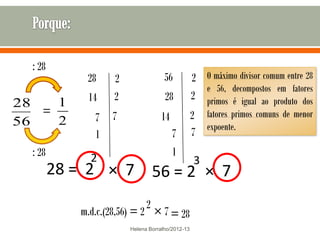
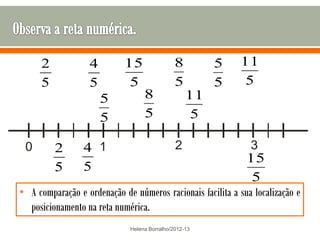
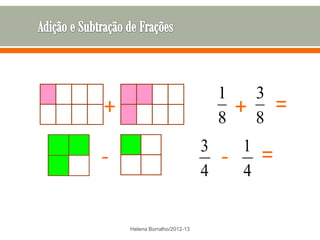
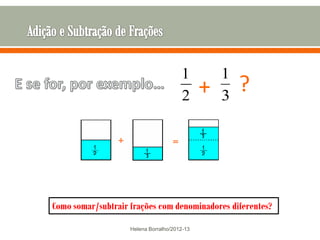
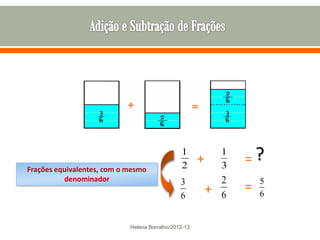
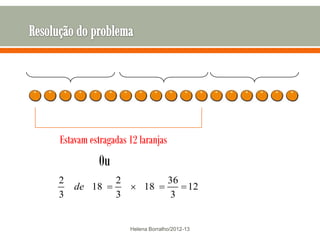
O documento discute os números racionais, incluindo frações, números fracionários e decimais. Explica que uma fração representa uma ou mais partes de uma unidade dividida em partes iguais e define os termos numerador e denominador. Também define o conjunto dos números racionais Q e explica como todo número racional pode ser representado por uma fração.