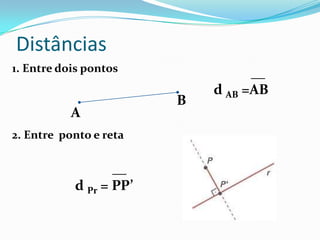
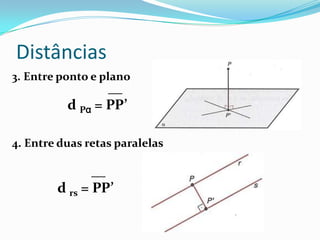
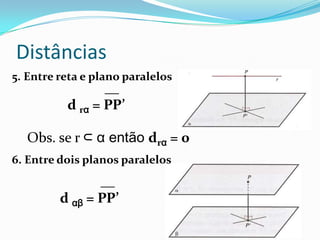
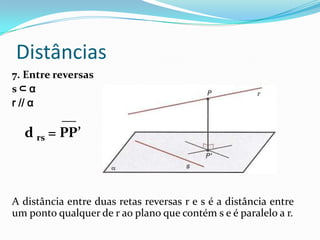
1. O documento discute vários tipos de distâncias geométricas, como entre pontos, pontos e retas/planos, retas e planos, e fornece exemplos de como calcular cada uma. 2. Dois exercícios pedem para calcular distâncias dadas informações sobre pontos e suas projeções em retas e planos. 3. Um terceiro exercício pede a distância entre pontos A e D dados segmentos perpendiculares.

1. MATEMÁTICA - 1
Ten Villa Nova
CMCG -2012

2. Distâncias
1. Entre dois pontos __
d AB =AB
B
A
2. Entre ponto e reta
__
d Pr = PP’

3. Distâncias
3. Entre ponto e plano
__
d Pα = PP’
4. Entre duas retas paralelas
__
d rs = PP’

4. Distâncias
5. Entre reta e plano paralelos
__
d rα = PP’
Obs. se r ⊂ α então drα = 0
6. Entre dois planos paralelos
__
d αβ = PP’

5. Distâncias
7. Entre reversas
s⊂α
r // α
__
d rs = PP’
A distância entre duas retas reversas r e s é a distância entre
um ponto qualquer de r ao plano que contém s e é paralelo a r.

6. Exercícios __
1. Sejam os pontos B, C e __ plano α tais que BC mede 5 cm,
um
a projeção ortogonal de BC sobre α mede 3 cm e o ponto C
pertence a α. Qual é a distância do ponto B ao plano α?
4 cm

7. Exercícios
2. Considere um plano sobre o qual estão localizados os
pontos X, Y, Z e W, de forma que:
I. X, Y e Z são colineares;
II. as retas WX e YZ são perpendiculares;
III. X é um ponto exterior ao segmento YZ;
IV. a distância YZ é 90 cm;
V. os ângulos WZX e WYX medem respectivamente, 45° e
60°.
Então determine a distância ZX.
135+ 45√3 cm

8. Exercícios
 3. Seja um plano α, e um segmento AB perpendicular a
esse plano, com B ∈ α. CD e BC estão contidos nesse
plano e CD é perpendicular a BC. Se AB = 5 cm, BC =
4 cm, e CD = 3 cm, determine, em cm, a distância de A
a D.
5√2 cm