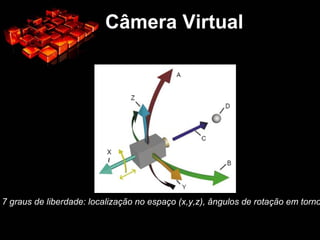
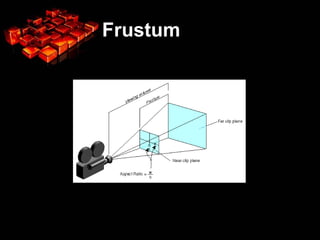
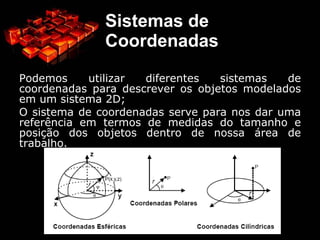
O documento discute transformações geométricas em computação gráfica, incluindo translação, escala e rotação. Explica como matrizes são usadas para representar essas transformações e como elas afetam os pontos e objetos. Também aborda conceitos como sistemas de coordenadas, câmera virtual, frustum e suas implementações em OpenGL.

1. Computação Gráfica Aula 6 – Transformações Geométricas no Plano e no Espaço Prof. Tony Alexander Hild Documento licenciado por Creative Commons - http://creativecommons.org/licenses/by-nc-sa/2.5/br/

2. Introdução Transformações geométricas são operações que podem ser utilizadas visando a alteração de algumas características como posição, orientação, forma ou tamanho do objeto a ser desenhado.

3. Todas as transformações geométricas podem ser representadas na forma de equações;

4. O problema é que manipulações de objetos gráficos normalmente envolvem muitas operações de aritmética simples;

5. As matrizes são muito usadas nessas manipulações porque são mais fáceis de usar e entender do que as equações algébricas, o que explica por que programadores e engenheiros as usam extensivamente. Matrizes em Computação Gráfica

6. Pontos, Vetores e Matrizes Dado um sistema de coordenadas, é possível definir pontos e objetos neste sistema pelas suas coordenadas;

7. Nos espaços bidimensionais ou nos objetos planos, duas coordenadas caracterizam um ponto;

8. Para objetos tridimensionais ou pontos no espaço, três coordenadas são necessárias para definir seu posicionamento;

9. Assim, dado um sistema de coordenadas, cada ponto pode ser associado às suas coordenadas no sistema. Por exemplo:

10. Relembrando - Vetores e matrizes podem ser processados por operações aritméticas como as que fazemos com os números.

11. Adição e subtração: os respectivos elementos dos dois vetores são somados formando um novo vetor. Ex.: [1 1 1] + [2 2 2] = [3 3 3] Multiplicação por valor constante. Ex.: 3 x [1 2 3] = [3 6 9] Transposição: Resulta da troca dos valores das linhas de um vetor ou matriz, por suas colunas. Ex.: Multiplicação de Matrizes: Sendo o número de linhas da primeira igual ao número de colunas da segunda pode-se multiplicá-las. O resultado se dará pela soma dos produtos dos elementos das linhas da primeira pelos elementos da coluna da segunda, em uma matriz com o número de linhas da primeira e o números de colunas da segunda. Ex.: Aritmética de Vetores e Matrizes

12. Podemos utilizar diferentes sistemas de coordenadas para descrever os objetos modelados em um sistema 2D;

13. O sistema de coordenadas serve para nos dar uma referência em termos de medidas do tamanho e posição dos objetos dentro de nossa área de trabalho. Sistemas de Coordenadas

14. Transformações em Pontos e Objetos A habilidade de representar um objeto em várias posições no espaço é fundamental para compreender sua forma;

15. A possibilidade de submetê-lo a diversas transformações é importante em diversas aplicações da computação gráfica;

16. As operações lineares de rotação e translação de objetos são chamadas operações de corpos rígidos;

17. A seguir veremos algumas transformações em 2D e 3D.

18. Transformação de Translação Transladar significa movimentar o objeto;

19. É possível efetuar a translação de pontos no plano (x,y) adicionando quantidades às suas coordenadas;

20. Assim, cada ponto em (x,y) pode ser movido por Tx unidades em relação ao eixo x , e por Ty unidades em relação ao eixo y;

21. Logo, a nova posição do ponto (x,y) passa a ser (x’,y’).

22. Transformação de Translação Translação de um triângulo de três unidades na horizontal e –4 na vertical. Repare que se teria o mesmo efeito transladando a origem do sistema de coordenadas para o ponto (–3, 4) na primeira figura.

23. Transformação de Escala Escalonar significa mudar as dimensões de escala;

24. Para fazer com que uma imagem definida por um conjunto de pontos mude de tamanho, teremos de multiplicar os valores de suas coordenadas por um fator de escala;

25. Transformar um objeto por alguma operação nada mais é do que fazer essa operação com todos os seus pontos. A mesma figura antes e depois de uma mudança de escala genérica, de ½ na horizontal e 1/4 na vertical. Repare que esse mesmo efeito relativo seria conseguido mudando a escala do sistema de eixos para uma outra que fosse o dobro da primeira na horizontal e quatro vezes maior na vertical.

26. Transformação de Rotação Rotação de um ponto P em torno da origem, passando para a posição P’. Repare que se chegaria a esse mesmo ponto através de uma rotação de – no sistema de eixos XY.

27. Transformação de Rotação Rotacionar significa girar;

28. Se um ponto de coordenada (x,y), distante r =( x ² +y² ) 1/2 da origem do sistema de coordenadas, for rotacionado de um ângulo θ em torno da origem, suas coordenadas, que antes eram definidas como: x = r * cos( Ф ), y = r * sen ( Ф ), passam a ser descritas como (x’, y’) dadas por: x’ = r . cos( θ + Ф ) = r . cos Ф . cos θ – r . sen Ф . sen θ y’ = r . sen( θ + Ф ) = r . sen Ф . cos θ + r . cos Ф . Sen θ isso equivale às expressões: x’ = x cos ( θ ) – y sen ( θ ) y’ = y cos ( θ ) + x sen ( θ ) Essas expressões podem ser descritas pela multiplicação do vetor de coordenadas do ponto (x y) pela matriz:

29. Transformação de Rotação Essa matriz é denominada matriz de rotação no plano xy por um ângulo . No caso de o objeto não estar definido na origem do sistema de coordenadas, a multiplicação de suas coordenadas por uma matriz de rotação também resulta em uma translação.

30. Regra da mão direita Para lembrar a direção dos eixos x, y e z, use a regra da mão direita: Mantenha sua mão posicionada de forma que consiga ver a palma de frente, com seus dedos voltados para cima;

31. Então abra o polegar para a direita, mantenha o indicador para cima, e aponte o dedo médio apontando para você;

32. Seu dedo indicador aponta para y positivo, seu dedo médio aponta para z positivo, e o polegar para x positivo;

33. As direções opostas representam x, y e z negativos.

34. Ângulos de Euler Os ângulos de Euler facilitam uma definição precisa das rotações em relação a um sistema de eixos;

35. Esses ângulos definem a rotação em um plano pelo giro em torno de um vetor normal a esse plano; + Yaw

36. Ângulos de Euler PITCH YAW ROLL

37. A fotografia que se obtém com uma máquina fotográfica real é uma projeção da cena em um plano, que corresponde ao filme;

38. Da mesma forma que no mundo real, a imagem que se obtém da cena sintética depende de vários fatores que determinam como esta é projetada em um plano para formar a imagem 2D exibida em algum dispositivo, como, por exemplo, o vídeo.

39. Ao gerar imagens de cenas 3D em computação gráfica, é comum fazermos uma analogia com uma máquina fotográfica;

40. Nessa analogia, imaginamos um observador que, posicionado em um ponto de observação, vê a cena através das lentes de uma câmera virtual que pode ser posicionada de forma a obter a imagem da cena, e onde pode-se definir, além da posição da câmera, sua orientação e foco, o tipo de projeção usada e a posição dos planos que limitam a visibilidade da cena, os chamados clipping planes. Câmera Virtual

41. Câmera Virtual Coordenadas da posição da câmera, e seus 7 graus de liberdade: localização no espaço (x,y,z), ângulos de rotação em torno de cada um dos eixos (setas curvas) e foco.

42. Em computação gráfica, o volume de visão ou view frustum é a região do espaço no mundo modelado que aparecerá na tela. É o campo de visão da câmera O formato exato desta região varia dependendo do tipo de lentes simuladas pela câmera, mas tipicamente é um volume de uma piramide retangular. Os planos que cortam o frustum perpendicularmente a direção da visão são chamados de plano próximo (near plane) e plano distante (far plane). Objetos mas próximos a câmera do que o plano próximo ou depois do plano distante não são desenhados. Geralmente, o plano distante é localizado infinitamente distante da câmera então todos os objetos do frustum são desenhados independentemente da distância da câmera. Frustum

43. Frustum

44. Viewing Frustum Culling Viewing frustum culling é o processo de remover totalmente do processo de renderização os objetos que se encontram fora do viewing frustum. Renderizar estes objetos seria uma perda de tempo visto que eles não são diretamente visíveis. Em ray tracing, viewing frutum culling não pode ser executado por que objetos fora do viewing frustum podem ser visíveis quando refletidos em um objeto dentro do frustum.

45. Transformações Geométricas com Opengl Os vértices que definem as primitivas geométricas são definidos no OpenGL em um sistema de eixos ortogonais orientados segundo a regra da mão direita. O eixo x será horizontal e orientado da esquerda para a direita, enquanto o eixo y será vertical, orientado de baixo para cima.

46. Transformação de Translação O comando para a translação é glTranslate( TYPE x, TYPE y, TYPE z) e tem como parâmetros as distâncias em cada um dos eixos coordenados. Por exemplo, para mover o ponto de visão ao longo do eixo z de 5 unidades, usa-se: glTranslatef(0.0f,0.0f,-5.0f); A seqüência de comandos para mover todos os pontos deumobjeto, é dada pelas linhas: DesenhaObjeto( ); // Desenha o objeto na posição nas // coordenadas originais glTranslatef(10,10,10); DesenhaObjeto( ); // Desenha o objeto deslocado de 10 // unidades em cada eixo

47. Transformação de Escala O comando que permite a mudança das dimensões de um modelo é glScale( TYPE x, TYPE y, TYPE z) e muda as escalas relativas a cada eixo principal;

48. O comando glScale é relativamente simples mas a utilização do fator de escala não-uniforme afetará os objetos desenhados;

49. Por exemplo, para triplicar a altura de um objeto usa-se: glScalef(1.0f,3.0f,1.0f);

50. Transformação de Rotação O comando para a rotação é glRotate(TYPE angle, TYPE x, TYPE y, TYPE z) e tem como parâmetro o ângulo de rotação e as coordenadas de um vetor que determina o eixo de rotação (ângulos de Euler).

51. Para a rotação ser feita em torno de um dos eixos principais, deve-se definir x, y e z apropriadamente como os vetores unitários nas direções destes eixos. Por exemplo, a rotação do ponto de visão de 30º em torno do eixo x pode ser definida como: glRotatef(30.0f,1.0f,0.0f,0.0f);

52. Referências CONCI , Aura ; Eduardo Azevedo ; LETA, F. R. . Computação Gráfica - Teoria e Prática - Vol. 2. Rio de Janeiro: Campus Elsevier, 2003.

53. http://pt.wikipedia.org/wiki/OpenGL.

54. http://www.inf.pucrs.br/~pinho/CG/Aulas/Vis2d/Instanciamento/Instanciamento.htm

55. http://www.dca.ufrn.br/~ambj/opengl/transformacoes.html