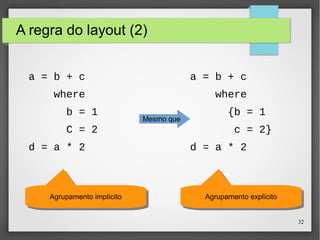
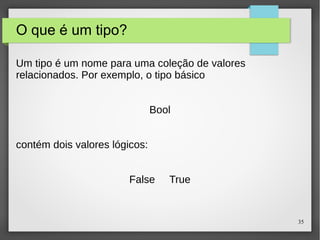
O documento discute o paradigma funcional de programação e linguagens funcionais. Ele apresenta os problemas da crise do software e como as linguagens funcionais podem ajudar a resolvê-los, permitindo programas mais claros, concisos e seguros. Em seguida, explica os conceitos-chave de programação funcional e fornece exemplos nas linguagens Haskell e Lisp.





![6
Exemplo
● Somando inteiros de 1 a 10 em Haskell:
sum [1..10]
● O método de computação é aplicação de função.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-6-320.jpg)





![12
Haskell - Exemplo
f [] = []
f (x:xs) = f ys ++ [x] ++ f zs
where
ys = [ a | a <- xs, a <= x ]
zs = [ b | b <- xs, b > x ]
?](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-12-320.jpg)


![17
Funções em listas
● Seleciona o primeiro elemento de uma lista:
> head [1,2,3,4,5]
1
● Remove o primeiro elemento de uma lista:
> tail [1,2,3,4,5]
[2,3,4,5]
● Seleciona o enésimo elemento de uma lista:
> [1,2,3,4,5] !! 2
3
● Seleciona os primeiros n elementos de uma lista:
> take 3 [1,2,3,4,5]
[1,2,3]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-17-320.jpg)
![18
Funções em listas (2)
● Remove os primeiros n elementos de uma lista:
> drop 3 [1,2,3,4,5]
[4,5]
● Calcula o comprimento de uma lista:
> length [1,2,3,4,5]
5
● Calcula a soma dos elementos de uma lista:
> sum [1,2,3,4,5]
15](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-18-320.jpg)
![19
Funções em listas (3)
● Calcula o produto dos elementos de uma lista:
> product [1,2,3,4,5]
120
● Junta duas listas:
> [1,2,3] ++ [4,5]
[1,2,3,4,5]
● Reverte uma lista:
> reverse [1,2,3,4,5]
[5,4,3,2,1]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-19-320.jpg)







![27
Meu primeiro script (3)
● Agora Prelude.hs e teste.hs estão carregados, e as
funções dos dois scripts podem ser usadas:
> quadruple 10
40
> take (double 2) [1,2,3,4,5,6]
[1,2,3,4]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-27-320.jpg)
![28
Meu primeiro script (4)
● Mantendo o Hugs aberto, retorne ao editor, adicione as
definições abaixo, salve e digite :reload no Hugs:
factorial n = product [1..n]
average ns = sum ns `div` length ns
● Nota:
–
● div é cercado por aspas invertidas (crase);
● x `f` y é apenas um syntactic sugar para f x y.
● div é cercado por aspas invertidas (crase);
● x `f` y é apenas um syntactic sugar para f x y.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-28-320.jpg)
![29
Meu primeiro script (5)
> factorial 10
3628800
> average [1,2,3,4,5]
[1,2,3]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-29-320.jpg)


![33
Exercícios
● 1. Teste os slides 17-19 e 25-29 usando Hugs;
● 2. Corrija os erros do programa abaixo, e teste sua
solução usando Hugs.
N = a 'div' lenght xs
where
a = 10
xs = [1,2,3,4,5]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-33-320.jpg)



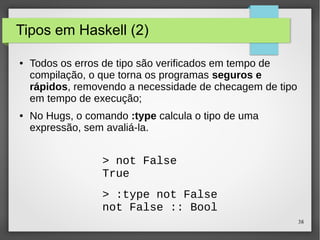

![40
Tipos Lista
● Uma lista é uma sequência de valores do mesmo tipo:
[False,True,False] :: [Bool]
['a','b','c','d'] :: [Char]
● De maneria geral:
[t] é o tipo de listas de elementos do tipo t.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-40-320.jpg)
![41
Tipos Lista (2)
● Nota:
– O tipo das listas não diz nada sobre o seu tamanho
[False,True] :: [Bool]
[False,True,False] :: [Bool]
– O tipo dos elementos não tem restrições. Por exemplo,
é possível criar listas de listas:
[['a'],['b','c']] :: [[Char]]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-41-320.jpg)

![43
Tipos Tupla (2)
● Nota:
– O tipo de uma tupla codifica seu tamanho:
(False,True) :: (Bool,Bool)
(False,True,False) :: (Bool,Bool,Bool)
– Não há restrições para o tipo dos componentes:
('a',(False,'b')) :: (Char,(Bool,Char))
(True,['a','b']) :: (Bool,[Char])](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-43-320.jpg)

![45
Tipos Função (2)
● Nota:
– A flecha → é digitada no teclado como ->;
– Não há restrições para o tipo de argumento e
resultados. Por exemplo, funções com múltiplos
argumentos ou resultados são possíveis usando listas
ou tuplas.
add :: (Int,Int) → Int
add (x,y) = x + y
zeroto :: Int → [Int]
zeroto n = [0..n]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-45-320.jpg)



![49
Por que Currying é útil?
● Funções curried são mais flexíveis que funções em tuplas,
porque funções úteis muitas vezes podem ser construídas
aplicando parcialmente uma função curried.
● Por exemplo:
add' 1 :: Int → Int
take 5 :: [Int] → [Int]
drop 5 :: [Int] → [Int]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-49-320.jpg)


![52
Funções Polimórficas
● Uma função é chamada polimórfica (“de muitas formas”)
se seu tipo contém uma ou mais variáveis de tipo.
length :: [a] → Int
Para qualquer tipo a, length toma uma lista
de valores do tipo a e retorna um inteiro.
Para qualquer tipo a, length toma uma lista
de valores do tipo a e retorna um inteiro.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-52-320.jpg)
![53
Funções Polimórficas (2)
● Nota:
– Variáveis de tipo podem ser instanciadas para
diferentes tipos em diferentes circunstâncias:
> length [False,True]
2
> length [1,2,3,4]
4
aa == BBooooll
aa == IInntt
– Variáveis de tipo devem começar com letras
minúsculas, e usualmente são nomeadas a, b, c, etc.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-53-320.jpg)
![54
Funções Polimórficas (3)
● Várias funções do prelude são polimórficas:
fst :: (a,b) → a
head :: [a] → a
take :: Int → [a] → [a]
zip :: [a] → [b] → [(a,b)]
id :: a → a](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-54-320.jpg)
![Char não é um
tipo numérico
55
Funções Polimórficas (4)
● Variáveis de tipo restrito podem ser instanciadas para
qualquer tipo que satisfaça a restrição.
> sum [1,2,3]
6
> sum [1.1,2.2,3.3]
6.6
> sum ['a','b','c']
ERROR
aa == IInntt
aa == FFllooaatt
Char não é um
tipo numérico](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-55-320.jpg)


![59
Exercícios
● Quais são os tipos dos seguintes valores?
['a','b','c']
('a','b','c')
[(False,'0'),(True,'1')]
[(False,True),('0','1')]
[tail,init,reverse]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-59-320.jpg)





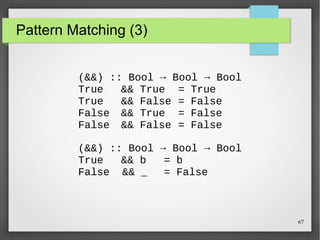

![69
Padrões de Listas
● Internamente, toda lista não-vazia é construída pelo uso
repetido do operador (:) chamado “cons” que adiciona
um elemento ao início da lista.
[1,2,3,4]
SSiiggnniiffiiccaa 11::((22::((33::((44::[[]]))))))](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-69-320.jpg)
![70
Padrões de Listas
● Funções em listas podem ser definidas utilizando padrões
x:xs.
head :: [a] → a
head (x:_) = x
tail :: [a] → [a]
tail (_:xs) :: xs
head e tail mapeia qualquer lista não-vazia para
head e tail mapeia qualquer lista não-vazia para
seus primeiros e últimos elementos
seus primeiros e últimos elementos](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-70-320.jpg)
![71
Padrões de Listas
● Nota:
– O padrão x:xs somente casa listas não-vazias:
> head []
Error
– Padrões x:xs devem ser parentesados, por que a
aplicação do padrão tem prioridade sobre (:). Por
exemplo, a seguinte definição retorna um erro:
head x:_ = x](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-71-320.jpg)








![80
Por que Lambdas são úteis?
Expressões lambda poder ser usadas para evitar dar nomes
a funções que são referenciadas uma vez apenas.
Por exemplo:
odds n = map f [0..n-1]
where
f x = x*2 + 1
Pode ser simplificado para
odds n = map (λx → x*2 + 1) [0..n-1]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-80-320.jpg)



![84
Exercícios
1.Considere a função safetail que tem o mesmo
comportamento da função tail, exceto por safetail mapear
lista vazia para lista vazia, sendo que tail retorna um erro
neste caso.
– Defina safetail usando:
● Uma expressão condicional;
● Uma expressão abrigada (guarded);
● Casamento de padrões.
– Dica: a função null :: [a] → Bool pode ser usada para
verificar se uma lista é vazia.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-84-320.jpg)

![87
Listas por Compreensão (2)
● Em Haskell, um notação por compreensão similar pode
ser usada para construir novas listas a partir de listas
antigas.
[x^2 | x ← [1..5]]
A lista [1,4,9,16,25] de todos os números x^2
tal que x seja um elemento da lista [1..5]
A lista [1,4,9,16,25] de todos os números x^2
tal que x seja um elemento da lista [1..5]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-87-320.jpg)
![88
Listas por Compreensão (3)
● Nota:
– A expressão x ← [1..5] é chamada geradora, pois ela
define como gerar os valores para x;
– Compreensões podem ter várias geradoras, separadas
por vírgula. Por exemplo:
> [(x,y) | x ← [1,2,3], y ← [4,5]]
[(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-88-320.jpg)
![89
Listas por Compreensão (4)
● Nota:
– Alterando a ordem das geradoras altera a ordem dos
elementos na lista final:
> [(x,y) | x ← [4,5], y ← [1,2,3]]
[(1,4),(2,4),(3,4),(1,5),(2,4),(3,5)]
– Múltiplas geradoras são como laços aninhados, sendo
as últimas geradoras são os laços mais profundos onde
os valores das variáveis se alteram com mais frequência.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-89-320.jpg)
![90
Listas por Compreensão (5)
● Por exemplo:
> [(x,y) | x ← [4,5], y ← [1,2,3]]
[(1,4),(2,4),(3,4),(1,5),(2,4),(3,5)]
x ← [1,2,3] é a última geradora, sendo assim
x ← [1,2,3] é a última geradora, sendo assim
o valor do componente x
se altera com mais frequência
o valor do componente x
se altera com mais frequência](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-90-320.jpg)
![91
Geradoras Dependentes
● As últimas expressões geradoras podem depender de
variáveis introduzidas nas primeiras geradoras.
[(x,y) | x ← [1..3], y ← [x..3]]
A lista [(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)]
de todos os pares dos números (x,y)
A lista [(1,1),(1,2),(1,3),(2,2),(2,3),(3,3)]
de todos os pares dos números (x,y)
tal que x,y sejam elementos da lista [1..3] e y >= x
tal que x,y sejam elementos da lista [1..3] e y >= x](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-91-320.jpg)
![92
Geradoras Dependentes
● Usando uma expressão geradora dependente pode-se
definir uma função de biblioteca que concatena uma lista
de listas.
concat :: [[a]] → [a]
concat xss = [x | xs ← xss, x ← xs]
● Por exemplo:
concat [[1,2,3],[4,5],[6]]
[1,2,3,4,5,6]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-92-320.jpg)
![93
Guards
● Listas por compreensão podem usar “guards” para
restringir o valor produzido pelas primeiras geradoras.
[x | x ← [1..10], even x]
A lista [2,4,6,8,10]
A lista [2,4,6,8,10]
de todos os números x tal que x seja
um elemento da lista [1..10] e x seja par
de todos os números x tal que x seja
um elemento da lista [1..10] e x seja par](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-93-320.jpg)
![[x | x <- [1..n], n `mod` x == 0]
94
Guards
● Usando “guards” é possível definir uma função que
mapeia um número inteiro positivo para sua lista de
fatores:
factors :: Int -> [Int]
factors n =
● Por exemplo:
> factors 15
[1,3,5,15]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-94-320.jpg)
![95
Guards
● Um inteiro positivo é primo se seus únicos fatores forem 1
e ele mesmo. Sendo assim, usando factors é possível
definir uma função que decide se um número é primo:
prime :: Int → Bool
prime n = factors n == [1,n]
● Por exemplo:
> prime 15
False
> prime 7
True](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-95-320.jpg)
![96
Guards
● Agora, usando “guards” é possível definir uma função que
retorna a lista de todos os primos até um dado limite:
primes ::Int → [Int]
primes n = [x | x ← [2..n], prime x]
● Por exemplo:
> primes 40
[2,3,5,7,11,13,17,19,23,29,31,37]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-96-320.jpg)
![97
A função Zip
● Uma função de biblioteca muito útil, qual mapeia duas
listas para uma lista de pares de seus elementos
correspondentes.
zip :: [a] → [b] → [(a,b)]
● Por exemplo:
> zip ['a','b','c'][1,2,3,4]
[('a',1),('b',2),('c',3)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-97-320.jpg)
![98
A função Zip
● Usando zip é possível definir uma função que retorna uma
lista de todos os pares de elementos adjacentes de outra
lista:
pairs :: [a] → [(a,a)]
pairs xs = zip xs (tail xs)
● Por exemplo:
> pairs [1,2,3,4]
[(1,2),(2,3),(3,4)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-98-320.jpg)
![● Usando pairs é possível definir uma função que decide se
os elementos de uma lista estão ordenados:
99
sorted :: Ord a => [a] → Bool
sorted xs =
and [x <= y | (x,y) ← pairs xs]
● Por exemplo:
> sorted [1,2,3,4]
True
> sorted [1,3,2,4]
False](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-99-320.jpg)
![● Usando zip é possível definir uma função que retorna uma
lista de todas as posições de um valor em uma lista:
100
positions :: Eq a => a → [a] → [Int]
positions x xs =
[i | (x',i) ← zip xs [0..n], x == x']
where n = length xs - 1
● Por exemplo:
> positions 0 [1,0,0,1,0,1,1,0]
[1,2,4,7]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-100-320.jpg)
![101
Compreensões em String
● Uma string é uma sequência de caracteres cercadas por
aspas duplas. Internamente, no entanto, strings são
representadas como listas de caracteres.
“abc” :: String
Significa Significa [['a'a',','b'b',','c'c']'] :::: [[CChhaarr]]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-101-320.jpg)
![102
● Similarmente, compreensões em strings podem ser
usadas para definir funções em strings como, por
exemplo, uma função que conta as letras minúsculas
(caixa-baixa) em uma string:
lowers :: String → Int
lowers xs =
length [x | x ← xs, isLower x]
● Por exemplo:
> lowers “Haskell”
6](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-102-320.jpg)
![103
Exercícios
1. Um tripla (x,y,z) de inteiros positivos é chamada de
pitagórica se x² + y² = z². Usando uma compreensão
em lista, defina a função
pyths :: Int → [(Int,Int,Int)]
que mapeia um inteiro n para todas as triplas com
componentes em [1..n]. Por exemplo:
> pyths 5
[(3,4,5),(4,3,5)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-103-320.jpg)
![104
Exercícios
2. Um inteiro positivo é perfeito se for igual à soma de
todos os seus fatores, excluindo o próprio número.
Usando uma compreensão de lista, defina uma
função
perfects :: Int → [Int]
que retorne a lista de todos os números perfeitos até um
dado limite. Por exemplo:
> perfects 500
[6,28,496]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-104-320.jpg)

![106
Funções recursivas
● Como visto, muitas funções podem ser definidas em
termos de outras funções.
factorial :: Int → Int
factorial n = product [1..n]
factorial mapeia qualquer inteiro n para o produto dos
factorial mapeia qualquer inteiro n para o produto dos
inteiros entre 1 e n
inteiros entre 1 e n](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-106-320.jpg)
![107
Funções recursivas (2)
● Expressões são avaliadas em um processo passo-a-passo
de aplicação de funções em seus argumentos.
● Por exemplo:
factorial 4
=
product [1..4]
=
product [1,2,3,4]
=
1*2*3*4
=
24](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-107-320.jpg)
![108
Funções recursivas (3)
product :: [Int] → Int
product [] = 1
product (x:xs) = x * product xs
....
fact 4 [1,2,3,4]
=
product (1:(2:(3:(4:[]))))
=
1 * product (2:(3:(4:[])))
.
.
.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-108-320.jpg)




![113
Recursões em listas
● Recursão não se restringe à números, mas também pode
ser usado para definir funções em listas.
product :: [Int] → Int
product [] = 1
product (x:xs) = x * product xs
product mapeia a lista vazia para 1, e qualquer outra
lista não-vazia para sua cabeça multiplicada pelo
product mapeia a lista vazia para 1, e qualquer outra
lista não-vazia para sua cabeça multiplicada pelo
produto de sua calda.
produto de sua calda.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-113-320.jpg)
![114
Recursões em listas (2)
product [2,3,4]
=
2 * product [3,4]
=
2 * (3 * product[4])
=
2 * (3 * ( * 4 * product[])
=
2 * (3 * (4 * 1))
=
24](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-114-320.jpg)
![115
Recursões em listas (3)
● Usando o mesmo padrão de recursão como em product
pode-se definir a função length em listas.
length :: [a] → Int
length [] = 0
length (_:xs) = 1 + length xs
length mapeia um lista vazia para 0, e qualquer outra
lista não-vazia para o sucessor do comprimento de
length mapeia um lista vazia para 0, e qualquer outra
lista não-vazia para o sucessor do comprimento de
sua calda.
sua calda.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-115-320.jpg)
![116
Recursões em listas (4)
length [1,2,3]
=
1 + length [2,3]
=
1 + (1 + length [3])
=
1 + (1 + (1 + (length []))
=
1 + (1 + (1 + (0))
=
3](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-116-320.jpg)
![117
Recursões em listas (5)
● Usando um padrão similar de recursão pode-se definir a
função reverse em listas.
reverse :: [a] → [a]
reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
reverse mapeia um lista vazia outra lista vazia, e
qualquer outra lista não-vazia para o reverso da sua
reverse mapeia um lista vazia outra lista vazia, e
qualquer outra lista não-vazia para o reverso da sua
calda concatenada com a cabeça.
calda concatenada com a cabeça.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-117-320.jpg)
![118
Recursões em listas (4)
reverse [1,2,3]
=
reverse [2,3] ++ [1]
=
(reverse [3] ++ [2]) ++ [1]
=
((reverse [] ++ [3] ++ [2]) ++ [1]
=
(([] ++ [3] ++ [2]) ++ [1]
=
[3,2,1]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-118-320.jpg)
![119
Múltiplos argumentos em recursão
● Funções com mais de um argumento também podem ser
definidas usando recursão.
● Por exemplo, zipping os elementos de duas listas:
zip :: [a] → [b] → [(a,b)]
zip [] _ = []
zip _ [] = []
zip (x:xs) (y:ys) = (x,y) : zip xs ys](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-119-320.jpg)
![120
Múltiplos argumentos em recursão (2)
● Remover os primeiros n elementos de uma lista:
drop :: Int → [a] → [a]
drop 0 xs = xs
drop (n+1) [] = []
drop (n+1) (_:xs) = drop n xs
● Concatenar duas listas:
(++) :: [a] → [a] → [a]
[] ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-120-320.jpg)

![122
Quicksort (2)
● Usando recursão, esta especificação pode ser traduzida
diretamente para uma implementação:
qsort :: [Int] -> [Int]
qsort [] = []
qsort (x:xs) =
qsort menores ++ [x] ++ qsort maiores
where
menores = [a | a <- xs, a <= x]
maiores = [b | b <- xs, b > x]
Nota:
Esta é provavelmente a implementação mais
simples de quicksort em qualquer linguagem de
programação.
Nota:
Esta é provavelmente a implementação mais
simples de quicksort em qualquer linguagem de
programação.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-122-320.jpg)
![123
Quicksort (3)
qq [[33,,22,,44,,11,,55]]
qq [[22,,11]] ++++ [[33]] ++++ qq [[44,,55]]
qq [[11]] ++++ [[22]] ++++ qq [[]] qq [[]] ++++ [[44]] ++++ qq [[55]]
[[11]] [[]] [[]] [[55]]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-123-320.jpg)
![124
Exercícios
● Sem olhar no prelude padrão, defina as seguinte biblioteca de funções usando
recursão:
– Verificar se todos os valores em uma lista são verdadeiros:
and :: [Bool] → Bool
– Concatenar uma lista de listas:
concat :: [[a]] → [a]
– Produzir uma lista com n elementos idênticos:
replicate :: Int → a → [a]
– Selecionar o iésimo elemento de uma lista:
(!!) :: [a] → Int → a
– Verificar se um valor é um elemento de da lista:
elem :: Eq a => a → [a] → Bool](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-124-320.jpg)



![128
A função map
● A função de alta ordem da biblioteca chamada map aplica
uma função para cada elemento de uma lista.
map :: (a → b) → [a] → [b]
● Por exemplo:
> map (+1) [1,3,5,7]
[2,4,6,8]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-128-320.jpg)
![129
A função map (2)
● A função map pode ser definida em uma maneira
particularmente simples usando compreensão de lista.
map f xs = [f x | x ← xs]
Alternativamente, para provar, a função map pode ser
definida utilizando recursão:
map f [] = []
map f (x:xs) = f x : map f xs](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-129-320.jpg)
![130
A função filter
● A função de alta ordem filter seleciona todos os
elementos de uma lista que satisfazem um predicado.
filter :: (a → Bool) → [a] → [a]
● Por exemplo:
> filter even [1..10]
[2,4,6,8,10]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-130-320.jpg)
![131
A função filter (2)
● Filter pode ser definida utilizando compreensão de lista.
filter p xs = [x | x ← xs, p x]
Alternativamente, pode ser definida utilizando recursão:
filter p [] = []
filter p (x:xs)
| p x = x : filter p xs
| otherwise = filter p xs](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-131-320.jpg)
![132
A função foldr
● Várias funções em listas podem ser definidas utilizando o
seguinte padrão simples:
f [] = v
f (x:xs) = x ⊕ f xs
f mapeia um lista vazia para algum valor v, e
qualquer outra lista não vazia para alguma uma
função ⊕ aplicada na cabeça e f na calda
f mapeia um lista vazia para algum valor v, e
qualquer outra lista não vazia para alguma uma
função ⊕ aplicada na cabeça e f na calda](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-132-320.jpg)
![133
A função foldr (2) - Exemplo
sum [] = 0
sum (x:xs) = x + sum xs v = 0
v = 0
⊕ = +
⊕ = +
product [] = 1
product (x:xs) = x * product xs
v = 1
⊕ = *
v = 1
⊕ = *
and [] = True
and (x:xs) = x && and xs
v = True
⊕ = &&
v = True
⊕ = &&](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-133-320.jpg)

![135
A função foldr (4)
● foldr pode ser definida usando recursão:
foldr :: (a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x:xs) = f x (foldr f v xs)
● No entanto, é melhor pensar em foldr de forma não
recursiva, simultaneamente substituindo cada (:) em uma
lista para um função dada, e [] para um valor dado.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-135-320.jpg)
![136
A função foldr (5)
sum [1,2,3]
=
foldr (+) 0 [1,2,3]
=
foldr (+) 0 (1:(2:(3:[])))
=
1+(2+(3+0))
=
6
Substitua cada (:)
por (+) e [] por 0
Substitua cada (:)
por (+) e [] por 0](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-136-320.jpg)
![137
A função foldr (6)
product [1,2,3]
=
foldr (*) 1 [1,2,3]
=
foldr (*) 1 (1:(2:(3:[])))
=
1*(2*(3*1))
=
6
Substitua cada (:)
por (*) e [] por 1
Substitua cada (:)
por (*) e [] por 1](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-137-320.jpg)
![138
A função foldr (7)
● Mesmo foldr encapsulando um padrão de recursão
simples, ela pode ser usada para definir muitas outras
funções do que se possa esperar.
● Relembrando a função length:
length :: [a] -> Int
length [] = 0
length (_:xs) = 1 + length xs](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-138-320.jpg)
![Substitua cada (:)
por λ_ n → 1+n e
139
A função foldr (8)
length [1,2,3]
=
length (1:(2:(3:[])))
=
1+(1+(1+0))
=
3
Substitua cada (:)
por λ_ n → 1+n e
[] por 0
[] por 0
length = foldr (_ n -> 1+n) 0](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-139-320.jpg)
![Reverse [] = []
reverse (x:xs) = reverse xs ++ [x]
Substitua cada (:)
por λx xs → xs ++
140
A função foldr (9)
reverse [1,2,3]
=
reverse (1:(2:(3:[])))
=
(([] ++ [3]) ++ [2]) ++ [1]
=
[3,2,1]
Substitua cada (:)
por λx xs → xs ++
[x] e [] por []
[x] e [] por []
● Agora relembrando a função reverse:](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-140-320.jpg)
![Substitua cada (:)
por (:) [] por ys
141
A função foldr (10)
● Portanto, nós temos:
(++ ys) = foldr (:) ys Substitua cada (:)
por (:) [] por ys
reverse =
foldr (x xs -> xs ++ [x]) []
● Finalmente, nota-se que a função de concatenação (++)
tem uma definição particularmente compacta utilizando
foldr:](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-141-320.jpg)


![144
Outras funções de biblioteca (2)
● A função de biblioteca all decide se todos os elementos de
uma lista satisfazem um dado predicado.
all :: (a -> Bool) -> [a] -> Bool
all p xs = and [p x | x <- xs]
● Por exemplo:
> all even [2,4,6,8,10]
True](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-144-320.jpg)
![145
Outras funções de biblioteca (3)
● Similarmente, a função de biblioteca any decide se pelo
menos um elemento de uma lista satisfaz um dado
predicado.
any :: (a -> Bool) -> [a] -> Bool
any p xs = or [p x | x <- xs]
● Por exemplo:
> any isSpace "abc def"
True](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-145-320.jpg)
![takeWhile :: (a -> Bool) -> [a] -> [a]
takeWhile p [] = []
takeWhile p (x:xs)
146
Outras funções de biblioteca (4)
● A função de biblioteca takeWhile seleciona elementos de
uma lista enquanto um predicado for verdadeiro.
| p x = x : takeWhile p xs
| otherwise = []
● Por exemplo:
> takeWhile isAlpha "abc def"
"abc"](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-146-320.jpg)
![dropWhile :: (a -> Bool) -> [a] -> [a]
dropWhile p [] = []
dropWhile p (x:xs)
147
Outras funções de biblioteca (5)
● A função de biblioteca takeWhile seleciona elementos de
uma lista enquanto um predicado for verdadeiro.
| p x = dropWhile p xs
| otherwise = x:xs
● Por exemplo:
> dropWhile isSpace " abc"
"abc"](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-147-320.jpg)
![148
Exercícios
● Expresse a compreensão [f x | x ← xs, p x] utilizando as
funções map e filter.
● Redefina map f e filter p usando foldr.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-148-320.jpg)

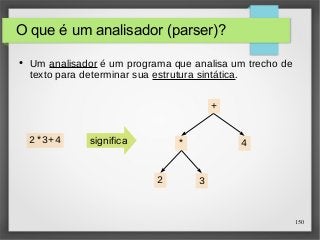


![153
O tipo Parser (2)
● No entanto, um analisador pode não requerer toda sua
string de entrada, sendo assim também é retornada a
entrada não utilizada.
type Parser = String -> (Tree,String)
● Uma string pode ser analisada de várias maneiras,
incluindo nenhuma, então generaliza-se para uma lista de
resultados:
type Parser = String -> [(Tree,String)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-153-320.jpg)
![154
O tipo Parser (3)
● Finalmente, um analisador nem sempre pode produzir
uma árvore, então generaliza-se para uma valor de
qualquer tipo:
type Parser = String -> [(a,String)]
Nota:
Para simplificar, esta sendo considerado somente
analisadores que ou falham e retornam um lista vazia
de resultados, ou têm sucesso e retornam uma lista
singleton (apenas um valor).
Nota:
Para simplificar, esta sendo considerado somente
analisadores que ou falham e retornam um lista vazia
de resultados, ou têm sucesso e retornam uma lista
singleton (apenas um valor).](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-154-320.jpg)
![155
Analisadores básicos
● O analisador item falha se a entrada é vazia, e consome o
primeiro caractere caso contrário:
item :: Parser Char
item = inp -> case inp of
[] -> []
(x:xs) -> [(x,xs)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-155-320.jpg)
![156
Analisadores básicos (2)
● O analisador failure sempre falha:
failure :: Parser a
failure = inp -> []
● O analisador return sempre tem sucesso, retornando o
valor v sem consumir nenhuma entrada:
return :: a -> Parser a
return v = inp -> [(v,inp)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-156-320.jpg)
![157
Analisadores básicos (2)
● O analisador p +++ q se comporta como o analisador p se
tiver sucesso, e como o analisador q caso contrário:
(+++) :: Parser a -> Parser a -> Parser a
p +++ q = inp -> case p inp of
[] -> parse q inp
[(v,out)] -> [(v,out)]
● A função parse aplica um analisador a uma string:
parse :: Parser a -> String -> [(a,String)]
parse p inp = p inp](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-157-320.jpg)
![158
Exemplos
● O comportamento dos cinco analisadores primitivos
podem ser ilustrados com exemplos simples:
% hugs parse.hs
> parse item “”
[]
> parse item “abc”
[('a',”bc”)]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-158-320.jpg)
![159
Exemplos (2)
> parse failure "abc"
[]
> parse (return 1) "abc"
[(1,"abc")]
> parse (item +++ return 'd') "abc"
[('a',"bc")]
> parse (failure +++ return 'd') "abc"
[('d',"abc")]](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-159-320.jpg)

![162
Sequenciamento (2)
● Se qualquer analisador em uma sequência de
analisadores falhar, então a sequência interia falhará. Por
exemplo:
> parse p "abcdef"
[(('a','c'), "def")]
> parse p "ab"
[]
● A notação do não é especificada no tipo Parser, mas pode
ser utilizada com qualquer tipo monadico.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-162-320.jpg)
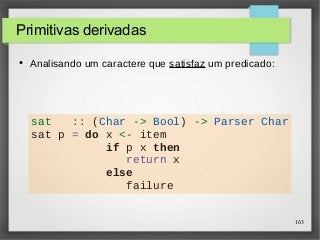
![164
Primitivas derivadas (2)
● Analisando um dígito e caracteres específicos:
digit :: Parser Char
digit = sat isDigit
char :: Char -> Parser Char
char x = sat (x ==)
● Aplicando um analisador zero ou mais vezes:
many :: Parser a -> Parser [a]
many p = many1 p +++ return []](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-164-320.jpg)
![165
Primitivas derivadas (3)
● Aplicando um analisador uma ou mais vezes:
many1 :: Parser a -> Parser []
many1 p = do v <- p
vs <- many p
return (v:vs)
● Analisando um string de caracteres específica:
string :: String -> Parser String
string [] = return []
string (x:xs) = do char x
string xs
return (x:xs)](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-165-320.jpg)
![166
Exemplo
● Agora é possível definir um analisador que consome um
lista de um ou mais dígitos de uma string:
p :: Parser String
p = do char '['
d <- digit
ds <- many (do char ','
digit)
char ']'
return (d:ds)](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-166-320.jpg)
![167
Exemplo (2)
● Agora é possível definir um analisador que consome um
lista de um ou mais dígitos de uma string:
> parse p "[1,2,3,4]"
[("1234","")]
> parse p "[1,2,3,4"
[]
Nota:
Bibliotecas de análise mais sofisticadas podem
indicar e/ou recuperar-se de erros na string de
entrada.
Nota:
Bibliotecas de análise mais sofisticadas podem
indicar e/ou recuperar-se de erros na string de
entrada.](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-167-320.jpg)












![183
getLine :: IO String
getLine = do x <- getChar
if x == 'n' then
return []
else
do xs <- getLine
return (x:xs)
Primitivas derivadas
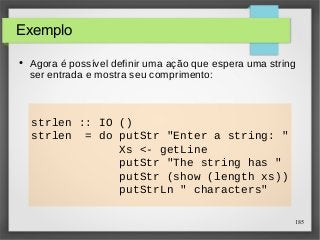
● Lendo uma string a partir do teclado:](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-183-320.jpg)
![184
putStr :: String -> IO ()
putStr [] = return ()
putStr (x:xs) = do putChar x
putStr xs
putStrLn :: String -> IO ()
putStrLn xs = do putStr xs
putChar 'n'
Primitivas derivadas(2)
● Escrevendo uma string na tela:
● Escrevendo uma string e movendo para uma nova linha:](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-184-320.jpg)



![189
sgetLine :: IO String
sgetLine = do x <- getCh
if x == 'n' then
do putChar x
return []
else
do putChar '-'
Xs <- sgetLine
return (x:xs)
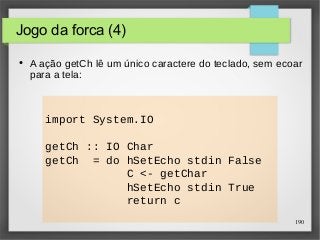
Jogo da forca (3)
● A ação sgetLine lê um linha de texto do teclado, ecoando
cada caractere como um traço -:](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-189-320.jpg)

![Jogo da forca (6)
● A função diff indica quais caracteres de uma string
ocorrem na segunda string:
[if elem x ys then x else '-' | x <- xs]
192
diff :: String -> String -> String
diff xs ys =
● Por exemplo:
> diff "haskell" "pascal"
"-as--ll"](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-192-320.jpg)
![Dica:
Represente o tabuleiro como
uma lista de cinco inteiros que
representam o número de
asteriscos remanescentes em
cada linha. Por exemplo, o
tabuleiro inicial é: [5,4,3,2,1].
193
1: * * * * *
2: * * * *
3: * * *
4: * *
5: *
Exercício
● Implemente o jogo nim em Haskell
– Regras:
● O tabuleiro é composto de 5 linhas
de asteriscos;
● Dois jogadores revesam a
remoção de um ou mais asteriscos
do fim de uma única linha;
● O ganhador é o jogador que
remover o último asterisco ou
asteriscos do tabuleiro. Dica:
Represente o tabuleiro como
uma lista de cinco inteiros que
representam o número de
asteriscos remanescentes em
cada linha. Por exemplo, o
tabuleiro inicial é: [5,4,3,2,1].](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-193-320.jpg)

![Declarações de tipo
● Em Haskell, um novo nome para um tipo existente pode
ser definido usando uma declaração de tipo.
type String = [Char]
String String éé uumm ssiinnôônniimmoo ddee ttiippoo [[CChhaarr]]..](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-195-320.jpg)


![Declarações de tipo (3)
● Declarações de tipo podem ser aninhadas:
type Pos = (Int,Int)
type Trans = Pos ->
Pos
● No entando, não podem ser recursivas:
type Tree = (Int,[Tree])](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-198-320.jpg)


![Declarações de dados (3)
● Valores de novos tipos podem ser usados da mesma
forma dos tipos nativos. Por exemplo, dado
data Answer = Yes | No | Unknown
● Pode-se definir:
answers :: [Answer]
answers = [Yes,No,Unknown]
flip :: Answer -> Answer
flip Yes = No
flip No = Yes
flip Unknown = Unknown](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-201-320.jpg)


![Declarações de dados (6)
● Sem surpresas, as próprias declarações de dados podem
conter parâmetros. Por exemplo, dado
data Maybe a = Nothing | Just a
● Pode-se definir:
safediv :: Int -> Int -> Maybe Int
safediv _ 0 = Nothing
safediv m n = Just (m `div` n)
safehead :: [a] -> Maybe a
safehead [] = Nothing
safehead xs = Just (head xs)](https://image.slidesharecdn.com/paradigma-funcional-131118220116-phpapp01/85/Paradigma-funcional-204-320.jpg)
