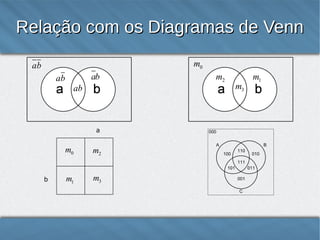
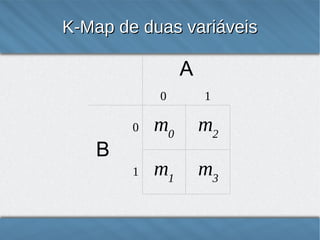
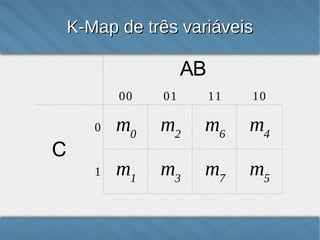
O documento introduz os Mapas de Karnaugh, uma técnica para simplificar expressões lógicas através da representação gráfica das variáveis e termos em um mapa. Os mapas organizam as combinações lógicas de variáveis em células adjacentes de acordo com o código de Gray para facilitar a identificação de termos comuns. Exemplos demonstram como construir e usar mapas de Karnaugh para expressões de 2, 3 e 4 variáveis.

1. Introdução aos Mapas de
Karnaugh
Prof. Tony Alexander Hild
Lógica Digital – 1 CC – Unicentro – 2013

2. O que são Mapas de Karnaugh?
●
Ou Mapas de Veitch-Karnaugh, ou K-Maps:
–
●
●
Forma alternativa de simplificar circuitos lógicos;
Ao invés de usar técnicas de simplificação da álgebra booleana, pode-se transferir valores
lógicos de uma expressão Booleana ou uma tabela-verdade para um mapa de Karnaugh:
–
●
●
Criado por Edward Veitch (1952) e aperfeiçoado pelo engenheiro de telecomunicações Maurice
Karnaugh.
Usando mintermos ou maxtermos.
O arranjo de 0s e 1s dentro do mapa ajuda a visualizar as relações lógicas entre as
variáveis e leva diretamente a uma expressão Booleana simplificada;
Usado para expressões com até 5 variáveis independentes:
–
Comumente utilizado para simplificar expressões com até 4 variáveis;
–
Mais do que 5 variáveis torna difícil identificar as células adjacentes, sendo melhor utilizar métodos
computacionais.
2

3. Relação com os Diagramas de Venn
m0
ab
ab
ab
m2
ab
m3
m1
a
m0
b
m2
m1
m3
3

4. Definições
Células = 2n , onde n é o número de
variáveis
Por exemplo: uma expressão com duas variáveis formará um mapa com
22=4 células
A
B
0
1
A
B
0
0
A+ B A + B
0
00
1
A+ B A + B
1
01
Maxtermo
A
1
0
1
10
11
B
2
3
0
1
0
1
AB
A B AB
AB
Mintermo
4

5. Montagem
●
Células adjacentes devem diferir em apenas um bit:
–
Código de Gray.
Dec
0
1
2
3
4
5
6
7
Gray
000
001
011
010
110
111
101
100
Binário
000
001
010
011
100
101
110
111
5

6. K-Map de duas variáveis
A
0
1
0
m0
m2
1
m1
m3
B
6

7. K-Map de três variáveis
AB
00
01
11
10
0
m0
m2
m6
m4
1
m1
m3
m7
m5
C
7

8. K-Map de quatro variáveis
AB
00
01
11
10
00
m0
m4
m12
m8
01
m1
m5
m13
m9
11
m3
m7
m15 m11
10
m2
m6
m14 m10
CD
8

9. Exemplos
●
Duas variáveis:
–
0
S=A+B
1
2
3
A
0
0
1
1
B
0
1
0
1
A
A
0
0
B
1
S
0
1
1
1
1
m0
m2
m1
m3
0
1
0
0
1
1
1
1
B
9

10. Exemplos
●
Três variáveis:
–
0
1
S = ABC
2
3
4
5
6
7
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
AB
AB
00
0
C
1
S
0
0
0
0
0
0
0
1
01
11
10
m0
m2
m6
m4
m1
m3
m7
m5
00
01
11
10
0
0
0
0
0
1
0
0
1
0
C
10

11. Exemplos
●
Quatro variáveis:
–
0
S = AB+CD
1
2
3
4
5
6
AB
AB
00
01
11
10
00
m0
m4
m12
m8
01
m1
m5
m13
m9
11
m3
m7
m15 m11
10
m2
m6
m14 m10
CD
7
00
01
11
10
00
0
0
1
0
01
0
0
1
0
CD
11
1
1
1
1
10
0
0
1
0
8
9
10
11
12
13
14
15
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
S
0
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
11