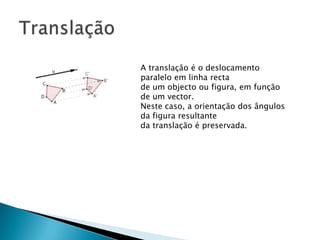
1) O documento discute diferentes tipos de isometrias do plano, que são transformações geométricas que preservam distâncias. 2) As quatro principais isometrias são reflexões, translações, rotações e reflexões deslizantes. 3) O texto fornece instruções detalhadas para construir exemplos de cada uma dessas isometrias geometricamente usando um software.

2. A maneira mais conveniente de definir um
conceito geral de congruência, para além do
conceito de congruência de segmentos, de
ângulos ou de triângulos, é através do conceito
de isometria do plano. Etimologicamente o
termo “isometria” significa “mesma medida”.
(Adaptado de Transformações Geométricas, A.
F. Oliveira)

3. Uma isometria ou movimento rígido é uma aplicação de
um conjunto de pontos num
conjunto de pontos que preserva as distâncias, isto é, a
distância entre dois quaisquer pontos
é a mesma entre os seus transformados.
Em geral, e quando não houver possibilidade de
confusão, designam-se por A’, B’, C’, as
imagens dos pontos A, B, C, ... por uma isometria.
Toda a isometria do plano euclidiano é de um dos quatro
tipos: reflexões (ou simetrias axiais), translações, rotações
ou reflexões deslizantes.

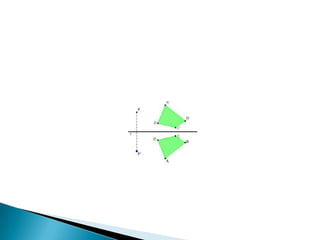
4. Dada uma recta r, a reflexão é uma transformação que
deixa invariante qualquer ponto da recta e que
transforma cada ponto (P) exterior à recta noutro ponto
(P´) no lado oposto da recta relativamente a P, de tal
modo que a recta r é mediatriz do segmento de recta
[PP´]. A recta r é o eixo de simetria da reflexão, por
vezes também denominada de “espelho”.
Note-se que a orientação dos ângulos da figura
reflectida é invertida.

6. 1. Construa uma recta, um ponto que não lhe pertença
e um polígono.
2. A recta constitui o eixo de simetria, pelo que vamos
construir o ponto simétrico e o
polígono simétrico, relativamente à recta. Para o fazer
terá de seleccionar o modo
Reflexão em relação a uma recta no 7º botão da barra
de ferramentas.
3. Seleccione depois o objecto que pretende reflectir e
posteriormente o eixo de simetria.
Deste modo fará surgir os objectos reflectidos. Se
alterar os objectos originais poderá
observar de imediato o efeito da simetria axial sobre os
novos objectos.

7. A translação é o deslocamento
paralelo em linha recta
de um objecto ou figura, em função
de um vector.
Neste caso, a orientação dos ângulos
da figura resultante
da translação é preservada.

8. 1. Construa um polígono, e um segmento de recta
orientado, representante de um vector.
Para construir o vector deve seleccionar o modo Vector definido
por dois pontos no 3º botão da barra de ferramentas. Coloque o
cursor num local da vista geométrica e pressione o botão
esquerdo do rato para marcar o ponto origem. Afaste e
faça o mesmo noutro local para marcar o ponto extremidade e
obter o vector.
2. De seguida seleccione o modo Translação por um vector no 7º
botão da barra de ferramentas para efectuar a translação do
polígono segundo o vector. Seleccione com o rato o polígono e
de seguida o vector, o que fará construir a translação do
polígono. Se alterar o vector, a partir de um dos pontos que o
define ou o polígono original poderá
observar de imediato muitos exemplos.

9. A composição de duas reflexões, cujos eixos são as
rectas concorrentes s e r, é uma Rotação com centro
no ponto de intersecção de s e r e de amplitude igual
ao dobro da amplitude do ângulo entre s e r. A dupla
inversão dos ângulos corresponde à preservação da
orientação entre a figura inicial e a final, pelo que é
também preservada a orientação dos ângulos nas
figuras resultantes de uma rotação.

10. Para efetuar uma rotação de um polígono dado o
centro da rotação e a amplitude do
ângulo de rotação proceda do seguinte modo:
1. construa um ponto (centro da rotação) e um
polígono (a sofrer uma rotação com centro
no ponto e segundo determinada amplitude);
2. de seguida selecione o modo Rodar em torno de um
ponto com uma amplitude no 7º botão da barra de
ferramentas. Selecione com o rato o polígono e de
seguida o ponto, o que fará construir o polígono
rodado segundo um Ângulo cuja amplitude terá de
inscrever numa janela que surgir (tem a opção de
rodar no sentido horário ou anti-horário. Se mudar
de local o centro da rotação ou alterar o polígono
original observará de imediato muitos exemplos.

11. A composição de uma reflexão numa recta com uma translação ao longo dessa
recta é uma reflexão deslizante.
A recta em questão é chamada eixo da reflexão deslizante. Neste caso, a
orientação dos ângulos é invertida de figura para figura.
Construa um polígono e efectue uma reflexão deslizante ao longo de uma recta.