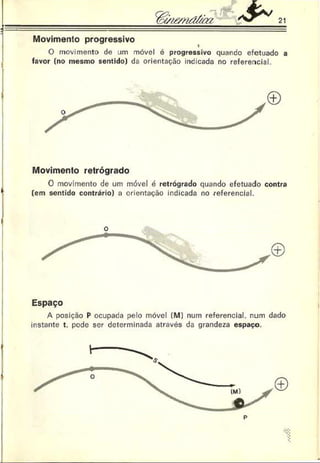
A coleção consiste em oito volumes sobre diferentes tópicos da física, como mecânica, óptica e eletromagnetismo. Cada capítulo apresenta introdução teórica, questões resolvidas e propostas. O documento introduz conceitos básicos da mecânica como referencial, movimento, repouso, trajetória, espaço, intervalo de tempo e deslocamento escalar.

2. A coleção consta de
oito volumes:
/Mecânica: Cinemática
Mecânica: Dinâmica
^M ecânica: Estática, Hidrostática e Gravitação
Óptica Geométrica
r
O Termologia
6 Oscilações, Ondas e Acústica
/^Eletricidade: Eletrodinàmica
(3 Eletricidade: Eletrostática e Eletromagnetismo
Cada capítulo apresenta as
seguintes partes:
0. Introdução Teórica
ti. Questões Resolvidas
C Questões Propostas
d. Respostas

5. CfflïU
LO
1

6. s
A Física é o ramo da Ciência que, juntamente
com a Matemática, a Biologia e a Química,
procura explicar os fenômenos que ocorrem na
Natureza, tais como os movimentos dos corpos, as
trocas de energia entre sistemas, a
propagação da luz, etc.
Introdução à Mecânica
• Mecânica — Para melhor analisar esses fenômenos, a Física é
dividida em partes. A Mecânica é a parte da Física que estuda os
movimentos dos corpos, bem como suas causas e conseqüências.
Por sua vez, a Mecânica está subdividida em Cinemática. Dinâmica,
Estática, Hidrostática e Gravitação.

8. 10
(1571-1630)
Matemático e astrónomo alemão.
Estabeleceu as leis cinemáticas do
movimento dos planetas ao redor
do Sol. Criou as bases para o
futuro desenvolvimento da Mecânica.
(1564-1642)
Matemático o astrônomo italiano.
Estabeleceu as leis do movimento dos
projéteis e a Lei da Inércia.
Introduziu o método científico na
observação dos fenômenos e
contribuiu decisivamente para o
desenvolvimento da Mecânica.
Fisico e astrónomo inglês Fez a
síntese das idéias de Kepler e
Galileo. estabelecendo as Leis da
Dmâmica e a Lei ca Gravitação
Universal. Seus trabalhos modificaram
a visão humana do Universo.

9. Unidade
Fundamentalmente. a solução de um problema de Física consiste
em determinar as grandezas nele envolvidas. Medir uma grandeza
é compará-la com outra de mesma espécie denominada unidade.
Ouandc a unidade puder ser representada materialmente, teremos
o padrão.
Sistemas de unidades mecânicas
Para medirmos as grandezas mecânicas, necessitamos de um
conjunto de unidades denominado sistema de unidades mecânicas,
definido pelas unidades das grandezas fundamentais: comprimento,
massa ou força e tempo.
• Sistema Internacional (SI) — No Brasil, a partir de 1963, foi ado­
tado o Sistema Internacional (SI), cujas unidades mecânicas funda­
mentais estão representadas no quadro:
Grandeza Unidade Símbolo
comprimento metro m
massa quilograma kg
tempo segundo s
Devido às iniciais dos símbolos, este sistema de unidades também é
conhecido como MKS.

10. 12
• Sistema CGS — Com unidade® derivada» do Sistoma Interna*
cional, podemos construir outro sistema de unidades mecânicas, o
CGS. cujas unidades estão representadas no quadro:
Grandeza Unidade Símbolo
comprimento centímetro cm
massa grama g
tempo segundo s
• Sistema Técnico — É tradicionalmente utilizado em áreas téc­
nicas Suas unidades fundamentais são apresentadas no quadro:
Grandeza Unidade Símbolo
comprimento metro m
força quilograma-furça kgf
tempo segundo s
Usualmente adotam-se, ainda, as unidades quilômetro (compri­
mento) e hora (tempo), onde:
1 km = 1 000 m
e
1 h = 3 600 s
Intensidade de uma grandeza
O resultado da comparação entre uma grandeza e a unidade é
um número real (positivo ou nulo) denominado valor numérico da
grandeza em relação àquela unidade.
O conjunto formado pelo valor numérico e pela unidade é deno
minado intensidade da grandeza.
Exemplo:

11. ( //////////#>/
-
Ao modlrmON u nlturo do um homom, obtemos 1.70 m.
Nosto cflHo, tomos:
grandeza medida: comprimento (altura):
unidade: metro (m);
valor numérico: 1.70;
intensidade da grandeza: 1,70 m.
Assim, medir uma grandeza é, na realidade, determinar sua in­
tensidade
Ponto material
Quando as dimensões do objeto a ser analisado não interferem
na solução do problema, dizemos que ele é um ponto material.
Um automóvel em viagem numa estrada pode ser considerado como um
ponto material.
Assim, um móvel em translação pode ser estudado como um
ponto material.
Introdução à Cinemática
Movimento de translação de uma carga.

12. 14
Na translação de um corpo, o comportamento de todos os seus
pontos c o mesmo. Basta, então, estudar o comportamento de um
único ponto (ponto material).
Resumindo:
Translação ■►o corpo pode ser considerado ponto material.
Durante uma rotação, as dimensões do objeto interferem na so­
lução co problema. Neste caso, não podemos considerá-lo como ponto
material.
Na rotação de um corpo, cada ponto possui comportamento dis­
tinto dos demais, não podendo ser encarado como ponto material.
Resumindo:
Rotação ■►o corpo não pede ser considerado ponto material.
Observe que a Terra, juntamente com os demais planetas, pode
ser considerada como ponto matéria em relação ao seu movimento
de translação ao redor do Sol.

13. 15
Porém, em relação ao movimento de rotação, em torno do seu
próprio eixo. ela não pode ser considerada como ponto material.
ê$J& r/ac& 2.__________________________________ __________
Embora as dimensões do corpo estudado como ponto material não
sejam consideradas, sua massa deverá ser levada em conta quando
necessário.
Referencial
Os movimentos de um móvel devem ser analisados em relação
a um sistema de referência, também denominado referencial.
O referencial está. em geral, associado a um outro corpo. Assim,
por exemplo, o movimento do passageiro de um carro pode ser estu­
dado em relação ao “ referencial-carro" ou em relação ao “ referencial-
-Terra
Dependendo do problema analisado, os referenciais tomados
poderão ser uni. bi ou tridimensionais.

14. 16
rrp • Aplicações
Referencial unidimensional: a localização de um móvel é feita
através de um único número: Xp (coordenada).
Movimento de um corro numa estrada.
Referencial bidimensional: a localização do móvel é feita através
dc dois números: Xp e Yp(coordenadas).
Referencial tridimensional: a localização do móvel P é feita através
de três números: Xpf Y p e Zy (coordenadas).
Vôo de um pássaro num viveiro.

15. 17
Movimento
Dizemos que um ponto materiai está em movimento em relação
a um referencial quando sua posição se alterar ao longo do tempo
neste referencial. Isso significa que, no mínimo, uma de suas co­
ordenadas varia com o tempo.
Mudança de posiçíío: movimento.
Aplicação
Um passageiro sentado está em movimento,
juntamente com seu veiculo, em relação à Terra
Repouso
Dizemos que um ponto material está em repouso, em relação
a um referencial, quando sua posição não se alterar ao longo do
tempo, neste referencial. Ou seja. quando suas coordenadas neste
referencial não sc alterarem com o tempo.
Posição inalterada: repouso.

16. 18
i* Aplicações
1. Observe que um móvel pode se encontrar em repouso em relação
a um referencial e em movimento em relação a outro.
Na figura abaixo:
• a caixa está em repouso em relação ao caminhão, pois sua po­
sição não varia em relação a ele (referencial B).
• a caixa está em movimento em relação à estrada, pois sua posi­
ção varia em relação a ela (referencial A).
Indica 3xposiçõo da caix3
em relação ao caminhão.
a posição
em
à
estrada.
2. Na figura abaixo representamos a posição de um poste em relação
a um carro. Se a posição do poste varia em relação ao carro, di­
zemos que o poste movimenta-se em relação ao carro.
V ® ®
Conclusão Movimento e repouso são conceitos relativos, depen­
dendo do referencial adotado. Ao descrevermos um movimento, é
conveniente adotarmos um sistema de referência onde a descrição do
fenômeno torne-se a mais simples possível.

17. & 19
Trajetória «
Denomina-se trajetória de um móvel a sucessão de posições
ocupadas por ele cm re ação ao referencial adotado.
Os sulcos deixados pelo veículo na areia indicam a trajetória do móvel.
trens percorrem uma trajetória previamente traçada.
A trajetória dos aviões a .ato pode ser observada através da fumaça que
se origina da condensação do vapor dos gases liberados.

18. Geralmente, a trajetória é representada por uma função mate­
mática e sempre depende do referencial adotado.
Exemplo:
C .
Desprezando as influências do ar, a trajetória de uma bomba, que
cai de um avião em vôo horizontal com rapidez constante, será um
arco ce parábola em relação ao solo e um segmento de reta vertical
cm relação ao avião.
A orientação da trajetória e a escolha de uma origem sobre ela
facilitam a análise do movimento, pois permitem a associação de
sinais a algumas grandezas que o caracterizam.
Orientação da trajetória c escolha da origem (O)
Esquema simplificado:

19. Movimento progressivo
«
O movimento de um móvel é progressivo quando efetuado a
favor (no mesmo sentido) da orientação indicada no referencial.
©
Movimento retrógrado
0 movimento de um móvel é retrógrado quando efetuado contra
(em sentido contrário) a orientação indicada no referencial.
©
Espaço
A posição P ocupada pelo móvel (M) num referencial, num dado
instante t. pode ser determinada através da grandeza espaço.
p

20. e#>
c/*/
22
0 espaço S é a medida algébrica do arco de trajetória que tem
início na origem do referencial e extremidade na posição ocupada
pelo móvel.
Ou seja: S = OP.
No Sistema Internacional, o espaço é medido em metros: no Sis­
tema CGS, em centímetros, e, no Sistema Técnico, em metros.

21. toî/zemdJim
Aplicações práticas
Marco quilométrico nas estradas:
Numeração das casas numa rua:

22. 24
ü fó & va flfà L___________________________________________________
J. Ccnliecendo-se o espaço de um móvel não se tem Icéia se ele *vai
“vem", ou simplesmente está em repouso. Se o móvel está no
quilômetro 30. não significa que ele tenha andado 30 km.
i
2. Observe a figura seguinte Nela representamos um referencial associado
à própria estrada, onde se desenvolvem os movimentos dos móveis
A. B C e D. Orientando-se este referencial, teremos as regiões positiva
e negativa.
Podemos, então, escrever: móvel A: SA ——30 km:
móvel B: S „= + 2 0 k m ; móvel C (observador):
Sc = 0 .<
m (origem): móvel D: SD = 0km (origem).
Para a mesma posição, três situações diferentes: o móvel A “vai", o móvel
B ‘ vem’ e o observador C está em repouso.
L

23. Simpliíicadamente teremos:
í
I
Intervalo de tempo
Entre o início e o fim da análise de um movimento decorre um
intervalo de tempo At definido como a diferença ent-e o instante
final e o instante inicial
11. é sempre maior que tin: então, At será sempro positivo.
Um fenómeno f r 0 fenômeno
físico tem seu W r * seu término
início quando o quando o
cronômetro . i — ! cronômetro
registra 5 s. registra 15 s.
Logo: v Logo:
*»n = 5 S instante finai — tfh. = 15 s
à r
Duração do fenômeno
i ‘ s
Intérvalo de
tompo At *"
/ I I v
At = tf,„ - t(ll = 15s —5 s Logo |A
> -0 s|

24. 26
Deslocamento escalar
Deslocamento escalar AS de um móvel num dado intervalo de
tempo é a diferença entre o espaço final e o espaço inicial das
posições que ele ocupa nos extremos deste intervalo.
Ou seja: AS — Srm— Sir,
Deslocamento escalar: AS = S,
Esquema simplificado: s .
Vejamos, agora, qual a interpretação física que devemos dar para
os sinais do deslocamento escalar.
1) Se, por exemplo, no instante 4 s um móvel ocupa a posição inicial
determinada por Si„ — 10 m e num instante 12 s ele ocupa a po­
sição final determinada por Sn« —30 m. seu deslocamento escalar
será:
à
I
I
Intervalo de tempo
Deslocamento escalar
A' —tfi„—tj,,
At = 12s 4 s —8 s
AS = Sflll S|M
AS 30 m — 10 m = +20 m

25. ^ Conclusão: Durante o intervalo de tempo de 8 s, o móvel teve um
^ des ocamento escalar de +20 m. ,
O sinal “ mais” significa que, se o móvel manteve sempre o mes­
mo sentido de percurso, seu movimento desenvolveu-se a favor
do sentido do referencial unidimensional adotado.
Assim, nos movimentos progressivos, o deslocamento escalar é
positivo.
2) Se no instante 15 s o móvel ocupa a posição inicial determinada
por $i;, = 35m e no instante 25 s ele ocupa a posição final deter­
minada por Sun — 20 m. seu deslocamento escalar será:
AS = Sm, — Si„ = 20 m — 35 m => AS = —15 m
s n„ - 20 m
Intervalo dc tempo A
* tfin —*
iii
At = 25s — 15s = 10 s
Deslocamento escalar
AS = SflI(- S iu
AS = 20 m —35m = 15 m
Conclusão: Durante o intervalo de tempo de 10 s. o móvel teve um
deslocamento escalar de —15 m.
O sinal "menos" significa que, se o móvel manteve sempre o mes­
mo sentido de percurso, seu movimento desenvolveu-se contra o
sentido do referencial unidimensional adotado.
Assim, nos movimentos retrógrados, o deslocamento escalar é
negativo.
Movimentos progressivos - ► AS > 0
Movimentos retrógrados AS < 0

26. Ouando o móvel retorna ao ponto de partida ou permanece em repouso,
o deslocamento escalar é nulo.
posição
inicial
Distância percorrida
A distância percorrida por um móvel é a soma dos módulos dos
deslocamentos escalares realizados por ele durante seu movimento,
acrescida da unidade correspondente.
Assim, por exemplo, a distância percorrida por um automóvel
corresponde à quilometragem feita por ele durante uma viagem.
Resumindo:
d = |ASi| + |AS»| + . . . + |ASn|
Exemplo:
Para um móvel que parte da posição A, atinge B e retorna, che­
gando ao ponto C, teremos:
1) AS = So — S a = 0m — 10m —10m
2) d — AB + BC = 10m + 20m = 30 m

27. O « inholo , S dovo anr entendido como módulo da grandeza AS e
corroapondo ao valor rtumórico da grandeza AS rjue ó um número real
positivo ou nulo.
Exemplo:
AS n -2 m- ► AS| =4-2
Velocidade escalar
Velocidade é a grandeza física que permite medir a rapidez com
que um móvel varia sua posição.
• Velocidade escalar média — Define-se velocidade escalar média
de um móvel como o quociente do deslocamento escalar pelo intervalo
de tempo correspondente.
Como o intervalo de tempo At é sempre positivo a velocidade
escalar media V„, terá o mesmo sinai do deslocamento escalar AS.
Ou seja: Vn
J =
At tfin tin
©

28. 30
• Velocidade escalar instantânea — Ouando o intervale de tempo
At tende a zero. a velocidade escalar média tende à velocidade escalar
instantânea.
Ou seja:
Posições sucessivas do um móvel entre dois instantes muito próximos.
velocidade média do
móvel entre dois instantes
muito próximos
velocidade
instantânea
• Unidades de velocidade
No Sistema Internacional, a velocidade é medida em m/s; no Sis­
tema CGS, em cm/s; no Sistema Técnico, em m/s. e, usualmente,
mede-se também a velocidade em km/h.
Aplicações práticas
Velocidade escalar média: guarda rodoviário controlando o limite
de velocidade de um veículo através de binóculo e cronômetro.

29. 31
• Sinais da velocidade escalar — Nos movimentos progressivos a
velocidade escalar instantânea é sempre positiva.
Nos movimentos retrógrados a velocidade escalar instantânea é
Ouando a velocidade de um móvel é instantaneamente nula, dize­
mos que ele está parado naquele instante.
Isto ocorre, por exemplo, no ponto mais alto do lançamento ver­
tical de uma pedra.
áà v = o
"" No instante em
que atinge o
ponto mais alto da
J sua trajetória, o
| móvel pára Porém,
não permanece
nessa posição com
V. V = 0.

30. í
Quando a velocidade escalar instantânea de um móvel perma­
nece nula durante um intervalo de tempe At, dizemos que ele está
em repouso naquele intervalo.
i Complementos
• A intensidade da velocidade escalar instantânea pode ser regis­
trada num instrumento denominado tacómetro (velocímetro).
O velocímetro do automóvel registra a intensidade tía velocidade escalar instartãrea
(rapidez do movimento).
• Algumas velocidades significativas:
Velocidade da luz no vácuo ............................................... 300 000 km/s
Velocidade do som no ar à temperatura de 20“ C .. 344 m/s
Velocidade média de translação da Terra ao redor
do Sol .................................................................................... 30 km/s
Importante: A velocidade é grandeza que depende do referencial ado­
tado. Assim, uma pessoa dormindo em sua casa possui velocidade
nula em relação à Terra, mas está dotada de velocidade não-nula em
relação ao Sol.
-
»
I
C
t*

31. 33
Aceleração escalar
Aceleração é o grandeza física que permite medir a rapidez com
que um móvel varia suei velocidade.
• Aceleração escalar média — Num intervalo de tempo M. um
móvel var a sua velocidade escalar de V.n a Vfln.
©
km. h
r 7 s
V
©
'
km.h
Define-se aceleração escalar média do móvel como o quociente
da variação de sua velocidade escalar pelo intervalo de tempo cor­
respondente.
Ou seja:
O sinal da velocidade
só indica o sentido
do movimento.
V,0 - 4C km/h Vf,u 4 85 krn-h
No exemplo:
85 40 45
= ------------= -----
30 - 15 15

32. 34
• Aceleração escalar instantânea — Quando o intervalo de tempo
At tende a zero, a aceleração escalar média tende à aceleração escalar
instantânea. At —o
Ou seja: a =
=lim a
.-„
a:-» ü
• Unidades de aceleração
AV
Lembrando que a,u= -----, então podemos concluir que:
At
unidade de
unidade de velocidade
aceleração unidade de
tempo
Assim, no Sistema Internacional teremos:
unidade de
velocidade
unidade de
tempo
No Sistema
unidade de
velocidade
unidade de
tempo
No Sistema
unidade de
velocidade
unidade de
tempo
km/h
Uma unidade usual é
s

33. Aplicação prática
Análise do desempenho de um automóvel: a velocidade de um
Corcel GT varia de 0 a 100 km/h num intèrvalo de tempo de 17,15 s:
a velocidade de um Passat TS varia de 0 a 100 km/h num intervalo
de tempo de 15,30s. (Dados extraídos ca revista Quatro Rodas de
junho de 1979.)
• Sinais da aceleração escalar — Analisemos o movimento de um
veículo onde, em cada um dos casos abaixo, o motorista procura
manter a leitura no velocímetro ou permanentemente crescente ou
permanentemente decrescente. Lembre-se de que o velocímetro só
registra as intensidades das velocidades; os sinais serão dispostos
de acordo com o sentido do movimento do móvel.
1} As velocidades do veículo crescem algebricamente:
Instante t«„ - 5s tf n- 10s
Velocidade Vj,, ——5 m/s Vf| „ - 4-15 m/s
A velocidade final é algebricamente maior que a velocidade n ciai.
1 5 - 5
a... -
1 0 - 5
a,, - + 2 m/s*
I
Velocidade Vh: — 15 m/s
A velocidade ^
está
crescendo
algebricamente-.
a ( I ). Instante
A ve ocidade final é algebricamente maior que a velocidade inicia!.
= —
(-15)
10 5
a„ - - 2 m/s
O sinal da velocidade só indica o sentido do movimento

34. Conclusão: A aceleração escalar do móvel é positiva sempre que
-- sua velocidade escalar crescer algebricamente.
2) As velocidades do veículo decrescem algebricamente:
A velocidade está
decrescendo
algebricamente: a ( )
Instante ti» - 5 s tr.„ = 10 s
Velocidade V,., - +15 m/s v n. “ +5 m/s
A velocidade final é algebricamente menor que a velocidade inicial.
5 - 1 5
aai = —
2m/s-
Instante t,» “ 5 s Win — 10 s
Velocidade V;1
I - - 5 m/s Vr.i. ™ -15 m/s
A velocidade final 6 algebricamente menor que a velocidade inicial.
-15 - ( - 5 )
am— a„ = —
2m/s-
O sinal da veiocidade só indica o sentido do movimento.
Conclusão: A aceleração escalar do móvel é negativa sempre
que sua velocidade escalar decrescer algebricamente.

35. %//M /n ã/àn 37
Movimentos acelerado e retardado
Quando a intensidade da velocidade escalar de um móvel cresce
num intervalo de tempo, o movimento é denominado acelerado.
Movimento acelerado
A velocidade aumenta em intensidade.
Corresponde á situação em que as leituras do velocímetro
assumem valores crescentes.
Quando a intensidade da velocidade escalar de um móvel decresce
num intervalo de tempo, o movimento é denominado retardado.
Movimento retardado
A velocidade diminui em intensidade.
Corresponde à situação em que as leituras do veloe metro
assumem valores decrescentes.
Resumo geral — Observe, nas duas pranchas a seguir, que o
sinal da aceleração de um móvel nada tem a ver com o fato de seu
movimento ser acelerado ou retardado. Assim, o fato de a aceleração

36. 38
ser positiva não implica necessariamente que o movimento seja ace­
lerado. bem como o fato de a aceleração ser negativa não implica
necessariamente que o movimento seja retardado.
MOVIMENTO ACELERADO
Cálculo tía aceleração
Entre Os e 5 s:
km/h
Entre 5 s e 10 s:
8 0 - 6 0 km/h
$ 1 0 - 5 s
ACELERAÇÃO POSITIVA
VELOCIDADE POSITIVA
MOVIMENTO ACELERADO
MOVIMENTO ACELERADO
Cálculo da aceleração
Entre Os e 5 s:
- 6 0 - (-40)
a —-----------------
5 - 0
ACELERAÇÃO NEGATIVA
VELOCIDADE NEGATIVA
Entre 5 s e 10 s :.
30 - (—60)
a ------------------
1 0 - 5
MOVIMENTO ACELERADO
O sinal da velocidade só indica o sentido do movimento.
Movimento acelerado: velocidade c aceleração tém o IVESMO SINAL!

37. f
Cálculo da aceleração
Entre 0 s e 5s
60 80
a —------ -—
3 - 0
l km/h
Entre 5 s e 10 s:
40 - 60 km/h
s 10- 5 s
ACELERAÇÃO NEGATIVA
VELOCIDADE POSITIVA MOVIMENTO RETARDADO
MOVIMENTO RETARDADO
Cálculo da aceleração
Entre 0 s e 5 s:
-60 - (-80)
a ------------------
5 - 0
km/h
a .. T-4------ -
Entre 5 s e 1Cs:
-40 - (-60) km/h
s 10- 5 s
ACELERAÇAO POSITIVA
VELOCIDADE NEGATIVA MOVIMENTO RETARDADO
O sinal da velocidade só indica o ser*, do do movimento
Movimento retardado: velocidade e aceleração têm SINAIS OPOSTOS!

38. 40
Portanto:
Movimento acelerado
Velocidade e aceleração têm o mesmo sinal.
- v . a > 0
Movimento retardado
Velocidade e aceleração têm sinais opostos.
- V . a < 0
Representação gráfica
A variação de uma grandeza em
visualizada através ce um diagrama.
função do temoo pode ser
Assim, o comportamento das ondas cerebrais de um homem pode
ser estudado através de um eletroencefalograma: um tremor de terra
pode ser analisado através de seu registro num sismógrafo.

39. 'W
ft
Analogamente, podemos analisar as variações do espaçe S. da
velocidade V e da aceleração a através de seus diagramas horários
S X t . V X t e a X t .
A leitura direta de um diagrama horário informa-nos sobre o com­
portamento da grandeza ern estudo ao longo do tempo.
Exemplo:
Da leitura direta do gráfico V X t abaixo, podemos concluir que:
• De Os a 5 s . V > 0 (movimento progressivo) e V cresce (movi­
mento acelerado).
• De 5 s a 10s, V > 0 (movimento progressivo) e V decresce
(movimento retardado).
• De 10 s a 15 s, V < 0 (movimento retrógrado) e jV| cresce (mo­
vimento acelerado).
• De 15 s a 20 s. V < 0 (movimento retrógrado) e V decresce
(movimento retardado).

40. 42
'fln
Gin
G
y<x
! AG
i
~A At 1
/ a ; i
i
/ "■
*fln t
Elementos gráficos
Além da leitura direta, há dois outros elementos de interesse
no estudo de um diagrama horário: o declive da curva e a área sob
o gráfico.
• Declive de uma curva * —
Dado um diagrama horário de
uma grandeza G (S. V ou a), cha­
mamos de declive do gráfico a
tangente trigonométrica do ân­
gulo formado pelo gráfico e o
eixo horizontal, medido no sen­
tido anti-horário a partir do eixo
t. Ou seja: | dec = tgõ~ .
Gráfico retilíneo: dec = tg a =
AG _ Gfln — G|n
At trtn —tln
Gráfico curvilíneo:
• declive médio
deCm — dec^j^p.^ tg &
• declive num ponto
deci» = tg a
Sinais do declive:
• para 0o< a < 90°, dec > 0.
Exemplo:
6 — 3
dec (o»m j»)-----------— “M ,5 —>
2 - 0
dec«)» mi‘») — 4-1.5
• para 90° < a < 180°, dec < 0.
Exemplo:
dec. s-h 7») =
0 - 6
7 - 5
= - 3 = >
dec <5. W7•! = —3
• Para a = 0 dec = 0.
Exemplo:
6 - 6
dec (2«H5•) = 0
_________ 5 — 2
j dec<
2■
h »»i — 0
* Pera maior facllidace. ver Apêndice (Pranchas Matemática») no linal deste livro

41. Admite-se que a escala de representação da grandeza G e da grandeza t
seja a mesma. f
Exemplo:
eixo da grandeza G (ordenada): 1cm representa 1m/s;
eixo da grandeza t (abscissa): 1cm representa 1s._________________________
• Área sob o gráfico — Mui­
tas vezes a área entre o gráfico
e o eixo dos tempos é numerica­
mente igual a uma certa gran­
deza física G, ou seja, A *?G .
Por outro lado, em muitos
casos, o sinal desta grandeza
está associado ao fato de o grá­
fico estar acima ou abaixo do
eixo dos tempos. Podemos, en­
tão. adotar a seguinte conven­
ção:
• área calculada acima do eixo
dos tempos: G > 0;
• área calculada abaixo do
eixo dos tempos: G < 0.
Exemplos:
8 + 4
D A IO» H 2 «) . 2 —
= 12 — >Ato» h 2») = 12
A ;2«m *h) — 2 . 8 = 16 =
—>A(2«h i >
0= 16
2 . 8
A h «h 6») =•--------= 8 :
==>A « «MA») — 8
Portanto, A(0, h 6*j = 12 +
■
+- 16-h 8 = 36
Sendo A 5 G, vem: |G = -f36
4 .8
2) A(«. mio») 16
Sendo A ^G. vem: | G = —16

42. 1. CESCEA — Um homem, ao inclinar-se sobre a janela do vagão
de um trem que .se move com velocidade constante, deixa cair
seu relógio. A trajetória do relógio, vista pelo homem do trem.
é (despreze a resistência do ar):
a) uma reta.
b) uma parábola.
c) um quarto de circunferência.
d) uma hipérbole.
e) Nenhuma das anteriores.
Resolução: Embora caia verticalmente, aproximando-se do chão, hori-
zontalmcntc o relógio acompanha o trem, devido ao seu embalo inicial.
Assim, em relação a uni referencial fixo no trem, a trajetória do objeto
será um segmento de reta vertical.
O mesmo ocorre quando um avião, voando horizontalmente com velo­
cidade constante, abandona um objeto que cai livre da resistência do ar.
— O ----
Resposta: alternativa a.

43. 45
2. CESCEA — Na questão anterior, a trajetória vista por uma pessoa
no solo é:
a) uma reta.
b) uma parábola. f
c) uma hipérbole.
d) um quarto de circunferência.
e) Nenhuma das anteriores.
Resolução: Fm relação a uni referencial fixo no solo, o relógio será
dotado de dois movimentos simultâneos: queda vertical e deslocamento
lateral. A combinação desses movimentos resulta em um arco de pará­
bola, conforme você pode observar no exemplo do avião.
Resposta: alternativa b.
3. ITA — Um homem sobe uma escada que se apóia contra um edi­
fício. A escada tem seu topo a 8 m do solo e a base está a 6 m
do edifício, conforme figura abaixo. Ele sobe ao topo em 4 s e.
daí, cai ao ponto B no próximo segundo. A velocidade escalar
média entre A e B é de:
Cv a) 3.2 m/s.
b) 1.2 m/s.
c) 3,6 m/s.
d) 5.25 m/s.
Bl_______________- N .a e) Nenhuma das respostas anteriores.
Resolução: Do enunciado da questão, temos:
CB = 8 m, AB = 6m , AtA
C= 4 s e Atou = 1 s
C
Por Pitágoras, podemos escrever:
(AB)2 + (CB)2= (AC)2
(6)2 -4- (8)2t= (AC)2
(AC)2 = 1 0 0 = > AC = 10 m
Lembrando a definição dc velocidade escalar média, vem:
.. AS AC + CB 10-f-8 18
" 6
■ât AtA
C-j- AtfB 4 -f- 1 5
Logo: Vrn= 3,6m /s
Resposta: alternativa c.

44. 46
4. MACKENZIE — Sejam M e N dois pontos de uma reta e P o ponto
médio de MN. Um homem percorre MP com veloc dade constante
de 4,0 m/s e PN com velocidade constante de 6,0 m/s. A velo­
cidade média do homem entre M e N é de:
a) 4,8 m/s.
b) 5,0 m/s.
c) 5.2 m/s.
d) 4.6 m/s.
e) Nenhuma das anteriores.
Resolução: Quando um móvel mantém sua velocidade constante, as
velocidades media e instantânea tem o mesmo valor.
y © g © a
At, At,
Ou seja:
velocidade
constante
V = V,
Assim, para o trecho MH podemos escrever:
AS, AS
Vm, = 4 m/s = > --------- = 4 = > At, = ------
* At, 4
Para o trecho PN, teremos:
AS2
Vrn = 6 m/ s = > ---------= 6 =>
Ata
A velocidade media total será:
ASp AS, -{- ASa
V — —
At? At, -}- Ato
Ata
ASa
6
(UI)
Substituindo-sc
AS,
AS,
(I) e (II) em (III), vem:
-I- AS. _ AS, + AS*
ASo ~ 3AS, + 2ASa
(D
(II)
12(AS, + AS-.)
3AS, -f- 2ASo
4 6 12

45. 47
Pelo enunciado, sendo P o ponto niédio do trecho MN, então MP — PN
ou AS, - AS,.
Portanto:
12(AS, + AS,) 2 4 # ,
~~ '
V«
24
3AS, -f 2AS,
Conclusão:
4,8
VmT — 4,8 m/s
Resposta: alternativa a.
5. MAPOFEI — Um automóvel percorre a distância entre São Paulo
e São José des Campos (90 km) com a velocidade média de
60 km/h; a distância entre São José dos Campos e Cruzeiro
(100 km) é percorrida com a velocidade média de 100 km/h e entre
Cruzeiro e Rio de Janeiro (210 km) com a velocidade média de
60 km/h. Calcule a velocidade média do automóvel entre São
Paulo e Rio de Janeiro.
Resolução: Para o trecho (1) (São Paulo—São José dos Campos):
AS, AS, 90
Vm = ------ = > At, = -----— = > A t, = ------= 5
1 At, V». 60
At, = 1,5 h
Para o trecho (2) (São José dos Campos—Cruzeiro):
AS2 AS2 100
V„, = ----i = > Ata = ---- — => At. = ---------= >
Ato 100
Ato = 1,0 h
Para o trecho (3) (Cruzeiro—Rio de Janeiro):
AS» AS3 4 210
At3 —---------—^ At:, —
V« = -
1 At: 60
At:, = 3,5 h
Assim, o intervalo de tempo total para ir de São Paulo ao Rio de
Janeiro será: _________
At = At, 4 Ato 4- At:, = 1,5 4- 1,0 4 3,5 = > At = 6,0 h

46. 48
O deslocamento total do automóvel será:
áS = AS, 4 AS. 4 AS3= 90 4 100 4 210 =>
Portanto:
AS = 400 km
V,
400
6
Vm— 66,6" km/h
Resposta: A velocidade média do automóvel em todo o trecho foi de
66,67 km/h.
6. CESGRANRIO — Numa avenida longa, os sinais são sincronizados
de tal forma que os carros, trafegando a uma determinada velo­
cidade, encontram sempre os sinais abertos (onda verde). Sa­
bendo que a distância entre sinais sucessivos (cruzamentos) é
de 200 m e que o intervalo de tempo entre a abertura de um sinal
e o seguinte c de 12 s. com que velocidade os carros devem
trafegar para encontrarem os sinais abertos?
a) 30 km/h
b) 40 km/h
c) 60 km/h
d) 80 km/h
e) 100 km/h
Resolução: Suponhamos que um carro esteja chegando num sinal
vermelho.
Quando o sinal abrir, ele terá 12 s para percorrer 200 m até o próximo
sinal, que deverá estar passando do vermelho para o verde.
At
Calculemos, então, com que velocidade média o carro deverá fazer
este percurso.
Sendo AS = 200 m c At = 12 s, vem:
AS 200 50
V ... —
— ■
■■ ■ v m=
50
At 12 3
Lembrando que I m/s = 3,6 km/h, ternos:
50
m/s
V,„ = . 3,6 km/h V
'n
-, = 60 km/h
Resposta: alternativa c.

47. 49
% /s/£ m d /ü r/ '
7. UNIVERSIDADE DE TAUBATé — Uma bicicleta move-se sobre
uma estrada curvilínea com velocidade escalar instantânea igual
a —4 rn./s. O sinal negativo indica que:
a) a bicicleta tem velocidade decrescente.
b) a bicicleta se move em marcpa a ré.
c) o movimento tem sentido contrário ao da orientação positiva
da trajetória.
d) é impossível tal situação; não há significado físico para velo­
cidade negativa.
Resolução: A velocidade escalar negativa indica que o objeto se move
contra a orientação do referencial.
Assim, diremos que o movimento da bicicleta é retrógrado.
)
Resposta: alternativa c.
8. UNIVERSIDADE DA BAHIA — O maquinista aciona os freios de
um trem, reduzindo sua velocidade de 80 km/h para 6C km/h, no
intervalo de 1 min. Neste intervale, a aceleração do trem foi de:
a) 20 km/h-’.
b) —20 km/h2.
c) —0.3 km/h2.
d) 1.2 . 103km/h-.
e) —1.2 . 103km/h2.
Resolução: Lembrando que a„,
AV Vfla — V|n
At At
podemos es-
crcver:
&
B
) —
Logo:
3iu — —
60 km/h — 80 km/h
1min
20 km/h km/h
1 min
a» = -2 0
mm

48. 50
Ou seja, o trem reduz sua velocidade, cm média, de 20km/h em cada
minuto.
Como 1min = ------h, entào:
60
am= -2 0 . 60 km — => am= —1 200 km/h2
h
Assim:
a,3 : 1.2 . 103km/h2|
O sinal menos (—) significa que a velocidade escalar do móvel diminui
algebricamente.
Resposta: alternativa e.
9. MEDICIMA DE LONDRINA — A tabela abaixo dá a velocidade es­
calar (V) de um corpo em função do tempo (t):
t(s) 0 2 4 6 8
V(cm's) -3 4 1
1 18 25
A pa-tir destes dados, assinale o gráfico que melhor representa
am«
o*ih 2(| = ---------------- — H
--------- — -f-3,5 cm/ s
2 - 0 2
B in <2 « H <*1 = ------------------ = H------------— - j- 3 , 5 c m / s - '
4 - 2 2
|-------= -f 3,5 cm/s*
. 2
a.-ii<
4aH 6sl —
6 - 4

49. 51
3m(uHM8*) — ---------------- — H
--------- — +3,5 cm/s2
8 - 6 2
Portanto, a aceleração media é constante c sua representação gráfica
é uma reta paralela ao eixo dos tempos (eixo horizontal).
Resposta: alternativa a.
10. ITA — No estudo do movimento de um móvel (em trajetória reti­
línea), medindo-se a velocidade a cada segundo a partir de um
instante t — 0 s e de um ponto x0 ob:eve-se a seguinte tabela:
V(m/s) 1.0 2.0 6.0 8.0 9.0 10.0 12.0 13.0 14.0 15.0 15,0 15.0 14.0 10,0 5.0 2.0
t(s) 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 80 9.0 10.0 110 12.0 130 14,0 15.0
As acelerações médias do móvel entre es instantes 4 s h 5 s ,
10s m 11s e 13 s m 14 s foram, respectivamente (em m/s2):
a) 1.0: 0.0 e 4.0.
b) 4.0; 0,5 e -4 .0 .
c) 2.0; 2.0 e -2 .0 .
d) 2.0; 0.0 e -4 ,0 .
e) 1.0; 0.0 e —4.0.
n . . » ^ fin ^ :n
Resolução: Como am—--------------- , temos:
tíin — tin
(4,0»H’»
.O*) —
1 0 ,0 -9 ,0
5,0 - 4,0
am(4«HG«) — 1,0 m/S-
am:10.0&
H 11,0-
a
»—
15,0 — 15,0
1,0
1,0
0,0
— 1,0 m/s2
3.H113.01 H14,0s) —
11,0 -1 0,0 1,0
am(to «HM«) = 0,0 m/s*
6,0— 10,0 -4 ,0
= 0,0 m/s*
14,0— 13,0 *1,0
— —4,0 m/s*
amíl3sHHj) — —4,0 m/s*
Resposta: alternativa c.
11. MEDICINA DE SANTOS — Um ponto material desloca-sc com uma
certa velocidade segundo um eixo orientado, adquirindo, na ori­
gem deste, uma aceleração constante de —15 cm/s2. Após 6,0 s
sua velocidade é de 30 cm/s, dirigida segundo o sentido negativo
do eixo. A velocidade do ponto material no instante cm que lhe
foi comunicada a aceleração é de:

50. 52
a) 15 cm/s.
b) 30 cm/s.
c) 45 cm/s.
d) 60 cm/s.
e) Nenhuma das anteriores.
Resolução: Do enunciado, temos a informação:
Vfu = —30 cm /s (velocidade contrária à orientação do referencial).
VfIn— V,0
Lembrando que aw
t = 0,0s V,„ = ?
t = 6,0s
'fii>
At
•©
■©
vem:
-1 5
-3 0 - V,
- 9 0 = -3 0 - V,B
= > Vla = 9 0 - 3 0 =>
Viu = 00 cm/s
Resposta: alternativa d.
12. FEI — O gráfico da velocidade de um ponto material em função
do tempo é o que se vê na figura abaixo. Pode-se dizer que:
a) o movimento é acelerado durante todo o tempo.
b) o movimento é retardado nos trechos AB, CD e DE.
c) o movimento só é retardado no trecho AB.
d) o movimento é retardado nos trechos AB e CD.
e) nenhuma das afirmações anteriores está correta.

51. 53
Resolução: As grandezas físicas escalares podem ter suas variações
com o tempo ilustradas através de uma representação gráfica. A leitura
de um gráfico nos permite tirar conclusões a respeito do movimento
do móvel.
No caso cm questão, o gráfico V X t nos informa que:
Trecho AB: V| decresce = > movimento c retardado.
Trecho BC: velocidade se mantem constante.
Trecho CD: V| decresce = > movimento c retardado.
Trecho DE: V cresce => movimento é acelerado.
Resposta: alternativa d.
13. MEDICINA DA SANTA CASA — O gráfico abaixo representa o
espaço S de um móvel em função do tempo t. Pode-se dizer que
a velocidade média no intervalo de Os a 7 s foi igual a:
c) 23 m/s.
d) 6,6 m/s.
e) 0 m/s.
«j, __^
Resolução: Lembrando que Vm—-------------, através da leitura direta
t f In t jn
do diagrama horário S X t podemos concluir que S()— 0 m e S7= 0 m.
Portanto:
Va
i(0 *
H7 s
)
Sv- So
7 - 0
0 - 0 0
------- = ------= 0 =>
7 7
—
^ ^a
i:o
*h T
«
>—0 m
; S
Observe que o fato dc a velocidade média ser nula não implica que o
móvel esteja cm repouso. No caso em questão, a velocidade média é
nula porque o móvel ocupa a mesma posição nos instantes inicial e final.
Resposta: alternativa e.

52. 54
14. MEDICINA DO ABC — O gráfico abaixo representa a velocidade
escalar em função do tempo de um veículo que se movimenta
sobre uma trajetória retilínea.
O módulo da aceleração escalar média, no intervalo de 0 s a 10.0 s.
b) 2.0.
c) 2.5.
d) 5.0.
e) 10.0.
Resolução: Lendo o gráfico, concluímos que:
para t = 0,0 s, Vrt — 20 m/s
para t = I0,0s, V10= Om/s
c . AV V|0 — V„
benao a*. = ------= ---------------- , vem:
At At
0 — 20
âjiMOHHio*.)----------------. . am
(o,sH»'»*) ——2,0 m/s*
1 0 - 0
A velocidade final é aleebricamcnte menor que a velocidade inicial.
Logo, em m/s2:
Resposta: alternativa b.
<
<f s H 10 *1
- 2.0

53. 55
1. MEDICINA DE 1TAJUBÁ — Um menino parado numa estação deixa
cair uma pedra. Um observador, situado num trem que se desloca com
movimento retilíneo para a esquerda, vê a pedra seguindo qual das traje­
tórias abaixo?
2. FUNDAÇÃO CARLOS CHAGAS — lodo movimento é relativo. Então,
podc-sc dizer que, cm relação a um mesmo sistema de referência:
I) Sc A está em movimento em relação a B e B está em movimento em
relação a C, então A está em movimento em relação a C.
II) Se A está parado em relação a B c B está parado em relação a C, então
A está parado em relação a C.
Responder mediante o seguinte código:
a) I está certa e II está errada.
b) I está errada e II está certa. d) I e II estão erradas.
c) I c II estão corretas. c) Nada se pode afirmar.
3. MEDICINA DO ABC — A velocidade escalar média de um móvel é me­
lhor definida como sendo:
a) a média das velocidades escalares do móvel, ao longo do movimento.
b) o resultado da divisão do espaço percorrido pelo móvel pelo intervalo
de tempo empregado em percorrer esse espaço.
c) o produto da aceleração pelo tempo.
d) o quociente da aceleração pelo tempo.
c) a media aritmética das velocidades inicial c final, relativas ao mesmo
percurso.

54. 56
4. ENGENHARIA DF. UBERLÂNDIA — Um passageiro dc ônibus verifi­
cou que o mesmo andou 10 km nos 10 primeiros minutos de observação c
8 km nos 10 minutos seguintes. A velocidade média do ônibus foi:
a) pouco menor que 60 km/h.
b) igual a 60 km/h.
c) pouco maior que 60 km/h.
d) igual a 120 km/h.
c) impossível dc ser calculada.
5. PUC (CAMPINAS) Lm carro move-se com velocidade de 2 m/s durante
10s (l.a marcha): cm seguida, com 5 m/s durante 10 s (2.a marcha) e, de­
pois, com II m/s durante 10s (3.a marcha). Desprcza-se a duração das
mudanças de marcha.
a) A velocidade média do carro c dc 6 m/s.
b) A aceleração do carro é sempre nula.
c) A aceleração media do carro na duração do fenômeno é de 0,45 m/s-.
d) Nenhum dos resultados anteriores.
6. MEDICINA DF. CATANDUVA — Um automóvel percorre um trecho
retilíneo dc estrada, indoda cidade A ate a cidade B,distante 150 km da
primeira. Saindo às 10:00 h dcA.pára às ll:00h emumrestaurante situa­
do no ponto médio do trecho AB, onde o motorista gasta exatamente uma
hora para almoçar. A seguir, prossegue viagem e gasta mais uma hora
para chegar à cidade B. A velocidade media do automóvel no trecho AB
foi dc:
a) 75 km/h. d) 60 km/h.
b) 50 km/h. c) 90 km/h.
c) 150 km/h.
7. ITA — Um motorista deseja perfa?er a distância de 20 km com a veloci­
dade média de 80 km/h. Se viajar durante os primeiros 15 minutos com a
velocidade de 40 km/h, com que velocidade média deverá fazer o percurso
restante?
a) 120 km/h.
b) 160 km/h.
c) É impossível estabelecer a velocidade mcd:a desejada nas circunstâncias
apresentadas.
d) Nula.
e) Nenhuma das afirmações c correta.
8. UNESP — Um ônibus dirige-sc dc São Paulo ao Rio dc Janeiro.
0) Ao passar pelo marco quilométrico A dc espaço 150 km, um passa­
geiro lê cm seu relógio o tempo 15 horas. Com esses dados, a veloci­
dade é calculada cm 10 km/h.
(2) Às 17 horas, o veículo passa por um marco B no qual se lê 50 km.
Entro A e B o percurso é —100 km. a duração é dc 2 horas e a velo­
cidade média é dc —50 km/h.
*
4
k
*
‘4

55. (3) O sinal negativo na velocidade do item (2), suposto correto, indica que
o veículo faz marcha à ré.
a) Somente (1) c correta.
b) Somente (2) é correta.
c) Somente (3) c correta.
d) Há mais de uma afirmativa correta.
e) Não há nenhuma afirmativa correta.
9. UNIVERSIDADE DE SÂO CARLOS — Um móvel se desloca de um
ponto A até um ponte B. a uma velocidade constante igual a 80,0 km/h.
Depois, se desloca do ponto B ate um ponto C, a uma velocidade constante
igual a 30,0 km/h. Se a trajetória é retilínea desde o ponto A até o ponto
C. c as distâncias de A até B c de B até C são iguais, podemos dizer que
a velocidade escalar média do móvel é de:
a) 55,0 km/h. d) 50,2 km/h
b) 43,6 km/h. e) 71.7 km/h.
c) 60.8 km/h.
10. PUC (RIO GRANDE DO SUL) — A velocidade média de um automóvel
na primeira metade de um determinado percurso é de 10 km/h c. na se­
gunda metade desse mesmo percurso, é de 30 km/h. Pode-se afirmar que
a velocidade média desse automóvel cm todo o percurso vale:
a) 15 km/h. d) 30 km/h.
b) 20 km/h. e) 40 km/h.
c) 25 km/h.
11. ENGENHARIA DE UBERLÂNDIA — Um ponto material move-se em
linha reta. percorrendo dois trechos consecutivos MN c NP O trecho MN
c percorrido com uma velocidade media igual a 20 km/h, e o trecho NP
com uma velocidade média igual a 60 km/h. O trecho NP é o dobro do
trecho MN. Pode-se afirmar que a velocidade média no trecho MP foi de:
a) 36 km/h. d) 42 km/h.
b) 40 km/h. e) Nenhuma das respostas anteriores.
c) 37,3 km/h.
12. MEDICINA DE ITAJUBÁ Um trem viaja durante 2h a 50,0 km/h;
depois, passa a viajar a 60,0 km/h durante 1,5 h e, finalmcntc. passa a
80,0 km/h durante 0,5 h. Sua velocidade média, neste trajeto, será de:
a) 80.0km/h. d) 57,5 km/h.
c) 63,3 km/h.
13. MEDICINA DE SANTOS — Um móvel, descrevendo um movimento pro­
gressivo, certamcnte está em:
b) 65,0 km/h. e) 47,5 km/h.
a) rotação.
b) oscilação.
c) movimento retilíneo.
d) movimento uniforme.
e) Nenhuma das respostas anteriores.

56. 58
14. FUNDAÇÃO CARLOS CHAGAS — Medindo-se, no sistema CGS dc
unidades, a velocidade de um corpo, obteve-se o vaíor de 12,3 cm/s. Que
valor expressa esta mesma velocidade no sistema de unidades MKS?
a) 1,23 . 10-3m/s d) 1,23 . 10*m/s
b) 1,23 . 10-* m/s e) 1,23 . IO3m/s
c) 1,23 . 10-» m/s
15. PUC (CAMPINAS) — A aceleração escalar média de um automóvel que
aumenta sua velocidade de 36 km/h para 108 km/h em 10s c de:
a) 7,2 m/s2. d) 4,2 m/s2.
b) 72 m/s2. e) 3,0 m/s2.
c) 2,0 m/s2.
16. UNIVERSIDADE DE SÄO CARLOS Um carro, movendo-se no sen­
tido positivo do eixo x com velocidade de 100 km/h. freia de modo que
após 1.0 min sua velocidade passa a ser dc 40 km/h. A aceleração média
do carro será dc:
a) —1,0 km/min2. d) —
0,66 km/min2.
b) 1.0 km/min2. c) 0.66 km/s2.
c) 1,0 m/s2.
17. FUNDAÇÃO CARLOS CHAGAS — O quociente entre velocidade c ace­
leração c uma grandeza que pode ser medida em:
a) cm/s2. d) s.
b) cm/s3. e) s-1.
c) cm2/s3.
18. FUNDAÇÃO CARLOS CHAGAS — O gráfico abaixo representa o espaço
S de um ponto em função do tempo t de percurso. A maior velocidade
média, relativa a um intervalo de tempo igual a um segundo, é obtida
entre:
•
I
a) 0 s e Is.
b) I s e 2 s.
c) 3 s e 4 s.
d) 4 s e 5 s.
e) 5 s e 6 s.

57. 59
v i& n d á a z &
19. MEDICINA DE TAUBATÉ O gráfico S X t de um móvel c desenhado
abaixo. Esse móvel tem um movimento:
t
a) aederado. d) retrógrado.
b) retardado. e) ü móvel está parado.
c) progressivo.
20. MEDICINA DE SANTOS O diagrama abaixo representa a velocidade
escalar de um ponto material em função do tempo.
Podemos afirmar que:
a) entre os instantes 0 s e 5 s o movimento c progressivo c retardado.
b) entre os instantes 15 se 20s a aceleração escalar é negativa.
c) entre os instantes 5 se 10s o movimento c progressivo retardado.
d) no instante 15 s a aceleração é nula.
c) nos instantes 10 s c 20 s a aceleração atinge seus valores máximos.

58. S I
21. CESCEA — Dois corpos, distantes entre si 100 m. partem simultaneamente
um em direção ao outro, ao longo ca reta que os une. O gráfico abaixo
marca a posição de cada um dos corpos no decorrer do tempo; (1) rcfcre-se
ao primeiro e (2) ao segundo corpo.
Considere as proposições:
I) Os corpos seencontram noinstante t = 4 s.
II) Os espaçospercorridos pelo corpo (1) e pelo corpo (2) desde o mo­
mento da partida até o instante de encontro são. respectivamente.
—
f>
()m c 40 m.
III) A velocidade média do corpo (1), em módulo, durante os primeiros
6 s. é maior que a do corpo (2).
São corretas as proposições:
a) I e II. d) Todas são verdadeiras.
b) I c III. c) Todas são falsas.
c) II e III.
22. CESGRANRIO — Um mau motorista percorre uma avenida onde os su­
cessivos sinais dc tráfego são eqüidistantes e estão sincronizados para que
um bom motorista possa cruzar todos os sinais no verde, dirigindo com
uma determinada velocidade constante.

59. No entanto, o mau motorista não aproveita essa chamada "onda verde .
Ele arranca subitamente, “queimando borracha", na abertura de um sinal,
acelera a fundo e depois freia violentamente de modo a parar no sinal
seguinte, onde aguarda a abertura, c assim por diante.
Qual dos seguintes gráficos posição x tempo melhor representa o movimento
do carro desse mau motorista? <
Tempo
Posição
Tempo

60. 62
23. UNIVERSIDADE DO RIO GRANDE DO NORTE — Ao fa^er uma
viagem de carro entre duas cidades, um motorista observa que sua velo­
cidade escalar média foi de 70 km/h, e que, em média, seu carro consu­
miu 1,0 litro de gasolina a cada 10 km. Se. durante a viagem, o motorista
gastou 35 litros de gasolina, quantas horas demorou a viagem entre as
duas cidades?
a) 3 h d) 4 h e 30 min
b) 3 h c 30 min e) 5 h
c) 4 h
2. I) Imagino um observador A dotado dc velocidade V em relação a uma
escada rolante B, que sobe também com velocidade V. em reiação à Terra
(C). Se A subir a escada B. a velocidade de A com relaçáo a C será 2V
(movimento).
Se A descer a escada B. a velocidade de A em relação a C será zero
(repouso).
Conclusão: I está errada
II) Estando A oarado em relação a B. então A c B estão permanentemente
unidos, podendo ou não o conjunto estar em movimento.
Sc B está parado em relação a C, então B e C estão permanentemente
unidos.
Então, A. B e C estão formando um único sistema rígido (um triângulo,
por exemplo), onde cada um dos pontos está em repeuse em relação
aos outros.
Conclusão: II está certa.
Rosposta: b.
3. b (Por espaço percorrido entenda-se deslocamento escalar AS.)
4. a (Vm:= 54 km/h)
5. a 6. b 7. c 8. b 9. b 10. a 11. a 12. d
13. e (Movimento progressivo^- movimento descrito a favor da orientação dc
referencial.)
14. c 15. c 16. a 17. d 18. b 19. d
20. c (Importante: não se define aceleração quando há formação de “bico"
no gráfico V x t. Isto. por exemplo, ocorre nos instantes t = 5s e
t = 15 s.)
21. a 22. b 23. c

62. Definição de movimento uniforme
O movimento de um móvel é uniforme quando sua velocidade
escalar é constante e não-nula.
Assim, um automóvel dotado de movimento uniforme terá seu
velocímetro indicando sempre o mesmo valor:
Movimento
uniforme
• Rap dez constante em qualquer trajetória.
• Sentdo do movimento sempre constante
• A indicação do velocímetro é sempre a mesma.

63. Movimento uniforme em trajetória curvilinea.
RAPIDEZ CONSTANTE
Resumindo: MU V constante e não-nula
• Conseqüências da definição — Como conseqüência dessa defi­
nição. podemos concluir que. no movimento uniforme, a aceleração
escalar é constante e nula.
Ou seja: MU => aceleração escalar é nula
Como a velocidade escalar é constante, o valor da velocidade
escalar instantânea, no movimento uniforme, coincide com o da velo­
cidade escalar média.
Isto é: MU •=> V = V™

64. 66
Instante qualquer (t)
Instante inicial (t 0)
Função horária do movimento uniforme
A expressão matemática que relaciona os espaços S de um móvel
(indicativos de suas posições) e os correspondentes instantes t é
denominada função horária do movimento, sendo representada gene­
ricamente por S = f(t).
S indica a posição do nevei num instante
t quaiquer.
§o mdica a posição do móvel para trrO .
e . w w AS S - S „ S - S .
Sendo V — Vm— -----= ----------- , então: V = --------
At t - 0 t
=> S = S »-f Vt (função horária do movimento).
Conclusão: A função horária do movimento uniforme é do 1.° grau
na variável t, sendo expressa por: S — So 4- Vt
i S0 (espaço inicial) indica a posição ocupada pelo móvel n
onde ' instante inicial do movimento (instante zero)-.
! V é a velocidade escalar constante e não-nula.

65. Exem plos:
S = 6 + 2t (SI)
S = - 3 - 8t (SI)
í Sm= +6 m
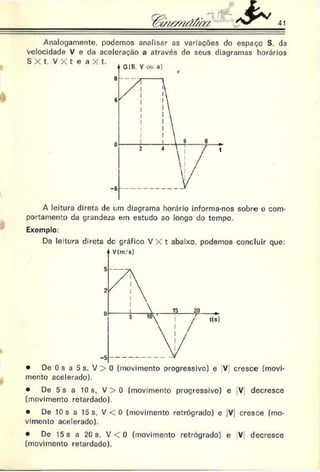
[V = +2 m/s (movimento progressivo]
í Sm= —3 m
[ V — —8 m/s (movimento retrógrado)
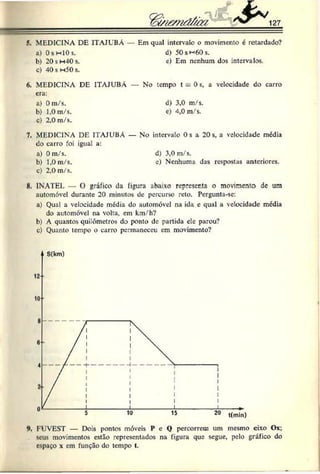
S — 5t (SI)
(wô0VO(tft%L____
S<
i = 0
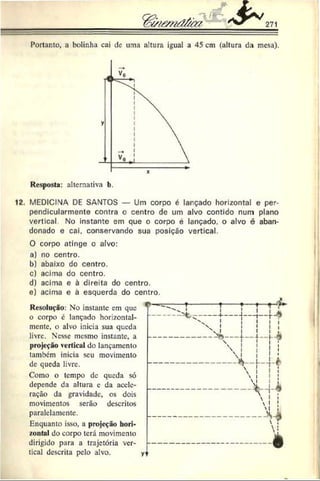
V = 5 m/s (movimento progressivo]
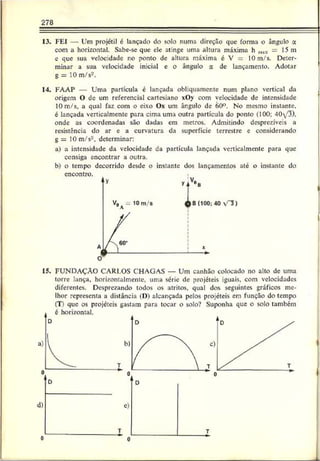
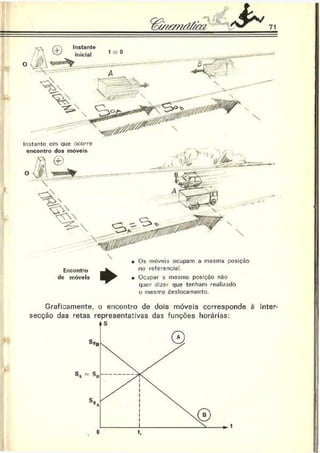
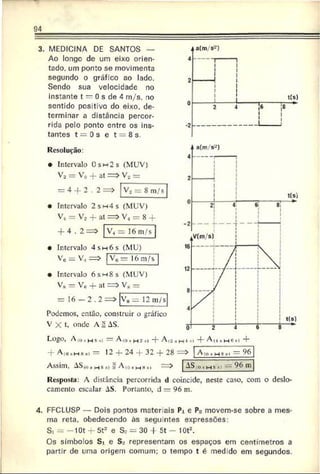
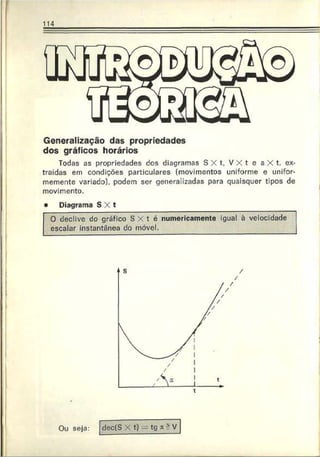
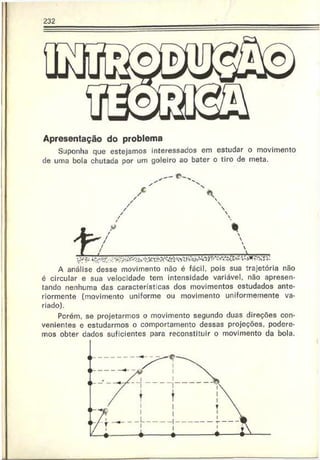
1. A funçãc horária informa sobre o tipo de movimento desenvolvido pelo
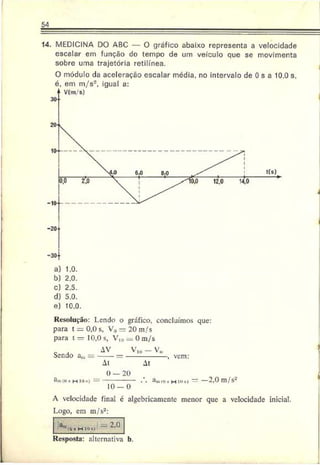
móvel mas nada informa a respeito da trajetória seguida pelo corpo.
2. É importante o conhecimento das posições ocupadas pelo móvel ao longo
do tempo. Onde estará o móvel nos instantes t = 10 s. t = 20 s e t = 30 &?
A função horária respondo a esta pergunta!

66. 68
3. Observo que o espaço S de um móve pode obedecer a uma corta função
horária, porém em trajetórias diferentes. A função horária ntíica como
o móvel caminha e não onde o movei caminha Com apenas a função
horária não podemos prever a trajetória co movei.
S
Diagramas do movimento uniforme
• Diagrama S X t — A representação gráfica da função horária do
movimento uniforme é uma reta inclinada em relação ao eixo hori­
zontal, pois é uma função matemática do 1.° grau em t.
g __g(
Lembrando que S = S.. 4 Vt. então V = -------- — (1).
t
Observando-se o diagrama S X t seguinte, podemos escrever:
S - Sn
dec = tg a
t
( 2).

67. Comparando (1) e (2), concluímos: o declive do gráfico S X t no
movimento uniforme é numericamente igual à velocidade escalar do
móvel.
Ou seja: dec ( S X t ) N
=V
v i
rapidez constante
STZ I j
• Diagrama V X t — O diagrama V X t referente ao movimento
uniforme será representado por uma reto paralela ao eixo dos tempos,
já que a velocidade escalar neste movimento é constante e não-nula.
Neste gráfico, calculando a área sob a reta, podemos escrever:
A 3 V t (1).
Como S = So + Vt, então S — So = Vt => AS = Vt (2).
Comparando (1) e (2). concluímos: a área sob o gráfico V X t
no movimento uniforme é numericamente igual ao deslocamento
escalar do móvel, no intervalo de tempo considerado.
Ou seja:
(M terrxjfâú-___
A (V X t) 2 AS
Como no movimento uniformo a aceleração escalar ó constantemente nula.
o diagrama a X t será representado por uma reta coincidente com o eixo
dos tempos.

68. 70
Exemplo:
Seja a função horária S -
— 2 + 1 .5 t, no SI:
para t — 0 s, S,. — 2 m;
para t — 4 s. Sí _ 8 m.
Podemos, então, construir o
diagrama S X t.
Nesse gráfico, notamos que
dec
8 - 2
(«» H « «> —
4 — 0
= 1,5 => dec = 1,5
Da função horária, temos
V - 1,5 m/s
Logo. o declive do gráfico
S X t é numericamente igual à
velocidade escalar do móvel.
Neste gráfico, notamos que
A(o«h íh »— 4 . 1,5 = 6 —>
L
(0»H
-»«
>= 6
Da função horária, temos
S4— 8 m e So — 2 m.
Logo: ASm«h i »i — —
- So = 8 - 2 = 6 =>
AS :oRh t •) — 6 m
0 1 2 3 4 tis)
Portanto, a área sob o gráfico V X t é numericamente igual ao
deslocamento escalar do móvel.
Como a aceleração escalar é constantemente nula. o gráfico a X t
será uma reta coincidente com o eixo dos tempos.
Encontro de móveis
Quando dois móveis percorrem a mesma trajetória orientada,
poderá ocorrer encontro entre eles. Isto acontecerá quando suas
posições coincidirem, ou seja, quando seus espaços forem iguais,
desde que referidos à mesma origem.

69. Instante
inicial
Instante cm que ocorre
encontro dos móveis
71
Encontro
de móveis
• üs móveis ocupam a mesma posição
no referencial.
• Ocupar a mesma posição não
quer dizer que tenham realizado
o mesmo deslocamento.
Graficamente, o encontro de dois móveis corresponde è inter-
secção das retas representativas das funções horárias:

70. 72
Apêndice
A propriedade referente à área do diagrama V X t pode ser
generalizada para qualquer tipo de movimento. Todavia, a demons­
tração desta propriedade envolve uma matemática mais refinada que
será desenvolvida no volume referente à Dinâmica.
Resumindo, para qualquer tipo de movimento: A {V X t ) ? A S
1. UNIVERSIDADE DO PARANÁ
— Três móveis A. B e C par­
tem, simultaneamente, em
movimento uniforme e reti­
líneo, dos pontos a, b e c.
com velocidades constantes,
respectivarnente iguais a V* = 15 m/s, VB = 4,5 m/s e
Vc = 7.5 m/s. Pede-se o instante em que o móvel A estará entre
os móveis B e C e a gual distância de ambos.
Resolução: Lembrando que no movimento uniforme S = S„ -|- Vt, no
instante inicial, adotando o ponto A como origem dos espaços e orien­
tando a trajetória conforme a figura, temos:
Situaçãc inicial
Situação final

71. L
a
Sd
a = ü m
VA= 15 m/s => SA= 151
B
S,)](= 20 m
= > Sr - 20 -f- 4,5t
C
V» — 4,5 m/s
Soc = 40 m
Sc- = 40 + 7,5t
V0 = 7,5 m/s
Nas condições do enunciado, podemos cscrcvcr: S.v— Sn = Sc — SA
.
Logo, 2S.v — Sii -|- So.
Substituindo as funções horárias dos móveis, teremos:
2(15 t) = (20 -f 4,51) -f (40 + 7,5t) = > 30t = 60 + 12t =>
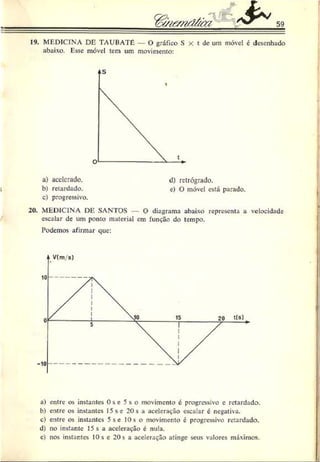
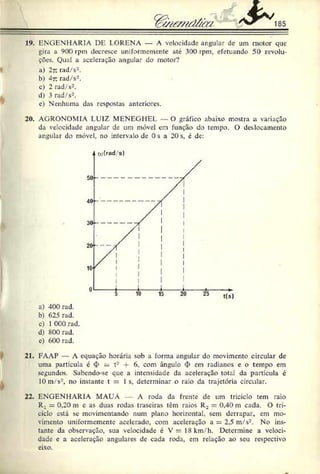
=> I8t = 60 = > L= ------=>
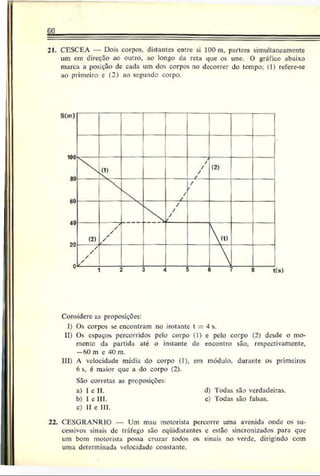
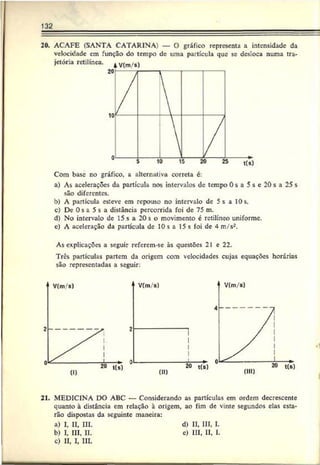
18
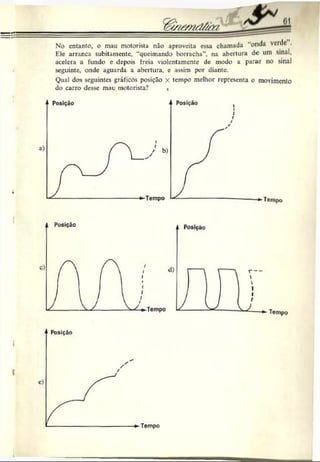
Resposta: O móvel A estará equidistante de B e C ------s após o início
da contagem dos tempos.
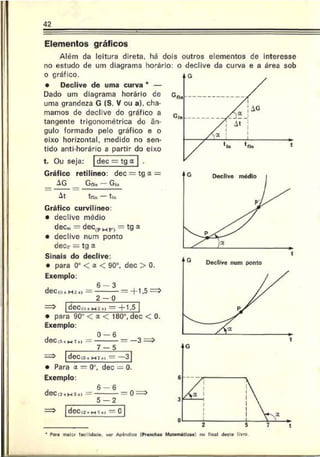
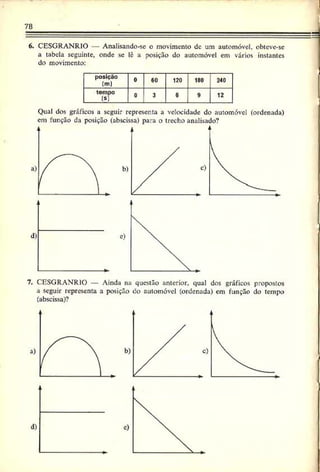
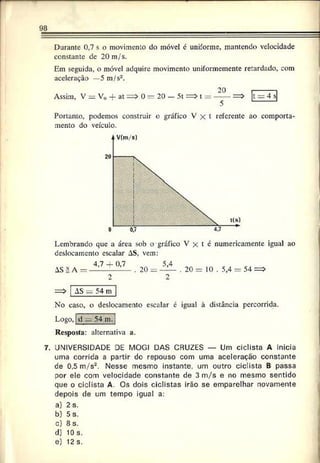
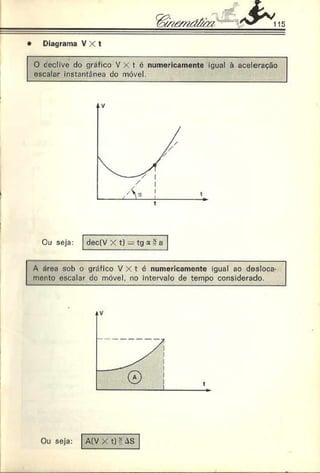
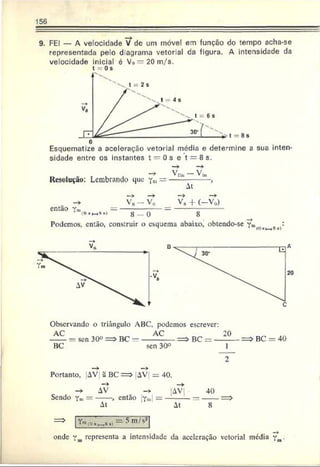
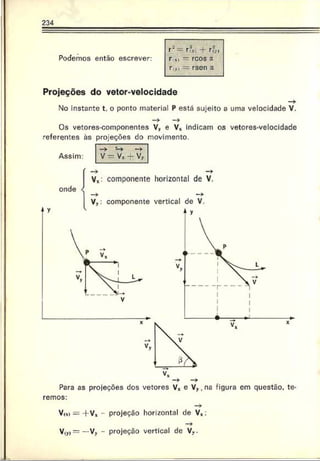
2. AMAN — Para passar uma ponte de 50 m de comprimento, um
trem de 200 m, a 60 km/h, leva:
a) 0,35 s.
b) 1.5 s.
c) 11,0 s.
d) 15,0 s.
e) 30,0 s.
Resolução: Adotando o início da ponte como origem do referencial,
orientando-o no sentido do movimento e observando o esquema abaixo,
podemos escrever, para a dianteira do trem:

72. 74
Instante zero
So = 0 m
V = 60
km
Portanto, S = S„ | Vt
h
S =
60 m
3,6 s
60
3,6
. t.
Completada a travessia, teremos S = L —d = 200 -|- 50 = 250 m.
Assim: 250 =
60
. t t =.-
25 . 3,6
3,6
t = 25 . 0,6
t = 15 s
Resposta: alternativa d.
3. MEDICINA DE VASSOURAS Um móvel A com movimento reti­
líneo uniforme parte do ponto a cm direção a b, com velocidade
de 90 km/h. No mesmo instante, sai de b um móvel B, também
com MRU. A distância retilínea ab é de IG km. A velocidade do
móvel B, para que ambos sc cruzem a 6 km de a. deve ser igual a:
a) 80 km/h.
b) 16.67 m/s.
c) 37.5 m/s.
d) 25 m/s.
e) 22,22 m/s.
Resolução: Adotando como origem dos espaços o ponto a c orientando
a trajetória conforme o esquema a seguir, notamos que:
Móvel A: SoA= 0 k m
V A=: 90 km/h
Móvel B: SoH= 10 km

73. T o w ém O fà a 75
Assim, podemos escrever:
SA= SoA-f VA
t = > SA= 901 (1)
S„ = Son + V„t = > SB= 10 + V„t (2)
Condição de encontro: SA= SB= 6 km.
Logo, substituindo em (1),
6
6 - 901 = > t = ------= >
90
Voltando cm (2), temos:
vem:
I
t = ------h
15
(instante de encontro)
6 = 1 0 - * VB Y'u — 60km/h
O sinal menos (—) indica que o movimento é retrógrado.
Então:
km J 000 m
V„! = 60-----= 60 . ----------- = í 6,67 m/s =>
h 3 600 s
Conclusão: o móvel B deverá ter velocidade escalar de intensidade
16,67 m/s.
Resposta: alternativa b.
|VB| = 16,67 m/s
4. MEDICINA DE ITAJUBA — O
gráfico ao lado descreve o
movimento retilíneo de 2
carros A e B que viajam na
mesma direção. Podemos
afirmar com certeza que:
a) o carro A está perdendo
velocidade enquanto o
carro B ganha velocidade.
b) o carro A parou no ins­
tante t = 100 s.
c) os dois carros estão ro­
dando na mesma d reção
e em sentidos contrários.
d) o carro A está mais ace-
lerado que o carro B.
e) no instante t = 50 s os
dois carros têm a mesma
velocidade.
Resolução: Lembrando que o declive do gráfico S — f(t) é numerica­
mente igual à velocidade escalar do móvel, observamos que tanto o

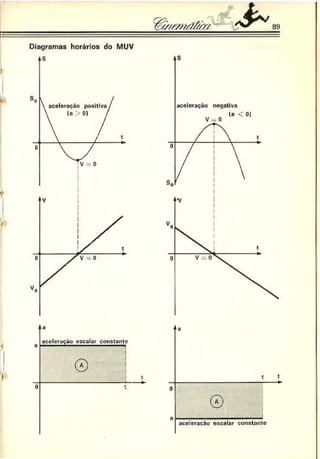
74. 76
carro A como o B possuem velocidades constantes e nâo-nulas (uma
reta tem declive constante). Podemos, então, escrever:
1) carro A: 90« < a < 180° decA < 0 => VA< 0
(movimento retrógrado)
2) carro B: 0° < j3 < 90° decB > 0 VB > 0
(movimento progressivo)
Note que, no instante t = 60 s, os
móveis ocupam a mesma posição,
e que, no instante t = 100 s, o mó­
vel A está na origem do referencial
(S = 0 m).
Resposta: alternativa c.
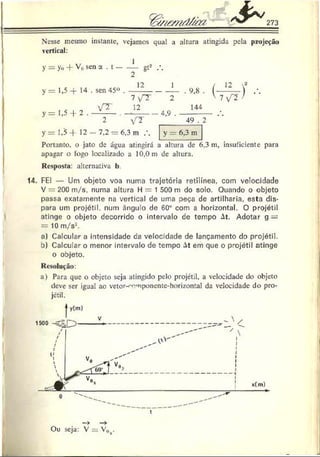
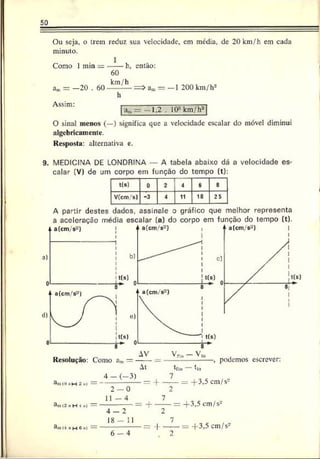
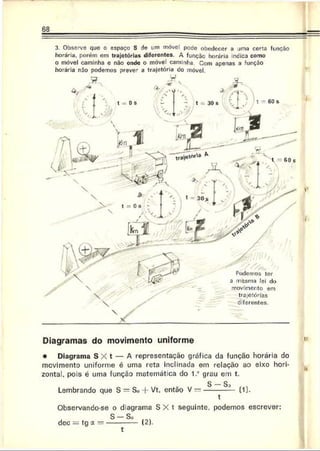
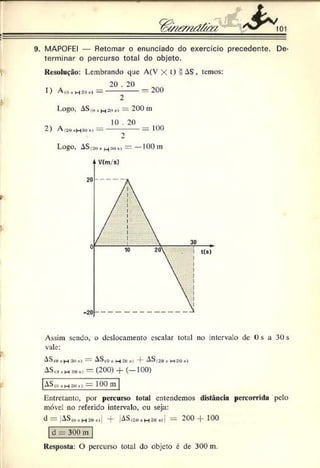
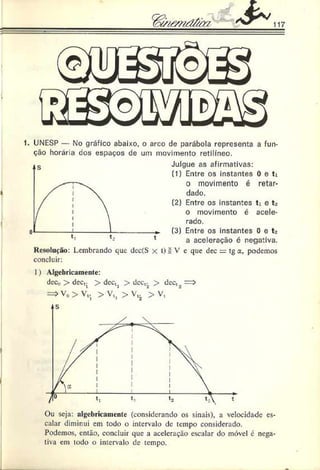
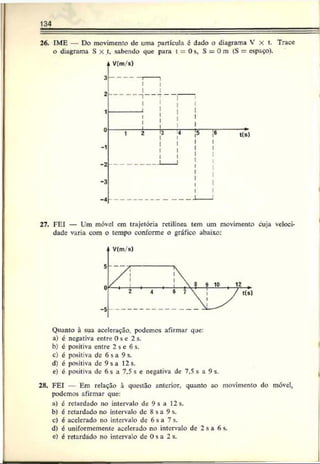
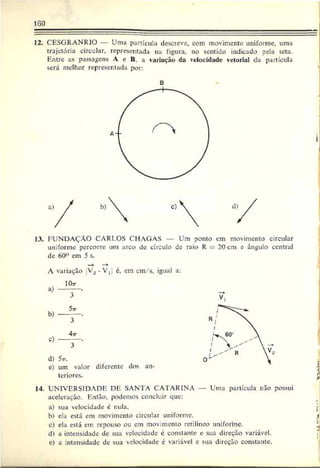
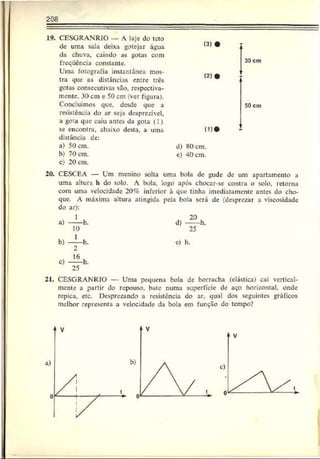
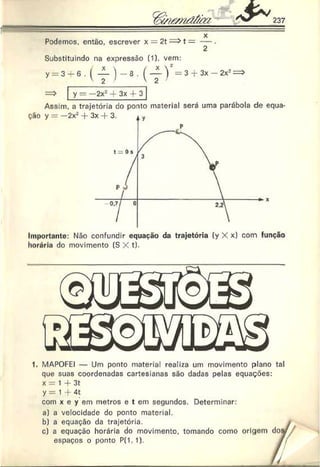
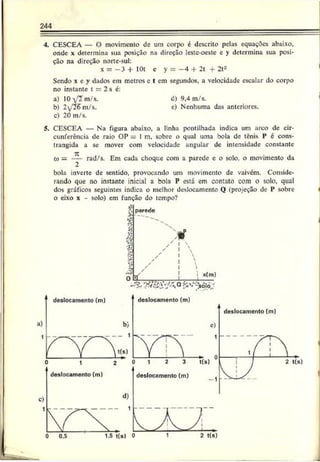
5. IMS — Uma partícula percorre, durante 10 segundos, uma tra­
jetória "etilínea com uma velocidade que varia com o tempo se­
gundo o gráfico abaixo. Pode-se afirmar que a velocidade média
da partícula nesses 10 segundos é. em m/s, igual a:
V(m/s)
10]
8
6
-
i
i
i
i
i
2
1 1 1
0 2 4 6 8 10
a) 6.
b) 5.6. d) 0.8.
c) 1.3. e) 0.4.
Resolução: Como no gráfico V - í(t) a área sob a curva é numerica­
mente igual ao deslocamento escalar do móvel, podemos escrever:
A(0-m i ,> = 4 . 8 = 32 —r ASm»h •
» ~ 32 m _
A(4 hm i<
>
s) = 6 . 4 = 24 >AS(.j.. m io »i = 24 m
—
—
^ AS,0ü ioi) — 3z -f- 24 = 56 m
AS((| 10M
l
) --
( O f lH lO i)
56
Sendo V„ vem:
At(0 » H 10 *í
V..
(0•w 10 M
) 10
V,„ — 5,6 m/s
lO*H 1
0“
Resposta: alternativa b.

75. 1. UNIVERSIDADE DO ESPÍRITO SANTO — Um móvel percorre o
segmento de reta AC com velocidade constante, onde AB ^ BC. Se t, c t»
são os tempos gastos, respectivamente, nos percursos AB e BC, é verda­
deira a seguinte relação:
A E C
a) AB/t, = BC/to d) AC = AB/t, + BC/t2
b) AB/BC = t2/t, e) AC = (AB + BC)t,to
c) AB/BC = (ta/t,)2
2. I-El A luz demora 10 min para vir do .Sol à Terra. Sua velocidade é
3 . 103km/s. Qual a distância entre o Sol e a Terra?
3. FAAP — Qual c a distância da Terra a uma estrela cuja luz é recebida
após 5 anos?
4. FACULDADES DO INSTITUTO ADVENTISTA — O tempo gasto por
um trem de 100 m para atravessar um túnel de 200 m. deslocando-se com
uma velocidade escalar constante dc 72 krn/h, é de:
a) 5 s. d) 15 s.
b) 15 h. e) 20 s.
c) 10 s.
5. CTA (COMPUTAÇÃO) — Um móvel descreve uma trajetória retilínea com
velocidade constante dc 2 m/s. Nessas condições, o gráfico cartesiano de
sua velocidade em função do tempo será:
a) uma reta paralela ao eixo dos tempos.
b) uma reta paralela ao eixo das velocidades.
c) uma reta que passa pela origem.
d) uma reta com coeficiente angular 2 e coeficiente linear 4.
e) Nenhuma das respostas anteriores está correta.

76. 78
6. CESGRANRIO — Analisando-se c movimento de um automóvel, obteve-se
a tabela seguinte, onde se lê a posição do automóvel em vários instantes
do movimento:
posição
(m)
0 60 120 180 240
tempo
(»1
0 3 6 9 12
Qual dos gráficos a seguir representa a velocidade do automóvel (ordenada)
em função da posição (abscissa) para o trecho analisado?
d) e)
7. CESGRANRIO — Ainda na questão anterior, qual dos gráficos propostos
a seguir representa a posição cio automóvel (ordenada) em função do tempo
(abscissa)?
d) c)

77. 8. FEI — O gráfico dos espaços para um móvel é dado pela figura:
O gráfico das velocidades correspondente é o dado por:
9. UNIVERSIDADE DE BRASÍLIA — Um móvel desloca-se ern linha reta
de um ponto X a um ponto Z, passando pelos pontos Y c S. A distância
entre cada ponto é a mesma e o movimento ó assim descrito: de X para Y
6 gasta 1h, à velocidade constante; de Y para S o móvel desloca-se com
metade da velocidade do trecho XY e de S para Z com o quádruplo da
velocidade do trecho YS. 0 tempo total gasto no percurso c dc:
a) 4 h. c) 3 h 30 min.
b) 6 h. d) Nenhuma dessas.

78. 80
10. UNIVERSIDADE DE BRASÍLIA — Na questão anterior, se o trecho XY
tem 70 km, a velocidade média no percurso de X a Z é de:
a) 35 km/h. c) 60km/h.
b) 52,5 km/h. d) 70 km/h.
11. CESCEA — O gráfico representa, cm forma aproximada, o movimento de
um carro durante certo percurso.
A velocidade média do carro
nesse percurso é de:
a) 20 km/h.
b) 30 km/h.
c) 32km/h.
d) 40 km/h.
c) Não há dados suficientes para
o cálculo.
12. CESCEA Um cachorro encontra-se entre seu esconderijo e o laçador,
a 50 m do primeiro e a 100 m do segundo, numa mesma reta. Inicia-se a
perseguição, o cão com velocidade constante de 3 m/s, dirigindo-se ao
- esconderijo, o homem, com velocidade, também constante, de 8 m/s, no
encalço do cão.
a) O laçador alcançará o cão 15 m antes do esconderijo.
b) O laçador alcançará o cão 1s antes do esconderijo.
c) O laçador está a 15 mdo cão quando este alcanÇa o esconderijo.
d) O laçador alcançaria o cão até o esconderijo se sua velocidade fosse, no
mínimo, três vezes a do cão.
e) O laçador alcançaria o cão sc dispusesse de mais 1s antes de o cão entrar
no esconderijo.
13. MEDICINA DO ABC Dois foguetes espaciais são enviados, a partir da
Terra, com 48 h de intervalo. O primeiro a scr enviado tem velocidade
constante dc 30 000 km/h c o segundo, de 40 000 km/h. Ambas as velo­
cidades têm o mesmo sinal. O sistema de referência é a Terra.
Para que o primeiro foguete seja ultrapassado pelo segundo, este último
deverá voar durante o seguinte número de horas:
a) 96. d) 192.
b) 144. c) 288.
c) 168.
14. FUVEST — Numa estrada, andando de caminhão, com velocidade cons­
tante, você leva 4 s para ultrapassar um outro caminhão, cuja velocidade
é também, constante. Sendo de 10 m o comprimento dc cada caminhão, a
diferença entre sua velocidade e a do caminhão que você ultrapassa c, apro­
ximadamente, igual a:
a) 0,2 m/s. d) 5.0 m/s.
b) 0.4 m/s. c) 10m/s.
c) 2,5 m/s.

79. fâ s im id / im
15. PUC (SAO PAULO) — l)o;s automóveis partem, no mesmo instante, das
cidades A e B. percorrendo uma estrada retilínea AB com velocidades de
50km/h e XOkm/h. um em direção ao outro. Ao fim de 2h eles estão a
uma distância dc 40 km um do outro. A distância AB vale:
a) 200 km. d) 160 km.
b) 300 km. e) 240 km.
c) 400 km.
16. FUNDAÇÃO CARLOS CHAGAS — Dois trens (A c B) movem sc em tri­
lhos paralelos, deslocando-se em sentidos opostos. As velocidades escalares
dos trens são constantes e iguais a 30km/h. Cada trem mede 100 in dc
comprimento. Quando os trens se cruzam, durante quanto tempo um obser­
vador no trem B vê passar o trem A?
a) 96 s d) 12s
b) 48 s e) 6,0 s
c) 24 s
17. FAAP — Dois ciclistas distanciados de 60 m um do outro possuem funções
horárias S, = 20 + 2t e S2 ——
40 + 3t, em relação a um mesmo referen­
cial. Verificar quando e onde os dois ciclistas se encontrarão. (Considerar
S| e Sa em metros e t em segundos.)
18. FUNDAÇAO CARLOS CHAGAS — A distância entre dois automóveis
é de 225 km. Se eles andam, um ao encontro do outro, com 60km/h e
90 km/h. ao fim de quantas horas sc encontrarão?
a) Uma hora.
b) Uma hora c quinze minutos.
c) Uma hora c meia.
d) Uma hora c cinquenta minutos,
c) Duas horas c meia.
19. PUC (SÂO PAULO) — Duas partículas cncontram-se inicialmente nas posi­
ções x, = 10cm, y, = 0 cm. x
._
. = Ocm c y2 = 20 cm. com velocidades
V, — 4 . 10‘ cm/s segundo x c Va dirigida ao longo dc y. conforme in­
dica a figura. O valor da velocidade Va para que elas colidam deve ser:
c) -8 . 1
0
**cm/s.

80. 82
20. CESCEA — Dois corpos deslocam-sc ortogonalmente entre si, com veloci­
dades uniformes V, 1.5 m/s e V2 2.0 m/s. No instante t = 0s eles
se encontram na origem de um sistema de referencia xOy. Considerando
que o corpo (I) se desloca ao longo do eixo x c o corpo (2) ao longo do
eixo y. qual a distância que os separa no instante t 2 s?
a) 7.0m d) 1.0 m
b) 5,0 m e) 0,5 m
c) 3.5 m
21. FUNDAÇÃO CARLOS CHAGAS — Um pouco de tinta é colocado na
banda de rodagem do pneu de um carro. Quando o carro se movimenta,
a mancha de tinta deixa marcas no chão. Se estas marcas tiverem a dispo­
sição abaixo, o que se pode concluir sobre a velocidade e a aceleração do
carro?
0 2 4 6 8 10 12 I
a) A velocidade é constante e a aceleração é nula.
b) A velocidade é crescente e a aceleração é constante.
c) A velocidade é decrescente e a aceleração é constante.
d) A velocidade e a aceleração são variáveis.
e) Nada se pode concluir, porque os dados são insuficientes.
9. c 10. c 11. c 12. d 13. b 14. d 15. b 16. e
17- = 140 m: t,#walfo = 60 s.
18. c 19. c 20. b
21. e (Observe que. qualquer oue seja o movimento do carro, as marcas
deixadas no châo soráo sempre as mesmas.)

81. cmïuD
3
M
ovim
ento
Uniform
em
enteVariado

82. 04
Instante inicial (t - 0)
velocidade escalar co móvel
para t = 0.
velocidade escalar do móve!
num instante t qualquer
Definição de movimento uniformemente variado
O movimento de um móvel é uniformemente variado quando sua
aceleração escalar é constante e não-nula.
Instante qualquer (t)
Ou seja: escalar é constante e não-njla

83. III
• Consequência da definição — Como conseqüência dessa defi­
nição, podemos concluir que, no movimento uniformemente variado,
o valor da aceleração escalar instantânea coincide com o da acele­
ração escalar média.
Isto é: MUV a - a„
Funções horárias do movimento
uniformemente variado
*
Y
k
• Função velocidade
y
É importante o conhecimento da rapidez e do sentido do movimento em
cada instante A função velocidade da essas duas informações.
A intensidade da velocidade indica a leitura do velocímetro.
O sinal de velocidade indica o sentido do movimento
Seja um móvel cujo movimento é uniformemente variado de tal
forma que V0 é sua velocidade inicial (instante zero), Vé sua velo­
cidade no instante t e a é sua aceleração escalar constante.

84. V = Vo -h at (função horária da velocidade)
Ç g ; Conclusão: A função veloci­
dade do MUV é dada pela ex­
pressão
v
V — Vo H
” at
A representação gráfica da
função velocidade desse movi­
mento será uma reta inclinada
em relação ao eixo horizontal,
pois é uma função horária do
1.° grau em t.
V — Vo
.Neste gráfico, pocemos escrever dec = tg a = ---------- (1).
V - Vo
Como V — Vo -r at, então a = ---------- (2).
Comparando (1) e (2), concluímos: o declive do gráfico V X t
no movimento uniformemente variado é numericamente igual à ace­
leração escalar do movimento.
Ou seja: dec(V X t)1 a
• Função horária — Lembrando que a área sob o gráfico V X t é
numericamente igual ao deslocamento escalar efetuado por um móvel,
podemos escrever:
A(V X t)s AS, onde AS = S - So.
sendo
í So o espaço inicial do móvel (instante zero).
[ S o espaço do móvel no instante t.
Assim, temos A(V X t ) = S - S<
. (1).

85. 87
• No instante inicia t = 0. o espaço inicial e a velocidade inicial do
móvel são. respectivamente. S0 e Vo
• Num instante qualquer t. o espaço e a velocidade do móvel são.
respectivamente. S e V
• No intervalo de tempo lAt —t - 0). AS é o deslocamento escalar da móvel.
Observando-se o gráfico acima, concluímos:
V + Vo _
A ( V X t ) = ---------- 1 (2).
Comparando (1) c (2). vem:
V • Vo V - f V o
----- - — t = S - S o = > S = So + ----------- t
Sendo V = Vo ■
+
■
at, decorre:
s = s ,1+ ^ ± ü ± ^ t ^ s = s0+ ^ l± ^
S = So + Vot-f----— at2 (função horária do movimento)
2
Conclusão: A função horária do movimento uniformemente
variado é do 2.° grau na variável t. sendo expressa por
S - S., f V.,t |------ at-
2

86. 88
onde
So (espaço inicial) indica a posição ocupada pelo móvel no
instante inicial do movimento (instante zero).
Vo (velocidade inicial) é a velocidade do móvel no instante
I inicial do movimento (instante zero).
{ a é a aceleração escalar constante e não-nula.
Exemplos:
S = 10 — 8t -f- 9t2(SI)
Logo. V = —8 -f 18t
S = —2 + 6t — t2 (SI)
Logo, V — 6 — 2t
S = 5ta (SI)
Logo. V = iOt
So = -HO m
<Vo = - 8 m/s
l a = -f 18 m/s2
So = —2 m
Vo = +6 m/s
a = —2 m/s2
So = 0 m
V., = 0 m/s
a = 4-10 m/s2
Equação de Torricelli
Extraindo o valor de t na função velocidade (V = Vo -f at) e subs­
tituindo-o na função horária ( S —So 4- Vot 4------ at2) cotemos a
expressão Va — V: 4- 2aAS .denominada equação de Torricelli.
Diagramas horários do movimento
uniformemente variado (MUV)
A representação gráfica da função horária do MUV é uma pará­
bola cuja concavidade é voltada para cima (se a > 0) ou para baixo
(se a < 0).
Conforme já fo visto, o diagrama V X t será representado por
uma reta inclinada em relação ao eixo t.
Como a aceleração escalar é constante e não-nula, o diagrama
a X t será representado por uma reta paralela ao eixo dos tempos.
Observando-se a área sob o gráfico a X t, podemos escrever
A = at (1).
Como V = V,. 4- at, então V - Vo = at => AV = at (2).
Comparando (1) e (2). concluímos: a área sob o gráfico a X t
é numericamente igual à variação da velocicade do móvel, no inter­
valo de tempo considerado.
Ou seja: A(a X t ) U V

87. ,1
<
t
t
1
*
i
Diagramas horários do MUV
____________________________________t t
o
aceleracào escalar constante

88. 90
Exemplo:
Seja S — 4 — 5t -f- t2 (SI) a
função horária dc um móvel:
para t = 0 s, Sn = 4 m:
para t = 1 s. Si = 0 m (raiz):
para t = 4 s, Si = 0 m (raiz).
Podemos, então, construir o
gráfico S X t.
Observe que quando t = 2,5 s
a parábola atinge seu vértice,
instante em que o móvel muda
o sentido de seu percurso.
Da função S = 4 — 5t + t2
concluímos que. Vo = —5 m/s e
a = -f 2 m/s2.
Logo. V = —5 -f- 2t.
Para t = 0 s, Vo = —5 m/s;
para t = 4 s. V, = 3 m/s.
Podemos, então, construir o
gráfico V X t.
Nesse gráfico notamos que. para t — 2,5 s, V — 0 m/s, instante
correspondente ao vértice do gráfico S X t.
Examinemos, agora, o. declive do gráfico V X t.
3 - ( - 5 ) _ 8
4 - 0 4
Temos: deCi.. h ^ i = — = > dec<o»M4»i — 2
Assim, observamos que tíecfV X O i a
Como a aceleração escalar é constante, o gráfico a X t será uma
reta paralela ao eixo dos tempos.
Esta reta cortará o eixo das acelerações cm a ~ 2 m/s*.
Observando a área sob o gráfico, concluímos:
A<o«h 4» — 4 . 2 = 8 —^ Ao >
1M
-»*
>= 8
Sabemos que V* = 3 m/s e V.» = —5 m/s.
Logo:
AV<
0sm '• — 8 m/s
AV,;om
h *») — Vi - V o = 3 - (—5) = 8 ==
Assim, a área sob o gráfico a X t é numericamente igual à va­
riação da velocidade escalar do móvel.

89. 91
Velocidade média no MUV
Lembrando que A(V X t ) í AS, no gráfico V X t abaixo temos:
A = . V3 + V~ At => AS = V- + V' A t ^ A ! _ =
2
V ■
+ Vi
At
Conclusão: No MUV. a velocidade média de um móvel é igual
à media aritmética das velocidades escalares instantâneas inicial e
final, no intervalo de tempo considerado.

90. 92
1. ENGENHARIA DE SANTOS — Um ponto material realiza um mo­
vimento sobre uma trajetória retilínea que obedece à função ho­
rária S = t2— 6t + 8. em que S é o espaço dado em metros e
t é o tempo dado em segundos. Podemos afirmar que, a partir
do instante t = 0 s:
a) o movimento é sempre acelerado.
b) o movimento muda de sentido no instante t = 3 s.
c) o ponto material passa pela origem dos espaços apenas no
instante t = 2 s.
d) a aceleração do movimento tem intensidade igual a 4 m/s*.
e) a velocidade do ponto material no instante t — 7 s tem inten­
sidade igual a 9 m/s.
Resolução: Do enunciado, podemos escrever S = 8 — 6 t -f 1 . t2.
Da teoria, sabemos que S S., -f V0t -f----at2.
Assim, concluímos: S.;i = 8 m; V„ = 6 m/s; a = 2 m/s2.
Podemos, então, determinar a função velocidade deste móvel:
V = V„ -f at => fv _ - 6 f 2~t|-
Construindo os gráficos S X t e V X t. chegamos às seguintes con­
clusões:
• O móvel possui movimento ini­
cialmente retrógrado (0 s a 3 s),
parando no instante 3 s para, em
seguida, iniciar movimento pro­
gressivo.
• O móvel passa pela origem nos
instantes t = 2 s c t = 4 s.
• O movimento é inicialmente
retardado (0 s a 3 s) c, em seguida,
acelerado.
Resposta: alternativa b.
I

91. 2. MEDICINA DE CATANDUVA — Um automóvel desloca-se com a
velocidade de 20 m/s. A partir do instante t = 0 s, seu motorista
aplica os freios até o carro parar. Admitindo uma aceleração
constante igual a 4 m/s2, a distância percorrida desde a aplicação
dos freios até a parada do carro é de:
a) 50 m.
b) 5 m.
c) 75 m.
d) 90 m.
e) 25 m.
Resolução: Vamos orientar o referencial associado à trajetória no
sentido do movimento do automóvel.
Neste caso, a distância percorrida ( d ) tem o mesmo valor do desloca­
mento escalar (AS).
Assim: d - A S
Como a velocidade do móvel está diminuindo algebricamente, sua ace
leração será negativa, ou seja. a = 4 m/s2.
Pela equação de Torricelli,' vem:
V/In= V?« + 2aAS = > AS =
2a
AS =
0 =- 2 0 -
2 . ( - 4 )
4(X)
AS — -------
8
= > AS = 50 m : d — 50 m
Resposta: alternativa a.

92. 3. MEDICINA DE SANTOS —
Ao longo de um eixo orien­
tado. um ponto se movimenta
segundo o gráfico ao lado.
Sendo sua velocidade no
instante t — 0 s de 4 m/s, no
sentido positivo do eixo. de­
terminar a distância percor­
rida pelo ponto entre os ins­
tantes t = 0 s c t — 8 s.
Resolução:
• Intervalo 0s h 2 s (MUV)
V2 = V„ + at = »
= 4 + 2 .2 = »
Vo =
Vo = 8 m/s
intervalo 2 s m 4 s (MUV)
V, = Vo + at => V« = 8 4
+ 4 . 2=> |V 4 = 16 m/s
• Intervalo 4 sm 6 s (MU)
Vc = V, = > Vç = 16 m/s
• Intervalo 6 sm 8 s (MUV)
V* = Ve + at =>
= 16 — 2 . 2 = >
Podemos, então, construir o gráfico
V X t, onde A ^ AS.
V„ =
V« = 12 m/s
Logo, Afosi_i $si — A ((», H 3,| + A.o
+ A<t(li-!»*) — 12 + 24 + 32 + 28 :—) A
Assim, AS<„,h 8 » = Aio«mh,, -—
) AS
= 9
6
íOi Mb ' __ 96 m
Resposta: A distância percorrida d coincide, neste caso, com o deslo­
camento escalar AS. Portanto, d = 96 m.
4. FFCLUSP — Dois pontos mater ais Pi e P? movem-se sobre a mes­
ma reta, obedecendo às segu ntes expressões:
S, = —10t + St2 e S_- = 30 + 5t - lOt2.
Os símbolos Si e S„* representam os espaços em centímetros a
partir de uma origem comum; o tempo t é medido em segundos.

93. Pedem-se:
a) o instante em que os dois móveis se encontram.
b) as velocidades e acelerações de ambos nesse instante.
c) a posição do ponto de encontro.
Resolução:
a) Condição de encontro: S, = S>.
Logo: - I0 t -I- 5t2= 30 4- 5t — 1()t2=> 15t2- 15t - 30 = 0 =>
=> t2— t — 2 = 0
(D
- L
O
O
I-
tt) (2 )
Resolvendo esta equação, obteremos t —2 s e t = —1 s. Portanto,
ocorreram dois encontros: o primeiro, 1 s antes de iniciar a con­
tagem dos tempos, e o segundo, 2 s depois de iniciada essa contagem.
Consideraremos como resposta “oficial” o encontro ocorrido no
instante t _ 2 s, pois o estudo dos movimentos é realizado a partir
de t = 0 s.
b) Das funções horárias dadas.podemos concluir:
{
S0l = 0 cm
V, ) 1 = — 1 0 cm/s
ai = 1 0 cm/s2
Logo, V, = V0j -f a,t => V, = —10 + 10t.
| So2 = 30 cm
So = 30 -f- 5t — 10t- I V0;!= 5 cm/s
. a2 = — 2 0 cm/s2
Logo, V2 = Vd 2 -J-a31 => V , — 5 — 20t.
Para t = 2s, vem:
V, = —10+ 10 . 2= > V, — -f 10 cm/s e at = 10 cm/s2
V2 = 5 - 20 . 2 = > V 2 — —35 cm/s c aa = —20 cm/s2

94. 96
c) Sendo Si — —10t -f- 5t2, no instante do encontro (t - 2 s) vem:
St = - 10 . 2 -f 5 . 22=> St = - 20 + 20 => St - 0 cm
St = 2 0 • 2 0 =
Assim, o encontro ocorre na origem do referencial.
Diagramas
horários
Resposta: Os dois móveis se encontram no instante t = 2 s. na origem
do referencial, com velocidades de + 10 cm/s e —35 cm/s c com ace­
lerações iguais a 1 0 cm/s2 e — 2 0 cm/s2.
5. PUC (CAMPINAS) — Dois carros A e B movem-se no mesmo sen­
tido com velocidades V3 e Vb, respectivamente. Quando o carro
A está à distância d atrás de B, o motorista do carro A pisa no
freio, o que causa uma desaceleração constante a. Para não haver
colisão entre os carros é necessário que:
а) V„ - Vb = Í2 ã S .
б) V, - Vb> V 2ad .
c) V* — Vb < V 2ad .
d) V . - Vb= 2ad.
e) Vt — Vb = 0.
Resolução: Adotaremos a origem dos espaços no ponto em que o carro
A se encontra quando o motorista começa a frear, e orientaremos a
trajetória no sentido dos movimentos.
B
J »
©
I

95. O carro B possui movimento uniforme. Logo, sua função horária será
S» = Son -f- Vjjt, onde S«B= d e V# = VV
Assim, Sn — d -f- Vbt.
O carro A é dotado de movimento uniformemente retardado, cuja fun­
ção horária será SA= S„A-f- V0v------— at2, onde S„A= 0 c V0a = V„.
Assim, SA_ V.t - at-.
A distância D entre os móveis será dada por D = S v — SA
.
Logo, D = d -j- Vb
t — V„t -j----L at2= >
2
= > D = d -f (Vb — Va)t H
-----— at2.
2
Para que não haja encontro, 1) não poderá se anular, ou seja, a equa­
ção d -f (Vb — V.)t — at* = 0 não deverá ter solução real.
Assim, o delta (discriminante) da equação deverá ser negativo.
Portanto:
1
(Vb- Va)2 - 4 . ---- ad < 0 = > (Vb— V.)2 - 2ad < 0 = ;
2
= > (Vb - V.)2 < 2ad = > (V. - Vb)2 < 2ad
Resposta: alternativa c.
v , . Vb < v-^ãa
6. PUC (SÀO PAULO) — A velocidade de um carro é. no instante
em que o motorista nota que o sinal fechou. 72 km/h. O tempo
de reação do motorista é de 0.75 s (tempo de reação: tempo de­
corrido entre o instante em que o motorista vê o sinal fechar até
aquele em que aplica os freios) e os freios aplicam ao carro um
retardamento uniforme de 5 m/s*. A distância percorrida pelo
carro desde o instante em que o motorista nota que o sinal fechou
até que o carro pare é de:
a) 54 m.
b) 20 m.
c) 14 m.
d) 10 m.
e) 44 m.
Resolução: Do enunciado, temos:
72
V0 = 72 km/h => V0= ----- m/s => V,> = 20 m/s
‘ 6

96. 98
Durante 0,7 s o movimento do móvel é uniforme, mantendo velocidade
constante dc 20 m/s.
Em seguida, o móvel adquire movimento uniformemente retardado, com
aceleração —5 m/s2.
20
Assim, V = V0 + at = > 0 = 20 — 5t = > t = ------=>
5
Portanto, podemos construir o gráfico V x t referente ao comporta­
mento do veículo.
Lembrando que a área sob o gráfico V x t é numericamente igual ao
deslocamento escalar AS, vem:
4,7 _j_o,7 5 , 4
AS ä A = — — :— -— . 20 = — . 20 = 10 . 5,4 - 54 =>
2 2
= > | AS — 54~m~
No caso, o deslocamento escalar é igual à distância percorrida.
Logo, ;d —54 m.j
Resposta: alternativa a.
7. UNIVERSIDADE DE MOGI DAS CRUZES — Um ciclista A inicia
uma corrida a partir do repouso com uma aceleração constante
de 0,5 m /s2. Nesse mesmo instante, um outro ciclista B passa
por ele com velocidade constante de 3 m/s e no mesmo sentido
que o ciclista A. Os dois ciclistas irão se emparelhar novamente
depois de um tempo igual a:
a) 2 s.
b) 5 s.
c) 8 s.
d) 10 s.
e) 12 s.

97. ir
h
& 99
I
Resolução: Adotando como origem dos espaços o ponto onde A 6
ultrapassado por B. como início da contagem dos tempos o instante
em que isto ocorre c orientando as trajetórias no sentido dos movi­
mentos, teremos:
Sa = S„ -f- V0 t -f- — aA
t2, onde
A A 2
S,. =: 0 m
V
,> 0 m/s
A
aA= 0,5 m/s2 = ---- m/s2
2
Logo, SA= — . — t2 = > SA= — t2 (1)
2 2 4
S,>ti - Dm
ü
Móvel B: movimento uniforme.
Sii = S„i{-f- Vj,t f onde
vV» = 3 m/s
Logo, S„ = 3t (2)
Os dois ciclistas irão se emparelhar novamente quando SA= S».
De (I) e (2), vem:
I) t = 0 s (instante inicial)
1 / 1 1
t2 = 3t = > t I ---- t - 3 ) = 0 = > ID — t - 3 = 0 = >
4 V 4 / 4 .
= > |t = 12 s
Resposta: alternativa e.

98. 100
8. MAPOFEI — O diagrama abaixo representa, em função do tempo,
a velocidade de um objeto.
Trace o diagrama da aceleração em função do tempo.
Resolução: Neste caso, temos uma combinação de movimentos unifor­
memente variados. Como o gráfico apresentado c composto por seg­
mentos de reta oblíquos, as correspondentes funções horárias da velo­
cidade representadas são do l.° grau (movimentos uniformemente va­
riados).
Portanto:
1) Intervalo OswlOs:
Levantando-se o gráfico da aceleração em função do tempo, teremos
a seguinte representação:
V(m/s)
4 - 1 0
20 aím/s2)
0 10
-20

99. ¥
' ----------------------
9. MAPOFEI — Retomar o enunciado do exercício precedente. De­
terminar o percurso total do objeto.
Resolução: Lembrando que A(V X O = ^ S , temos:
2 0 .2 0
1) A(o*h aok ) —------------ —200
fr 2
Logo, ASfuR
H 2ô*) = 200 m
2) A !2ú )
—
|:ím«I—
10 . 20
= 100
Logo, AS(aoh(_^som— —100 m
V
Assim sendo, o deslocamento escalar total no intervalo de Os a 30 s
vale:
AS,0,1H 3üs) =: AS(0 , _j 2o “f- AS 120»m :10«I
A S ,0 »H .10»> = (2 0 0 ) -j- ( — 100)
ASii) ,h 3u») — 100 tu
Entretanto, por percurso total entendemos distância percorrida pelo
móvel no referido intervalo, ou seja:
d = |AS,o, H2on) “j- AS(2o•h só*ií — 200 -f- 100
d = 300 m
Resposta: C) percurso total do objeto é de 300 m.

100. 1. CESCEA — Observando-se o movimento retilíneo de um corpo, fazem-se
medidas de seu deslocamento, velocidade e aceleração para sucessivos va­
lores do tempo, o que é mostrado na tabela abaixo:
Tempo(s) Dcslocamento(m) Velocidadcfm/s) Acclcraçãolnvs'-’)
0 1 2 2
1 4 4 2
2 9 6 2
3 16 8 2
4 25 1 0 2
A partir dessa tabela, podemos concluir que a equação horária que descrevo
o movimento entre os instantes t = 0 s e t = 4 s tem a forma algébrica:
a) y = t2 - 3t + 1. d) y = -2 t2 + 2.
b) y = t2 + 2 t - 2 . e) y = t2 + 2 t + 1 .
c) y = 2 l2 -+
- 2 t -f 2 .
2. UNIVERSIDADE DO RIO GRANDE DO SUL — Numa experiência para
analisar o movimento de um móvel, i.m aluno identificou as três posições
(O. P e S) indicadas na figura, obtidas em intervalos de tempo iguais.
-f-
O
H
--- *
---- h
X Y 2
X
As distâncias entre os pontos identificados por letras consecutivas são iguais
e o móvel partiu do repouso em O. Considerando que as três posições
caracterizam o movimento, qual será a posição do móvel no f:m de um
mesmo intervalo dc tempo seguinte, contado a partir do instante cm que
o móvel estava em S?
a) U
b) V
c) X
d) Y
c) Z

101. 103
3. FUNDAÇÃO CARLOS CHAGAS — Na figura seguinte estão assinaladas
as posições (1,2, 3, 4, 5 e 6 ) de um corpo que está em movimento unifor-
mcmentc acelerado sobre uma mesa horizontal. O intervalo de tempo entre
duas posições sucessivas quaisquer é de 1,0s. Na posição I, a velocidade
escalar do corpo é nula.
i r
1'z 3
4 5 ■
I
1,0 m
Qual é o valor da aceleração escalar do corpo?
a) 5.0 m/s2 d) 2,0 m/s2
b) 4,0 m/s2 e) 1,0 m/s2
c) 3,0 m/s2
4. MEDICINA DA SANTA CASA — Uma partícula descreve o movimento
cujo gráfico horário, parabólico, e dado a seguir, mostrando que para
t = 1 s, x 6 máximo.
Os valores da abscissa x são medidos a partir dc um ponto O, ponto dc
origem da reta orientada sobre a qual a partícula se movimenta.
A função horária é:
a) x = 15 + 2t + t2. d) x = 15 + 2t - t2.
b) x = 15 - 2t - t2. 1
c) x = 15 - t + t2. e) x = 15 —2t + — t2.
5. MEDICINA DA SANTA CASA — Em relação à questão anterior, a velo­
cidade da partícula obedece à equação:
a) V = 2 - t.
b) V = - 2 + t.
c) V = 2 - 2t.
d) V = 2 + 2t.
c) V = 1 - 2t.

102. 104
6. MEDICINA DA SANTA CASA — Ainda cm relação à questão n.°
para t = 5 s a aceleração da partícula, em m/s2, é de:
a) zero. d) -f-2.
b) -2 . e) +1.
c) -1 .
7. CESCEA Um ciclista pedala com velocidade constante de 9 km/h du­
rante 2 min; acelera, então, uniformemente, durante 50 s, até alcançar
18 km/h, desacelerando, a seguir, também uniformemente, até parar, em
50 s. O espaço percorrido nesse tempo foi de:
a) 818,5 m. d)612,5 m.
b) 780,5 m. e)575,5 m.
c) 487,5 m.
8. UNIVERSIDADE DE VIÇOSA — Um corpo desloca-se, segundo uma
trajetória retilínea, com velocidade inicial de 20,0 m/s e é acelerado a
8.0 m/s2 durante 5,0 s. O seu deslocamento durante o quinto segundo é,
em intensidade:
a) 56 m. d) 1,56 . 102m.
b) 1,44 . IO2m. c) nulo.
c) 2.00 . 102m.
9. FUNDAÇÃO CARLOS CHAGAS No instante t = 0s. um carro viaja
a 20,0 km/h. Dois segundos mais tarde (t = 2 s), a intensidade de sua
velocidade é de 23,0 km/h e, depois de outros dois segundos (t = 4 s), é
de 26,0 km/h. Com estes dados, pode-se construir a seguinte tabela:
Tempo(s) 0 2 4
Velocidade(km/hJ 20,0 23,0 26.0
Admitindo que a aceleração seja constante, inclusive antes de t —0 s, qual
foi o módulo da velocidade do carro, cm km/h, no instante t — —
3 s, isto
é, ires segundos antes de atingir a velocidade de 20.0 km/h?
a) 14,0 d) 15,5
b) 14,5 e) 17,0
c) 15.0
10. UNIVERSIDADE DE MOGI DAS CRUZES O gráfico abaixo repre­
senta um movimento retilíneo de aceleração constante:
0 1.0 2,0

103. Se x c medido em metros e t cm segundos, então a aceleração do movimento
é de:
a) 1m/s2. d) 4 m/s2.
b) 2 m/s2. e) 5 m/s2.
c) 3 m/s2.
11. MEDICINA DA SANTA CASA Uma partícula subatômica, deslocan-
do-sc com velocidade constante igual a 6 . 10#m/s, penetra num campo
elétrico onde sofre uma desaceleração constante de 1,2 . IO1
3
14m/s2.
A distância em linha reta que a partícula caminha antes de parar, em cen­
tímetros. é de:
a) 5 . 10-«. d) 15.
b) 30 . 10--'. c) 15 . 10-2.
c) 2.
12. MEDICINA DA SANTA CASA
— O movimento de um móvel,
em trajetória retilínea, c repre­
sentado segundo o gráfico ao
lado. sendo S dado em metros c
t em segundos. Podemos afirmar
que a velocidade media c a ace­
leração escalar entre os instantes
2 s e 4 s valem, respectivamente:
a) Vul = 5 m/s ea = 0 m/s2.
b) Vm= 30 m/s e a = 0 m/s2.
c) Vm= 5 m/s e a = 5 m/s2.
d) Vm= 30 m/s e a = 10 m/s2.
c) Vm= 2,5 m/s e a = 10 m/s2.
13. UNIVERSIDADE DO PARÁ — Uma partícula efetua um movimento re­
tilíneo de acordo com o gráfico abaixo. A distância percorrida a partir do
repouso até o instante t = 12 s é :gual a:
a) 93 m.
b) 96 m.
c) 98 m.
d) 241 m.
e) 100 m.

104. 106
14. MEDICINA DE BRAGANÇA — Para o gráfico indicado, a sequên­
cia dos movimentos será:
a) movimento uniforme progressivo, movimento nulo e movimento acele­
rado retrógrado.
b) movimento nulo. movimento uniforme progressivo e movimento acelera­
do progressivo.
c) movimento uniforme progressivo, movimento nulo e movimento retardado
progressivo.
d) movimento nulo, movimento uniforme progressivo e movimento retardado
retrógrado.
e) Nenhuma das anteriores é correta.
15. CESGRANRIO — Arguido sobre as relações entre posição (S), velocidade
(V) e tempo (t) no movimento uniformemente acelerado (com velocidade
inicial nula), um aluno escreveu no quadre-negro o que se lê abaixo:
Porem, eu sei que
Já que S = ---- at2 (1),
2 s
2S
V = ---- (b)
t
t2
de modo que, de
Mas a = (3).
t
(5) e (6),
Logo, dc (2) e (3), S 28 (7)
t t
V 2S
---- = — <4)
t t2 ou, ainda:
ou, ainda: 1
1 =21
V = — (5). (?)
t

105. A conclusão final c obviamente falsa, embora o início do raciocínio
equação (1) — esteja correto.
Qual a relação em que o aluno desviou-se do raciocínio certo?
a) Na relação (2). d) Na relação (5).
b) Na relação (3). e) Na relação (6).
c) Na relação (4).
16. MEDICINA DE SANTOS — Um móvel parte do repouso em movimento
uniformemente acelerado. Percorre 100 m e 120m em segundos sucessivos.
Calcular sua aceleração.
a) 20 m/s2 d) 10 m/s2
b) 40 m/s2 e) Nenhuma das respostas anteriores.
c) 80 m/s2
17. MEDICINA DE ITAJUBÁ — Num movimento retilíneo de aceleração
constante, podemos dizer que a velocidade média é igual à:
a) velocidade final menos a velocidade iniciai.
b) velocidade final menos a velocidade inicial, dividido por dois.
c) velocidade final mais a velocidade inicial, dividido por dois.
d) velocidade final vezes a velocidade inicial.
e) velocidade final vezes a velocidade inicial, dividido por dois.
18. MEDICINA DA SANTA CASA — Um trem tem velocidade de 72 km/h.
Ao frear, é aplicada a desaceleração de 0,4 m/s2. O intervalo de tempo que
o trem demora até parar é, cm segundos, igual a:
a) 5. d) 10.
b) 50. e) 100.
c) 500.
19. MEDICINA DA SANTA CASA — O mesmo trem da questão anterior,
entre o início da freada c a parada final, percorreu a d:stância, cm metros,
igual a:
a) 200. d) 500.
b) 750. e) I 000.
c) 1500.
20. MAPOFEI — Uma composição de metrô parte de uma estação e percorre
I00m com aceleração constante, atingindo 20 m/s. Determinar a acele­
ração a c a duração t dc processo.
21. MACKENZIE — No diagrama
a = f(t), onde a representa a
aceleração dc um móvel c t o
tempo relativo a essa aceleração,
a área A da figura c numerica­
mente igual:
a) à velocidade média do móvel, relativa ao intervalo de tempo ( t , , t a ) .
b) ao deslocamento do móvel, relativo ao intervalo de tempo ( t l t t a ).
c) à variação da velocidade do móvel, relativa ao intervalo de tempo ( t , . t a ).
d) à velocidade inicial do móvel.
c) Nenhuma das respostas anteriores.

106. 108
22. ENGENHARIA MAUA — Um
ponto material descreve uma tra­
jetória retilínea, referida a um
e:xo de abscissas Ox, de tal mo­
do que sua velocidade, ern fun­
ção do tempo, c dada pelo dia­
grama cartesiano ao lado.
a) Desenhe o diagrama da aceleração do ponto, em função do tempo.
b) Determine a distância entre os pontos inicial (para t = 0 s) e final (para
t = 70 s).
23. MAPOFEI — Um móvel realiza um movimento retilíneo com velocidade
dada pela equação V = 1,0 —0,lt (SI). Tomando como origem de coorde­
nadas o ponto em que o móvel se encontra no instante t = 0s, calcule a
aceleração do movimento e o instante t em que o móvel estará mais afastado
da origem.
24. MEDICINA DO ABC O gráfico abaixo representa a velocidade escalar,
em função do tempo, dc um veículo que se movimenta sobre uma trajetória
retilínea. A aceleração escalar instantânea no instante t —10,0s é, cm
m/s2. igual a:
c) 5,0.
25. MAPOFEI Um vagão ferroviário, deslocando-se com velocidade V —
—30 m/s, é desacelerado até o repouso com aceleração constante. O vagão
percorre 100 m antes de parar. Qual a aceleração do vagão?
26. FAAP — Um motorista de automóvel, viajando a 80 km/h, vê um obstáculo
a 500 m. Verificar qual a aeeleração que deve introduzir nos freios para que
possa parar a tempo.
27. FUVEST Um ciclista A inicia uma corrida a partir do repouso, acele­
rando 0,50 m/s2. Nesse instante, passa por ele um outro ciclista B, com
velocidade constante de 5,0 m/s e no mesmo sentido que o ciclista A. Per-
gunta-se:
a) Depois de quanto tempo, após a largada, o ciclista A alcança o ciclista B?
b) Qual a velocidade do ciclista A ao alcançar o ciclista B?

107. 28. ENGENHARIA TAUBÀTÊ — De uma cidade A parte para uma cida­
de B um automóvel com aceleração constante dc 5,0km/h2. Simultanea­
mente, de B parte para A um outro automóvel com velocidade constante dc
50km/h. A distância entre as duas cidades é dc 180 km. Depois de quanto
tempo os dois carros se encontram?
29. ENGENHARIA MAUÁ — A maior aceleração (ou retardamento) tolerá­
vel pelos passageiros de um trem urbano é de 1.5 m/s2. Sabe-se que a dis­
tância entre as estações c de 600 m e que o trem estaciona durante 20 s
cm cada estação.
a) Determine a maior velocidade que pode ser atingida pelo trem.
b) Calcule a máxima velocidade média do trem, numa viagem.
30. ENGENHARIA MAUÁ — Um ponto material descreve uma trajetória
retilínea segundo a equação horária S = 4.0 —5,0t -f 2,5t2 (SI).
a) Trace uma linha reta. marcando sobre c!a os seguintes pontos, com suas
distâncias relativas:
• origem O das abscissas;
• ponto T, onde está o móvel no instante inicial;
• ponto N, onde o móvel tem velocidade nula.
b) Esboce os diagramas cartesianos do espaço, velocidade c aceleração em
função do tempo.
31. ENGENHARIA TAUBATÊ — Um carro scíre uma aceleração constante
de 2 m/s2. Num percurso de A a B, de 4 m. ele sofre uma variação dc
velocidade de 1,5 m/s. Em que instante dc tempo o carro passa no ponto B?
32. ITA — Um móvel A parte da origem O. com velocidade inicial nula. no
instante t0= 0 s, e percorre o eixo Ox com aceleração constante a. Após
um intervalo de tempo At. contado a partir da saída de A. um segundo mó­
vel B parte dc O com uma aceleração igual a na. sendo n > 1. B alcançará
A no instante:

108. 110
33. PUC (CAMPINAS) Um motorista espera o sinal de trânsito abrir.
Quando a luz verde acende, o carro é acelerado uniformemente durante
6 s, na razão de 2 m/s2, após o que ele passa a ter velocidade constante.
No instante em que o carro começa a se mover, ele foi ultrapassado por
um caminhão que vinha no mesmo sentido, com velocidade uniforme de
lOtn/s. Após quanto tempo e a que distância da posição de partida
do carro os dois veículos se encontrarão novamente?
a) 18s c 180 m. d) 19s e 128 m.
b) 15 s e 150 m. c) Nenhum dos resultados anteriores.
c) 12s e 120 m.
34. MEDICINA DE POUSO ALEGRE — Dois carros A e B, deslocando-se
ambos no mesmo sentido, em uma estrada, passam num certo instante por
um mesmo ponto: o carro A, partindo do repouso desse ponto e desenvol­
vendo uma aceleração constante de 4 m/s2, c o carro B com velocidade
constante de 20m/s. Um passará novamente pelo outro após:
a) 80 s. d) 5 s.
b) 10s. e) Um não passará mais pelo outro.
c) 20 s.
35. PUC (SÁO PAULO) — Um carro de corrida A tem velocidade constante
VA= 54 m/s. Ao passar' pelo box de um concorrente B. este parte com
aceleração aB= 4 m/s2, que permanece constante até atingir a velocidade
VB= 60 m/s, que é mantida.
O tempo empregado por B para alcançar A é de:
a) 75 s. d) 15s.
b) 60 s. c) 10 s.
c) 20 s.
36. FEI — Um móvel parte de um certo ponto com um movimento que obe­
dece à seguinte lei horária: S = 4t2, válida no SI. S é a abscissa do móvel
c t o tempo. Um segundo depois, parte um outro móvel do mesmo ponto
do primeiro, com movimento uniforme c seguindo a mesma trajetória. Qual
a menor velocidade que deverá ter esse segundo móvel, a fim de encontrar
o primeiro?
37. FAAP — Dado o gráfico da variação das velocidades de dois móveis em
função do tempo, e sabendo que até o instante tx o móvel A já havia per­
corrido 10 m, calcular:

109. 111
a) o espaço percorrido pelo móvel B até o instante t,.
b) o instante t2, até o qual os dois móveis terão percorrido espaços iguais.
38. ENGENHARIA MAUÁ — Um móvel parte do repouso de um ponto A
executando um movimento retilíneo, uniformemente acelerado, sobre uma
reta AB. No mesmo instante, parte do ponto B. rumo a A, um outro móvel
que percorre a reta AB com velocidade constante. A distância entre os
pontos A c B c d 50 m. Depois de 10 s da partida, os móveis se cruzam
exatamente no meio da distância entre A e B. Determine:
a) a velocidade do móvel que partiu de B.
b) a velocidade com que o móvel que partiu dc A irá chegar em B.
1. o 2. d 3. d 4. d 5. c 6. b 7. d 8. a 9. d 10. b 11. d 12. d
13. a 14. a 15. e 16. a 17. c 18. b 19. d
20. a = 2m/s2; t = 10s.
21. c
22. o) *aCm/s~)
0 5 10 15 20 2Í5 30 35 40 4^ 50 55 60 65 70 t(s)
-0.4
b ) d = 0 m
23. a ——O.f m/s2; t = 10 s.
24. b
25. a = —4,5 m/s2
26. a a —0.5 m/s2
27. a) t = 20s;
b ) Vv = 10m/s.
28. t * 3,1 h (Após a partida dos móveis.)
29. a) 30 m/s;
b) 10m/s.

110. 112
30. a) 0 1 2 3 4
1
---1---1---1---*
—i---*
--- *
---*-
O N T
S(m)
31. 0,75 s após ter passado por A.
32. e 33. a 34. b 35. a
36. Vm
Jn = 16 m/s
37. a) ASU = 15 m;
b) to = 2 s.
38. a) Vj, = 2.5 m/s:
b ) v a — V50 m/s = 7,1m/s.

112. Generalização das propriedades
dos gráficos horários
Todas as propriedades dos diagramas S X t, V X t e a X t. ex­
traídas em condições particulares (movimentos uniforme e unifor­
memente variado), podem ser generalizadas para quaisquer tipos de
movimento.
• Diagrama S X t
O declive do gráfico S X t é numericamente igual à velocidade
escalar instantânea do móvel.
Ou seja: dec(S X t) - tg a NV

113. • Diagrama V X t
fâ / tfm á â à i
O ceclive do gráfico V X t c numericamente igual à aceleração
escalar instantânea do móvel.
Ou seja: dec(V X t) —tg a ? o
A área sob o gráfico V X t c numericamente igual ao desloca­
mento escalar do móvel, no intervalo de tempo considerado.
Ou seja: A(V X t) ? áS

114. 116
• Diagrama a X t
A área sob o gráfico a X t é numericamente igual à variação da
velocidade escalar do móvel, no intervalo de tempo considerado.
Ou seja: A(a X t) I AV
Resumindo:
Gráficos
Operação
S X t V X t a x t
Leitura
direta
espaço:S
deslocamento
escalar: AS
velocidade
média: V,,,
velocidade: V
variação da
velocidade: AV
aceleração
média: am
aceleração: a
Declive
velocidade
instantânea: V
aceleração
instantânea: a
Não tem
significado
físico.
Área
Não tem
significado
físico.
deslocamento
escalar: AS
velocidade
média: Vin
variação da
velocidade: AV
aceleração
média: am

115. 1. UNESP — No gráfico abaixo, o arco de parábola representa a fun­
ção horária dos espaços de um movimento retilíneo.
i
Resolução: Lembrando que dec(S
concluir:
Julgue as afirmativas:
(1) Entre os instantes 0 e ti
o movimento é retar­
dado.
(2) Entre os instantes ti e t*
o movimento é acele­
rado.
(3) Entre os instantes 0 e t>
a aceleração c negativa.
t) £ V e que dec = tg a, podemos
1) Algebricamente:
dec,? > dec,j > dectj > dec,;, > dec,.,
= » V „ > V t, > V C
j > V,. > V,
Ou seja: algcbricainente (considerando os sinais), a velocidade es­
calar diminui em todo o intervalo de tempo considerado.
Podemos, então, concluir que a aceleração escalar do móvel é nega­
tiva em todo o intervalo de tempo.

116. 118
2) Km módulo:
• jdecol > dec^ | > jdcct( | = > V (,| > V .^ > |V t i[
Ou seja: de 0 a ti o movimento será retardado (intensidade da velo­
cidade diminui).
• |dectJ < jdcct.2 ! < |dcctJ => |Vtj < |Vt/ < V J
Ou seja: de tt a t2 o movimento será acelerado (intensidade da velo­
cidade aumenta).
Resposta: Todas as afirmativas são corretas.
2. FEI — Um móvel desloca-se de forma qje sua velocidade escalar
em função do tempo segue a lei representada no gráfico:
a) Determinar a velocidade escalar média do móvel entre os ins­
tantes t = 1 s e t = 4 s.
b) Representar graficamente a aceleração do móvel em função
do tempo.
Resolução:
a) Lembrando que A(V x t) - AS, vem:
A (i ,i m;i „,
A(í *h i *)
2 ~r 1
2
1 . 10
2
. 10= 15 = > AS.i ,H3,i = 15 m
I
= 5 => AS(SsH-*o
» 5 m / área abaixo
do eixo t /
Sendo AS(i „w*»
>— ASti sM:i -T AS<3»h-
i
temos AS,i *H., s) — 10 m.
AS 10 10
Como Vm—------, então Vm = --------- = —
At 4 — 1 3
10 m
v n, ------ — 3,33 m/s
•1«H4(| 3 s
Portanto:

117. b) Coir.o dcc(V x t) =a, temos:
10 — 0
• deC(o«Hi oi = -------------= 10 = > a,U
BH , *
>= 10 m /s2
1 — 0
1 0 -1 0
• dec(1K
M- 8j — — 0 —i' â<t *h 2 «I — Oin/s*
2 - 1
0 — 10
• dec<2*H3*
>= -------------= —10 = > al2,4M:;*> = —10 m /s2
3 - 2
• dec(3 «Hiii —------------ — —10 — s at3 M
H.| — —10 m js-’
4 - 3
• dec
0 — ( — 10)
H>HÓ»i — 10 a,, sh i »í = 10 m/s2
3. MEDICINA DE TAUBATÉ — Dois móveis A e B passam por um
ponto P em um instante t = 0 s e percorrem a mesma reta. Co­
nhecendo os diagramas das velocidades para os dois móveis, po-
demos afirmar que:
a) os móveis tornam a se
encontrar após 12 s.
b) os móveis tornam a se
encontrar após 24 s.
c) os móveis não mais se
encontram.
d) os móveis tornam a se
encontrar após 30 s.
o

118. 120
Resolução: Lembrando que.no diagrama V X t,dec = a, vem:
móvel A: aA= -J-
40
móvel B: aB=
30
60
30
aA= 4 - — m/s2, constante;
3
aa = —2 m/s2, constante.
Adotando a origem do referencial no ponto F por onde os móveis pas­
sam no instante t —0 s e levando em conta que os movimentos são
uniformemente variados (acelerações escalares constantes), podemos
escrever:
S0 — 0 m
móvel A V0 = + 2 0 m/s
A
móvel B
aA= 4“ — m/s2
S t = 0 m
V0b = 4 - 6 0 m/s
=
>
SA= 20t 4 -------i2 (1)
3
Sn = 60t - t2 (2)
a„ = — 2 m/s2
Os móveis voltarão a se encontrar quando ocuparem a mesma posição
cm relação ao referencial adotado.
Logo, o encontro ocorrerá quando SA— S„ (3).

119. % w e m d & a S ~ 1 2 1
Assim, substituindo (1) c (2) cm (3), vem:
2 0 t 4 - — t2 = 60t — t2
3
(4 ,- 4o
)=°
- t2 — 40t = 0 =>
I) t = 0 s (instante inicial).
5
II) t —40 = 0
3
120
t = ------- = t = 24 s
Resposta: alternativa b.
4 . MAPOFEI — A velocidade de um carro, em função do tempo,
pode ser descrita pelo gráfico a seguir.
Quanto andou o carro du­
rante os primeiros cinco se­
gundos? Quanto andou du­
rante os vinte segundos?
Qual a velocidade média do
movimento?
Resolução:
• Como o movimento é descrito num único sentido (velocidade es­
calar positiva), podemos dizer que a distância percorrida pelo carro
coincide com o deslocamento AS.
Assim, durante os primeiros cinco segundos de movimento teremos:
A S (0 i H i í i : A to » H 3 *> -----^ 5 *» — -}'
5 . 20
•iSfii, h í «i -*-50 m
Para o tempo tota! de movimento vem:
__ 2 0 -f 1 0
-h.’iííi =A(o, h -
‘o•>•
—> AS<o*h 20»j = H
------------• 20
ASÍ(>, h 2 <
ik» - +300 m
• Lembrando que V„
AS
At
-, então:
y = -}-
(0 *H2 0 »
>
300
20
V ° = 1 5 m , S
Resposta: O móvel andou 50 m durante os primeiros 5 s; 300 m durante
os 20 s e sua velocidade média nos 20 s dc movimento foi de 15 m/s.

120. 122
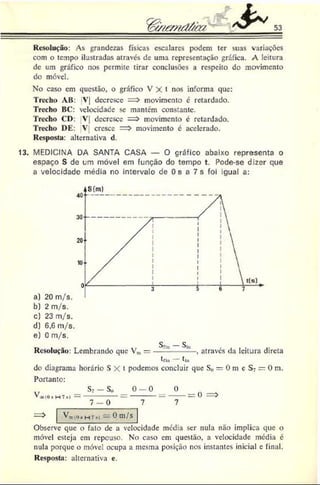
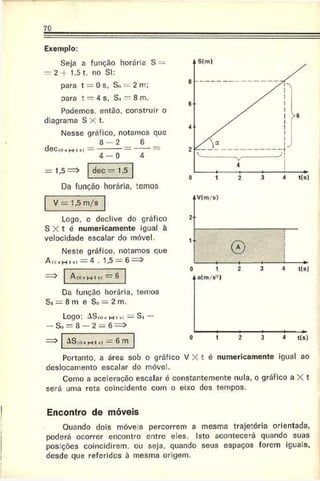
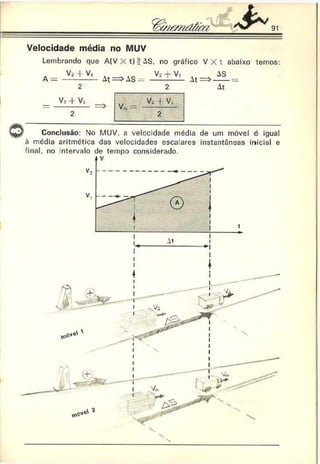
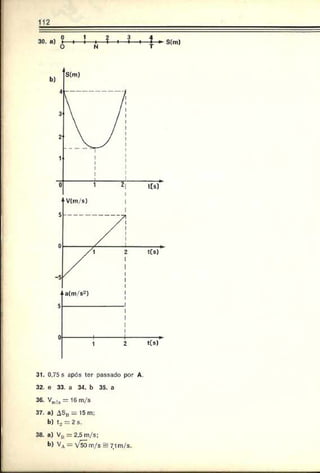
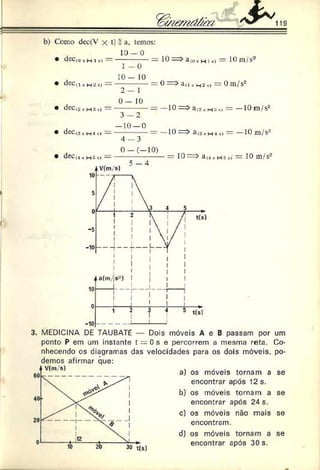
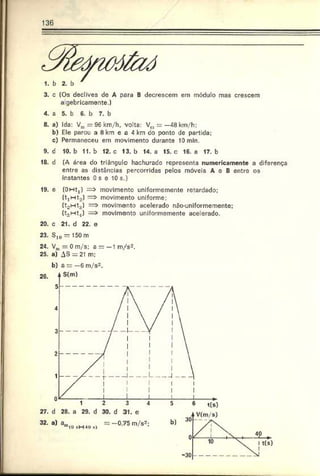
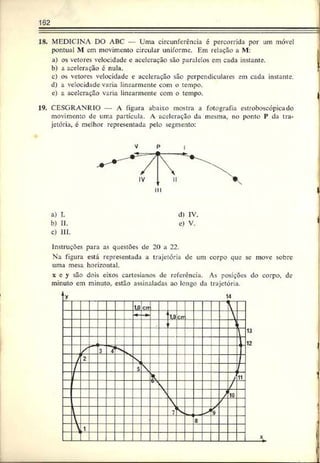
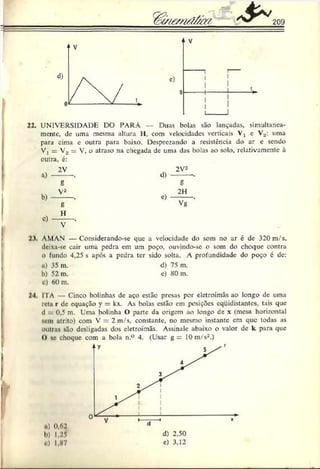
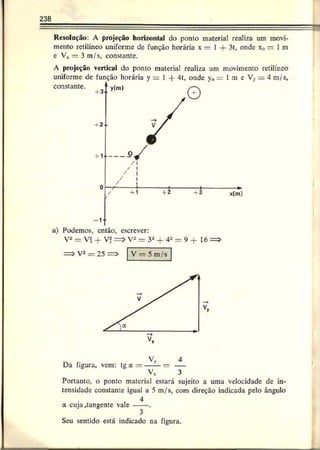
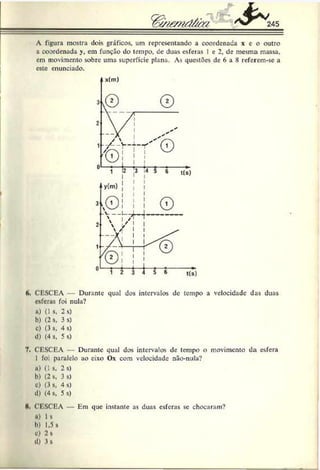
5. ENGENHARIA DE SÃO CARLOS — Dois carros viajam no mesmo
sentido em uma estrada retilínea. No instante em que um está
ultrapassando o outro, os deis motoristas percebem um perigo à
frente e freiam simultaneamente. O gráfico da figura mostra a
variação da velocidade dos dois com o tempo. Pede-se a distância
entre os dois carros no instante em que suas velocidades forem
iguais.
a) 20 m
b) 10 m
c) 50 m
d) 15 m
e) 25 m
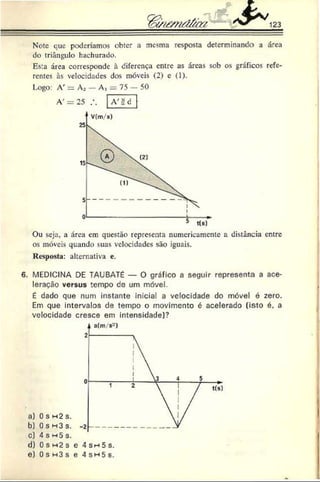
Resolução: As velocidades dos móveis sc igualam no instante 5 s, con­
forme podemos deduza- do gráfico.
|t = 0 s| E Z H ] t = 5s
(1 )
v^
• (2 )
AS,
AS.
Observando o esquema anterior,
podemos escrever:
d = AS2 -A S , (1),
onde AS2 = A-
2 e AS, ^ A,.
i c 25 + 5
Logo, ASj = ------------ . 5 =: 75 m
e AS,
15 + 5
. 5 = 50 m.
Portanto, voltando a (I), vem:
d — 75 — 50 fd = 25 m

121. 123
Note eue poderíamos obter a mesma resposta determinando a área
do triângulo hachurado.
Es:a área corresponde à diferença entre as áreas sob os gráficos refe­
rentes às velocidades dos móveis (2 ) e (1 ).
Logo: A' = A2 — Ai = 75 -
A '= 25 [717
50
Ou seja, a área em questão representa numericamente a distância entre
os móveis quando suas velocidades são iguais.
Resposta: altern ativ a e.
6. MEDICINA DE TAUBATÉ — O gráfico a seguir representa a ace­
leração versus tempo de um móvel.
É dado que num instante inicial a velocidade do móvel é zero.
Em que intervalos de tempo o movimento é acelerado (isto é, a
velocidade cresce em intensidade)?
d) 0 s m 2 s e 4 Sm 5 s.
e) 0 s h 3 s e 4 s h 5 s .
L

122. 124
Resolução: No gráfico a — f(t) a área sob a curva representa numerica­
mente a variação de velocidade do móvel. As áreas acima do eixo f
estão associadas a variações positivas de velocidade, e as áreas abaixo
do eixo t. as variações negativas de velocidade.
4 a(m/s~)
Lembrando que o corpo partiu do repouso, até o instante 3 s a velo­
cidade do móvel crescerá tanto algebricamentc como em módulo.
Do instante 3 s ao instante 5 s leremos uma variação negativa de velo­
cidade, o que significa uma redução no valor algébrico da velocidade.
Determinemos os valores numéricos das velocidades:
Os h I s: A(0 , h i ,i = 1 • 2 = 2 = > Vl - V0 = 2 = *
= > V, — 0 = 2 = > V, = 2 m/s
1 s h 2 s: A,i , h s .i = 1 . 2 = 2 = > V* —V! = 2 =>
= > V2 — 2 = 2 = > V2 = 4 m/s
1 . 2
2 s m 3 s : A (2 h h s ■
> = ------------- = 1 = > V3 — V2 = 1 = >
2
= > V* —4 = 1 = > V3 = 5 m/s
1 . 2 /-v
3 SH4 s: A(a*H4 8i = —-----= 1 = > V4 — V3 = (—
) 1
==> V, - 5 = - 1 = > V4 = 4 m/s
1 2
4 s w5 s: A(4 ■Hs •) = — -— = 1 = > V5 — V4 = Q 1 =>
= > Vs — 4 = —1 = > V5 = 3 m/s
Resumindo: o movimento foi progressivo durante todo o intervalo de
tempo cbnsiderado, sendo acelerado de 0 s a 3 s c retardado de 3 s a 5 s.
Resposta: alternativa b.

123. Enunciado para as questões 1 c 2:
Nos gráficos a seguir são representadas as distâncias x à origem da trajetória
retilínea, em função do tempo t, de uma partícula em movimento:
1. FUNDAÇÃO CARl.OS CHAGAS — Em quais dos movimentos acima
representados a velocidade da partícula adquire o valor zero?
a) I e III. d) III e IV.
b) II c V. e) II c III.
c) I e IV.
2. FUNDAÇÃO CARl.OS CHAGAS — Em qual dos movimentos acima
representados a velocidade da partícula pode ter valores negativos?
u) I d) IV
b) II c) V
c) III

124. 126
3. UNIVERSIDADE DE BRASÍLIA — No gráfico abaixo, deslocamento
versus tempo de um corpo, podemos afirmar que sua velocidade
a) decresce de A para B e cresce
de B para C.
b) decresce de A para C.
c) cresce de A para C.
d) cresce de A para B e decres­
ce de B para C.
4. UNIVERSIDADE DE SÀO CARLOS — Qual dos gráficos abaixo melhor
representa o movimento de um móvel que vai desde um ponto A até um
ponto B, através de uma trajetória retilínea, com velocidade constante?
O enunciado c o gráfico que seguem se referem às questões de 5 a 7.
O gráfico descreve o movimento retilíneo de um carro.

125. 'S * 127
5. MEDICINA DE ITAJUBA — Em qual intervalo o movimento é retardado?
a) Os h IOs. d) 50sw60s.
b) 20sm40s. c) Em nenhum dos intervalos.
c) 40 s h 5 0 s .
6. MEDICINA DE ITAJUBÁ — No tempo t = 0s, a velocidade do carro
cra:
a) Om/s. d) 3,0 m/s.
b) 1,0m/s. e) 4,0 m/s.
c) 2,0 m/s.
7. MEDICINA DE ITAJUBÁ — No intervalo 0s a 20s, a velocidade média
do carro foi igual a:
a) 0 m/s. d) 3,0 m/s.
b) 1,0m/s. e) Nenhuma das respostas anteriores.
c) 2,0 m/s.
H
. INATEL — O gráfico da figura abaixo representa o movimento dc um
automóvel durante 20 minutos de percurso reto. Pergunta-se:
a) Qual a velocidade média do automóvel na ida e qual a velocidade média
do automóvel na volta, em km/h?
b) A quantos quilómetros do ponto dc partida cie parou?
c) Quanto tempo o carro permaneceu cm movimento?
*
>
. FUVEST — Dois pontos móveis P e Q percorrem um mesmo eixo Ox;
seus movimentos estão representados na figura que segue, pelo gráfico do
espaço x em função do tempo t.

126. 128
Podemos afirmar que:
a) P e O passam, no mesmo ins­
tante, pelo ponto de abscis­
sa x = 0 .
b) a aceleração de P é maior que
a de Q.
c) a velocidade de O é maior
que a de P.
d) P e Q passam, no mesmo ins­
tante. pelo ponto de abscis­
sa x = X|.
e) P e Q movcm-sc em sentidos
opostos.
10. FACULDADES FARIAS BRITO — O gráfico que segue mostra como
a velocidade de uma partícula varia com o tempo: T, c T, são duas
retas tangentes à curva nos pontos P; e P2, respectivamente. As acelera­
ções escalares instantâneas que a partícula apresenta nos instantes t, = 4 s
e U = 6 s são de:
T
,
b) — m/s2 eO m/s2.
2
d) 36m/s2 c 42 m/s2
.
II. FUNDAÇÃO CARLOS CHAGAS Qual dos gráficos da velocidade do
móvel em função do tempo pode representar um deslocamento de 6 m em 4 s?

127. 12. PUC (CAMPINAS) — No gráfico representa-se velocidade em função do
tempo:
a) O movimento tem um só sentido com velocidade variável.
b) O gráfico está errado, pois não se representa velocidade negativa.
c) O móvel percorreu 3 m e, cm seguida, parou bruscamente; fez percurso
igual cm sentido contrário e parou no ponto de partida.
d) Do gráfico apresentado só podemos obter velocidade e aceleração do
móvel em função do tempo.
C
) Nenhuma das respostas anteriores.
13. FATEC — L'ma partícula percorre um eixo Ox com velocidade que segue o
diagrama abaixo:
V(m/s)
(1) Entre as datas Ose 2 s o per­
curso mede 8 m.
(2) Entre as datas 0 s e 4 s o per­
curso resultante é nulo.
(3) Entre as datas 2 s e 4 s (ex­
clusive) a aceleração é de
■♦•4,0m/s1
23
.
a) Somente (I) c correta.
b) (1) c (3) são corretas.
c) Todas as afirmações são corretas.
d) Nenhuma das afirmações c correta,
c) Resposta diferente das anteriores.

128. 130
14. UNIVERSIDADE DE SANTA CATARINA — Do gráfico V x t relativo
ao movimento de uma partícula, mostrado na figura, podemos concluir que.
entre t = Os e t = 3s. o espaço por ela percorrido c igual a:
a) 10m.
b) 12 m.
c) 7 m.
d) 4 m.
e) 5 m.
15. UNIVERSIDADE DE MINAS GERAIS — O gráfico que segue representa
a velocidade cm função do tempo de uma partícula que se desloca cm linha
reta.
Quanto ao deslocamento da par­
tícula, a afirmação certa é:
a) Seu deslocamento total (entre
0 s e 6 s) é diferente de zero.
b) O deslocamento da partícula
entre 0 s c ls c igual ao des-
' locamento entre 3 $ e 4 s.
c) O módulo do deslocamento
entre 0 s e ls c igual uo mó­
dulo do deslocamento entre
5 s e 6 s.
d) O módulo do deslocamento sempre cresce com o tempo,
c) O módulo do deslocamento sempre decresce com o tempo.
16. FEI — Um móvel tem velocidade escalar variável com o tempo conforme
o gráfico abaixo. Assinale a afirmação correta:
b) A distância percorrida pelo móvel nos primeiros 10 segundos de movi­
mento é de 20 m.

129. c) A aceleração do móvel é negativa no intervalo de tempo 6sw8 s.
d) O móvel está em repouso no intervalo de tempo 4 s h 6 s.
e) O móvel tem movimento retardado entre os instantes t ^ 2 s e t = 4 s.
17. FUVEST — Um automóvel faz uma viagem em seis horas c sua velocidade
varia em função do tempo, aproximadamente, como mostra o gráfico a
seguir.
A velocidade média do automóvel na viagem é dc:
______________________________________________ ’fé v tm M tá m /& * * * 131
b) 40km/h. e) 50km/h.
c) 45 km/h.
IH. UNIVERSIDADE DE SANTA CATARINA — No gráfico das velocida­
des dos móveis A e B. o triângulo hachurado representa:
a) a diferença entre as acelerações dos
móveis.
b) a soma das distâncias percorridas
pelos móveis.
c) a diferença entre as velocidades
dos móveis.
d) a diferença entre as distâncias per­
corridas pelos móveis.
e) uma grandeza sem nenhum signifi­
cado físico.
19. MACKENZIE — Um móvel descreve uma reta. com velocidade que varia
Nessas condições, podemos afirmar
que:
a) no intervalo (0. t,) o móvel se des­
locou com aceleração variável.
b) no intervalo (t,. t2) o móvel esteve
parado.
c) no intervalo (t2, t3) o movimento
foi uniformemente acelerado.
d) no intervalo (t3, t4) a velocidade do móvel permaneceu constante,
c) Nenhuma das afirmações c correta.

130. 132
20. ACAFE (SANTA CATARINA) — O gráfico representa a intensidade da
velocidade cm função do tempo de uma partícula que se desloca numa tra­
jetória retilínea.
Com base no gráfico, a alternativa correta c:
a) As acelerações da partícula nos intervalos de tempo 0 s a 5 s c 2 0 s a 2 5 s
são diferentes.
b) A partícula esteve cm repouso no intervalo de 5 s a 10s.
c) De 0 s a 5 s a distância percorrida foi de 75 m.
d) No intervalo dc 15 s a 20 s o movimento é retilíneo uniforme,
c) A aceleração da partícula dc 10 s a 15 s foi de 4 m/s2.
As explicações a seguir referem-se às questões 21 e 22.
Três partículas partem da origem com velocidades cujas equações horárias
são representadas a seguir:
21. MEDICINA DO ABC — Considerando as partículas em ordem decrescente
quanto à distância em relação à origem, ao fim de vinte segundos elas esta­
rão dispostas da seguinte maneira:
a) I, II, III. d) II, III, I.
b) I, III, II. e) III, II, I.
c) II, I, III.

131. 22. MEDICINA DO ABC — Qual a partícula que tem gráfico de aceleração
satisfazendo aos valores e ao aspecto a seguir?
aím/s“)
1
I
I
I
2õ ti?)
d) I c III.
e) Nenhuma.
c) III.
23. FEI — O gráfico dado define a velocidade dc um ponto em função do
tempo.
A posição inicial do ponto c dada por S0 —50 m.
Qual a posição do ponto no instante t 10 s?
24. FATEC — O diagrama ao lado
dá a velocidade de um ponto em
função do tempo. Para o inter­
valo dc tempo entre as datas
0« c I0,0s, determinar a velo­
cidade media c a aceleração.
25. INATEI. — O gráfico abaixo representa a variação da velocidade cm fun­
ção do tempo, para um ponto P movendo-se cm linha reta. Pedem-se:
a) a distância total percorrida.
b) a aceleração no intervalo de tempo entre 4 e 5 segundos.
V(m/s)
5 Us)
a) I.
b) II.

132. 134
26. IME — Do movimento de uma partícula c dado o diagrama V x t. Trace
o diagrama S X t, sabendo que para t = 0 s, S = 0 m (S = espaço).
-1
-2
-3
-4
V(m/s)
t(s)
27. FEI — Ura móvel cm trajetória retilínea tem um movimento cuja veloci­
dade varia com o tempo conforme o gráfico abaixo:
Quanto à sua aceleração, podemos afirmar que:
a) c negativa entre Os c 2 s.
b) c positiva entre 2 s c 6 s.
c) é positiva de 6 s a 9 s.
d) é positiva de 9sa 12s.
e) c positiva dc 6 s a 7,5 s e negativa de 7,5 s a 9 s.
28. FEI — Em relação à questão anterior, quanto ao movimento do móvel,
podemos afirmar que:
a) c retardado no intervalo dc 9 s a 12 s.
b) é retardado no intervalo dc 8 sa 9 s.
c) é acelerado no intervalo de 6 s a 7 s.
d) é uniformemente acelerado no intervalo de 2 s a 6 s.
e) é retardado no intervalo dc 0 s a 2 s.

133. Enunciado referente às duas questões seguintes:
Um móvel entra em movimento retilíneo a partir do repouso. O .gráfico de
sua aceleração cm função do tempo decorrido a partir do instante de partida
é dado pela figura seguinte:
29. CESCEA — Depois de 8 s, sua velocidade será igual a:
a) 12 m/s. d) 16 m/s.
b) Om/s. e) Nenhuma das anteriores.
c) 22 m/s.
30. CESCEA — Em que trecho a velocidade do corpo diminuí com o tempo?
a) No trecho AB.
b) No trecho CD.
c) No trecho BC.
d) Nunca.
e) Nenhuma das respostas anteriores e correta.
31. PUC (SÀO PAULO) — Sobre um corpo inicialmente em repouso atua uma
aceleração que varia com o tempo, de acordo com o diagrama abaixo:
A velocidade adquirida pelo
corpo c máxima no instante t
igual a:
a) 5 s.
b) 15 s.
c) 20 s.
d) 25 s.
c) 10 s.
32. FEI — O gráfico da aceleração de um móvel em movimento retilíneo cm
função do tempo c dado na figura. Determinar:
1
i
i
’? 40 t(s)
a) a aceleração média no inter­
valo 0 sh 40s.
b) o gráfico- da velocidade em
função do tempo. Sabe-se
que a velocidade inicial é
nula.

134. 136
3. c (Os declives de A para B decrescem em módulo mas crescem
a gebricamente.)
4. a 5. b 6. b 7. b
8. a) Ida: VIH= 96 km/h. volta: Vm= -4 8 km/h;
b ) Ele parou a 8 km e a 4 km do ponto dc partida;
c) Permaneceu em movimento durante 10 min.
9. d 10. b 11. b 12. c 13. b 14. a 15. c 1G. a 17. b
18. d (A área do triângulo hachurado representa numericamente a diferença
entre as distâncias percorridas pelos móveis A e B entre os
instantes 0 s e 10 s.)
19. c (0H t1) = $ movimento uniformemento retardado;
(t,M to) = > movimento uniforme:
(toMt3) => movimento acelerado não-uniformemente;
=> movimento uniformemente ace erado.
20. c 21. d 22. e
23. SJ0 — 150 m
24. VJr = 0 m/s; a = —1m/s2.
25. a) AS = 21 m;
b) a = —6 m/s2.

136. Vetor
Dado um segmento orientado de reta AB, podemos distinguir
nele três características:
• direção: a mesma da reta à qual pertence:
• sentido: de A para B;
• módulo: é o valor numérico associado ao comprimento do seg­
mento de reta.
Dois segmentos orientados são ditos eqüipolentes quando pos­
suem a mesma medida, a mesma direção e o mesmo sentido.

137. j ~ 139
• Conceito de vetor — Tomemos um conjunto de segmentos orien­
tados. eqüipolentes. AB. CD. EF e GH. Tais segmentos apresentam,
em comum, a mesma associação: módulo-direçãosentido. Esta asso­
ciação abstrata é denominada vetor.
Resumindo:
módulo
Vetor : direção
i sentido
Observe que
8
ficamente, o mesmo vetor, simbolizado por V. Isto se deve ao fato
de que todos os segmentos eqüipolentes têm a mesma direção, o
mesmo sentido e o mesmo módulo.
é fá iw a ttiC L
O símbolo V representa um vetor e não deve ser substituído por um
número Quando queremos ropresentar apenas o medulo do vetor V.
—
♦
usamos o símbolo V . Assim, se um vetor V tem módulo 5. devemos
oscrcvor |V —5 e não V = 5.
Os vetores estão sempre associados às grandezas vetoriais.
Grandezas vetoriais são grandezas físicas que, para ficarem perfeita­
mente caracterizadas, necessitam de intensidade, direção e sentido.
Por intensidade se entende módulo seguido de unidade.
Resumo:
Grandeza vetorial
intensidade (módulo -r unidade)
<direção
sentido
Exemplos de grandezas físicas vetoriais: força, velocidade, acele­
ração. etc.

138. 140
• Adição de vetores — Dados os vetores Vi, Va. V3 e V*. o vetor-
-soma S é obtido traçando-se, a partir de uma origem O arbitraria-
mente escolhida, os segmentos orientados representativos dos ve­
tores. de modo que a extremidade de um coincida com a origem do
seguinte e assim por diante.
O vetor-soma S é representado pelo segmento orientado de ori­
gem em O e extremidade coincidente com a extremidade P do seg­
mento representativo do último vetor.
Importante: a adição de vetores é comutativa, isto é. qualquer que
seja a ordem dos vetores-parcela, o vetor-soma será sempre o mesmo.
• Produto de um número real por um vetor — Dados um número
—
> —
> —
>
real n e um vetor V. o produto n . V é um vetor U. com as seguintes
características:
módulo: U = n| . V ;
direção: a mesma de V se n ?! 0.
— — >
sentido: se n > 0. U e V têm sentidos concordantes;
—
>
■ —
>
se n < 0. U e V têm sentidos opostos.

139. 141
Exemplos:
U = +2V
ffló a w a p feà -
1) Quando n = —1, teremos U = —V. Neste caso. U é denominado
vetor-oposto ce V
. Observe o último exemplo acima.
Conclusão: O vetor-oposto (—V) tem a mesma direção e o mesmo
módulo de V. mas sontido contrário ao deste.
2) Caso particular: Quando n = 0. o vetor-produto U será nulo. ou seja.
0. ü = O.
• Vetor-diferença — O vetor-diferença D = Va —Vi pode ser ob-
— ► — ►
tido pela soma de Va com o oposto de Vj.

140. 142
• Decomposição de um vetor — Dado um vetor V. podemos de­
compô-lo segundo duas direções x e y ortogonais.
Assim.
Vx e V, são denominados
componentes de V segundo as
direções x e y.
Reciprocamente, conhecen­
do-se os vetores-cornponentcs
■
—
> —
>
Vx e Vv podemos determinar o
vetor V.
Vetor-posição
Quando a trajetória de um móvel não é conhecida, em lugar de
a posição ser medida através de um arco de trajetória (espaços),
—
►
será ceterminada através de um vetor-posição, representado por r.
de origem arbitrária O e extremidade na pos;ção P ocupada pelo móvel.

141. Vetor-deslocamento
Sc um móvel parte de uma posição Pi e chega a uma posição
P- após um intervalo de tempo At. diremos que ele realizou um deslo­
camento escalar AS e um deslocamento vetorial Ar.
Esse vetor-deslocamento Aí é. por definição, a diferença entre
o vetor-posição-final ríin e o vetor-posiçác-inicial rln.
Ou seja:
^
Ar — Tfm fia
Observe que numa trajetória curvilínea AÍ, < jAS’, enquanto que
numa trajetória retilínea A Í = AS|.
Ou seja: Ar ^ ASj

142. 144
Resumindo:
DESLOCAMENTO
Sendo o vetor-deslocamento Ar uma grandeza vetorial, além do módulo
do vetor a ela associado, a grandeza possui também uma unidade. A esse
conjunto (módulo -
+
■ unidade) chamamos de intensidade do vetor-
•deslocamento e representamos simplesmente por Ar.
Vetor-velocidade
• Vetor-velocidade-média — Seja um móvel que se desloca de Ar
num interva o de tempo At.
Denomina-se vetor-velocidade-média o quociente entre Ar c At.
Ou seja:
-> Ar
Vc, = -----
At

143. memd&a
Como |Ar' ^ |ASj, entáo Vr, ^ jV,„ .
Movimento curvilíneo: |V J < |Vm
•Movimento retilíneo: |V„, - Vn
Trajetória curvilinea
Trajetória retilínea
!
• Vetor-velocidade-instantânea — Quando o intervalo de tempo At
tende a zero, o vetor-velocidade-média tende ao vetor-velocidade-ins-
tantãnea.

144. 146
O vetor-velocidade-instantânea de um móvel possui a mesma in­
tensidade que a velocidade escalar instantânea, tendo direção tangente
à trajetória e sentido concordante com o sentido do movimento do
móvel.
Soltando-se o barbante, observamos que a bola segue a
reta tangente à curva no ponto.
O vetor-velocidade - instantânea índica o que o corpo tende a lazer
num dado instante seguir a reta tangente
Sendo o vetor-velocidade V uma grandeza vetorial, sua intensidade será
representada simplesmente por V.
Exemplos:
Na figura ao lado. note que:
—
>
• vetor-velocidade Vi
intensidade: Vi — 30 m/s:
direção: horizontal:
sentido: esquerda para a
direita.
—
>
• vetor-velocidade V2
intensidade: Va = 20 m/s;
direção: vertical:
sentido: de cima para baixo.
—
>
• vetor-velocidade Va
intensidade: V3 —
= >/l0= -- 202= V"500 =>
— 10 Z~
5 m/s:
direção: indicada pelo ângulo
1
a, cuja tangente é — ;
2
sentido: indicado na figura.

145. =
Vetor-aceleração
• Vetor-aceleração-tangencial — Conforme foi visto anteriormente,
a aceleração indica a taxa de variação da velocidade de um móvel
no tempo.
O vetor-aceleração-tangencial indica que a intensidade do vetor-
Movimento retardado
km/h j*- km/h
_ ° T _ _ _ _ _ _
________
Possui direção tangencial e sentido que depende do tipo de movi­
mento:
~ -> — >
• movimento acelerado: aT e V têm o mesmo sentido;
— > —■>
• movimento retardado: aT e V têm sentidos opostos.
A intensidade do vetor-aceleração-tancencial é igual à intensidade
da aceleração escalar.
Ou seja: fc l - 1
*
1
õfó& W tpâCL-------------------------------------------------------------------------------------------------------
Sendo o vetor-aceleração-tangencial a T uma grandeza vetorial, sua
intensidade será simplesmente representada por a T .
• Vetor-aceleração-centripeta — O vetor-aceleração-centrípeta in­
dica a taxa de variação da direção do vetor-velocidade no tempo.

146. 148
Possui direção normal à trajetória, tendo sentido orientado para o
centro da trajetória, no ponto considerado.
Verifica-se que a intensidade
é dada pela expressão
V-
ar —
ac) do vetor-aceieração-centripeta
, onde V é a intensidade da velo-
cidade do móvel e r é o raio da trajetória no ponto considerado.
• Vetor-aceleração-total — O vetor-aceleração-total é a soma ve­
torial dos vetores aceleração tangencial e aceleração centrípeta.
Ou seja:
—
>
Como a direção do vetor aT é ortogonal à direção do vetor ac
podemos escrever:
r® ~ aT — ar .
onde Y. aT e ac representam, respectivamente, as intensidades dos
vetores aceleração T i e Ç

147. J S h 149
ijJJJS Complementação: Façamos, agora, uma análise de f em todos
os tipos de movimento:
• MRU
MCU
• MRA
• MRR
I
• MCA
• MCR
retilíneo => ac — O
—
► -4
jniforme = > a-r — C
circular => ac ¥= O
—
> —
>
uniforme => aT = O
retilíneo => ac = O
—
> —
^
acelerado => O
- 4 —4
retilíneo => ac = O
—
> —
►
retardado => a-r O
—> - 4
circular => a
<
--/=O
—
4 —
>
acelerado => ar 7
*=O
— > — >
circular => ac / O
—
> —
>
retardado = >ax 7
*=O
• Vetor-aceleração-média — Seja um móvel que varia seu vetor-
•velocidade de 7 Jn a num intervalo de tempo At. Definimos como
vetor-aceleração-média do móvel neste intervalo de tempo o quo-
i

148. 150
1. FUNDAÇÃO CARLOS CHAGAS — Na figura que segue estão
— ► — >
desenhados dois segmentos X e Y. Estes segmentos representam
deslocamentos sucessivos de um corpo. Qual é a intensidade do
— > — >
deslocamento representado por X -f- Y? (A escala da figura é
1 : U
a) 4 cm
b) 5 cm
c) 8 cm
d) 13 cm
e) 25 cm
Resolução: Traçando-se o desloca-
mento A?—X -|- Y, podemos escre­
ver: ArL
>— 4" -|- 32 = I6 -- 9 =
= 25 =>
Determinemos a direção do deslo­
camento Ar.
Da figura, vem:
tg a = —— = 0,75 =>
4
=> tg a 0,75

149. Usando uma tabela trigonométrica (ver Pranchas Matemáticas) pode­
mos verificar que a ss 37°.
Assim, a direção do deslocamento Ar será indicada pelo ângulo
a ~ 37°.
Sentido de Ar: de O para P.
Resposta: alternativa b.
2. UNIVERSIDADE DE SANTA CATARINA — Uma pessoa sai de sua
casa e percorre as seguintes distâncias em qualquer ordem pos­
sível:
I) 30 metros para Leste.
II) 20 metros para o Norte.
III) 30 metros para Oeste.
No fina; das três caminhadas, a distância cm que ela se encontra
do ponto de partida é:
a) 80 m.
b) 50 m.
c) 20 m.
d) 40 m.
e) 60 m.
Resolução: Construindo a poligonal orientada, obteremos o esquema
seguinte: 73
Observamos, então, que:
Ar, = 30 m
Ar3 = 20 m
Ar.i = 30 m
onde Ar*= Ar, + Arò -f Ar-,.
Da figura, temos:
Ar — 20 m
Resposta: alternativa c.

150. 152
3. FUNDAÇÃO CARLOS CHAGAS — A velocidade vetorial média de
um corpo que parte de um ponto P, percorre o segmento de reta
PQ e volta, pelo mesmo caminho, à origem P. no intervalo de tem­
po At, é:
a) O.
b) OP/At.
d) 2PQ/A1.
e) PQ/At.
c) 2QP/At.
Re.solução: Como o corpo retorna ao ponto dc partida, teremos:
Ar = PO 4- OP = O
PQ
P *■
->
OP
Ar
Sendo V» —------, então Vm
Al
Ke.spo.sta: alternativa a.
H q.
O —
►
V', - o
At
O enunciado que segue refere-sc às questões de 4 a 6.
A figura mostra uma fotografia estroboscópica de uma bola que
se move ao longo da trajetória . . . . 1, 2, 3...........8, 9. 10............. 12,
13. 14. . . .
As regiões dc 1 a 4, 8 a 11 e 12 a 14 são linhas retas.
As regiões de 4 a 8 e de 11 a 12 são arcos de circunferências.
Os intervalos de tempo entre duas posições sucessivas da bola
são todos iguais.

151. 4. FEI — A velocidade instantânea da bola no ponto 6 é melhor re­
presentada por qual dos segmentos abaixo?
s)
Resolução: lembrando que o vetor-
-vclocidade é tangente à trajetória e
que o movimento é descrito da foto
(4) para a foto (8), podemos repre­
sentar a velocidade no ponto (6)
conforme o esquema ao lado.
Resposta: alternativa b.
5. FEI — A aceleração instantânea da bola no ponto 6 é melhor repre­
sentada por qual dos segmentos abaixo?
a) zero
b)
Resolução: De (4) a (8) o movi­
mento c uniforme; logo, V e cons-
—
> —
>
tante. Assim, ar = O.
Como a trajetória é curva, a acele­
ração é centrípeta
Logo, Y«= ac, sendo indicada conforme a figura anterior.
Resposta: alternativa e.

152. 154
6. FEI — A aceleração instantânea da bola no ponto 13 é melhor
representada por qual dos segmentos abaixo?
d)
e) zero
c) *
Resolução: Na região considerada,
a trajetória é retilínea. Assim, não
há aceleração centrípeta, pois a di­
reção da velocidade não varia.
—
> —
>
Logo, ac = O.
Como o movimento é acelerado, o
móvel somente possui aceleração
tangencial, ou seja, y™= ar. con­
forme a figura ao lado.
Resposta: alternativa b.
7. UNIVERSIDADE DE MINAS GERAIS — Um ventilador acaba de
ser desligado e está parando vagarosamente, girando no sentido
horário. A direção e o sentido de aceleração da pá do ventilador
no ponto P são melhor representados pela figura:
P

153. n e m d & tz ^ 155
Resolução: Devido ao movimento retardado, o ventilador terá acele­
ração tangencial de sentido contrário ao do movimento, além de ter
aceleração centrípeta, pois a velocidade varia em direção.
Portanto, a aceleração total do ponto P será y = a* — a<
;, conforme
indica a figura acima.
Resposta: alternativa d.
8. PUC (SÃO PAULO) — Um móvel parte do repouso e percorre
uma trajetória circular com raio de 100 m, assumindo um movi­
mento Lniformemente acelerado de aceleração igual a 1 m/s2 As
intensidades dos vetores componentes tangencial e normal da
aceleração valem, respectivamente, após 10 s:
a) 1 m/s2 e 10 m/s2.
b) 10 m/s2 e 1 m/s2.
c) 10 m/s2 e 10 m/s2.
d) 10 m/s2 e 100 m/s2.
e) 1 m/s2 e 1 m/s2.
Resolução: Como o movimento é uniformemente acelerado, podemos
escrever:
V = V„ -f at = > V = 0 -f 1 . 10 = > V = 10 m/s
Portanto:
• vetor-aceleração-tangencial a.,.
Sendo aT = a , vem
• vetor-aceleração-centrípeta a(.
V2 _ (IO)2 100
r
aT~ 1,0 m/s2
aò=
100 100
ac 1,0 m/s2
Resposta: alternativa c.

154. 156
9. FEI — A velocidade V? dc um móvel em função do tempo acha-se
representada pelo diagrama vetorial da figura. A intensidade da
velocidade inicial é Vo=20m/s.
t = Os
o
Esquematize a aceleração vetorial média e determine a sua inten
sidade entre os instantes t = 0 s e t = 8 s.
Resolução: Lembrando que y». =
então
Va - V, v 8 + (-V p)
8 - 0 “ 8
Podemos, então, construir o esquema abaixo, obtendo-se Y » 8-i
Observando o triângulo ABC, podemos escrever:
AC „ AC 20
------= sen 30° = > BC = ------------- => BC = --------
BC sen 30°
BC = 40
Portanto, AV 2 BC ==> AV ~ 40.
- * AV |AV
Sendo Y
m= ------, então ym — —
---- -
At At
40
onde Ymrepresenta a intensidade da aceleração vetorial média Y
m•

155. 1. FUNDAÇÃO CASPER LIBERO — Dois vetores são iguais quando:
a) têm a mesma intensidade.
b) são vctores-opostos.
c) têm a mesma direção.
d) têm o mesmo módulo, mesma direção e mesmo sentido.
2. FUNDAÇÀO CARLOS CHAGAS — A figura abaixo mostra três vetores
—
►—
> —
*
A. B c C. De acordo com esta figura, podemos afirmar que c verdadeira
a seguinte relação:
a) A + B + C = O
b) A = B - C
c) íT- A = C
d) A + B = C
e) A = íT-f C
3. EMESCAM (ESPÍRITO SANTO) — Sendo dados os vetores u e v da
figura, o segmento que melhor representa a diferença veforial d = u v é:
a) nulo c) c)
b) d)

156. 158
—
►—
♦
4. UNIVERSIDADE DE BRASÍLIA — Dados os vetores A. B C. I>, E.
F c G, representados geometricamente num plano, corno mostra a figura,
pode-se afirmar corretamente que:
b) D + A + B d) Nenhuma dessas.
5. FUNDAÇÃO CARLOS CHAGAS — Na figura seguinte está representada
uma parte de um mapa geográfico de uma região plana. 1 eZ são pontos
desta região. Qual das seguintes medidas mais se aproxima do valor da
distância entre os pontos Z e Y?
Z 100m
100m
a) 30C m
b) 400 rn
c) 500 m
d) 600 m
e) 700 m
6. MEDICINA DE POUSO ALEGRE — Uma pessoa sai para dar um pas­
seio pela cidade, fazendo o seguinte percurso: sai de casa e anda 2 quar­
teirões para o Norte; logo após, dobra à esquerda e anda mais 3 quarteirões
para Oeste, virando, a seguir, novamente à esquerda e andando mais 2
quarteirões para o Sul.
Sabendo que um quarteirão mede lOOm, o deslocamento da pessoa é de:
a) 700 m para Sudeste. d) 700 m em direções variadas.
b) 300 m para Oeste. e) zero.
c) 200 m para o Norte.

157. 7. I NIVI RSIDADE DE MINAS GERAIS — Um automóvel está sendo
testado em uma pista circular de 200 m de raio. Qua! será a intensidade do
vetor-desloeamento do automóvel após ter ele completado meia volta?
8. MEDICINA DE CATANDUVA — Em uma nave espacial há um compar­
timento semelhante a uma caixa de sapatos e cujas dimensões são iguais a
4 m X 3 m X 2 m. Sabendo que a mesma se encontra cm repouso em
rcluçBo a três estrelas fixas e livre da ação de campos gravitacionais. quer
se saber qual será a intensidade do vetor-deslocamento devido à movimen­
tarão dc um astronauta de um dos cantos do compartimento para o outro,
diamctralmente oposto, em busca dc uma ferramenta.
a) y'63 m
b) /29m
c) yXSni
d) Faltam dados para o cálculo.
c) Nenhuma das respostas anteriores.
9. MEDICINA DE SANTOS — Sejam Vu a velocidade escalar media e Vm
a velocidade vetorial média de um móvel num trecho dc sua trajetória.
Podemos dizer que:
c) Nenhuma das anteriores.
10. FUNDAÇÃO CARI.OS CHAGAS — A velocidade de um corpo c uma
grandeza vetorial, pois para determiná-la é preciso caracterizar sua direção:
a) c sentido.
b) sentido e intensidade.
c) sentido e ponto dc aplicação.
d) intensidade c unidade.
c) ponto de aplicação e unidade.
11. PUC (SÃO PAULO) - Sc a velocidade vetorial de um ponto material é
constante, sua trajetória:
a) é uma parábola.
b) pode ser uma reta. mas nào necessariamente.
c) deve ser uma reta.
d) é uma circunferência.
c) pode scr uma curva qualquer.
a) 628 m
b) 282 m
c) 2Q0 m
d) 400 m
e) 314 m
b) |Vm
| = |VJ.
O |Vm|$> VJ.
d) Vm= Vm
.

158. 160
12. CESGRANRIO — Uma partícula descreve, com movimento uniforme, urna
trajetória circular, representada na figura, no sentido indicado pela seta.
Entre as passagens A c II. a variação da velocidade vetorial da partícula
será melhor representada por:
B
13, FUNDAÇÃO CARLOS CHAGAS Um ponto em movimento circular
uniforme percorre um arco de círculo de raio R 20 cm e ângulo central
de 60° em 5 s.
A variação V., é, cm cm/s, igual a:
a)
10r
3
e)
4tt
3
d) 5v.
e) um valor diferente dos an­
teriores.
14. UNIVERSIDADE DE SANTA CATARINA — Uma partícula não possui
aceleração. Então, podemos concluir que:
a) sua velocidade é nula. :
b) ela está em movimento circular uniforme. )
c) ela está em repouso ou em movimento retilíneo uniforhie. '
d) a intensidade de sua velocidade é constante c sua direção variável.
e) a intensidade dc sua velocidade é variável e sua direção constante.

159. 15. UNIVERSIDADE DE SANTA CATARINA — No movimento circular
uniforme 6:
ii) variável a velocidade escalar e nula a aceleração centrípeta.
b) constante a velocidade escalar e r.ula a aceleração vetorial.
c) constante a velocidade escalar c constante a aceleração tangencial.
d) constante a velocidade escalar e nula a aceleração tangencial.
c) variável a velocidade escalar c constante a aceleração centrípeta.
16. UNIVERSIDADE DO ESPÍRI­
TO SANTO — Um corpo está
com movimento circular,unifor­
me. com sentido de 1 para 2.
Quando ele atinge o ponto A. o
par de vetores velocidade e ace­
leração representativo do movi-
mento será:
V
d)
“) _ *
.2.
V
h)
t,>
c)
V
c)
17. MEDICINA DE ITAJUBÁ Uma partícula realiza um movimento cir-
culur uniforme. Se escolhemos o centro da circunferência como nosso rc-
ícrcncial e chamamos de 1
* o vetor-posição da partícula num instante t
—
►
qualquer, de a o vetor-aceleração da partícula e de V a sua velocidade, qual
dentre as opções seguintes melhor representa a disposição dos três vetores
num mesmo instante t?

160. 162
18. MEDICINA DO ABC — Uma circunferência é percorrida por um móvel
pontual M cm movimento circular uniforme. Em relação a M:
a) os vetores velocidade c aceleração são paralelos em cada instante.
b) a aceleração é nula.
c) os vetores velocidade e aceleração são perpendiculares em cada instante.
d) a velocidade varia linearmente com o tempo.
e) a aceleração varia linearmente com o tempo. |
19. CESGRANKIO A figura abaixo mostra a fotografia cstroboscópicado
movimento de uma partícula. A aceleração da mesma, no ponto P da tra­
jetória, é melhor representada pelo segmento:
V p i
a) I. d) IV.
b) II. e) V.
c) III.
Instruções para as questões de 20 a 22.
Na figura está representada a trajetória de um corpo que sc move sobre
uma mesa horizontal.
x e y são dois eixos cartesianos de referencia. As posições do corpo, dc
minuto em minuto, estão assinaladas ao longo da trajetória.

161. 163
20. FUNDAÇÃO CARLOS CHAGAS — Entre os pontos 1 c 5 da trajetória,
qua. é a posição mais próxima daquela na qual foi nulo o vetor-componente,
na direção y, da velocidade vetorial instantânea do corpo?
a) I d) 4
b) 2 e) 5
c) 3
21. FUNDAÇÃO CARLOS CHAGAS Qual dos seguintes segmentos melhor
representa o vetor aceleração-instantânea do corpo na posição 8, conside­
rando que entre os pontos 7 e 9 o corpo tinha uma velocidade escalar
constante?
/y/mdába
22. FUNDAÇÃO CARLOS CHAGAS — Qual foi, aproximadamente, a inten­
sidade da velocidade vetorial media do corpo entre as posições 1 c 14?
n) 0,41 cm/min d) 0,87 cm/min
h) 0,57 cm/min e) 1,47 cm/min
c) 0,65 cm/min
23. FUVEST — Um menino está num carrossel que gira cohi velocidade an­
gular constante, executando uma volta completa a cada 10s. A criança
mantém, relativamente ao carrossel, uma posição fixa a 2 in do eixo de
rotação.
a) Numa circunferência representando a trajetória circular do menino,
—
► —
*
assinale os vetores velocidade V e aceleração a correspondentes a uma
posição arbitrária do menino.
— ► — *
b) Calcule as intensidades de V e de a.

162. 164
24. FEI — O vetor-velccidadc cie uma partícula, em função do tempo, está
representado na figura. Calcular as acelerações médias nos intervalos de
tempo I S h 2 s c 5 s -<6 s , indicando também sua direção c sentido.
Os 1s 2s 3s 4s
d 8. b 9. c 10. b
11. b (Se V é constante e não-nula =
=
> trajetória retilíneo; se V é
constantemente nula => trajetória é um ponto.)
12. b 13. c 14. c 15. d 16. c 17. e 18. c 19. b 20. c 21. a 22. d
bj V ss 1.3m/s;
a sr 0,8 m/s2.
( Intensidade: 15 m/s2
direção: horizontal
sentido: da esquerda para a direita
Intensidade: 15 m/s2
direção: vertical
sentido: de cima para baixo
2 4 .
“ ( S s h i i í :
1. d 2. e 3. e 4. c 5. c 6. b 7.

163. CffllUD
6

164. 166
Introdução
Seja um móvel que descreve
de origem 0 e raio r.
Deslocamento angular
uma trajetória circular orientada
Num instante t, seja P a po­
sição ocupada pelo móvel.
O ângulo central $ corres­
pondente ao arco OP é o ângulo
de fase do móvel nesse instante.
A medida algébrica de OP é S
(espaço do móvel no instante t).
Em radianos. temos:
Deslocamento angular do móvel
no intervalo de tempo At = t' — t
é. por definição, o ângulo central
A
<
I>= dV— <
í>
, onde 4>'éo ângulo
de fase no instante t e (IJ é o ân­
gulo de fase no instante t.
O ângulo central A
<
I> (deslo­
camento angular) corresponde
ao arco AS (deslocamento es­
calar).
Em radianos, temos:

165. Velocidade angular
Velocidade angular média é o quociente entre o deslocamento
angular A
<
1
>e o correspondente intervalo de tempo At.
Ou seja:
A
<
t>
0)M= -----
At
Sendo A
<
I>medido em rad e At medido em s. então co será medido
em r a d / s .
A velocidade angular instantânea é o limite da velocidade argjlar
média quando o intervalo de tempo tender a zero.
O sentido do movimento concorda com
o sentido da trajetória orientada.
-
O sentido do movimento discorda do
sentido da trajetória orientada

166. 168
Aplicações O estudo da velocidade angjlar é importante na
análise de movimentos circulares uniformes, quando estamos interes­
sados na rotação de sólidos.

167. Aceleração angular
Quando a hélice de um helicóptero é ligada, sua velocidade an­
gular aumenta até atingir seu regime normal de funcionamento. Di­
remos, então, que a hél:ce está dotada de uma aceleração angular.
Define-se aceleração angu­
lar média como o quociente
entre a variação da velocidade
angular i a e o correspondente
intervalo de tempo At.
Ou seja:
Ao>
«m = -----
At
Portanto:
Sendo Aw medido em rad/s e At medido em s. então x será me­
dido em rad/s".
A aceleração angular instantânea é o limite da aceleração angular
média quando o intervalo de tempo tender a zero.
Ou seja: x = lirn
ât-* o
Sinais de x:
a > 0 => c
«
> cresce algebricamente;
x < ü => o
> decresce algebricamente.

168. 170
Relação entre elementos lineares e angulares
Sendo S, V e a os elementos lineares do movimento de Lm móvel
em trajetória circular de raio r. e «
1
»
. to e a os elementos angulares
correspondentes, podemos escrever:
elemento angular —
elemento linear
raio
Ou seja:
s V a
(0 — —• a —
r r r
Na figura ao lado temos o
diagrama referente às velocida­
des lineares dos pontos de um
disco em movimento de rotação,
V
pois co— — => V —cor (V é
r
função linear do raio r quando co
é constante).
Movimento circular uniforme
No MU temos S — So -f Vt.
Num MCU de raio r, temos:
r r r
=> : — <
l>
o+ cot
Essa expressão é a função
horária angular do MCU. Observe
V
que co = — = constante 0.
r

169. O intervalo de tempo neces­
sário para que um móvel em
MCU dê uma volta completa é
denominado período (T).
O número de voltas dadas
por um móvel em MCU. num in­
tervalo de tempo, é denominado
freqüência (f).
Observe que
O período T é medido em s
e a freqüência f em s 1 ou hertz
(Hz). É usual a unidade rotação
por minuto (rpm) para freqüên­
cia.
Note que 1 rpm — -----Hz.
60
Nurh MCU, lembrando que
A
<
J>
o) = -----. quando A
<
J>= 2n rad
At
(1 volta), então At — T (período).
Logo:
Assim, por exemplo, lembrando que a Terra em seu movimento
de rotação leva 24 horas para completar uma volta, podemos deter-
2;i
minar a correspondente velocidade angular, ou seja. c>r -----—
2r .
24
( ! ) —
TC
12
rad/h.
i*

170. 172
v-
Lembrando que a<
: = -----, vem:
r
(wr)-
ac = -------- e dai
r
& ó& rxz#2a.___________
No MCI), como a velocidade escalar 6 constante, a intensidade do vetor-
-velocidade também é constante e a aceleração tangencial é nula. isto é.
7 r = 0 .
Entretanto, embora a intensidade do vetor-velocidade seja constante, sua
direção varia e a aceleração centrípeta é não-nula. isto é, ac O
t
MCU
ï = * r + «c
Como ar - O,
V-'
a(. = ----- = o)*r
r
v —a . onde
Movimento circular uniformemente variado
Lembrando que num MUV:
S = Su + Vot + — at2
2
V = V«, + at
V2= Vo + 2aAS
para um MCUV de raio r vem:
_S_ _So_ Vo t
r r r
1
2
t2
V
r
v-
-2
Vu a
-------1
-------t
r r
Vf 2aAS
-----+ ----------

171. & 173
Em decorrência do que foi exposto anteriormente:
<
1> —<!>„— to,t * f--------at*
2
d» = o)í, -f- 2t
'/)' = -f 2aA<í>
a
Observe que a = -----=
r
constante ^ 0.
(M & VO 0&2_____________________________________________________-
No MCUV tanto a Intensidade quanto a direção do vetor-velocidade vadam.
Logo. as acelerações tangencial e centrípeta são não-nulas
Sistema de transmissão
Em qualquer sistema de transmissão, as velocidades lineares
dos pontos em contato direto ou indireto (através de correia ou cor­
rente) são iguais em intensidade, admitindo não haver escorrega­
mento.
1) Observe o dispositivo ilustrado:

172. 174
Esquematicamente, teremos:
V,
Assim, para duas engrenagens em contato teremos:
V: = V3 w » ri = «fers = > 2 rc fin = 2 n f2rs ==> firi = f«ra
Portanto, quanto menor o raio da engrenagem, maior sua fre-
qüência de rotação.
J
♦
■ 9
I
2) Observe o dispositivo ilustrado:
Esquematicamente, teremos:
Admitindo que não haja escorregamento e que a corrente esteja
esticada, vem:
Vi — Ví => o):n = o)jrs => 2~ firi = 2^f3r2=>

173. 1. F-NGENHARIA DE SANTOS — Toma-se sobre uma circunferência
cie raio r = 2m um arco cie comprimento 5m. O ângulo central
correspondente é:
a) 0.40 rad.
b) 2,5 rad.
c) 3.0 rad.
d) t
: rad.
e) Nenhuma das respostas anteriores.
Resolução: Lembrando a expressão
da medida dc um ângulo em ra-
dianos, vem:
A
<
I>
AS
r
= > A
<
t>—
=> | A
<
I>= 2,5 rãd~
Resposta: alternativa b.
2. UNIVERSIDADE DE PERNAMBUCO — A velocidade angular do
ponteiro dos segundos dc um relógio vale. em rad/s:
a) 2n.
b) n.
d)
t
:
50
C) e)
»
u
15
Resolução: O período dc rotação do ponteiro dos segundos é T — 60 s
(tempo que c!c leva para completar uma volta).
Assim sendo, como w = - 2-~, vem:
T
2~
o» ----
60
d) rad/s
30
Resposta: alternativa c.

174. 176
3. CESCEA — Uma barra gira em torno do ponto O com velocidade
angular constante, completando uma volta a cada segundo. A ve­
locidade escalar de um ponto P da barra, distando 2 m do ponto
O, é:
a) 4r: m /s.
b) r . m /s.
n
c) -----m/s.
2
d) 8 r. m/s.
e) Nenhuma das anteriores.
Resolução: Do enunciado, te-
. . volta
mos: f = 1---------= 1 Hz.
Como o) — 2 r.f. vem:
o>= 2n . 1 = > o) = 2t
trad/s
Lembrando que VP = ü>rP,
concluímos que
Vp = 27:. 2 n=>|Vi» = A r. m/s
Resposta: alternativa a.
4. FEI — Um móvel se desloca em uma trajetória circu'ar, de raio
r = 2,00 m, obedecendo à lei horária S = 2,00 - 5,00t (SI).
No instante t = 10 s, a intensidade de sua aceleração resultante,
a intensidade de sua velocidade e a sua posição angular valem,
respectivamente:
a) 0.00 m /s2;5,00 m/s e —24,0 rad.
b) 12,5 m /s2;5,00 m/s e —48.0 rad.
c) 12,5 m /s2;5,00 m /s e —24,0 rad.
d) 5.00 m /s2;2.00 m /s e —24.0 rad.
e) 12.5 m /s2;2,00 m /s e —48,0 rad.
Resolução: Inicialmente, escrevemos a função horária do movimento
na forma angular.
S
Sendo S = 2,00 — 5,00 t e lembtando que O = — , então:
r
S 2,00 5,00 t 2,00 5.00
— = --------------- ----- t= *< I> = —---------------— t = >
r r r 2,00 2,00
=><!> = 1 ,0 0 -2 ,50t

175. V
• Assim, como para MCU <
í>= <
I>
0-j o)t, então <
I»
0= 1,(K) rad e to =
= —2,50 rad/s.
Para t = 10 s, <
J>
,0= 1 — 2,50 . 10 => — —24,0 rad
Como o movimento é circular e uniforme, a aceleração do móvel
6 a aceleração centrípeta.
Portanto, a<
- = o)-r = > ao = (—2,50)2 .2 = 6,25 . 2 = >
ao — 12,5 m/s2
Da função horária S = 2,00 — 5,00 t concluímos que:
V = —5,00 m/s.
Logo: !V| ^ 5,00 m/s
Kesposfa: alternativa c.
5. MEDICINA DE SANTOS — Sobre uma circunferência com 60 cm
do raio, dois pontos animados de movimento uniforme se encon­
tram a cada 30 s quando se movem no mesmo sentido, e a cada
10 s quando se movem em sentidos opostos. Determinar seus
períodos,
o) 10 s e 30 s.
b) 10 s e 20 s.
c) 15 s e 30 s.
d) 15 s e 20 s.
e) Nenhuma das respostas anteriores.
Kc.solução: Como o movimento dos pontos é uniforme, podemos es­
crever:
móvel (1): <
I>
, = <
I>
0j -f cM
móvel (2): <
I>
2= + wst

176. 178
Vamos adotar como origem das posições angulares o ponto P cm que
ocorrer um encontro qualquer. Neste instante, iniciamos o estudo dos
movimentos.
Assim, <
I>
o = <
I>
o = 0.
1 ' 2
Portanto: <
I>
: = Wit
<
&
a= w2t
1) Movimentos no mesmo sentido.
Ti T-. 30
2) Movimentos em sentidos contrários
Condição para o I,° encontro:
Logo:

177. Subtraindo (1) de (2), vem:
T , 10 30 30
Resposta: alternativa c.
6. UNIVERSIDADE DE MOGI DAS CRUZES — As duas polias A e B.
de raios rA e rR respectivamente (rA > rK), estão ligadas entre si
por uma correia C. Nestas condições, estando o sistema em movi­
mento, teremos:
a) A velocidade linear da polia A é maior do que a da polia B.
b) A velocidade linear das duas polias é a mesma.
c) A velocidade angular das duas polias é a mesma.
d) A relação entre as velocidades angulares é diretamente pro­
porcional à relação entre os raios das mesmas.
e) Nenhuma das respostas anteriores.
Resolução: Admitamos que não haja escorregamento e que a correia seja
incxtcnsível, a correia que une as polias tem velocidade escalar cons­
tante c igual à velocidade dos pontos periféricos das polias.
Assim, V,. = V P =Vi*
A B O
Para um ponto PA da periferia da polia A temos V,.A—(oA
rA
.

178. 180
Para um ponto PB da periferia da polia B vem V|*It = o)»rB.
Como V,.A= VpB, então wA
rA= wBrB-
Sendo co — 2;tf, vem:
27rfA
rA— 27tf«rB fA
rA— fB
rB
Portanto, quanto menor o raio da polia, maior sua freqücncia (número
de voltas na unidade de tempo).
Resposta: alternativa b.
7. UNIVERSIDADE DO PARANÁ — Um ventilador gira à razão de
900 rpm. Ao ser desligado, seu movimento passa a ser uniforme­
mente retardado até parar, após 75 voltas. O tempo transcorrido
desde o momento em que é desligado até sua parada completa
vale:
a) 1 s.
b) 10 s.
C) 100 S.
d) 1 000 s.
e) 0.1 s.
Resolução: Como f — 900 rpm, teremos f —900
900
60
rot
s
= 15 s-1= 15 Hz
rot
min
Portanto:
W
o = 2tzÍ W
o = 2r. . 15 W
o= 30^ rad/s
Após ser desligado, o ventilador descreve 75 voltas.
Assim, A
<
1
>— rad A
<E — 150z rad
Ao parar, w — 0 rad/s.
Lembrando que o movimento é uniformemente variado, podemos es­
crever a equação de Torricelli, na forma angular:
w2 = w24- 2aA<l> a =
0)- 0)7.
2A
<
I>
O
-' _ (30t
c
)- _ 900rv=
2 . 15077 ~~ 300tí
Sendo to = w» + at, teremos:
w — w0 0 — 3(>
t
c
“ ã —
3x:
Resposta: alternativa b.
a = —3ti rad/s2
t

179. 1. ENGENHARIA DE UBERLÂNDIA Um ponto material, animado de
um movimento circular uniforme, descreve um ângulo de 45° em 2/3 de
minuto. Nessas condições, a velocidade angular desse ponto é de:
a) rad . s“ 1.
4
b) 160^ rad . s-1.
c) —— rad . s“ 1.
160
d) lOnrad . $->.
c) — rad . s-1.
10
2. ENGENHARIA DE UBERLÂNDIA O ponteiro dos segundos de um
relógio executa um movimento circular uniforme. Pontos diferentes do
referido ponteiro terão em comum:
a) a aceleração.
b) a velocidade angular.
c) a velocidade escalar.
d) a energia cinética.
c) o produto da aceleração pelo raio.
3. FUNDAÇÃO CARLOS CHAGAS Em relação ao movimento circular
uniforme, é correto afirmar que:
a) o vetor-velocidade é constante.
b) o vetor-aceleração é constante.
c) a aceleração é centrífuga.
d) a velocidade escalar varia linearmente com o tempo,
c) a velocidade escalar angular é constante.
4. UNESP — Uma polia efetua 10 revoluções em r. segundos. Julgar as afir­
mativas:
(1) 0 ângulo de rotação da polia é de 20 rad.
(2) A freqüência de revolução da polia é necessariamente invariável.
(3) A velocidade angular média da polia c de 20 rud/s.

180. 182
5. MEDICINA DE ITAJUBÁ — Um satélite gravita em torno dc um planeta
de 6,0 . I0:<km de raio, descrevendo uma órbita circular estável a 1,0 . 105
km de altura. Se o seu período c de 2.0 anos, qual será o valor da acelera­
ção comunicada ao satélite pelo planeta?
a) Nulo.
b) (1/28) . IO-» km/ano2.
c) 9,8 . 10a km/ano2.
d) 69 . 10* km/ano2.
e) Faltam dados para resolver o problema.
6. UNIVERSIDADE DE BRASÍLIA A rotação das palhetas de um liqui­
dificador é mantida constante. O gráfico que descreve a velocidade escalar
V dos pontos das palhetas em função dc suas distâncias r ao eixo de ro­
tação é:
7. FUNDAÇÃO CARLOS CHAGAS Um satélite está em órbita circular
em torno da Terra. Desta situação, afirma-se que:
I) o vetor-velocidade c constante.
II) o período é constante.
III) o vetor-aceleração é constante.
Destas afirmações, está (estão) correta(s):
a) apenas II.
b) apenas III.
c) apenas I c II.
d) apenas I c III.
e) I, II c III.

181. 183
N
. FUNDAÇÃO CARI.OS CHAGAS — Que grandeza física, no SI, tem
como unidade dc medida s -:? (s c abreviação de segundo.)
a) Tempo.
b ) Aceleração.
c) Velocidade.
d) Comprimento,
c) Freqiicncia.
MEDICINA DA SANTA CASA — Qual dos gráficos abaixo melhor repre­
senta a velocidade angular de um movimento circular em função da fre-
qüência?
10. PUC (CAMPINAS) — Um ponto material executa um movimento circular,
percorrendo arcos iguais cm tempos consecutivos e iguais, por pequenos
que sejam. O movimento é:
a) uniforme c periódico.
b) uniformemente variado.
c) periódico mas não uniforme.
d) Nenhum dos citados (variado e uniforme),
c) Nenhuma das respostas anteriores.
11. PUC (CAMPINAS) — Os pneus de um automóvel tem circunferências de
2,10 m. Se o pneu efetua 240 rpm, a velocidade do automóvel é de:
a) 2,10 m/s.
b) 8,40 m/s.
c) 26,0 m/s.
d) 16,8 m/s.
e) 2-,6 m/s.
12. INATEL Calcular a velocidade angular, em radianos/segundo, dc um
eixo de motor de automóvel que gira a 3 600 rpm.
13. FEI-MAUÁ — Um sarilho mecanizado está girando a 60 rpm. Qual é a
velocidade de descida dc um corpo que está preso à extremidade de uma
corda ligada a esse sarilho? (O diâmetro do sarilho é de 0.3 m.)

182. 184
14. MEDICINA DE SANTOS — No instante em que um relógio bate 12 horas,
seus três ponteiros estão sobrepostos. Calcular quanto tempo após esse ins­
tante pela primeira vez um dos ponteiros forma ângulos iguais com os
outros dois.
a) 59,18 s.
b) 60.59 s.
c) 61,89 s.
d) 58,08 s.
c) Nenhuma das respostas anteriores.
15. MEDICINA DE TAUBAT6 — Duas polias de raios diferentes estão co­
nectadas por uma correia. Quando em movimento, serão iguais:
a) as velocidades angulares das duas polias.
b) as velocidades angular e linear de cada polia.
c) os períodos das duas polias.
d) as velocidades lineares dos pontos mais externos de cada polia (que to­
cam na correia).
e) as velocidades vetoriais dc todos os pontos da correia. '
16. FEI — Duas rodas tangenciam-se num certo ponto. Colocando uma delas
a girar, esta transmite movimento à segunda. Admite-se não haver escor­
regamento no ponto dc tangência. Os raios das rodas são R, - r e R, 3r.
Dar a relação entre as velocidades angulares oj1 e ü
>
2.
17. CESGRANRIO — Para um satélite em órbita circular cm torno da Terra,
qual (ou quais) das seguintes afirmações é (são) verdadcira(s)?
—
>
I) A intensidade dc sua velocidade V é constante.
II) A sua velocidade V é constante.
III) O período de seu movimento orbital é constante.
Assinale:
a) Somente I.
b) Somente I e II.
c) Somente 1 e III.
d) Somente III.
e) I, II e III.
18. CESCEA — A velocidade angular de uma roda diminui uniformemente de
40 rad/s a 20 rad/s em 5 s. Pode-se dizer que a aceleração angular neste
intervalo de tempo é:
a) nula.
b) -0,25 rad/s2.
c) —
4 rad/s2.
d) 14 rad/s2.
e) uniformerr.ente variada.

183. 19. ENGENHARIA DE L.ORENA — A velocidade angular de um motor que
gira a 900 rpm decresce uniformemente até 300 rpm, efetuando 50 revolu­
ções. Qual a aceleração angular do motor?
a) 2t. rad/s2.
b) 4t. rad/s2.
c) 2 rad/s2.
d) 3 rad/s2.
e) Nenhuma das respostas anteriores.
20. AGRONOMIA LUIZ MENEGHEL — O gráfico abaixo mostra a variação
da velocidade angular de um móvel em função do tempo. O deslocamento
angular do móvel, no intervalo de 0 s a 20 s, é de:
a) 400 rad.
b) 625 rad.
c) 1C00 rad.
d) 800 rad.
e) 600 rad.
21. FAAP — A equação horária sob a forma angular do movimento circular de
uma partícula é 4> = t2 • 6. com ângulo <
I> em radianos e o tempo em
segundos. Sabendo-se que a intensidade da aceleração total da partícula é
10m/s2, no instante t = 1s. determinar o raio da trajetória circular.
22. ENGENHARIA MAUÁ A roda da frente de um triciclo tem raio
R_ = 0,20 m e as duas rodas traseiras têm raios R2 = 0,40 m cada. O tri­
ciclo está se movimentando num plano horizontal, sem derrapar, em mo­
vimento uniformemente acelerado, com aceleração a = 2,5 m/s2. No ins­
tante da observação, sua velocidade é V = 18km/h. Determine a veloci­
dade e a aceleração angulares de cada roda, em relação ao seu respectivo
eixo.

184. 186
23. UNIVERSIDADE DO RIO GRANDE DO NORTE — Dois discos giram,
sem deslizamento entre si. como se mostra na figura abaixo. A velocidade
escalar do ponto X é 2,0 cm/s.
X
Qual é a velocidade escalar do ponto Y, em cm/s?
a) 1,0 d) 4,0
b) 2,0 e) 5,0
c) 3,0
4. (1) E. (2) E, (3) C.
5. d 6. a 7. a 8. e 9. a 10. a 11. b
12. o) — 1207: rad/s
13. V = 0.94 m/s
14. a 15. d
0)2
17. c 18. c 19. b (em móculo) 20. o
21. A trajetória circular tem raio igual a V5m .
o), = 25 rad/s
a ‘ = 12.5 rad/s2
<02 = 12.5 rad/s
a2*= 6.25 rad/s2
22.
roda dianteira
roda traseira
23. b

185. ŒUIO
7
LancamenbVerticale
Queda LivrenoVücuo

186. 188
Condições iniciais
O lançamento de um corpo é sempre influenciado pela presença
da Terra e do ar. pois a Terra atrai os corpos para sua superfície,
enquanto que o ar geralmente dificulta esse movimento.
Faremos o estudo do lançamento vertical e da queda livre nas
proximidades da superfície da Terra, admit ndo desprezíveis os efeitos
do ar. ou seja. estudaremos o corpo no vácuo e sempre num mesmo
local.

187. Aceleração da gravidade
Um corpo abandonado no vácuo, próximo à superfície da Terra,
ou arremessado com um certo impulso inicial de modo que não
atinja grandes altitudes está sujeito a uma aceleração vertical, para
baixo, de intensidade aproximadamente igual a 9,8 m/s2, devido à ação
da Terra (às vezes, para facilidades de cálculo, o valor 9,8 m/s2 é
arredondado para 10 m/s2).
1
Tal aceleração é simbolizada por g e é denominada aceleração
da gravidade local. te^v=o
1
tv
,r
!
#
.Sr i i i . t . - .
C Iri J L
corpo corpo • *
subindo
*
descendo tí
m juíV MÍMa
MOVIMENTO UNIFORMEM ENTE VARIADO
subida. MUR: descida MUA
Nas condições iniciais acima mencionadas, teremos:
Se a trajetória do corpo no vácuo for retilínea, seu movi­
mento correspondente será uniformemente variado, com
->
>ai = |g .
Referenciais
Dois referenciais podem ser usados no estudo do movimento de
um corpo no vácuo:
• referencial orientado para cima:
a = —g — —9,8 m/s2
• referencial'orientado para baixo:

188. 190 i
Equações
Para o movimento vertical de um corpo no vácuo, as equações
correspondentes serão as do movimento uniformemente variado.
• Lançamento vertical para cima — Orientando o referencial para
cima. teremos a = —g.
j V Instante qualquer (t)
v €
f Instante
''o I inicial
~A c t = o)
j
Referencial -f tr* v
s
__
iK-M
Assim:
S S.j -f- V<it — — gt*
2
V - V, - gt
V2- V2 - 2gAS
Na solução de p-oblemas.
geralmente adota-se para g o va­
lor I0m /s*, bem como S» = 0.
quando o ponto de lançamento
for admitido como origem.
Portanto, as equações do
lançamento vertical serão:
S - V„t--- — gt2
2
v — Vo •- gt
V2~ Ví - 2gS

189. • Queda livre — "Queda livre"
é uma simplificação da expres­
são “queda livre das influências
de outros fatores que não seja
a atração da Terra".
Adotado o referencial orien­
tado para baixo, teremos a — —g.
Para S,>= 0, vem:
S — Vmí + — yl"
2
V ~ Vo - gt
V» ■
- Vo I 2gS
Quando o corpo é abando­
nado a partir do repouso, tere­
mos:
V — gt
V- ^ 2gS
Casos particulares (para lançamento a partir do solo)
• Tempo de subida — No lan­
çamento vertical para cima, um
corpo levará um tempo t» para
atingir o ponto mais alto da tra­
jetória. Nesse instante, sua ve­
locidade se anula.
Assim, podemos concluir
•v»r
Importante: No ponto mais alto da trajetória o corpo terá velocidade
nulu mos sua aceleração não se anulará nesse instante. Portanto,
o corpo não estará em repouso, e sim parado instantaneamente.
Ou seja:
Ponto mais alto V — 0
da trajetória a — —g = —9.8 m/s2

190. • Altura máxima — Um corpo
lançado verticalmente para cima
atingirá sua altura máxima quan­
do a velocidade se anular.
Ou seja:
S - H„,ix <=> V ~ 0
Sendo V2= V,2
, — 2gS,
então 0 = M- — 2gHta** =>
2g
• Tempo total — Um corpo é
lançado verticalmente para cima,
a partir de um ponto adotado
como origem.
Quando retornar ao ponto de
partida, temos:
t = tr <=> S - U
Sendo S = V<>t-----— gt1,
2
vem: 0 = V..tT------— gú =>
2
(v o ---- l - 0 t T) = o = >
1) tr — 0 (instante do lançamento)
1 2V„
' 2
2 9
Vo
Como t* = ----- - podemos calcular 0 tempo de descida do corpo:
9
t, -f- td — tr —^ta — tT — t, —>
2Vo V„ V«
=>td = ------------------- ----------=>
g g g
Conclusão: O tempo de subida gasto por um corpo em lança­
mento vertical é igual ao tempo de descida correspondente ao mesmo
movimento, livre das influências do ar.

191. • Velocidade de chegada —
Quando o corpo retornar ao pon­
to de partida, teremos a veloci­
dade de chegada do movimento.
Assim: V —Vc
. <=> S — 0
Sendo V2= V* — 2gS. então:
v í = ví —2g . o=> v; = Vn=>
(movimento desenvolvido contra
o sentido do referencial)
if jf ji Conclusão: O móvel retorna ao ponto de partida com uma velo-
cldnde cuja intensidade é igual à da velocidade de lançamento.
Resumindo:
(móvel lançado do solo e retornando ao ponto de lançamento)
Altura máxima
Volocidade de , V = Vc
chegada h = 0
Tempo do
aubida
X = U
V = 0

192. Tempo total 11 = tr
de movimento 1S — 0
Tempo de Vo
descida g
Gráficos horários
Os gráficos horários refe­
rentes a um lançamento vertical
para cima. no vácuo, podem ser
mais facilmente obtidos através
de um exemplo.
Suponhamos que um corpo
é lançado verticalmente para
cima. no vácuo, com velocidade
inicial Vo = 20 m/s. num local
onde g — 10 m/s2, a partir de
uma origem no solo.
Assim, orientando o referen­
cial para cima, temos:
S = 20t-----— . 10t" =>
2
S - 20t - 5t-
Também podemos escrever
V - 20 - 10t ■
Obteremos, então, os gráfi­
cos S X t, V X t e a X t, ao
lado ilustrados.

193. Observe que:
Hinix
Vo 20*
2g 2 .
f —
Vo 20 —^
g 10
tr —
2V0 2 20
9 10
• Vc = -V o = - 2 0 = >
400
20
H ,õx — 20 m
tu —
—2 s
4 s
V e = 20 m/s
Movimentos combinados
Seja um corpo (1) lançado verticalmente para cima a partir da
origem do referencial. Nesse mesmo instante, outro corpjo (2) é
abandonado do repouso, indo chocar-se com (1) após um tempo t*.
------------- * j (2)
_________ 0 1 2 )
* Jb d )
s, s,.
Podemos, então, escrever:
1
móvel (1):t Si — V0lt gt::
móvel (2): S* = So..--------gt*
2
No encontro, teremos Si = S^.
1
Logo: V„,te
Vo,te = S
gt; — s
»2

194. Um balão que possui a velocidade ascendente de 10 m/s, ao
passar pela altura de 50 m. larga um corpo de 8,0 kg. De acordo
com esse enunciado, resolver as três questões a seguir:
1. MEDICINA DE SAN~0 AMARO — O tempo gasto para o corpo
atingir o solo foi de:
a) 4.3 s.
b) 1.0 s.
c) 3.3 s.
dj 8.6 s.
c) Nenhuma das respostas anteriores.
Resolução: Inicialmente, deve­
mos admitir que o movimento
do corpo estará livre das in­
fluências do ar.
Observe que a massa do corpo
não terá nenhuma participação
na solução do problema, pois,
no vácuo, todos os corpos sub­
metidos apenas à atração da
Terra se movimentam com a
mesma aceleração.
Enquanto o corpo estiver preso
ao balão, terá movimento reti­
líneo uniforme.
No instante em que cie se des­
prender do balão, passará a
descrever um lançamento ver­
tical para cima, com as seguin­
tes características:
• S„ = 50 m
• V„ = 10 m/s (velocidade
que tinha por estar preso ao
balão)
• g = 10 m/s2 (admitido)

195. &197
Assim, orientado o referencial para cima com origem no solo, podemos
escrever:
S = So -f V0t ------— gt2= 50 + 10t------— . 10t- =>
2 2
= > S = 50-h 101 — 5t2'
Ouundo o corpo retornar ao solo, S —0.
Logo: 5t8 — 10t —50 = 0 = > t* — 2t — 10 = 0 =>
2 ±6,6 í 1)11^4,3 51
2 II) t a —2,3 s (nâo convem fisicamente)
t
Conclusão: O corpo retorna ao solo aproximadamente 4,3 s após aban­
donar o balão.
Resposta: alternativa a.
2. MEDICINA DE SANTO AMARO — A distância percorrida pelo
corpo foi de:
a) 60,0 m.
b) 92,5 m.
c) 54.5 m.
d) 36.9 m.
e) Nenhuma das respostas anteriores.
_ áÊk. v = o .
Resolução: Lembrando que
H„
V
?,
temos:
2g
Hui«* —
I02
2 . 10
= 5
Hnl«* = 5 m
De acordo com a figura, podemos
escrever d — |Hm
i*| -f- ASa', onde
lASdl = So + Hm
ixl = 50 + 5 =
55 m.
Então: d = 5 -f- 55 = >
Resposta: alternativa a.
cl = 60 m
AS
3. MEDICINA DE SANTO AMARO — A velocidade do corpo ao cheqar
ao solo é de:
a) 43 m/s.
b) 10 m/s.
c) 33 m/s.
d) 86 m/s.
e) Nenhuma das respostas anteriores.

196. 198
Resolução: Ao chegar ao solo, o corpo terá S = 0.
Assim: V2= Vo — 2g(S - S0) = > V‘ = 102 - 2 . 10 . (0 - 50) = >
= > Vc
2= 100 4- 1 000 = > v;’rrr 1 100 =>
O sinal menos (—) indica que o movimento c desenvolvido contra a
orientação do referencial adotado.
Admitindo que o enunciado se refira à intensidade da velocidade de
chegada, teremos Vc s* 33 m/s.
Resposta: alternativa c.
V, - -3 3 m/s
4. UNIVERSIDADE DO PARANÁ — Sabendo que um projétil foi im­
pelido verticalmente de baixo para cima com velocidade de
250 m/s. qual a altura atingida pelo projétil?
a) 25 m
bO 250 m
cj 3 125 m
d) 8 375 m
e) 9 375 m
5.
Resolução: Lembrando que para o
sistema de referência indicado na
figura H„
Võ
2g
-, então:
H
(250)* _ 62 500 _ Hnit
2 . 10 20
=> Hm
á* — 3 125 m
v
Resposta: alternativa c ____ (r
~
So
V = 0
Referencial
PUC (SÃO PAULO) — Um projétil é atirado verticalmente de baixo
para cima com velocidade Vo — 25 m /s. Uma pessoa situada a
30 m de altura vê o projétil passar na subida e. após um intervalo
do tempo At, o vê voltar. Desprezando a resistência do ar c su­
pondo a aceleração local da gravidade 10 m/s'2, o tempo At decor­
rido entre as duas observações foi de:
a) 0.5 s.
b) 1.0 s.
c) 2.0 s.
d) 2,5 s.
e) 3,0 s.

197. - * í
r r 199
Resolução: Orientando o referencial verticalmente para cima a partir
do ponto de lançamento, teremos:
S,j r 0 m
V
<, — 25 m/s
a = —g — —10 m/s2
S = 30 m
Assim: S —Sn V0t -f —
2
at2
1
10t2
5t2- 25t -j- 30 = 0 t2 —5í
I
1
30 = 0 + 25t - —
m— K"
Its = 3 s
Portanto, o móvel passará pelo
observador durante a subida
(instante 2 s) c durante a des­
cida (instante 3 s). gastando
para isso um intervalo de tem­
po At = 3 — 2 = I s.
Logo: ! At — 1 s
Resposta: alternativa b.
6. MEDICINA DE SANTO AMARO — Um nadador pula verticalmente
de um trampolim de 10 rn de altura. Ao atingir a água, sua velo­
cidade é dc. aproximadamente:
a) 20 km/h.
b) 50 km/h.
c) 58 km/h.
d) 60 km/h.
e) 72 km/h.
Resolução: Orientando o refe­
rencial para baixo, a partir do
trampolim, poderemos escrever:
•= 0 So = 0 m
S = 10 m
a = -f-g = +10 m/s2
V|, r 0 m/s
Portanto:
V2= V,; + 2a(S - So) = *
V2= 0 + 2 . 10 . (1 0 - 0 )
= > V2= 200 =>
_
_ = > V = 10 Í2 m/s = >
=> V sí 14 m/s

198. 200
Como 1
m km
3,6--------- , decorre:
V 5- 50 km /h
m
V = 14-----= 14 . 3,6 =
s
Resposta: alternativa b.
7. MEDICINA DE POUSO ALEGRE — Um corpo em queda livre, par­
tindo co repouso, percorre certa distância d vertical após 2 se­
gundos de queda. Logo, a distância percorrida em 6 segundos,
contados desde o início da queda, será igual a:
a) 9d.
b) Gd.
c) 12d.
d) 2d.
e) 3d.
Resolução: Orientando o referencial verlicalmentc para baixo, pode­
mos escrever:
S = So -f V0t -r — gt2==>
2
=>S —So= V0t-f- — gt2==>
2
= > AS = V,,t + ~ gt2
Como o corpo é abandonado,
Vo = 0.
1
— gl*-
I AS
Portanto: AS —
Para t = 2 s, AS = d.
Logo, d = — g . 22
2
Referencial
AS
g = ---- (D
2
I
Para t = 6 s, AS’^ ---- g . 6a = > AS’= ---- g . 36 =
=>AS’ = 18g (2)
Substituindo (1) em (2), vem:
AS’= 18 [ AS’ = 9d
Resposta: alternativa a.

199. 'i& n d â m 201
8. PUC (SÃO PAULO) — De um helicóptero que desce verticalmente
é abandonada uma pedra quando o mesmo se encontra a 100m
do solo. Sabendo que a pedra leva 4 s para atingir o solo e su­
pondo g = 10m/s2, a velocidade de descida do helicóptero, no
momento em que a pedra é abandonada, tem valor igual a:
a) 25 m/s.
b) 20 m/s.
c) 15 m/s.
d) 10 m/s.
e) 5 m/s.
Resolução: Desprezando as influências do ar e adotando um referencial
vertical orientado para baixo com origem no ponto em que a pedra
foi abandonada, podemos escrever:
S = 100 m
S0— 0 m
Vo= VM
a = 4-g = 4-IO m/s*
t = 4 s
Logo, sendo S = S0 -j- V0t •
1
2
9
'I
+ at2= > 100 = 0 4-
Vm . 4 + ---- . 10.4*
1
20
1liei
Vw — 5 m/s
Resposta: alternativa c.
9. ENGENHARIA DE SÃO JOSÉ DOS CAMPOS — Um corpo cai em
queda livre percorrendo a primeira metade de sua trajetória em
1 s. A trajetória inteira será percorrida em:
a) 2 s.
b) (1 + 0.5) s.
c) V 2 s .
d) 1
V"2
s.
e) Nenhuma das respostas anteriores.

200. 202
Resolução: Adotando o referencial vcrticalrncnte orientado para baixo,
ccm origem no ponto onde o corpo foi abandonado, teremos:
V0= 0 m/s, S„ = 0 m e a = -fg = -4-10 m/s2
Logo, S = — gl2.
Para a primeira metade da trajetória, teremos:
S '= — . 10 . 12=5
2
S’ = 5 m
Como S = 2S teremos S = 10 m.
Para a trajetória toda, vem:
1 2
S = — gtT
2
10 = — . 10tr
2
Origem
tv — V 2 s
Referencial
?
$
Resposta: alternativa c.
10. CESCEA — Do alto de um edifício abandona-se uma pedra no
instante exato em que, do solo, lança-se outra pcd'a. vert cal­
mente. com velocidade inicial apenas suficiente para atingir o
topo do edifício. As duas pedras devem se cruzar a uma altura,
medida a partir do solo, equivalente a:
a) 75% da altura do edifício.
b) 25% da altura do edifício.
c) 60% da altura do edifício.
d) 50% da altura do edifício.
e) Nenhuma das anteriores.

201. 203
Resolução:
• Cálculo da altura do edifício:
A pedra lançada do solo (pedra 2) terá altura máxima h equivalente
à altura do edifício.
Assim, orientando o referencial verticalmente para cima a partir
VÍ
do solo, teremos h
2g
(D-
• Função horária da pedra 1:
Podemos escrever ht = h(l -f- V0 t — -i— gt2,
i i 2
onde h0l = h e V0l = 0.
Logo, hi — h — — gt2.
2
Substituindo (1), vem hi
Võ
2g
• Função horária da pedra 2:
---- gt* (2).
2
1
Podemos escrever h2 h0 -f- V„ t — ---- gt2.
2 2 2
Observando que V0 _ V0 e h(. = 0, temos:
h2—V0t ------— gt2 (3)
2
• Kncontro das pedras:
No encontro, hi = h2.
De (2) c (3), vem
v í
2g
1
gt* = V0t
V*
2
= V0t
gf
2g
V,
2g
Substituindo em (2), temos:
• Vo 1
hi = -----------------g
2g 2
v í
4g2 2g
V.. Võ . 3
=> h, = ----
H
_V^
2g

202. 204
Lembrando que
Vo
2g
h, vem ht = h, = 75%h
Resposta: alternativa a.
1. MEDICINA DE POUSO ALEGRE O vulcão Sangay, no Equador, é o
mais turbulento da Terra. Ele é capaz de projetar lava a uma altura de
12,5 km. A velocidade com que a lava sai do vulcão deve ser da ordem de
(despreze as variações da aceleração da gravidade com a altitude):
a) 1.8 . 108km/h. d) 140 km/h.
b) 25 . 104 m/s. . c) 16 km/h.
c) 500 km/h.
2. MEDICINA DE POUSO ALEGRE" Uma bola é lançada para cima com
uma velocidade do 20 m/s (g = 10 m/s2). Indique a afirmativa errada
(despreze a resistência do ar):
a) A bola atinge uma altura de 20 m.
b) No ponto mais alto a velocidade da bolac nula.
c) No ponto mais alto a aceleração da bola é nula.
d) A bola retorna ao ponto de partida com uma velocidade de 20 m/s.
c) A bola volta ao ponto de partida depois de 4 s.
3. UNIVERSIDADE DE SANTA CATARINA — Uma bola é lançada ver-
ticalmente para cima com velocidade V„ e retorna ao ponto de partida após
T segundos.
Desprezando a resistência do ar. indique o gráfico que, mais propriamente,
representa a velocidade (V) da bola cm função do tempo (t):

203. 205
4. ENGENHARIA DE SANTOS — Lança-sc um corpo verticalmente para
cima. No instante cm que ele pára:
a) é nula a velocidade do móvel.
b) é nula a aceleração do móvel.
c) é nula a força que age no móvel.
d) é nulo o impulso no móvel.
e) Nenhuma das alternativas anteriores é correta.
5. MEDICINA DE SANTO AMARO — Um projétil é lançado verticalmente
para cima com a velocidade de 200 m/s. A velocidade vetorial média de­
pois que o projétil atinge novamente o solo é de:
a) 4.00m/s.
b) 200 m/s.
c) 100 m/s.
d) 0 m/s.
e) Nenhuma das anteriores.
6. MEDICINA DE SANTO AMARO — Em relação ao teste anterior, a dis­
tância total percorrida pelo projétil foi de:
a) 0 m.
b) 2 000 m.
c) 4 000 m.
d) 8 000 m.
c) Nenhuma das anteriores.
7. UNIVERSIDADE DE PERNAMBUCO Um morteiro lança uma gra­
nada, verticalmente, com uma velocidade inicial de 400 m/s. Desprezando-
-sc a resistência do ar e sendo a aceleração local da gravidade igual a
10 m/s-, podemos concluir que a altura máxima alcançada pela granada,
cm metros, é de:
a) 12 000. d) 4 000.
b) 10 000. e) 6 000.
c) 8 000.
8. UNIVERSIDADE DE PERNAMBUCO — Em relação ao problema ante­
rior, o tempo que a granada leva para atingir a altura máxima, cm segundos,
é de:
a) 20. d) 40.
b) 10. e) 50.
c) 30.

204. 206
9. UNIVERSIDADE DO PARÁ — Em uma experiência de laboratório veri-
ficou-sc que a velocidade de lançamento de um corpo, para que este atin­
gisse uma cena altura, era V, quando lançado verticalmente. Um aluno
repete a experiência, porém imprime ao corpo uma velocidade 2V c conclui
que, ão atingir a mesma altura do primeiro ensaio, o corpo tem velocidade:
a)
b) V.
c)
C
) V3V.
10, CESCEA — Um foguete com combustível próprio sobe vcrticalmcntc com
velocidade constante até uma altura h. quando termina o combustível; daí,
cai livremente. Qual dos gráficos representa melhor o espaço percorrido
(S) pelo foguete cm função do tempo (t>?
e) Nenhuma das respostas anteriores.
11. MAPOFEI — Um tijolo cai, de um prédio em construção, de uma altura
de 20 m. Qual a velocidade do tijolo ao atingir o solo? Quanto tempo
gasta na queda? Desprezam-se as resistências opostas pelo ar ao movimento.
(Adotar g = 10,0 m/s2.)
12. UNIVERSIDADE DE PERNAMBUCO — De uma ponte deixa-se cair
uma pedra que demora 4 s para chegar à superfície da água. Sendo a acele­
ração local da gravidade igual a 10 m/s-, pode-se concluir que a altura da
ponte, em metros, c de:
a) 40. d) 90.
b) 80. , c) 60.
c) 110.
r-

205. 207
13. MAPOFEI — Ã altitude de 20 m abandona-se uma bola de chumbo cm
repouso. Adotar g = 10 m/s2. Com que velocidade a bola atinge o solo?
14. MEDICINA DE ITAJUBÁ Um corpo em queda livre caiu de uma
altura h. Se ele partiu do repouso, qual será sua velocidade após ter per-
corrido ——h?
3
a)
fib
2 d) V
n -gh
b)
3 íh e ) vr
-gh
c) 4 - 8h
15. CKSGKANRIO — Você deixa cair, a partir do repouso, urna bilha de aço
do uma altura h,. c mede um tempo t, ate que ela atinge o solo. De que
altura ha você deve deixar cair esta bilha, também a partir do repouso, para
que o tempo de queda seja 2tt?
u) ha = 2hj
b) ha = 4hx e) h... = f l hj
16. UNIVERSIDADE DO PARA Um balão desce, verticalmente, com
velocidade constante; à altura de 100 m, um objeto desprende-se do balão
e atinge o solo após 4 s. A velocidade de descida do balão, considerando
g = 10 m/s2, é de:
a) 5 m/s. d) 10 m/s.
b) 25 m/s. c) 9 m/s.
c) 15 m/s.
17. MEDICINA DE TAUBATÉ — Um pára-quedista, quando a 120m do
tolo. deixa cair uma bomba. Esta leva 4 s para atingir o solo. Qual a velo­
cidade dc descida do pára-quedista? (g = 10 m/s2)
k) 1m/s d) 8 m/s
b) 2 m/s c) 10 m/s
c) 5 m/s*
*
M
. UNIVERSIDADE DO PARÁ — largamos um corpo de uma altura dc
l-Mm. Queremos dividir a altura de queda cm duas partes tais que sejam
pcicorridas em tempos iguais. Supondo g 10 m/s2, podemos di/cr que
»
»
»partes serão iguais a:
«) 25 m e 119 m. d) 44 m c 100 m.
b) 2Hm c 116 m. ç) 72 m c 72 m.
u) .16m c 108 m.

206. 208
19. CESGRANRIO — A laje do teto
de uma sala deixa gotejar água
da chuva, caindo as gotas com
freqüência constante.
Uma fotografia instantânea mos­
tra que as distâncias entre três
gotas consecutivas são. respectiva­
mente. 30 cm e 50 cm (ver figura).
Concluímos que. desde que a
resistência do ar seja desprezível,
a gota que caiu antes da gota (1)
se encontra, abaixo desta, a urna
distância de:
a) 50 cm.
b) 70 cm.
c) 20 cm.
20. CESCEA — Um menino solta uma bola de gude de um apartamento a
uma altura h do solo. A bola, logo após chocar-se contra o solo, retorna
com uma velocidade 20% inferior à que tinha imediatamente antes do cho­
que. A máxima altura atingida pela bola será de (desprezar a viscosidade
do ar):
1 20
a) ----- h. d) ----- h.
10 25
b) — h.
0
e) h.
c) — h.
25
CESGRANRIO — Uma pequena bola de borracha (elástica) cai vertical-
mente a partir do repouso, bate numa superfície dc aço horizontal, onde
repica, etc. Desprezando a resistência do ar. qual dos seguintes gráficos
melhor representa a velocidade da bola em função do tempo?
(3)
( 2)
30 cm
(1)'
50 cm
d) X0cm.
e) 40 cm.

207. 209
22. UNIVERSIDADE DO PARÁ Duas bolas são lançadas, simultanea­
mente, de uma mesma altura 11, com velocidades verticais Vx e Vs: uma
para cima e outra para baixo. Desprezando a resistência do ar e sendo
V, = V2 V, o atraso na chegada de uma das bolas ao solo, relativamcntc à
outra, é:
a)
b)
c)
2V
Í5
V2
8
H
V
d)
e)
2V2
g
2H
Vg
2
.%
, AMAN — Considerando-se que a velocidade do som no ar é de 320 m/s,
deixa-se cair uma pedra em um poço. ouvindo-se o som do choque contra
O fundo 4,25 s após a pedra ter sido solta. A profundidade do poço é de:
u) 35 m. d) 75 m.
b) 52 m. c) 80 m.
c) 60 m.
24. IIA — Cinco bolinhas de aço estão presas por eletroímãs ao longo de uma
reta r de equação y = kx. As bolas estão em posições cqüidistantcs. tais que
d 0.5 m. Uma bolinha () pane da origem ao longo de x (mesa horizontal
icm atrito) com V = 2 m/s, constante, no mesmo instante cm que todas as
outras são desligadas dos eletroímãs. Assinale abaixo o valor de k para que
O se choque com a bola n.° 4. (Usar g = 10 m/s-.)
•») 0.62
1») 1,25
o) 1,87

208. 210
25. PUC (SAO PAULO) De cois ponto? A eB situados sobre a mesma ver­
tical, respectivamente a 45 m e 20 m do solo. deixa-se cair, no mesmo
instante, duas esferas. Uma prancha se desloca no solo horizontalmcntc,
com movimento uniforme. Observa-se que as esferas atingem a prancha
em pontos que estão a 2 m de distância um do outro. Nessas condições,
supondo g = 10 m/s- e desprezando a resistência do ar. podemos afirmar
que a velocidade da prancha, em m/s, é de:
a) 2. d) 1.
b) 3. e) 2,5.
c) 4.
26. UNIVERSIDADE DE BRASÍLIA — Uma partícula é lançada vertical­
mente, no vácuo, com velocidade inicial V0. Como se sabe, sua velocidade
decresce continuamente di.rante a subida e cresce continuamente durante
a descida. Julgar as afirmativas, indicando se estão certas ou erradas:
a) O vetor-aceleração da partícula é o mesmo na subida e na descida.
b) Em cada ponto da trajetória o vetor-velocidade da partícula tem a mesma
intensidade na subida e na descida.
c) Na descida, ao passar no ponto onde foi lançada, a intensidade do vetor-
-velocidade da partícula é V0 e seu vetor-aceleração é igual àquele no
topo da trajetória, onde sua velocidade é nula.
d) O tempo gasto na subida é maior que o gasto na descida.
27. INATEI. — Atira-se verricalmente uma bola de forma que, ao fim de 4s,
retorna ao ponto de partida. Calcular a velocidade iniciai com que foi lan­
çada. Admitir g —10 m/s2.
28. IME — Um projétil é lançado verticalmente do solo com velocidade inicial
de 200 m/s. A uma altura II a carga do projétil explode; o ruído da ex­
plosão é recebido no solo 15 s após o lançamento. Despreze a resistência
do ar e use os valores de 10 m/s2 para a aceleração da gravidade c de
300 m/s para a velocidade do som. Calcule:
a) o intervalo de tempo entre o lançamento e a explosão.
b) a altura em que se deu a explosão.
29. FUVEST — Duas bolinhas são lançadas verticalmente para cima, a partir
dc uma mesma altura, com mesma velocidade inicial de 15 m/s mas com
intervalo dc tempo dc 0.5 s entre os lançamentos.
a) Dcsprc/ando a resistência do ar, faça, num mesmo sistema de eixos, os
gráficos da velocidade em função do tempo para as duas bolinhas. Indi­
que nos eixos as unidades dc medida.
b) Qual o instante etn que as alturas das duas bolinhas coincidem? Justi­
fique.
30. EAAP — Do topo de um edifício deixa-se cair, a partir do repouso, uma
pedra que leva 2 s para atingir o solo. Supondo que a aceleração da gravi­
dade do lugar seja 10 m/s2, pedem-se:
a) a velocidade com que a pedra atinge o solo.
b) a altura do edifício.

209. 31. MAP0FE1 — De uma ponte de altura h = 20 m, um menino deixa cair
uma pedra com a intenção de atingir uma lata flutuante. A correnteza tem
velocidade V = 3,0 m/s. A que distância da vertical pela pedra deve si­
tuar-se a lata no instante da iargada? Admitir g —10 m/s2.
32. MAPOFE1 — Um elevador desce com velocidade V0 = 2,0 m/s, quando
o cabo sc rompe. Qual a velocidade após queda livre h = 0,25 m? Admitir
g = 10m/s2.
33. ITA — Um corpo cai, em queda livre, de uma altura tal que, durante o
último segundo de queda, ele percorre 1/4 da altura total. Calcular o tempo
dc queda, supondo nula a velocidade inicial do corpo.
a)
1
----------s
2 —y7
b)
c)
t _ 2
2 + v'7
2
t =
2 - y T
s
s
d) t =
3
2 — ÍJ
4
3 —yT
1 ii 2. c 3. a 4. a 5. d 6. c 7. c 8. d 9. e 10. c
11.V 20 m/s: t = 2.0 s.
J li 13. V 20 m/s 14. e 15. b 16. a 17. e 18. c 19. b 20. c 21. a 22. a
21 n 24. d 25. o
J n •) C b) C; c) C; d) E.
27. V0 - 20 m/s
28. •) At 10 s;
bj II 1500 m.

210. 212
b) As alturas das duas bolinhas coincidem 1.75 s após o ançamento
da 1.* bolinha.
30. a) 20 m/s:
b) 20m
.
31. d - 6 m
32. V = 3 m/s
33. C
I

212. Introdução
Uma mosca voa do chão de um carro até seu teto enquanto o
veículo se desloca sobre uma estrada.
Conhecendo as características do movimento da mosca em re­
ação ao carro (MOVlll/c) e as características do movimento do carro
em relação ao solo (MOVc/J , desejamos determinar as características
do movimento da mosca em relação ao solo (MOVm
/J .
Análise do vetor-deslocamento
Observando o esquema abaixo, podemos escrever:

213. ' ï ;l= -
215
Ard/* — Ar:;i/c ■" à rt.h onde<
r Ar„,/i é o vetor-deslocamento da mos­
ca em relação ao solo.
—
>
Arinícé o vetor-deslocamento da mos­
ca em relação ao carro.
v
—
7
Arc/J é o vetor-deslocamento do car­
ro em relação ao solo.
Análise do vetor-velocidade
Para os vetores-velocidade podemos escrever:
I
Vm
/t é o vetor-velocidade da mosca
em relação ao solo.
= V»/i -r V,/w onde <
Vm
/C é o vetor-velocidade da mosca
em relação ao carro.
Ví/S é o vetor-velocidade do carro em
relação ao solo.
Análise do vetor-aceleração

214. Jll/• : V-n/c — Yc/s
"4
^ Tm/s é o vetor-aceleração da mosca em
relação ao solo.
—
>
r m
-c é o vetor-aceleração da mosca em
onde < ,• .
relaçao ao carro.
Tf/* é o vetor-aceleração do carro em
v relação ao solo.
_____________________ _________________________________________________________
Esta relação somente é válida se os corpos envolvidos descreverem
movimento de translação
Em caso de rotação, uma terceira parcela será acrescentada no segundo
membro da igualdade (aceleração de Coriolis).
T^adicionalmente, dá-se o nome de movimento relativo ao movi­
mento da mosca em re ação ao carro; de movimento de arrastamento
ao movimento do carro em relação ao solo; e de movimento absoluto
ao movimento da mosca em relação ao solo.
Ou seja:
M O V m /c — movimento relativo
M OV./»m ovim ento de arrastamento
MOVni/h movimento absoluto
Aplicações
A teoria discutida pode ser aplicada nos seguintes casos:
• Determinação dos elementos vetoriais associados ao movimento
de um passageiro que se desloca no interior de um trem.

215. /> ^ v 217
• Determinação da velocidade de um barco em relação às margens,
conhecendo a velocidade do barco em relação às águas e a das águas
em relação às margens.
/ - ■ ff?
*• u ; r i ® % % .
Jk
— 5c
Mm
VelocMade^ rftr bSfSíPéro relação ^
$ ò água;
Velocidade :ia
C - w r : '
Velocidade
do barco em
relação à margem.
*e-
.x-VelocdScfe <io barco
k1 em relação à água.
Velocidade
-----------uJaJjgua.
Velocidade do ba^ço
em relação à margem.
• Determinação da velocidade das gotas de chuva que caem verti­
calmente em relação a um observador que caminha horizontalmente.
Lr

216. 218
• Determinação da velocidade de um avião em relação ao solo,
conhecendo a velocidade do avião em relação ao ar e a do ar (vento)
em relação ao solo.
• Determinação da velocidade dos aviões que decolam de um porta-
•aviões que se move em relação ao mar.
• Determinação da velocidade da Lua em relação ao Sol. conhe­
cendo a velocidade da Lua em relação à Terra e a da Terra em relação
ao SoI.
Lua
Terra V

217. ----------
• Aná ise do movimento de uma carga transferida de um local para
outro, quando ela é elevada verticalmente ao mesmo tempo em que
ó transportada lateralmente.
Generalização
A ilustração abaixo esquematiza o raciocínio necessário para
estudar o movimento de um corpo A em relação a vários referenciais
(B. C. D e E): ^ ^
* © ^ ©
O
%
©
©
Para a velocidade, por exemplo, teríamos:
—
> —
> —
> —
> —
>
VA/D -f- Vb/c ■
+
■Vc/d -f- Vd/e = Va/e
Princípio da Simultaneidade (Galileo)
Para a solução de exercícios que envolvam a variável tempo,
devemos nos lembrar do Principio da Simultaneidade, enunciado por
Galileo Galilei:
"O movimento de um corpo pode ser imaginado como a com­
posição de outros movimentos realizados separadamente c ao mesmo
tempo".

218. 220
1. ENGENHARIA DE SÃO CARLOS — Um barco a motor, desenvol­
vendo toda a potência, sobe um rio a 20 km/h e desce a 48 krn/h.
Qual a velocidade das águas do rio?
a) 18 km/h d) 14 km/h
b) 28 km/h e) Nenhuma das anteriores.
c) 10 km/h
Resolução: Sendo / u = velocidade do barco em relação às águas,
—
> —
>
V./t = velocidade das águas cm relação à terra e Vb/t = velocidade do
barco em relação à terra, vem:
—
>
Vb/i — Vi,/# -j- Va/t.
Barco descendo o rio
yb/e Ve
"T1
b,t
Barco subindo o rio
Observando os esquemas acima, concluímos:
barco descendo o rio: Vb/rt = Vb/a + V*/t = > 48 = Vh/a -f Va/t (i)
barco subindo o rio: Vb/t = Vb/a —Va/t = > 20 := V*,/« — / t (2)
Somando (1) e (2), vem 68 = 2Vb/„= Vb/4 — 34 km/h
Substituindo em (1), temos: Va^t —48 — Vb/a = > Vu/L 48 — 34
VH
/, — 14 km/h
Resposta: alternativa d.

219. / V ^ 221
2. MEDICINA DE ITAJUBÁ — Um barco atravessa um rio. seguindo
a menor distância entre as margens, que são paralelas. Sabendo
que a largura do rio é de 2,0 km. que a travessia é feita em 15.0
min e que a velocidade da correnteza é de 6.0 km/h, pergunta-se:
Oual a intensidade da velocidade do barco em relação às águas?
a) 2,0 km/h d) 10 km/h
b) 6,0 km/h e) 14 km/h
c) 8,0 km/h
Resolução: Sendo.Vb
/, s= velocidade do barco em relação às águas,
—
* —
►
V,/t = velocidade das águas cm relação à terra c Vb/t = velocidade do
barco em relação à terra, vem: ^t*/1 — ^ h/t "f" ^ */l-
O barco vai atravessar o rio, perpendicularmente às margens, com
movimento retilíneo uniforme.
1
Sendo L = 2,0 km e t = 15,0 min —------h, vem:
4
Observando a figura, podemos escrever:
vf/H- v;/t + Vb
/t=> vb
2
/t = 62+ 82= 36 + Ó
4
Vb/4 = 100 Vt/a — 10 km/h
Note que, para atravessar o rio perpendieularmente às margens, o barco
deverá inclinar-se de modo a formar um ângulo a cm relação à sua pre­
tendida trajetória.
Podemos, então, escrever:
V./, 6 . . 3
0,75 = > a - 37a|
V '
tga =
8
tg a —
4

220. 222
Complementação:
Suponhamos que o barco lente atravessar o rio orientando-se perpen­
dicularmente às margens. Em vez de atingir a margem oposta no
ponto A, irá atingi-la no ponto B, sofrendo um desvio representado
pelo ângulo $.
Teremos, então:
V'u/i 6
tg (3—----- -— = ------= > tg 0,6 =>
Vj,/,, 10
ií s 31°
Considerando o barco como ponto material, também podemos escrever:
AB -------------------
------— tg (í = > AB = L . tg 3 = 2 . 0,6 = > AB — 1,2 km
Determinemos o tempo de travessia do barco:
L = Vb/. . t
2
10
0,2 h => t = 12 min
Conclusão: Neste segundo caso o tempo de travessia é o menor possível,
embora no primeiro caso a distância percorrida seja mínima.
Resposta: alternativa d.
3. MEDICINA DE SANTO AMARO — Um avião que viaja de uma
cidade A a uma cidade B, com a velocidade de 300 km/h em re­
lação ao ar. é atingido por um tufão de 60 km/h, que sopra a um
ângulo de 60! relativamente ao seu curso. A velocidade do avião
em relação â Terra, em km/h, 6 de:
a) 334.
b) 360.
c) 240.
d) 180.
e) Nenhuma das respostas anteriores.
'I
I

221. 223
lloioluçfio: Sendo VA
/, = velocidade do avião em relação ao ar, V„/f =
—
*
velocidade do ar cm relação à terra c VA
/t = velocidade do avião
em relação à terra, temos:
VA
/t — VA/â -f- Va/t
V v i = VAA + V~/, - 2 . VA/â . Vn/t . cos 120° =>
-> = 3002 -J- 60*’ — 2 . 300 . 60 . ^-----l
— ) =>
>VÍ/t = 90 000 4- 3 600 -f 18 000 = 111 600 =>
>V j/t = 111 600 => ! VA/t - 334 km/h
Kcspn.sta: alternativa a.
O enunciado abaixo refere-sc às questões 4 e 5.
Um carro move-se a 80 km/h sob uma tempestade. Seu moto-
rlnta observa que a chuva deixa, nas janelas laterais, marcas incli-
nndns que formam um ângulo de 80* com a vertical. Ao parar o
curro ele nota que a chuva cai verticalmente. São dados ainda:
Non 80° = 0.98 e cos 80° — 0.17.
4 Ml DICINA DA SANTA CASA — Supondo constante o valor da
volocldade de queda da chuva, pode-se afirmar que esse valor
d. em relação ao carro parado, mais aproximadamente igual a:
ii) 82 km/h. d) 14 km/h.
b) 80 km/h. e) 10 km/h.
C) 78 km/h.

222. 224
— >
Resolução: Sendo V a/t = velocidade do automóvel em relação à torra,
—
» _ —
*
Vc/a = velocidade da chuva cm relação ao automóvel e Vo/t = velo­
cidade da chuva cm relação à terra, temos:
VcA = Vc/. + V./,
Da figura, vem:
V
Vc /t
= tg80° => vc/«
V,yi ~ 14 km/h
V>/t ___«o_
tg 80° 0,98
0,17
80
5,7
a 14 =>
Ouando o carro parar, a velocidade da chuva cm relação ao carro
coincidirá com a velocidade da chuva cm relação à terra, ou seja:
V c / t — ^ c/a —
Resposta: alternativa d.
VV/n saí 14 km/h
5. MEDICINA DA SANTA CASA — O valor da velocidade da chuva,
em relação ao carro, enquanto este está se movendo, é mais
aproximadamente igual a:
a) 82 km/h. d) 14 km/h.
b) 80 km/h, e) 10 km/h.
c) 78 km/h.
Resolução: Da figura da questão 4, vem:
V.A _____ _ Va/l
c/a
sen 80°
Vc/â es 82 km/h
c/a
sen 80°
Vc/a =
80
0,98
Resposta: alternativa a.

223. 6. MAPOFEI — Uma roda de raio R — 0,25 m rola sem escorregar
sobre um plano horizontal. Um ponto P do seu eixo geométrico
tem velocidade constante V, com intensidade igual a 4,5 m/s. O
ponto A da periferia é fixo em relaçáo à roda e, no instante t = 0 s,
coincide com o ponto O, origem do sistema de eixos cartesianos
—
>
ortogonais xOy, com Ox horizontal e paralelo a V e Oy vertical.
aj Calcule a velocidade angular do ponto A em relação ao ponto P.
b) Calcule a intensidade da velocidade de A cm relaçáo ao sistema
~ 3T
xOy, no instante t = -----. sendo T o tempo necessário oara
4
que a roda efetue uma volta completa.
Resolução: Os pontos da roda
simultâneos:
• Rotação: os pontos da roda
terão movimento circular
uniforme em relação ao seu
eixo central.
Assim, os pontas da perife­
ria terão velocidade Vr cm
relação ao centro P (veloci­
dade relativa).•
• Translação: o eixo central
tem velocidade Vt em rela­
ção ao solo (veloeidade de
arrastamento). Assim, todos
os pontos da roda estarão
dotados dc velocidade de
translação V,.
estarão dotados de dois movimentos

224. 226
Conclusão: Os pontos da periferia da roda terão velocidade absoluta
(cm relação ao solo) igual à soma vetorial das velocidades dc trans­
lação e rotação, ou seja:
V,b» = Vt + VP
Como a roda não escorrega, seu ponto de contato com o solo possui
Vab
% nula.
Assim, necessariamente, Vt = Vr.
Designaremos V, e Vr por V, simplificadamcnte.
O ponto de contato com o solo é denominado centro instantâneo dc
rotação.
a) Sendo V = 4,5 m/s, cm relação ao centro geométrico P, teremos:
V 4,5
to = ------==> to = ----------=>
R 0,25
o
>— 18 rad/s
b) Quando t = -----, a roda
4
3
efetua------de volta.
4
Assim, o ponto A sc loca­
lizará na extremidade di­
reita do diâmetro horizontal.
Em relação ao solo, teremos:
Va = V2-1- V2 = 2V2= > VA= V /T = 4,5
VA= 4,5 m/s
Resposta: to = 18 rad/s e V A = 4,5 y T m / s .

225. *
I
I. MEDICINA DE VASSOURAS — Um barco tem uma velocidade de
22,32 km/h rio abaixo e de 13,68 km/h rio acima. Podemos dizer que a
velocidade do rio é de:
«) 5,00 m/s. d) 1,20 m/s.
b) 7,20 m/s. e) 4,00 m/s.
c) 4,32 m/s.
i. PUC (CAMPINAS)— Um piloto deseja voar para Leste, de A até B. c.
cm seguida, voar para Oeste, retornando a A. A velocidade do avião, no
#(, é V' c a velocidade do ar em relação ao solo c U. A distância entre
A c B é L c a velocidade do avião no ar, V', é constante. Suponha que
ii velocidade do vento esteja dirigida para l.este (ou para Oeste); nestas
condições, o tempo de viagem de ida e volta será:
u) t =
2LV'
V' - U
b) t =
LU
V' - u
c) t =
2LV'
V'2 - U2
d) t =
2L
V'
c) Nenhum dos valores acima.
3. FATEC — Uma ferrovia estende-se paralclamente a uma rodovia. Um
automóvel, a 108 km/h, ultrapassa um trem de 180 m que corre a 72 km/h.
(1) Sc os sentidos forem concordantes, a ultrapassagem demora I8s.
(2) Sc os sentidos forem opostos, a ultrapassagem demora 3,6 s.
(3) Sc o trem estivesse parado c o automóvel passasse a 36 km/h, a ultra­
passagem demoraria J8 s.
u) Somente (1) é correta,
b) Somente (1) e (2) são corretas,
e) Todas as afirmativas são corretas.
d) Nenhuma das afirmativas é correta.
e) Alternativa diferente das anteriores.

226. 228
4. MEDICINA DE POUSO ALEGRE — Uni canociro, usando um barco que
desenvolve uma velocidade de 20 m/s (cm relação à margem), atravessa um
rio de lOOm dc largura, dirigindo-sc perpendicularmente às margens.
O tempo gasto na travessia é de:
a) 2.85 s.
b) 4,0 s.
c) 5,0 s. j
d) 6.67 s.
c) Não é possível calcular sem se conhecer a velocidade da correnteza.
5. FATEC — Em relação ao ar, um avião voa para Leste com velocidade de
120km/h, e está sujeito ao vento sul com velocidade de 50km/h. Julgar
as afirmativas:
(1) 0 avião voa aproximadamente para ENE (és-nordeste).
(2) A velocidade resultante do avião é de 130 km/h.
(3) Se o avião voasse para o Norte, sua velocidade seria dc 170 km/h.
6. ENGENHARIA DE SÂO JOSÊ DOS CAMPOS Um cidadão caminha
com velocidade de 1m/s sob a chuva. Para não sc molhar, ele mantém
seu guarda-chuva inclinado de modo a formar um ângulo <
|> em relação à
vertical. A tangente de <
t>é igual a 0,25. Neste caso, a velocidade da chuva
que cai vcrticalmente c de:
a) 4 m/s. d) 0,10 m/s.
h) 5 m/s. e) Nenhuma das respostas anteriores,
c) 0.25 m/s.
7. MACKENZIE — Um motorista, dirigindo a 100 ^ k m /h sob uma tem­
pestade, observa que a chuva deixa, nas janelas laterais, marcas inclinadas
que formam um ângulo de 60° com a vertical. Ao parar o carro, ele nota
que a chuva cai vcrticalmente. Podemos afirmar que a velocidade da chuva
relativa ao carro, quando ele estava em movimento, era de:
a) 200 km/h. d) 180 V^km/h.
b) 100 y'Tkm/h. e) Nenhuma das anteriores.
c) 200yTkm/h.
Dois corpos sc encontram a uma certa distância quando começam a deslo-
car-sc sobre uma mesma reta, aproximando-se um do outro. Os gráficos
da velocidade do corpo I c do deslocamento do corpo II em função do
tempo são mostrados abaixo:
1 2 3 4 5 tfs)

227. Supondo que o corpo I sc encontre na origem dos espaços no instante
t 0 s, responda às questões de números 8 e 9.
H
. ClíSCEA - Qual a distância inicial entre ambos?
«) 70 m d) 120 m
b) 80 m e) 130 m
c) 100 m
V
. CliSCEA — Qua! a velocidade do corpo I em relação ao corpo II no
primeiro segundo?
u) —10 m/s
b) —
20 m/s
c) 30 m/s
10. AMAN — Dois carros partem
oo mesmo tempo do ponto A
mostrado na figura. O primeiro
vai em direção ao ponto B com
velocidade constante de 40km/h
e o segundo vai em direção ao
ponto C com velocidade constan­
te de 30 km/h. Qual a velocidade
escalar do primeiro cm relação
ao segundo?
a) 80 km/h
b) 70 km/h
c) 60 km/h
d) 50 km/h
c) 40 km/h
d) 40 m/s
c) 70 m/s
II I UVEST — Um cilindro de madeira de 4,0 cm de diâmetro rola sem desli­
zai entre duas tábuas horizontais móveis A e B. como mostra a figura.
I m determinado instante, a tábua A se movimenta para a direita, com
velocidade de 40cm/s. e o centro do cilindro se move para a esquerda, com
veloeidude de lOcm/s. Qual é, nesse instante, a velocidade da tábua B em
Intensidade e sentido?

228. 230
12. FEI — Uma roda de raio
R = 20 cm rola sem escorregar,
paralelamente a um plano verti­
cal fixo. O centro C da roda tem
velocidade constante Vr = 5 m/s.
c —
Qual a intensidade da velocidade
do ponto B no instante em que
o diâmetro AB é paralelo ao pla­
no de rolamento?
13. ENGENHARIA MAUÁ — Um automóvel trafega com velocidade cons­
tante V = 72km/h. As suas rodas tèm diâmetro I) = 0,50 m e rodam sem
escorregar. Determine:
a) a velocidade angular dc rotação da roda em relação ao seu eixo.
b) a velocidade instantânea, em relação ao solo, do ponto da roda que c
simétrico daquele que faz contato com o solo.
14. FEI — Um automóvel, cujas rodas possuem um diâmetro d = 0.5 m, move-
-sc com velocidade constante, percorrendo a distância d = 56,5 km no inter­
valo de tempo At = 30 min. Determinar:
a) sua velocidade, em m/s.
b) o número de rotações por minuto de cada roda.
Adotar r. = 3,14.
1. d 2. c 3. c 4. c
5. [1) E (O avião tem a direção sul-lcste.)
(2) C
(3) E (O avião teria velocidade de 70 km/h em relação ao solo.}
6. a 7. a 8. c
9. e (Cuidado com V „ = —40 m/s.)
10. d
11. V —60cm/s para a esquerda.
12. V„ - 5 V Tm /s
13. a) «o = 80 rad/s;
b) V = 144 km/h.
14. a) V = 31.4 m/s:
b) f = 1,2 . 103 rpm.

229. C
fflT
U
LO
9
Gstudo de u
mM
ovim
ento
atravésde suasírojeções

230. 232
Apresentação do problema
Suponha que estejamos interessados em estudar o movimento
de uma bola chutada por um goleiro ao bater o tiro de meta.
£
A análise desse movimento não é fácil, pois sua trajetória não
é circular e sua velocidade tem intensidade variável, não apresen­
tando nenhuma das características dos movimentos estudados ante­
riormente (movimento uniforme ou movimento uniformemente va­
riado).
Pcrém, se projetarmos o movimento segundo duas direções con­
venientes e estudarmos o comportamento dessas projeções, podere­
mos obter dados suficientes para reconstituir o movimento da bola.

231. w e m d & u 233
Projeções do vetor-posição
Geralmcnte, a decomposição do movimento é feita segundo dois
eixos ortogonais x e y.
Assim, se um ponto mate­
rial P descreve um movimento
qualquer seguindo a trajetória L
num dado instante t, vamos es-
tudar seu vetor-posição r.
Projetando o ponto P nos
eixos x e y, teremos:
r = rx + ry
—
» —
»
Os vetores rs e rx são deno­
minados componentes vetoriais
de r (grandeza vetorial).
—
► —
»
Ou seja: rx — componente horizontal de r:
—
+ —
>
ry — componente vertical de r.
As intensidades desses vetores-componentes, associadas a sinais
Indicativos de suas orientações em relação aos eixos x e y , são deno­
minadas projeções do vetor r (grandezas escalares).
Assim, para a figura em questão:
r(I) = projeção horizontal de r;
—
>
r(r) = -fry - projeção vertical de r.
r, — componente do vetor-posição r segundo a direção x (grandeza vetorial);
r, — intensidade do vetor-componente r,.;
r(») — projeção do vetor-posição r no eixo x (grandeza escalar);
r y — componente do vetor-posição r secundo a direção y (grandeza vetorial);
—
►
T, — Intensidade do vetor-componente rt ;
tr — projeção do vetor-posição r no eixo y (grandeza escalar).

232. 234
Podemos então escrever:
r~— r'fx. -4 rf„
r xi — rcos a
ri,) = rscn a
Projeções do vetor-velocidade
No instante t. o ponto material P está sujeito a uma velocidade V.
Os vetores-componentes V, e V* indicam os vetores-velocidade
referentes ãs projeções do movimento.
Assim:
Para as projeções dos vetores V* e V ,, na figura em questão, te­
remos:
V,x) = +V* projeção horizontal de V*:
—
>
V ,v)= —Vy - projeção vertical de Vv.

233. (% frva a % 2 -----------------------------------------------------------------------------
V, — componente do vetor-velocidade V segundo a direção x (grandeza
vetorial);
Vx — intensidade do vetor-componente V,;
V(x) — projeção do vetor-velocidade V no eixo x (grandeza escalar):
Vy — componente do vetor-velocidade V segundo o direção y (grandeza
vetorial);
V, — intensidade do vetor-componente Vy ;
V(y>— projeção do vetcr-veiocidade V no eixo y (grandeza escalar).
Podemos então escrever
v —v;xl i v:,>
V(x) — Vcos |5
V „, - Vsen 3
Projeções do vetor-aceleração
—
>
No instante t. o ponto material P está sujeito a uma aceleração y.
—
> —
>
Os vetores-componentes yx e Yy indicam os veto-es-ace eração
referentes às projeções do movimento.
Assim: r ~ r * • r.v onde-
Yx : componente horizontal de y.
—
> —
>
Yy : componente vertical de y.
A y
Y
,

234. 236
Para as projeções dos vetores yx e yy. na figura em questão, te­
remos:
Yu) = -f Y x - projeção horizontal de yx;
Y(y, = -f Yy - projeção vertical de yy.
Yx — componente do vetor-aceleração y segundo a direção x (grandeza
vetorial):
y x — intensidade do vetor-componente y x;
Y j0 — projeção do vetor-aceleração no eixo x (grandeza escalar):
y^ — componente do vetor-aceleração y segundo a direção y (grandoza
vetorial):
v y — intensidade do vetor-componente y v;
—
♦
— j . . . . . ------1. — s_ n0 (JjX0 y (grandeza escalar).
Funções horárias das projeções
Como os movimentos descritos pelas projeções do ponto ma­
terial P são retilíneos, os módulos das grandezas vetoriais referentes
aos movimentos serão iguais aos módulos das grandezas escalares
correspondentes.
Podemos, então, montar as funções horárias relativas aos movi­
mentos das projeções: S = f(t). V = f(t) e a = f(t).
diminando a variável t nas funções horárias S = f(t) das proje­
ções. podemos obter a equação da trajetória do ponto material P.
Exemplo:
Sejam y = 3 + 6t — ôt2 (1) e x = 2t (2) as funções horárias das
projeções do movimento de um ponto material P.
r = rm f Y?,)
Podemos então escrever: y lx. — ycoso
v . . . v = : v < 3 p n ^
Yiy> — Tsen

235. 237
Podemos, então, escrever x — 2t => t = — .
2
Substituindo na expressão (1). vem:
y = 3 - 6 ( y ) - 8 - ( t V =
3x 2x2= >
y = —2x2-f 3x + 3
Assim, a trajetória do ponto material será uma parábola de equa-
Importante: Não confundir equação da trajetória (y X x) com função
horária do movimento (S X t).
1. MAPOFEI — Um ponto material realiza um movimento plano tal
que suas coordenadas cartesianas são dadas pelas equações:
x = 1 + 3t
y = 1 -f- 4t
com x e y em metros e t em segundos. Determinar:
a) a velocidade do ponto material.
b) a equação da trajetória.
c) a equação horária do movimento, tomando como origem do
espaços o ponto P(1, 1).

236. 238
Resolução: A projeção horizontal do ponto material realiza um movi­
mento retilíneo uniforme de função horária x = I + 3t, onde x„ = 1m
e Vx — 3 m/s, constante.
A projeção vertical do ponto material realiza um movimento retilíneo
uniforme dc função horária y = 1 -f 4t, onde y0= 1 m e Vy = 4 m/s,
constante.
a) Podemos, então, escrever:
V2 - V2 -f Vf- :=> V2 — 3a + 4- = 9 + 16
Da figura, vem: tga = — —= —
Vx 3
Portanto, o ponto material estará sujeito a uma velocidade de in­
tensidade constante igual a 5 m/s, com direção indicada pelo ângulo
, 4
a cuja Rangente vale ------.
3
Seu sentido está indicado na figura.

237. 239
h) Das funções horárias das projeções, vem:
x = 1 -f 3t=>t =
y = 1 -f 4t = > t =
X —1 x — 1 y —1
1
1
3 ‘ 4
> => 3y — 3 = 4x — 4 =>
=>
4 1
4 3 3
A trajetória do móvel será uma reta de declive — e que corta
o eixo v no valor — — m.
3
c) Ao iniciar a contagem dos tempos (t = 0 s), o móvel sc encontra
na posição:
í x = 1m (x= 1+ 3
t = H - 3 . 0 = 1)
y = 1 m (y = 1 -f- 4
t = l 4 .0 = 1
)
Se adotarmos este ponto como origem do referencial, teremos Srt — 0.
Logo, sendo o movimento do móvel descrito com velocidade cons­
tante 5 m/s, teremos:
S = S0- V t= > S = 0 + 5t=> S - 5t (SI)
Ou seja, o móvel descreverá um movimento retilíneo uniforme de
função horária S — 5t no SI.
O movimento de um ponto material é descrito pelas equações
x — 8t — 4t2 e y = 6t — 3t2 (SI).
Esta explicação refere-sc às questões de 2 a 4.
2. MEDICINA DE SANTOS — A trajetória do ponto pode ser expressa
pela equação:
3
b) y = — x.
4
C) y = 4 — 3x.
3
d) y = — x.
2
e) Nenhuma das respostas anteriores.
Resolução: Para a projeção horizontal do movimento do ponto ma
terial, temos:
X = 8 t — 4 t2 = > x = 4 (2 t — t-) = > 2 t — t- = — (1)
4

238. 240
I
Para a projeção vertical do movimento do ponto material, temos:
y = 6t — 3t2= > y = 3(2t - t2) = > 2t - t2 = -y- (2)
Comparando (I) e (2), vem:
Portanto, a trajetória do ponto material será uma reta que passa pela
3
origem, de declive — .
Resposta: alternativa b.
3. MEDICINA DE SANTOS — A velocidade V do ponto pode ser ex­
pressa pela equação:
a) V = 4-t-2t.
b) V = 10(1 - t).
c) V - 1 - t.
4
e) Nenhuma das respostas anteriores.
Resolução: O movimento da projeção horizontal do móvel é unifor-
memente variado.
Assim, sendo x = 8t —4t2, temos V0(í) = 8 m/s e a(X
) = —8 m/s2.
Logo, para Vm = V0(i) -f- a<
K
>
t, vem V(x) = 8 — 8t (1).
O movimento da projeção vertical do móvel é uniformemente variado.
Assim, sendo y = 6t — 3t2. temos V0|y| = 6 m/s c a(yl = —6 m/s2.
Logo, para V(yl = Vfl r) -f a(y)t, vem V(y, ~ 6 — 6t (2).

239. Lembrando que Va = V?x, + V*,,, subsliuiindo (1) c (2) temos:
Va = (8 - 8t)2 + (6 - 6t)2= 82(1 - t)2 + 62(l - t)2 = >
= > V2= 64(1 - t)2 + 36(1 - t)2= 100(1 - t)2=>
= > V = 10 — 10t (função velocidade de MUV)
V = 10(1 - t )
Conclusão: () movimento do ponto material é retilíneo e uniformemente
variado, sendo progressivo entre os instantes 0 s c I s e retrógrado a
partir de t = 1 s.
Resposta: alternativa b.
4. MEDICINA DE SANTOS — A aceleração do ponto é de:
a) 4 m/s2.
b) 3 m/s'-.
c) (3/4) m/s2.
d) 10 m/s*.
e) Nenhuma das respostas anteriores.
Resolução: Lembrando que a<x»= Y
<
*>— —8 m/s2 e =. y(>
., —
= —6 m/s2, teremos:
r 2= r?*> + r7r> = 64 36 = 100=» Y= 10 m/s2

240. 242
Portanto, o vctor-aceleração do movimento terá intensidade 10m/s2,
direção indicada pelo ângulo a tal que tg a = — , e sentido indicado
4
na figura.
Resposta: alternativa d.
5. UNIVERSIDADE DE JUIZ DE FORA — As equações do movimento
de uma partícula são x = 3cos t e y = 3sen t.
Seu movimento é:
a) retilíneo uniforme.
b) retilíneo uniformemente variado.
c) retilíneo uniformemente retardado.
d) circular.
e) Nenhum dos movimentos mencionados.
Resolução:
Sendo x = 3cos t, vem x2 = (3cos t)- = > x2= 9cos2t (1).
Sendo y = 3sen t. vem y2 = (3scn t)2= > y2= 9sen2t (2).
Somando (1) e (2) membro a membro, teremos:
x2 + y* = 9cos2 1 -f 9sen2 1 = > x2 + y* = 9(sen2 1 -f cosa t)
v ___ j
Esta última expressão representa uma circunferência de raio 3 e centro
na origem do referencial.
Resposta: alternativa d.

241. wsT&nd/im & 243
I. UNIVERSIDADE DE MOGI DAS CRUZES — Em relação a um refe­
rencial cartesiano xOy, uma partícula se move segundo as equações
x = 8t —4t- c y = I2t - 6t2
A equação cartesiana da trajetória será:
a) y = 3x d) y = —3 -f- 5x.
2 e) y = —
2x.
b) y = 14 - 10x.
c) y = 2 + 2x.
•) 3y j . t.
H) y/T. t.
o) •! yTJ . (1 - t).
d) 4t.
c) y r • t.

242. 244
4. CESCEA — O movimento de um corpo é descrito pelas equações abaixo,
onde x determina sua posição na direção leste-oeste e y determina sua posi­
ção na direção norte-sul:
x = —3+10t c y = - 4 + 2t + 2t2
Sendo x c y dados em metros e t em segundos, a velocidade escalar do corpo
no instante t = 2 s é:
a) 10 V?m/s. d) 9,4 m/s.
b) 2y/lB m/s. e) Nenhuma das anteriores.
c) 20 m/s.
5. CESCEA — Na figura abaixo, a linha pontilhada indica um arco de cir­
cunferência de raio OP = 1m, sobre o qual uma bola de tênis P é cons­
trangida a se mover com velocidade angular de intensidade constante
ü) = —
— rad/s. Em cada choque com a parece e o solo. o movimento da
2
bola inverte de sentido, provocando um movimento de vaivém. Conside­
rando que no instante inicial a bola P está em contato com o solo, qual
dos gráficos seguintes indica o melhor deslocamento Q (projeção de P sobre »
o eixo x - solo) em função do tempo?

243. A figura mostra dois gráficos, um representando a coordenada x e o outro
a coordenada y, cm função do tempo, de duas esferas I e 2, de mesma massa,
em movimento sobre uma superfície plana. As que>tões de 6 a 8 referem-se a
este enunciado.
6. CESCEA — Durante qual dos intervalos de tempo a velocidade das duas
esferas foi nula?
ft) (1 s, 2 s)
b) (2 s, 3 s)
c) (3 s, 4 s)
d) (4 s, 5 s)
7. CESCEA Durante qual dos intervalos de tempo o movimento da esfera
I foi paralelo ao eixo Ox com velocidade não-nula?
a) (1 s, 2 s)
b) (2 s, 3 s)
c) (3 s, 4 s)
d) (4 s, 5 s)
H
. CESCEA — Em que instante as duas esferas sc chocaram?
u) 1 s
b) 1,5 s
c) 2 s
d) 3s

244. 246
A figura a seguir representa um móvel M em movimento circular uniforme,
com velocidade escalar V e raio r. As duas próximas questões referem-se a
esse enunciado.
9. CESCEA — Se V(*>
segundo os eixos Ox c Oy da figura, e se o sentido do movimento for anti-
-horário, então:
a) Vlx) é máxima c Vlv, mínima em C.
b) V,x) é máxima e V<
y
) mínima em O.
c) V(X
I c máxima em 1) e V,yl mínima em C.
d) y (%
) é máxima çm l> e Vly) mínima em B.
e) Nenhuma das respostas anteriores.
10. CESCEA A intensidade da aceleração centrípeta é:
a) máxima cm A.
b) constante c diferente de zero.
c) constante c igual a zero.
d) mínima cm A.
e) Nenhuma das respostas anteriores.
11* FEI — O movimento de um ponto material é descrito pelas equações
x —(t + 1)-' e y = (t + l)"2, onde I representa tempo. Determinar a equa­
ção da trajetória descrita pelo ponto material.
1. a 2. d
3. c (0 módulo da aceleração é a
4. a (A trajetória do corpo é uma
5. b G. c 7. d 8. b 9. c 10. b
11. y = -
1

245. C
A
P
IT
U
L
O
10
Lançamento
Oblíquo noVdcuo

246. Introdução
Ouando um canhão dispara um projétil não-verticalmente, num
local onde a influência do ar é desprezível, se não houvesse a ação
da gravidade seu movimento seria retilíneo e uniforme segundo a
—
>
direção do vetor-velocidade V0.
No entanto, devido à atração exercida pela Terra, o projétil vai
caindo à medida que se translada, dc forma que. decorridos diversos
intervalos de tempo, ao invés de se encontrar nas posições A, B. C,
D o projétil encontrar-se-á, respectivamente, nas posições A B C D’.
Conclusão: O lançamento de um projétil, não-verticalmente, nas
proximidades da Terra, livre das influências do ar. é a combinação
de um movimento retilíneo uniforme com uma queda livre.

247. 249
Lembrando que na queda livre, a partir do repouso, os desloca­
mentos escalares são obtidos através da expressão AS = —
— gt
2
conforme vimos anteriormente, poderemos analisar a combinação de
movimentos referentes ao lançamento de um projétil não-vertical-
mente.
Na figura abaixo, no primeiro segundo de movimento, enquanto
o projétil se desloca de uma distância d. sofre, simultaneamente,
uma queda igual a AS. onde. para g = 10rn/s2. teremos:
t
Analogamente, poderemos calcular os diversos valores de AS
paru os Instantes t = 2 s. t = 3 s, t = 4 s, etc., construindo a tabela
abaixo.
Instante
t(s)
Deslocamento
retilíneo
Queda vertical
(AS)
0 0 0
1 d 5 m
2 2d 20 m
3 3d 45 m
4 4d 80 m
O movimento resultante é curvilíneo e sua análise é bastante
complexa. Para estudar esse movimento é necessário decompô-lo
em dois eixos ortogonais.

248. 250
Elementos de um lançamento oblíquo
No lançamento oblíquo de um corpo no vácuo são elementos
essenciais:
• V0 — velocidade inicial de lançamento.
• a — ângulo de lançamento.
• g*— aceleração local da gravidade.
Análise das projeções
Vamos decompor o lançamento oblíquo de um móvel segundo as
direções horizontal e vertical e estudar o movimento de suas projeções.
—
r
Inicialmente, analisemos a aceleração y do movimento.
A única aceleração a que está submetido o corpo é a da gravi­
dade. __________
Ou seja: “ 9

249. 1
251
• Componente r*: como g é vertical, não haverá componente hori-
—
r
zontal da aceleração Y-
Ou seja: Tx = 0
Logo. a aceleração escalar au>
também será nula. isto é. a(x)= 0 .
Conclusão: A projeção horizontal do móvel descreve um movi­
mento retilíneo uniforme.
— ► — >
• Componente Yy: como g é vertical, o vetor-componente-vertical da
aceleração coincide com a aceleração da gravidade g .
Ou seja: Tt = g
Assim, a aceleração escalar a(y) será constante e igual a —g. isto
6, a(y, = —g, constante.
, r Conclusão: A projeção vertical do móvel descreve um movimento
'"^retilíneo uniformemente variado.
Equações das projeções
• Projeção horizontal — MRU: x = Xo + V x
>
t
Sendo V,*) = V0(x) e Vo(xl = V0cos a, vem:
x = xo -f- Vocos a . t

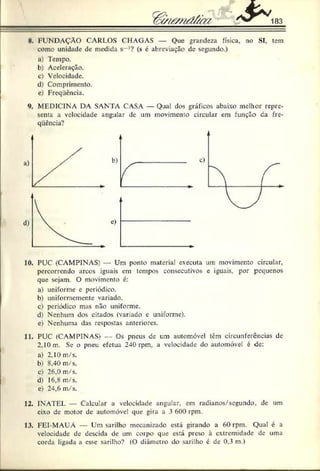
250. 252
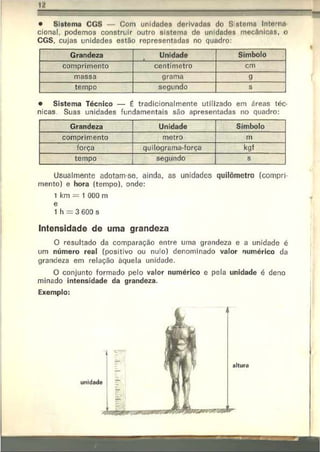
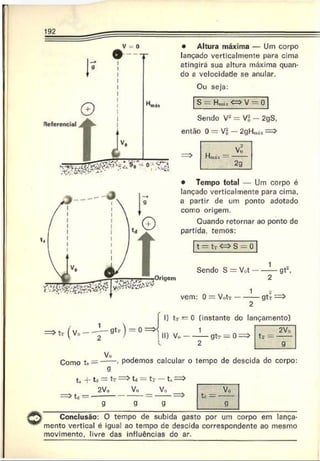
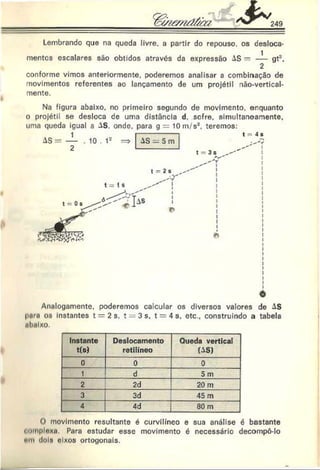
Projeção vertical — MRUV:
y = y. + V o ,„ t+ — a r)t2
Sendo Vu<
v) = V(,sen x e a(Jr) = —g. vem:
------------ ]-------
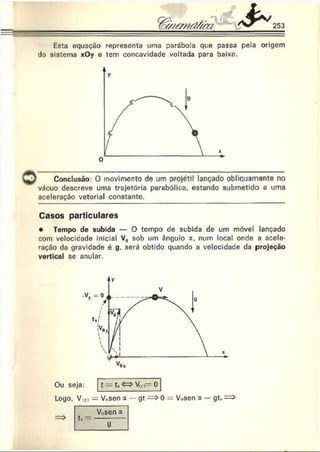
y — yi> : Vosen a . t -----— gt~
V(yi = Vo(y, + 3(y)t Viy., — Vc.sen f — gt
V(yi —Vnly, -f* 2a.»(y — yo) V‘„ - VÔsen* a —2g(y — y0)
Simplificações
Para x0 = 0. vem:
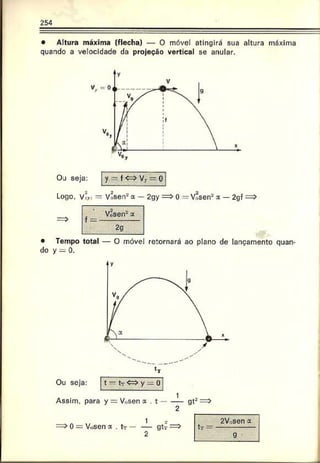
Para y0 — 0, vem:
x — Vocos a . t (1)
1
y — Vosen a . t --------gt-
2
V(y) = Vosen a — gt
VÍyl — Vosen2cf. — 2gy
(2]
Equação da trajetória
Da equação (1), vem t =
Vocos a
Substituindo^em (2). obteremos a equação da trajetória do móvel
= - (-------------- ) + (tg x) .
' 2V“cos*x '

251. Esta equação representa uma parábola que passa pela origem
tio sistema xOy e tem concavidade voltada para baixo.
Conclusão: O movimento de um projétil lançado obliquamente no
vácuo descreve uma trajetória parabólica, estando submetido a uma
aceleração vetorial constante.
Casos particulares
• Tempo de subida — O tempo de subida de um móvel lançado
com velocidade inicial Vu sob um ângulo a. num local onde a acele­
ração da gravidade é g. será obtido quando a velocidade da projeção
vertical se anular.
Ou seja: t t, <=>Vjr - 0
Logo, V,r>= Vosen a — gt => 0 = V.,sen a — gt.
Vosen a
g

252. 254
• Altura máxima (flecha) — 0 móvel atingirá sua altura máxima
quando a velocidade da projeção vertical se anular.
O j seja: y — f< ^ V 7— o
Logo. víy, = Võsen8a — 2gy => 0 = Vosen2a — 2gf
• Tempo total — O móvel retornará ao plano de lançamento quan­
do y = 0.
Ou seja: t — tT <=>y — 0
Assim, para y = V„sen a . t ---- gt2
2
0 = Vosen x . tT — — gtr
2
tr —
2V isen a

253. ^ 255
• Alcance horizontal — O alcance horizontal do móvel ocorrerá
quando ele retornar ao plano horizontal de lançamento.
Ou seja:
Sendo x —
x — D <=>t — t r
Vocos a . t, vem:
D = Vecos a
2V.,sen x
D
VÜ
. 2sen x . cos x
sen 2a
Observando a expressão do alcance, notamos que o mesmo valor
do D será obtido para dois ângulos de ançamento complementares,
desde que a velocidade inicial V0 seja a mesma.
Daj = Da.
y <=>X: - a> — 90'

254. 256
A intensidade da veloc:dade de chegada do móvel ao plano hori­
zontal de lançamento é igual à intensidade da velocidade de lança­
mento.
Análise da aceleração
—
> —
>
A aceleração vetorial do lançamento oblíquo é constante (y = g).
Decompondo-a nas direções tangencial e normal à curva, obtemos as
— > — >
acelerações componentes a , e ac , respectivamente, em cada ponto.
Importante: Como a intensidade da aceleração tangencial é variável,
também a intensidade da aceleração escalar é variável. Logo. o lan­
çamento oblíquo não é um movimento uniformemente variado.

255. Lançamento horizontal no vácuo
Una esfera move-se oom movimento retilíneo uniforme sobre
uma mesa.
Se caso não houvesse a atração da Terra, ao perder contato com
a mesa. o corpo continuaria a se mover em trajetória retilínea, com
a mesma velocidade. Mas como há essa atração, o corpo cairá verti­
calmente. ao mesmo tempo em que se deslocará horizontalmente
com movimento uniforme.
Lembrando que AS — — gt2, para g = 10 m/s2. teremos AS — 5ta.
Podemos, então, preencher a tabela seguinte.
Instante
t(s)
Deslocamento
horizontal
Queda
vertical (AS)
0 0 0
1 d 5 m
2 2d 20 m
3 3d 45 m
4 4d 80 m

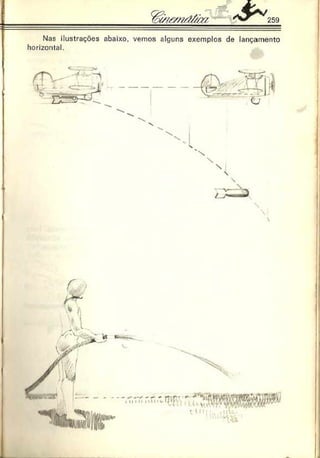
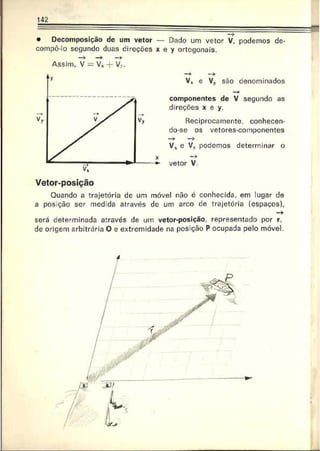
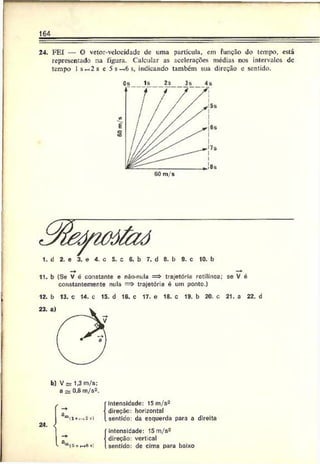
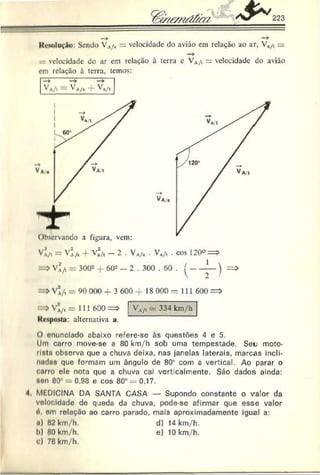
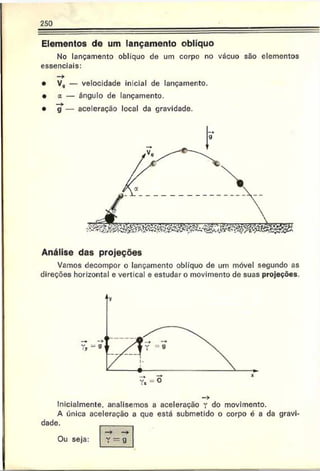
256. 258
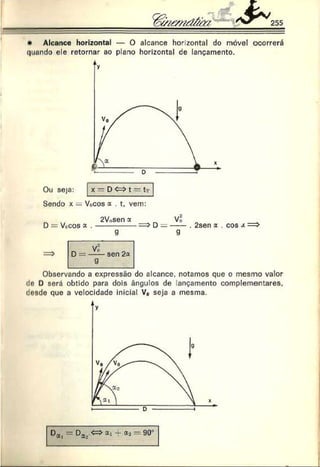
Esquematicamente, teremos a figura a seguir, onde a trajetória
do móvel é um arco de parábola. Considera-se desprezível a in­
fluência do ar.
M
o lançamento horizonte), o vetor-coinponente horizontal da velocidade é
sempre constante. O vetor-componente-vertical da velocidade tem
intensidade crescendo linearmente com o tornpo a partir co repouso.
Para a projeção horizontal do movimento, vem X -n Votl (1).
Note que. no instante do lançamento horizontal, o vetor-compo-
nente-vertical da velocidade é nulo.
Ou seja: V.»v= 0 ==>Vn( . - 0.
Logo, para a projeção vertical do movimento, vem:
gt2 (2]
De (1), vem t — -----.
Vo
Substituindo em (2). vem
x'-'

258. 260
Considerações finais
Pe o fato de essa teoria ser aplicada no lançamento de artefatos
bélicos, o lançamento oblíquo de um projétil também recebe o nome
de lançamento balístico.
Observe que, num lançamento horizontal e nuna queda livre
simultâneos, os movimentos verticais são idênticos. Assim, os corpos
estarão sempre na mesma horizontal durante todo o movimento.
W' ■
I
l I
I
I I

259. I

260. 1. UNIVERSIDADE DE SANTA CATARINA — Um projétil com massa
m c lançado com uma velocidade V0, formando um angulo a com
a horizontal, conforme mostra a figura.
Desprezando a resistência do ar. pode-se afirmar que a sua velo­
cidade no ponto mais alto da trajetória é:
a) Vosen a.
b) nula.
c) Vi.cos a -f gt.
d) V.sen a —gt.
e) VnCOS a.
Resolução: No ponto mais alto da trajetória parabólica a projeção ver­
tical tem velocidade nula. Assim, a velocidade do projétil coincidirá com
a velocidade da sua projeção horizontal.
Como a projeção horizontal do lançamento balístico é um movimento
retilíneo uniforme, seu vetor-velocidade será sempre constante e igual
—
>
ao vetor-componente-horizontal da velocidade dc lançamento V0.

261. &
263
2. PUC (RIO DE JANEIRO) A curva C da figura abaixo representa
a trajetória de um projétil disparado por um canhão na superfície
da Terra. ConsideranOo desprezível a resistência do ar, indique
—
►
qual das opções melhor representa o vetor-velocidade V e o vetor-
-aceleração a do projétil, quando o mesmo está no ponto A de sua
trajetória.
Resolução: Livre da resistência do ar, o lançamento balístico está do­
tado de aceleração constante e igual à aceleração da gravidade (inten­
sidade g = 9,8m /s2, direção vertical e sentido de cima para baixo).
y

262. 264
Lembrando que a velocidade de um móvel é sempre tangente à tra­
jetória, no ponto A teremos os vetores velocidade e aceleração ilus­
trados.
Resposta: alternativa c.
3. FUNDAÇÃO CARLOS CHAGAS — Uma pedra é jogada livremente
para cima numa direção que forma um ângulo de 302 com a hori­
zontal no cairpo gravitacional terrestre, considerado uniforme.
Ignorando o atrito com o ar, no ponto mais alto alcançado pela
pedra a intensidade de:
a) sua aceleração é zero.
b) sua velocidade é zero.
c) sua aceleração atinge um mínimo, mas não c zero.
d) sua velocidade atinge um mínimo, mas não é zero.
e) seu vetor-posiçãc, em relação ao ponto de lançamento, é má­
xima.
Resolução: No vértice da trajetória parabólica dc um lançamento balís­
tico, a velocidade tem intensidade mínima mas não-nula, conforme
vimos no exercício 2
A aceleração correspondente será vertical e igual à aceleração da gra­
vidade. Embora seja constante e não-nula, a aceleração do movimento
balístico não caracteriza um movimento uniformemente variado, pois
sua aceleração componente tangencial, cuja intensidade c igual à da
aceleração escalar, não é constante.
No vértice da parábola a aceleração tangencial é mínima e de inten­
sidade igual a zero, enquanto que a aceleração centrípeta tem inten­
sidade máxima e é igual à aceleração da gravidade.
Resposta: alternativa d.

263. 265
4. MEDICINA DE SANTO AMARO — Um projétil é lançado obliqua­
mente para cima. com a velocidade de 100 m./s, numa direção que
forma um ângu o de 60° com a horizontal. Após 4.0 s, a intensidade
da velocidade vetorial do projétil é:
a) 50 m/s.
b) 87 m/s.
c) 47 m/s.
d) 69 m/s.
e) Nenhuma das respostas anteriores.
»
Resolução: Vamos decompor o movimento balístico segundo suas pro­
jeções:
• projeção horizontal: V,x) —V„
Vw>= V0cos <
I>= 100 . cos 60°
• projeção vertical: V m = Vrt)v) _ gt
v ir> = V0sen <
I>— gt
V,„ = 100 . sen 60« - 9,8 . 4 = joq
V„) 46,8 m/s
Portanto, V = Vx-f- V,..
Donde: V = VXJ, +V", a
V =
=
=68,9 m/s
VTíoF + (46,8)2 s* V 4 700 .
Resposta: alternativa d.

264. 266
5. MEDICINA DA SANTA CASA — Um canhão, em solo plano e hori­
zontal, dispara uma bala com ângulo de tiro de 30u
. A velocidade
inicial da bala é de 500 m/s. Sendo de 10 m/s2 o valor da acele­
ração da gravidade no local, a máxima altura da bala em relação
ao solo será, em km, um valor mais próximo de:
a) 3,1. d) 6,3.
b) 3.5. e) 7,5.
c) 4,5.
Resolução: Lembrando que a flecha do lançamento balístico é dada
V0 sen2a
por I = iw* —---------------, logo:
2g
f _ (500)2 . sen230° 250 000
2 . 10 ~ 80
Portanto, |f s= 3,1 km 1.
3 100 m = 3,1 km
Resposta: alternativa a.
6. MEDICINA DE SANTO AMARO — Um corpo é iançado obliqua­
mente para cima, formando um ângulo de 30° com a horizontal.
Sabendo que o tempo de permanência no ar é igual a 6.0 s. con­
clui-se que a intensidade da velocidade de lançamento c:
a) 10 m/s.
b) 40 m/s.
c) 60 m/s.
d) 80 m/s.
e) Nenhuma das respostas anteriores.

265. Resolução: Lembrando que o tempo de duração de um movimento
balístico, descrito por um corpo que parte c chega ao mesmo plano
, . „ , . . . 2V„ sen a
horizontal, e dado por tT= --------------- , entao:
g
2V„ sen 30°
10
V , = 60 m/s
Resposta: alternativa c.
7. MEDICINA DE SANTO AMARO — Um corpo é lançado obliqua­
mente para cima com velocidade de 100 m/s. O alcance é máximo
quando:
a) a massa do corpo é igual a 10 kg.
b) o ângulo de lançamento é 0®
.
c) o ângulo de lançamento é 45°.
d) o ângulo de lançamento é 70°.
e) o ângulo de lançamento é 90°.
Resolução: Sendo o alcance horizontal de um lançamento balístico no
x , a „ V0 sen 2a ,
vacuo dado por D --------------- , D sera maxano quando sen 2a for
g
máximo, o que ocorre para 2a — 90° ou a = 45°.
Acima ou abaixo desse ângulo teremós lançamentos com alcances infe­
riores ao alcance correspondente ao ângulo de 45°.
Resposta: alternativa c.

266. 268
8. FUNDAÇÃO CARLOS CHAGAS — A figura seguinte mostra as
trajetórias de cinco projéteis (a, b, c. d. e) lançados no vácuo,
numa região onde a aceleração da gravidade é constante. Todas
as trajetórias estão num mesmo plano vertical e foram percor­
ridas em tempos iguais pelos projéteis (a subiu e desceu). Qual
deles foi lançado com maior velocidade escalar?
a) a
b) b
c) c
Resolução: O tempo de duração dc um lançamento balístico é dado
2V0sen a ,, tTg
por tT—--------------- . . V„ sen a = ------- .
g 2
Assim, para o mesmo tempo de duração, quanto maior V0, menor
sen a. Para ângulos inferiores a 90°, quanto menor o sen a, menor
o valor do ângulo a.
Conclusão: A velocidade de lançamento será maior quanto menor for
o ângulo de inclinação.
Portanto, o móvel c terá maior velocidade dc lançamento, já que seu
ângulo dc inclinação é o menor de todos os apresentados.
Resposta: alternativa e.
9. ENGENHARIA DE LORENA — Um canhão dispara um projétil sobre
o mar. horizontalmente, com uma velocidade inicial de 400 m/s,
de um ponto situado a uma altura de 100 m acima do nível do
mar. Quanto tempo o projétil gastará para atingir a água? (Dado:
g = 9,8 m/s2.)
a) 4.5 s.
b) 3 s.
c) 3.5 s.
d) 2 s.
e) 2,5 s.

267. C
è^i£m á&u 269
Resolução: No lançamento horizontal, a projeção vertical terá velo­
cidade inicial nula. O eixo de referência vertical será orientado para
baixo, a partir do ponto do disparo.
Desse modo, as equações referentes a ela serão:
(para y0 = 0) j
Para o exercício
V„» = gt
y = i - g t *
V?„ = 2gy
em questão, temos:
y = 100 m e g = 9,8 m/s2
100= — . 9,8 t2 t s- v'T0,4
2
t 4,5 s
Assim, a projeção vertical ao movimento balístico levará aproximada­
mente 4,5 s para chegar ao nível do mar. Paralelamente, este também
será o tempo que a própria bala levará para atingir a água.
Então, você perguntará: “E a velocidade horizontal de lançamento?
Não tem influencia no tempo de queda?” A resposta é não. A velo­
cidade horizontal de lançamento vai influenciar o alcance horizontal
da bala. Quanto maior a velocidade horizontal de lançamento, maior
o alcance pelo projétil; porém, o tempo de queda será sempre o mesmo,
dependendo somente da altura de lançamento para o mesmo g.
Resposta: alternativa a.

268. 270
10. UNIVERSIDADE DE VIÇOSA — Uma pessoa atira com uma cara­
bina na horizontal, de uma certa altura. Outra pessoa atira, tam­
bém na horizontal e da mesma altura, com uma espingarda de
ar comprimido. Desprezando a resistércia do ar. pode-se afirmar
que:
a) a bala mais pesada atinge o solo em um tempo menor.
b) nada se pode dizer a respeito do tempo de queda, porque não
se sabe qual das armas é mais possante.
c) o tempo de queda das balas é o mesmo, independendo de suas
d) a bala da carabina atinge o solo em um tempo menor que a
bala da espingarda.
e) a bala da espingarda atinge o solo em um tempo menor que
a bala da carabina.
Resolução: Livres da resistência do ar, sendo lançadas na horizontal
e da mesma altura, independentemente de suas massas, as duas balas
chegarão simultaneamente ao solo, embora a bala disparada pela arma
mais possante tenha um alcance maior.
Resposta: alternativa c.
11. UNIVERSIDADE DE MINAS GERAIS — Uma bolinha de gude rola
sobre uma mesa com velocidade de 40cm/s. Após sair da mesa.
cai. atingindo o chão a uma distância de 12 cm dos pés da mesa.
Pode-se concluir que a altura dessa mesa é, aproximadamente,
igual a:
a) 80 cm. d) 30 cm.
b) 45 cm. e) 100 cm.
c) 120 cm.
Resolução: A projeção horizontal do lançamento da bolinha descreve
um movimento uniforme de função horária x V0t (para x„ —0), onde
V0 é a velocidade inicial de lançamento horizontal (a projeção hori­
zontal da velocidade V0 coincide com a própria velocidade horizontal
de lançamento).
Portanto, sendo x = 12 cm c V(, =r 40 cm/ s, vem:
massas
12
x = Vw
t 12 = 40t t = 0,3 s
40
Para a projeção vertical, podemos escrever
y gl2 y 10 . (0.3)2 = 5 . 0,09 = 0.45 m ou
2 2
y = 45 cm

269. 271
Portanto, a bolinha cai dc uma altura igual a 45 cm (altura da mesa).
Resposta: alternativa b.
12. MEDICINA DE SANTOS — Um corpo é larçado horizontal e per­
pendicularmente contra o centro dc um alvo contido num plano
vertical No instante cm que o corpo é lançado, o alvo é aban­
donado e cai, conservando sua posição vertical.
O corpo atinge o alvo:
a) no centro.
b) abaixo do centro.
c) acima do centro.
d) acima e à direita do centro.
e) acima e ã esquerda do centro.
Resolução: No instante cm que
o corpo c lançado horizontal­
mente, o alvo inicia sua queda
livre. Nesse mesmo instante, a
projeção vertical do lançamento
também inicia seu movimento
de queda livre.
Como o tempo dc queda só
depende da altura e da acele­
ração da gravidade, os dois
movimentos serão descritos
paralclamcntc.
Enquanto isso, a projeção hori­
zontal do corpo lerá movimento
dirigido para a trajetória ver­
tical descrita pelo alvo.

270. 272
Como tudo isto ocorre simultaneamente, em dado instante, quando a
projeção horizontal atingir a vertical descrita pelo alvo, haverá o en­
contro do corpo com o alvo.
Assim, sempre haverá choque entre os dois. Todavia, se o alvo não
se desprender e cair, o corpo passará por baixo dele, pois sua trajetória
é parabólica.
Resposta: alternativa a.
13. ESCOLA TÉCNICA DO PAPANÁ — Um bombeiro tenta apagar o
incêndio do 4.° pavimento. A inclinação do bico da mangueira é
de 45°, sendo que a água sai com uma velocidade de 14.0 m/s.
Ka situação descrita, desprezando a resistência do ar. conseguiria
o bombeiro atingir o fogo? Considerar g = 9.8 m/s-.
€
V
L -
12.0 m
a) Sim, pois o alcance é de 20.0 m.
b) Não, pois o jato de água atinge o prédio apenas a urna altura
dc 6.3 m.
c) Não, pois o jato de água atinge o prédio apenas a uma altura
de 9.0 m.
d) Sim, só que o bombeiro deve diminuir o ângulo do bico da
mangueira.
e) Sim. pois a altura máxima que o jato de água atinge é superior
a 10,0 m.
Resolução: Analisemos inicialmente a projeção hori/.ontal do lança­
mento:
12
x = V0cos a . t 12 — 14 . cos 45° . t t = ———- s

271. Nesse mesmo instante, vejamos qual a altura atingida pela projeção
vertical:
y = yo -f Vo sen a . t ----- - gt2
y — 1,5 -f- 14 . sen 45° .
12 1
>
’= 1 ,5 + 2
VT
7 f~T
12
2 V T
y = 1,5 + 12 - 7 ,2 = 6,3 m .
2
4,9 .
. 9,8 .
144
49 . 2
V 7 /
y = 6,3 m
Portanto, o jato de água atingirá a altura de 6.3 m, insuficiente para
apagar o fogo localizado a 10,0 m de altura.
Resposta: alternativa b.
14. FEI — Um objeto voa numa trajetória retilínea, com velocidade
V = 200 m/s, numa altura H = 1 500 m do solo. Quando o objeto
passa exatamente na vertical de uma peça de artilharia, esta dis­
para um projétil, num ângulo de 60° com a horizontal. O projétil
atinge o objeto decorrido o intervalo de tempo At. Adotar g —
= 10 m/s2.
a) Calcular a intensidade tía velocidade de lançamento do projétil,
o) Calcular o menor intervalo de tempo At em que o projétil atinge
o objeto.
Resolução:
a) Para que o objeto seja atingido pelo projétil, a velocidade do objeto
deve ser igual ao vetor-^omponente-horizontal da velocidade do pro­
jétil.
Ou seja: V = V,v

272. 274
Assim: V —V0ls| = > V = V0cos 60° => V„
cos 60°
= > V 0 V0 — 400 m/s
b) A equação horária da projeção vertical do projétil será:
y = Vo , t ------— gt2= > y = Vo sen 60° . t ----- í- . 10t2=>
iy> 2 2
= > y — 400 . V ^ - t — 5t2= > y = 200 V"3t — 5t2
Quando o projétil atinge o objeto, y — 1 500 m.
Portanto, 1 500 = 200 T3t - 5t2 =>
= > t2—40 v"3í ■
+
- 300 = 0 =>
íU ar 4,6 s
112 ~
=
?64,6 s
O menor intervalo de tempo para a colisão será a menor das duas
raízes da equação acima, ou seja, t s 4,6 s
Resposta: O projétil será lançado com velocidade de 400 m/s, indo
atingir o corpo após, aproximadamente, 4,6 s.
1. UNIVERSIDADE IX) PARA­
NÁ — O esquema representa o
lançamento oblíquo de um corpo,
no vácuo, sob a ação da gravida­
de. Com relação a esse movi­
mento, qual a informação in­
correta?
a) A trajetória ACB descrita pelo móvel é um arco de parábola.
b) O móvel descreve a trajetória ACB com velocidade constante.
c) No ponto C a projeção vertical da velocidade é nula.

273. %(/?& 'ndârn 275
d) As projeções horizontais da velocidade instantânea são iguais em todos
os pontos da trajetória.
c) A intensidade da velocidade do móvel em B é igual à intensidade da
velocidade em A.
Uma bola é lançada para cima, em uma direção que forma um ângulo de
45° com a horizontal, com velocidade V. Despreze a resistência do ar. Enun­
ciado para as questões de 2 a 4.
2 UNIVERSIDADE DE MINAS GERAIS — A intensidade do vetor-com-
“> —
*
ponente-hori/.ontal Vx da velocidade V da bola c:
V
a) --------------- .
cos 45°
b) Vtg 45°.
c) Vcotg ^5°.
d) Vcos 45°.
V
c)
sen 45°
3. LNIVERSIDADE DE MINAS GERAIS A intensidade do vctor-com-
poncnte-vertical Vy da velocidade V da bola:
a) é constante.
b) é função do primeiro grau do tempo.
c) c função do segundo grau do tempo.
d) tem o mesmo sentido em qualquer instante.
e) é sempre diferente de zero.
4. UNIVERSIDADE DE MINAS GERAIS A aceleração da bola c:
a) horizontal c variável.
b) inclinada e constante.
c) vertical e constante.
d) inclinada c variável.
c) nula no ponto mais alto atingido pela bola.
5. MEDICINA DA SANTA CASA — Um canhão dispara uma bala com ân­
gulo de tiro de 40° cm relação ao solo. que é plano e horizontal. Despre­
zando a resistência do ar, pode-se dizer que. durante o movimento do pro­
jétil:
i) sua velocidade se mantém constante.
b) o vetor-componcnte-horizontal de sua velocidade se mantém constante.
c) sua aceleração muda de sentido, pois o vetor-componente-vertical da
velocidade muda de sentido.
il) o vctor-componente-horizontal de sua aceleração varia uniformemente.
»
’) a trajetória é percorrida com velocidade constante, cm módulo, embora
com direção variável.

274. 6. MEDICINA DE ITAJUBÁ — A velocidade inicial de um projétil forma
com a horizontal um ângulo de 60°, como mostra a figura abaixo. Despre­
zando a resistência do ar, qual dos segmentos seguintes melhor representa
a variação da velocidade do projétil entre o instante em que ele atinge o
ponto mais alto da trajetória e o instante de lançamento?
7. MACKENZIE — Durante um exercício de segurança contra incêndio, um
bombeiro segurou a mangueira dc água formando um ângulo de 45° com
a horizontal. Sabendo que a aceleração local da gravidade c de 10m/s2
c que a velocidade de saída do jato dc água é de 20m/s. pode-se afirmar
que serão atingidos objetos situados a uma distância horizontal do bico da
mangueira de:
a) 50,00 m.
b) 75,00 m.
c) 60.00 m.
d) 40,00 m.
c) 80 f l m.
8. MEDICINA DA SANTA CASA A figura seguinte representa a traje­
tória descrita por uma bola que sofre impactos sucessivos com o solo.
Sendo g a aceleração da gravidade, o intervalo dc tempo decorrido entre as
passagens pelas posições 1 e 2 é mcihor expresso por:

275. 9. UNIVERSIDADE DO PARÁ — Um projétil é lançado obliquamente, no
vácuo, com certa velocidade inicial, sob um ângulo de 30° com a horizon­
tal. Simultaneamente, um projétil idêntico c lançado com a mesma velo­
cidade inicial, porém sob um ângulo de 60° com a horizontal. Em um
ponto de altura H, o l.° projétil tem velocidade V. Em um ponto da mesma
altura, o segundo projétil terá velocidade igual a:
10. MEDICINA DE ITAJUBA — Uma bola está parada sobre o gramado dc.
um campo horizontal, na posição A. Um jogador chuta a bola para cima.
imprimindo-lhe uma velocidade V0 de intensidade 8,0 m/s, c que faz
com a horizontal um ângulo de 60°. como mostra a figura.
A bola sobe e desce, atingindo o solo novamente, na posição B. Despre­
zando a resistência do ar, qua! será a distância entre as posições A c B?
a) 2,4 m
b) 4,8 m
c) 2,8 m
d) 5,6 m
c) Um valor compreendido entre 2,4 m e 4,8 m.
II. MAPOFEI — Um canhão dispara projéteis de 20 kg com um ângulo de
30° cm relação à horizontal e com velocidade de 720 km/h. Qual o alcance
do projétil? Desprczam-se as resistepeias opostas pelo ar ao movimento.
(«cn 30° = cos 60° = 1/2; sen 60° ^ cos 30° = yJ/2; adote g = 10 m/s2.)
IJ UNIVERSIDADE DO PARÁ — Um objeto lançado vcrticalmente para
uma. no ar, atinge a altura de 280 m. Sc o objeto for lançado ohliquamcnte,
o seu ulcancc máximo será dc:
«) 560 m.
I>
) 280 m.
ü) 75 m.
d) 140 m.
c) 840 m.
a) v'TV.
2
d) 2V.
e) V.

276. 278
13. FEI — Um projétil é lançado do solo numa direção que forma o ângulo a
com a horizontal. Sabe-se que ele atinge uma altura máxima h mtí = 15 m
e que sua velocidade no ponto de altura máxima c V = 10 m/s. Deter­
minar a sua velocidade inicial c o ângulo a de lançamento. Adotar
g = 10 m/s'*.
14
. FAAP — Uma partícula é lançada obliquamente num plano vertical da
origem O de um referencial cartesiano xOv com velocidade de intensidade
10 m/s, a qual faz com o eixo Ox um ângulo de 60°. No mesmo instante,
é lançada verticalmcnte para cima uma outra partícula do ponto (100; 40/3).
onde as coordenadas são dadas em metros. Admitindo desprezíveis a
resistência do ar e a curvatura da superfície terrestre c considerando
g = 10 m/s2, determinar:
a) a intensidade da velocidade ca partícula lançada verticalmcnte para que
consiga encontrar a outra.
b) o tempo decorrido desde o instante dos lançamentos até o instante do
encontro.
15. FUNDAÇÃO CARLOS CHAGAS — Um canhão colocado no alto de uma
torre lança, horizontalmente, uma série de projéteis iguais, com velocidades
diferentes. Desprezando todos os atritos, qual dos seguintes gráficos me­
lhor representa a distância (D) alcançada pelos projéteis em função do tempo
(T) que os projeteis gastam para tocar o solo? Suponha que o solo também
0 0

277. 16. UNIVERSIDADE DE SANTA CATARINA — Duas bolinhas idênticas
A c B partem, ao mesmo tempo, de uma certa altura II do solo. sendo A
cm queda livre c B com uma velocidade V0, na direção horizontal. Pode­
mos afirmar que:
a) A chega primeiro ao solo.
b) B chega primeiro ao solo.
c) A ou B chega primeiro, dependendo da altura do lançamento.
d) A ou B chega primeiro, dependendo da velocidade inicial V
0 de B.
e) as duas chegam juntas ao solo.
17. FUNDAÇÃO CARLOS CHAGAS — Um avião voa à altura de 2 000 n,
paralclamcntc ao solo horizontal, com velocidade constante. Ele deixa cair
uma bomba que atinge o solo à distância de 1000 m da vertical de lança­
mento inicial da bomba.
Desprezando a resistência do ar, a velocidade do avião é um valor mais
próximo dc:
a) 50m/s. d) 2 000 m/s.
b) 150 m/s. e) 4 000 m/s.
c) 250 m/s.
18. PUC (SÀÜ PAULO) — Do alto dc uma torre são lançados, no mesmo
instante, dois corpos A e B. com velocidades iniciais iguais c inclinações
distintas <
I>
A= 30° e <
J>
„ ~ 45°. Observa-se que ambos atingem o solo (su­
posto horizontal) no mesmo ponto. Desprezando a resistência do ar, pode­
mos afirmar que a relação entre os tempos de queda tA
/tH
, respectivamente
dos corpos A c B. vale:
a) 1.
b) V
T
c) VT.
d)
el
v *
V3 '
x L
v? ■
Este enunciado refere-se aos testes 19 e 20.
O esquema representa uma correia que transporta minério, lançando-o no
recipiente R.
A velocidade da correia é constante e a aceleração da gravidade, 10 m/s2.

278. 230
19. PUC (SÃO PAULO) — Para que todo minério caia dentro do recipiente,
a velocidade V da correia, dada em m/s, deve satisfazer à desigualdade:
a) 2 < V < 3.
b) 2 < V < 5.
c) 1 < V < 3.
d) I < V < 4.
e) 1 < V < 5.
20. PUC (SÃO PAULO) — Se for aumentado o desnível entre a correia trans­
portadora e o recipiente R. o intervalo de variação das velocidades limites,
para que todo minério caia em R
a) permanece o mesmo, assim como os valores das velocidades limites.
b) permanece o mesmo, mas os valores das velocidades limites aumentam.
c) permanece o mesmo, mas os valores das velocidades limites diminuem.
d) aumenta,
c) diminui.
21. PUC (CAMPINAS) — Um avião, em vôo horizontal, a SOOOm de altura,
está bombardeando um destróier parado. A velocidade do avião é de
504 km/h. De quanto tempo dispõe o destróier para mudar seu curso de­
pois de uma bomba ter sido lançada?
a) 30 s
b) 40 s
c) 50 s
d) 20 s
e) n.d.a.
1. b 2. d 3. b 4. c 5. b 6. a
7. d 8. c 9. e 10. d
11. D —2 000V3 rn
12. a
13. V0 = 20 m/s: a = B0’.
14. a) 3v3m /s;
b) 20s.
15. e 16. e 17. a 18. d
19. d 20. e 21. b