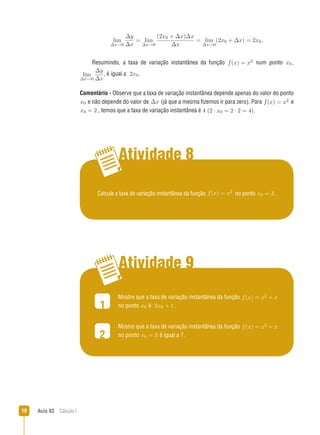
1) O documento apresenta os autores e informações sobre um curso de Cálculo I. 2) É fornecida a estrutura de governo federal e da universidade envolvida no curso. 3) A aula três introduz os conceitos de taxa de variação média e instantânea de funções.

1. André Gustavo Campos Pereira
Joaquim Elias de Freitas
Roosewelt Fonseca Soares
Cálculo ID I S C I P L I N A
Taxa de variação
Autores
aula
03

2. Copyright © 2007 Todos os direitos reservados. Nenhuma parte deste material pode ser utilizada ou reproduzida sem a autorização expressa da
UFRN - Universidade Federal do Rio Grande do Norte.
Divisão de Serviços Técnicos
Catalogação da publicação na Fonte. UFRN/Biblioteca Central “Zila Mamede”
Governo Federal
Presidente da República
Luiz Inácio Lula da Silva
Ministro da Educação
Fernando Haddad
Secretário de Educação a Distância – SEED
Carlos Eduardo Bielschowsky
Universidade Federal do Rio Grande do Norte
Reitor
José Ivonildo do Rêgo
Vice-Reitora
Ângela Maria Paiva Cruz
Secretária de Educação a Distância
Vera Lúcia do Amaral
Secretaria de Educação a Distância- SEDIS
Coordenadora da Produção dos Materiais
Marta Maria Castanho Almeida Pernambuco
Coordenador de Edição
Ary Sergio Braga Olinisky
Projeto Gráfico
Ivana Lima
Revisores de Estrutura e Linguagem
Eugenio Tavares Borges
Jânio Gustavo Barbosa
Thalyta Mabel Nobre Barbosa
Revisora das Normas da ABNT
Verônica Pinheiro da Silva
Revisoras de Língua Portuguesa
Janaina Tomaz Capistrano
Sandra Cristinne Xavier da Câmara
Revisores Técnicos
Leonardo Chagas da Silva
Thaísa Maria Simplício Lemos
Revisora Tipográfica
Nouraide Queiroz
Ilustradora
Carolina Costa
Editoração de Imagens
Adauto Harley
Carolina Costa
Diagramadores
Bruno de Souza Melo
Dimetrius de Carvalho Ferreira
Ivana Lima
Johann Jean Evangelista de Melo
Adaptação para Módulo Matemático
André Quintiliano Bezerra da Silva
Kalinne Rayana Cavalcanti Pereira
Thaísa Maria Simplício Lemos
Colaboradora
Viviane Simioli Medeiros Campos
Imagens Utilizadas
Banco de Imagens Sedis - UFRN
Fotografias - Adauto Harley
Stock.XCHG - www.sxc.hu
Pereira, André Gustavo Campos
Cálculo I / André Gustavo Campos Pereira, Joaquim Elias de Freitas, Roosewelt Fonseca Soares. – Natal,
RN: EDUFRN Editora da UFRN, 2008.
220 p.
1. Cálculo. 2. Funções reais. 3. Reta real. 4. Funções compostas. I. Freitas, Joaquim Elias de. II
Soares, Roosewelt Fonseca. III. Título.
ISBN: 978-85-7273-398-4
CDD 515
RN/UF/BCZM 2008/12 CDU 517.2/.3

3. Aula 03 Cálculo I
Apresentação
N
as aulas 1 (Limite de funções reais em um ponto) e 2 (Funções contínuas), estudamos
os conceitos de limite e continuidade de uma função que me respondem perguntas
sobre o que está acontecendo com a função em pontos específicos, como, por
exemplo, se está havendo saltos ou se está fluindo de modo contínuo. Entretanto, quando
estudamos um processo qualquer, gostaríamos de ter idéia do que podemos esperar dele
logo após o ponto em que o observamos. Esse tipo de questão começará a ser discutida
nesta aula por meio do estudo das taxas de variação tanto média quanto instantânea. Ao
final, introduziremos os conceitos e as propriedades da derivada de uma função, discussão
que se estenderá por mais algumas aulas.
Objetivos
Ao final desta aula, esperamos que você tenha entendido a
diferença entre taxa de variação média e instantânea, saiba
calculá-las e aplicá-las em alguns casos simples.

4. Aula 03 Cálculo I
Taxa de variação
O
que vem a sua mente quando alguém fala que a taxa de natalidade no Brasil cresceu?
Se cresceu é porque está nascendo mais gente, não é isso? Mas, como se mede isso?
Você tem que ter um período de tempo fixo para comparar, por exemplo, um ano.
Então, a taxa de natalidade seria expressa em número de nascimento por ano. Se em 2005
tivessem nascido 34.000 pessoas e em 2006 34.001, então, a taxa de natalidade cresceu.
Quando alguém diz que a taxa de juros ao mês é de 4%, o que ele está querendo dizer?
Isso quer dizer que se você deposita R$ 100,00 no início do mês, ao final você terá R$
104,00 na sua conta. Por quê?
O juro não é de 4% ao mês? Então, se você aumentasse R$ 100,00, dobraria o seu
dinheiro e ganharia 100% do valor investido, não é isso?
Montando uma regra de 3, teremos
Reais −− juros
100 −− 100%
x −− 4%
; resolvendo, teremos que
x = 4 reais, ou seja, ganhará R$ 4,00 de juros que, juntamente com os R$ 100,00 investidos,
você terá ao final do mês R$ 104,00.
Vemos nesses exemplos que uma taxa é qualquer relação entre uma quantidade de
referência (sob a qual você tem algum controle, pode escolher o tamanho, por exemplo: mês,
ano etc.) e alguma coisa que depende dessa referência (juros cobrados ao mês, número de
nascimentos ao ano etc.).
Na aula 8 (Funções I) de Pré-Cálculo, vimos que uma função f : A → B
x → y = f(x)
é uma
correspondência que a cada elemento de A associa um único elemento de B. Ou seja, fica
implícito que os elementos y , as quais serão escolhidos em B, dependerão dos valores x
do domínio, já que a relação é dada pela função e expressa por y = f(x). Por esse motivo,
muitos livros referem-se aos pontos do domínio como os valores da variável independente x
(você pode escolher o ponto) e os valores da imagem da f como sendo os valores da variável
dependente y = f(x) (depois de escolhido x, o valor do y é automaticamente determinado).
Então, se você quisesse calcular uma taxa, quem seria a referência, algo que você pode
escolher (um ano, um mês) ou algo sob o que você não tem controle, ou seja, uma coisa que
depende de outra quantidade para poder se fazer expressar?
Seria mais coerente aquilo sob o qual tem controle (que você pode escolher). Com isso
em mente, podemos começar a estudar taxa de variação.
A taxa de variação estuda e quantifica a razão entre o incremento da variável dependente
e o correspondente incremento da variável independente, isto é, o resultado da divisão do

5. Aula 03 Cálculo I
incremento da variável dependente pelo incremento da variável independente, que será o
ponto de partida para chegarmos ao conceito de Derivada, fundamental no Cálculo Diferencial.
A partir desse conceito, fica fácil definir Velocidade, Aceleração, Densidade de Massa, Lucro
Marginal, e muitos outros conceitos usados na Física, na Economia, na Biologia, nas Ciências
Sociais, enfim, em todas as áreas do conhecimento científico.
Nesta aula, vamos usar a notação y = f(x) para representar uma função, em que x
é a variável independente e y é a variável dependente de x, como discutido anteriormente.
Para representar um valor fixo da variável independente x, usamos a notação x0 , e y0 para
o valor de f(x0), isto é, y0 = f(x0).
Um incremento na variável independente x será denotado por ∆x (lemos delta x) e,
diferentemente do ∆x que estudamos em limites (veremos mais adiante por que essa
permissão não terá problema), poderá ser ∆x 0 ou ∆x 0. Da mesma forma, o valor
do conseqüente incremento da variável dependente, que representamos por ∆y (lemos
delta y), no ponto x = x0, é calculado do seguinte modo:
∆y = f(x0 + ∆x) − f(x0).
Observação 1 - Note que as expressões x = x0 + ∆x e y = y0 + ∆y podem ser reescritas
como ∆x = x − x0 e ∆y = y − y0. Os incrementos podem ser positivos, negativos ou
nulos, dependendo da posição relativa dos pontos inicial (antes do acréscimo) e final (depois
do acréscimo). Um incremento é positivo se o valor do ponto final for maior que o valor do
ponto inicial, é negativo se o valor do ponto final for menor que o valor do ponto inicial e
nulo se o valor do ponto final for igual ao do ponto inicial.
Exemplo 1
Considere a função y = f(x), sendo f(x) = x2 .
Vamos construir uma tabela na qual a variável independente x tem o valor fixo x0 = 1,
relacionando os incrementos ∆x = −0, 1; ∆x = −0, 01; ∆x = 0, 01 e ∆x = 0, 1 com
seus respectivos incrementos ∆y na variável dependente.
Vejamos o primeiro caso em que f(x) = x2
, x0 = 1 e ∆x = −0, 1. Desejamos obter
o incremento ∆y nessas condições. Como sabemos, ∆y é calculado do seguinte modo
∆y = f(x0 + ∆x) − f(x0).
Portanto,
∆y = f(1 + (−0, 1)) − f(1) = f(1 − 0, 1) − f(1),
∆y = f(0, 9) − f(1) = (0, 9)2 − 12,
∆y = 0, 81 − 1 = −0, 19,
∆y = −0, 19.
Resumindo, temos f(x) = x2, x0 = 1, ∆x = −0, 1 e ∆y = −0, 19.

6. Aula 03 Cálculo I
Atividade 1
Atividade 2
Atividade 3
Calcule o caso em que ∆x = 0, 1.
Calcule o caso em que ∆x = −0, 01.
Para ∆x = 0, 01, temos
∆y = f(x0 + ∆x) − f(x0) = f(1 + 0, 01) − f(1),
∆y = f(1, 01) − f(1) = (1, 01)2 − 12,
∆y = 1, 0201 − 1 = 0, 0201.
Resumindo, temos f(x) = x2, x0 = 1, ∆x = 0, 01 e ∆y = 0, 0201.
Devemos ter chegado ao seguinte resultado.
Tabela 1 - Relaciona incrementos ∆x e ∆y na função f(x) = x2
para x0 = 1.
∆x -0,1 -0,01 0,01 0,1
∆y -0,19 -0,0199 0,0201 0, 21
Construa outra tabela para a função f(x) = x2 na qual a variável independente
x tem o valor x0 = 2 , novamente relacionando os incrementos ∆x = −0, 1;
∆x = −0, 01; ∆x = 0, 01 e∆x = 0, 1 com seus respectivos incrementos ∆y.

7. Aula 03 Cálculo I
Atividade 4
Na Figura 1, a seguir, ilustramos os diferentes valores de ∆y obtidos quando utilizamos
dois valores distintos de x0 , e o mesmo valor de ∆x.
Legenda: ∆x ____
∆y ____
Figura 1 - a) Representação da função y = x2
, em x0 = 1, com ∆x = 1, e ∆y = 3; b) representação da função y = x2
, em
x0 = 2, com ∆x = 1, e ∆y = 5.
Utilizando gráfico da figura anterior, encontre os valores de ∆y quando
x0 = 1, e dois valores distintos de ∆x = −1 e ∆x = 1.

8. Aula 03 Cálculo I
Taxa de variação média
Considerando a função y = f(x) definimos como taxa de variação média de y entre
os valores x0 e x0 + ∆x o valor da razão entre a variação ∆y da variável dependente y, e
a variação ∆x da variável independente x, que denotamos por ∆y
∆x
.
Portanto, a taxa de variação média de y entre x0 e x0 + ∆x é definida como
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
.
Podemos calcular também a taxa de variação média de y = f(x) quando x varia entre
x0 e x1,
f(x1) − f(x0)
x1 − x0
;
basta que identifiquemos x0 e x0 + ∆x = x1.
Vamos tornar esse conceito mais claro utilizando o exemplo 2 a seguir.
Exemplo 2
Vamos calcular a taxa de variação média da mesma função y = x2
quando x varia entre
x0 = 1 e x1 = 2. Temos
f(x1) − f(x0)
x1 − x0
=
f(2) − f(1)
2 − 1
=
22 − 12
2 − 1
=
4 − 1
1
= 3.
Outra maneira seria; identificando, temos x0 = 1 e x0 + ∆x = x1 = 2 , ou seja,
∆x = 2 − 1 = 1 e, portanto,
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
=
f(1 + 1) − f(1)
1
=
f(2) − f(1)
1
=
4 − 1
1
= 3.
Resumindo, a taxa de variação média da função y = x2
quando x varia entre x0 = 1 e
x1 = 2 é igual a 3, isto é,
f(x1) − f(x0)
x1 − x0
= 3.
Exemplo 3
Vamos calcular a taxa de variação média da mesma função y = x2
quando x varia entre
x0 = 2 e x1 = 3. Temos
f(x1) − f(x0)
x1 − x0
=
f(3) − f(2)
3 − 2
=
32 − 22
1
=
9 − 4
1
= 5.

9. Aula 03 Cálculo I
Outra maneira seria: identificando, temos x0 = 2 e x0 + ∆x = x1 = 3, ou seja,
∆x = 3 − 2 = 1 e, portanto,
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
=
f(2 + 1) − f(2)
1
=
f(3) − f(2)
1
=
9 − 4
1
= 5.
Observe que a taxa de variação média vai depender dos pontos inicial e final que
estamos considerando, pois note que o ∆x foi igual a 1 em ambos os casos, mas a taxa de
variação média mudou.
Exemplo 4
Vamos calcular a taxa de variação média da função y = sen(x) quando x varia entre
x0 = 0 e x1 = π. Temos
f(π) − f(0)
π − 0
=
sen(π) − sen(0)
π
=
0 − 0
π
= 0 .
Exemplo 5
Vamos calcular a taxa de variação média da função y = sen(x) quando x varia entre
x0 = 0 e x1 =
π
2
. Temos
f(
π
2
) − f(0)
π
2
− 0
=
sen(
π
2
) − sen(0)
π
2
=
1 − 0
π
2
=
2
π
.
Você deve estar se perguntando depois desses dois últimos exemplos: “Como a taxa
de variação média de uma função pode ser maior em um intervalo pequeno do que num
intervalo maior que contém esse intervalo menor”? A resposta é bastante direta! Na taxa
de variação média, consideramos apenas valores da função nos pontos dados (final e
inicial), e não o comportamento geral da função. É como se apenas aqueles valores fossem
levados em consideração.
Podemos fazer a seguinte associação. Você chama um amigo para marcar a
quilometragem de uma corrida; você diz para ele que vai correr durante cinco minutos (em
volta de uma praça); quando o sinal tocar, você pára e então ele fará a medição do ponto de
partida até onde você parou pára calcular a quilometragem do número de voltas dadas e, por
fim, somar tudo. Entretanto, quando você deu a partida, ele adormeceu, você deu 1,2,3,4,...,
n voltas e ao toque do relógio ele acordou, mandou-lhe parar e fez a medição cujo resultado
foi 100m. Então ele olha em sua direção e diz: você correu apenas 100 metros em 5 minutos?
Ou seja, ele não viu o que aconteceu durante o período, só no início e no final.

10. Aula 03 Cálculo I
Atividade 5
Atividade 6
Atividade 7
Usando novamente a mesma função dos exemplos 1 e 2, y = x2
, e os cálculos
já obtidos, preenchamos as tabelas com mais uma entrada na qual escreveremos
as respectivas taxas de variação média.
Mostre que a taxa de variação média da função y = x3
quando x varia entre
x0 = 1 e x1 = 3 é igual a 13.
Recalcule as taxas de variação média da atividade anterior usando a equação1.
(Eq. 1)
Para a função f(x) = x2, temos que a taxa de variação média em um ponto (x0, y0),
onde y0 = f(x0) e ∆y = f(x0 + ∆x) − f(x0), é dada por
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
=
(x0 + ∆x)2 − (x0)2
∆x
,
∆y
∆x
=
x2
0 + 2x0∆x + (∆x)2 − x2
0
∆x
= 2x0 + ∆x.

11. Aula 03 Cálculo I
Taxa de variação instantânea
Considerando a função y = f(x), se olharmos para a taxa média entre x0 e x0 + ∆x
percebemos que a única quantidade passível de alteração é ∆x, ou seja, podemos ver
Fx0 (∆x) =
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
como uma função de ∆x.
Definimos como taxa de variação instantânea de y no ponto x0 o valor do limite de
Fx0 (∆x) quando ∆x tende a zero, que denotamos por
lim
∆x→0
Fx0 (∆x) = lim
∆x→0
∆y
∆x
= lim
∆x→0
f(x0 + ∆x) − f(x0)
∆x
Em termos de notação, lim
∆x→0
Fx0 (∆x) = lim
x→0
Fx0 (x). Ora, mas o último limite
sabemos calcular, caso exista!
Devemos mostrar que o limite tanto à direita quanto à esquerda existem e são iguais.
Lembra como se faz?
Tínhamos que tomar ∆x positivo e verificar se os valores Fx0 (0 − ∆x) e Fx0 (0 + ∆x)
sempre se aproximavam do mesmo valor quando ∆x tendia para zero. ∆x positivo
Fx0 (0 − ∆x) =
∆y
∆x
=
f(x0 − ∆x) − f(x0)
∆x
foi o que chamamos no início desta aula de
acréscimo negativo, e Fx0 (0 + ∆x) =
∆y
∆x
=
f(x0 + ∆x) − f(x0)
∆x
era o que estávamos
chamando de acréscimo positivo. Por isso, começamos esta aula já aceitando acréscimos
positivos e negativos sem muita distinção, pois no cálculo do limite anterior sabemos como
proceder sem problemas.
Para ajudar você a entender melhor o que isso significa, vamos começar com um
exemplo simples usando a mesma função vista anteriormente a fim de que possamos
observar a diferença entre a taxa de variação média e a taxa de variação instantânea.
Exemplo 6
A taxa de variação instantânea da função f(x) = x2 no ponto x0 é dada pelo limite
lim
∆x→0
∆y
∆x
= lim
∆x→0
f(x0 + ∆x) − f(x0)
∆x
= lim
∆x→0
(x0 + ∆x)2 − x2
0
∆x
,
lim
∆x→0
∆y
∆x
= lim
∆x→0
x2
0 + 2x0∆x + (∆x)2 − x2
0
∆x
= lim
∆x→0
2x0∆x + (∆x)2
∆x
,

12. Aula 03 Cálculo I10
Atividade 8
Atividade 9
1
2
lim
∆x→0
∆y
∆x
= lim
∆x→0
(2x0 + ∆x)∆x
∆x
= lim
∆x→0
(2x0 + ∆x) = 2x0 .
Resumindo, a taxa de variação instantânea da função f(x) = x2 num ponto x0 ,
lim
∆x→0
∆y
∆x
, é igual a 2x0 .
Comentário - Observe que a taxa de variação instantânea depende apenas do valor do ponto
x0 e não depende do valor de ∆x (já que a mesma fizemos ir para zero). Para f(x) = x2 e
x0 = 2 , temos que a taxa de variação instantânea é 4 (2 · x0 = 2 · 2 = 4).
Calcule a taxa de variação instantânea da função f(x) = x2
no ponto x0 = 3.
Mostre que a taxa de variação instantânea da função f(x) = x2 + x
no ponto x0 é 2x0 + 1 .
Mostre que a taxa de variação instantânea da função f(x) = x2 + x
no ponto x0 = 3 é igual a 7.

13. Aula 03 Cálculo I 11
Aplicações de taxa de variação
Velocidade
Vamos começar com um exemplo de uma corrida de automóvel em um circuito
automobilístico. A letra t representa o tempo, contado a partir da largada, s representa a
distância percorrida por um determinado carro participante da corrida. Desse modo, t é a
variável independente e s é a variável dependente de t, isto é, s = s(t). Vamos estabelecer
que no instante t = 0 a distância percorrida s(0) é nula, isto é, s(0) = 0. Vamos considerar
também que uma volta completa do circuito tenha 4,5 km e que esse carro completou a
primeira volta em 1 min e 30. Desejamos calcular a taxa de variação média
∆s
∆t
do carro
nesta primeira volta. Para facilitar os cálculos, usaremos o tempo da primeira volta na forma
1,5 min, em vez de 1 min e 30. Assim, com essas considerações, podemos escrever:
∆s
∆t
=
s(t + ∆t) − s(t)
∆t
=
s(0 + 1, 5) − s(0)
1, 5
=
4, 5 − 0
1, 5
= 3 .
Observe que podemos escrever a taxa de variação média levando em conta as unidades
de medida
∆s
∆t
=
4, 5km
1, 5min
= 3km/min . Quando a variável independente é o tempo t e
a variável dependente é o espaço s, a taxa de variação média é denominada de velocidade
média. Assim, para este exemplo, a velocidade média daquele determinado carro na primeira
volta foi de 3 km /min.
Velocidade média
Quando a variável independente é o tempo, a representamos pela letra t. Usualmente, a
variável dependente será denotada por s (t), que representa o espaço percorrido por um objeto
até o instante t. Nesse caso, a taxa de variação média é denominada de velocidade média.
Se ∆s
∆t
representa o deslocamento do objeto entre os instantes t e t + ∆t, isto é,
∆s = s(t + ∆t) − s(t), então, sua velocidade média, que denotamos por vm, nesse
intervalo de tempo é
vm =
∆s
∆t
=
s(t + ∆t) − s(t)
∆t
.

14. Aula 03 Cálculo I12
Velocidade média de um corpo em queda livre
Imaginemos um corpo em queda livre, como, por exemplo, um objeto que cai da janela
de um prédio. Sabemos por meio da Física que a equação de seu movimento, com velocidade
inicial nula, é dada por s(t) =
1
2
gt2 = 4, 9t2
, sendo s(t) o espaço percorrido pelo objeto em
queda livre até o instante t, considerando a aceleração da gravidade,
g = 9, 8m/seg2.
Vamos calcular a velocidade média,
∆s
∆t
, entre t0 e t0 + ∆t .
∆s
∆t
=
s(t0 + ∆t) − s(t0)
∆t
=
9,8
2 (t0 + ∆t)2 − 9,8
2 t2
0
∆t
,
∆s
∆t
=
9,8
2

t2
0 + 2t0∆t + (∆t)2

− 9,8
2 t2
0
∆t
,
∆s
∆t
=
4, 9t2
0 + 9, 8t0∆t + 4, 9(∆t)2 − 4, 9t2
0
∆t
,
∆s
∆t
= 9, 8t0 + 4, 9∆t .
Portanto, a velocidade média de um corpo em queda livre entre t0 e t0 + ∆t é
∆s
∆t
= 9, 8t0 + 4, 9∆t .
Velocidade instantânea
de um corpo em queda livre
Vamos agora calcular a velocidade instantânea, v(t0), de um corpo em queda livre
no instante t = t0 , que significa o valor limite das velocidades médias entre t0 e t0 + ∆t ,
calculadas no parágrafo anterior, quando ∆t tende a zero, ∆t → 0 , isto é,
v(t0) = lim
∆t→0
∆s
∆t
= lim
∆t→0
(9, 8t0 + 4, 9∆t),
v(t0) = lim
∆t→0
9, 8t0 + lim
∆t→0
4, 9∆t = 9, 8t0 + 0 ,
v(t0) = 9, 8t0 .
Comentário - Observe que a velocidade instantânea em um instante t0 pode ser vista como
a taxa de variação instantânea da função s(t) no ponto t0 .

15. Aula 03 Cálculo I 13
Atividade 10
1
2
3
4
5
Considere a função y = f(x), sendo f(x) = x2 + x.
Construa uma tabela na qual a variável independente x tem o valor fixo
x0 = 1 , relacionando os incrementos ∆x = −0, 1, ∆x = −0, 01,
∆x = 0, 01 e ∆x = 0, 1 com seus respectivos incrementos ∆y .
Considerando y = x2 + x, construa uma tabela na qual a variável
independente tem o valor x0 = 1, relacionando os incrementos
∆x = −0, 1 , ∆x = −0, 01 , ∆x = 0, 01 e ∆x = 0, 1 com os
respectivos ∆y e as taxas de variação média entre os valores x0
e x0 + ∆x .
Calcule a taxa de variação instantânea da função f(x) = x2 − x no
ponto x0 = 2 .
Em uma corrida de automóvel com um total de 62 voltas, realizada
em um circuito de rua com 4.500 metros de extensão, o primeiro
colocado completou a prova em 1 hora e 30 minutos. Encontre a sua
velocidade média em quilômetros por hora.
Calcule a velocidade instantânea, v(t0), de um corpo em queda livre
no instante t0 = 10s.

16. Aula 03 Cálculo I14
Resumo
1
2
Vimos que a palavra taxa significa uma relação existente entre duas grandezas,
uma sob a qual controle (independente) e outra que depende da primeira
(dependente). Dentre as taxas que podemos montar, estudamos as taxas de
variação média entre dois pontos x0 e x0 + ∆x, que representamos por
∆y
∆x
,
em que ∆y representa a variação da variável dependente y, e ∆x, a variação da
variável independente x. Já a taxa de variação instantânea no ponto x0 é obtida
da taxa de variação média entre os pontos x0 e x0 + ∆x fazendo ∆x tender
a zero, ou seja, lim
∆x→0
∆y
∆x
= lim
∆x→0
f(x0 + ∆x) − f(x0)
∆x
. Vimos que essas
taxas recebem nomes como velocidade média e velocidade instantânea quando a
função f representa o espaço percorrido e a variável x representa o tempo.
Auto-avaliação
Suponha que a função f represente o valor de suas economias no tempo. Suponha
que no tempo 0 você tenha R$ 100,00 e que, depois de 1 ano de retiradas e
depósitos, você chegou a R$ 110,00.
a) Qual a taxa de variação média de suas economias?
b) Para este cálculo, você levou em consideração todas as retiradas e todos os
depósitos ao longo do ano?
c) A taxa de variação foi positiva ou negativa?
d) O que isso significa (você tinha mais dinheiro antes ou agora)?
Com base na questão anterior, faça uma análise do sinal da taxa de variação com
relação à quantidade de dinheiro no início e no final do ano.

17. Aula 03 Cálculo I 15
Anotações
Referências
ANTON, Howard. Cálculo: um novo horizonte. 6. ed. Porto Alegre: Bookman, 2000. v 1.
SIMMONS, George F. Cálculo: com geometria analítica. São Paulo: McGraw-Hill, 1987. v 1.
THOMAS, George B. Cálculo. São Paulo: Addison Wesley, 2002.

18. Aula 03 Cálculo I16
Anotações