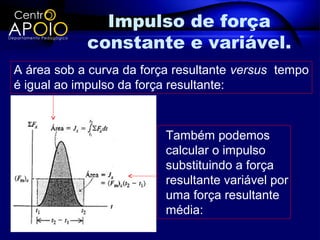
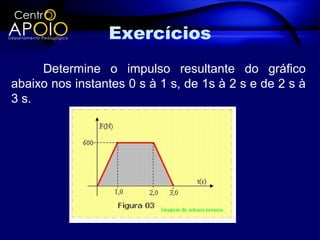
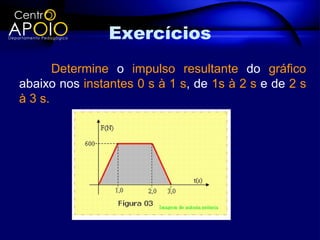
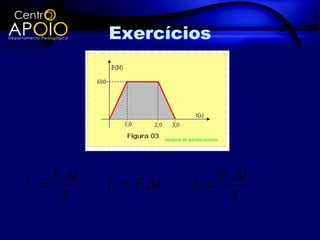
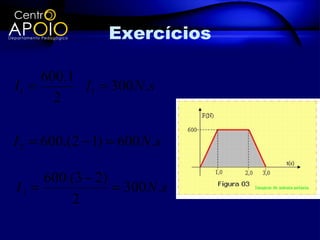
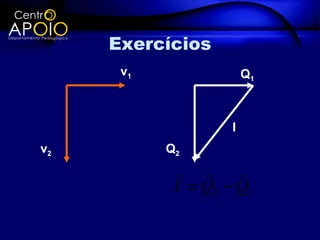
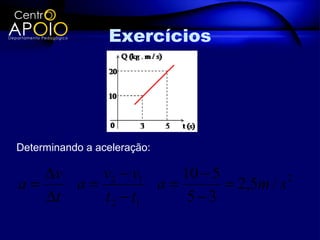
O documento discute a quantidade de movimento e seu relacionamento com impulso e força. Define quantidade de movimento como a massa multiplicada pela velocidade. Explica que impulso é igual à força aplicada durante um intervalo de tempo e é igual à variação da quantidade de movimento. Apresenta exercícios para exemplificar esses conceitos.

2. Em um jogo de futebol americano,
o que pode causar um dano maior:
a falta cometida por um jogador
leve e rápido sobre outro ou a falta
de um jogador com o dobro da
massa, mas que se move à
metade da velocidade?

3. Objetivos
• Definir Quantidade de movimento
• Definir impulso
• Aprender a relação entre impulso e quantidade de
movimento.
• Aprender a relação entre força e quantidade de
movimento

4. Quantidade de
movimento
A quantidade de movimento (Q), ou
momento linear, é uma grandeza física vetorial
definida por:
 
Q = m.v
Onde:
m _ massa do corpo [kg]
v_ velocidade do corpo [m/s]

5. Quantidade de
movimento
 
Q = m.v
A unidade de quantidade de movimento no
sistema internacional fica:
Kg.m/s

6. Exercícios
Uma partícula de massa m=0,20 kg possui,
num certo instante, velocidade v de módulo v = 10
m/s, direção horizontal e sentido da direita para a
esquerda. Determine nesse instante, ó módulo, a
direção e o sentido da quantidade de movimento da
partícula

7. Exercícios
Uma partícula de massa m=0,20 kg possui,
num certo instante, velocidade v de módulo v = 10
m/s, direção horizontal e sentido da direita para a
esquerda. Determine nesse instante, ó módulo, a
direção e o sentido da quantidade de movimento da
partícula

8. Exercícios
v
m
Q = m.v
 
Q = m.v Q = 0,20.10 = 2
Q = 2kg .m / s
A Quantidade de movimento tem módulo 2
kgm/s, direção horizontal e sentido da direita para a
esquerda

9. Exercícios
Um móvel de massa igual a 2 kg desloca-se
numa trajetória retilínea e possui quantidade de
movimento, em função do tempo, indicada pelo
gráfico.
Determine a aceleração sofrida pelo móvel

10. Exercícios
Um móvel de massa igual a 2 kg desloca-se
numa trajetória retilínea e possui quantidade de
movimento, em função do tempo, indicada pelo
gráfico.
Determine a aceleração sofrida pelo móvel

11. Exercícios
Sabendo que, Q=m.v, vamos determinar as velocidades
nos instantes t =3s e t=5s.
10 = 2.v1 20 = 2.v2
v1 = 5m / s v2 = 10m / s

12. Exercícios
Determinando a aceleração:
∆v v2 − v1 10 − 5
a= a= a= = 2,5m / s 2
∆t t 2 − t1 5−3

13. Impulso

14. Impulso
O impulso (I) é o resultado de uma força (F)
que atua sobre um corpo num dado intervalo de
tempo (∆t).
 
I = F .∆t

15. Impulso
O impulso (I) é o resultado de uma força (F)
que atua sobre um corpo num dado intervalo de
tempo (∆t). O impulso é uma grandeza vetorial
definida por:
 
I = F .∆t
Onde:
F_ força [N]
∆t_ intervalo de tempo [s]

16. Teorema impulso
Impulso de uma
Quantidade de
Força (I)
movimento

17. Exercícios
Um corpo de 2 kg de massa parte do
repouso com uma aceleração constante de 5 m/s².
Determine a intensidade de seu impulso durante
os 8 primeiros segundos.

18. Exercícios
Um corpo de 2 kg de massa parte do
repouso com uma aceleração constante de 5 m/s².
Determine a intensidade de seu impulso durante
os 8 primeiros segundos.
m a F

19. Exercícios
m a F
 
I = F .∆t
I = m.a.∆t I = 2.5.8 = 80
I = 80 N .s

20. Impulso de força
constante e variável.
A área sob a curva da força resultante versus tempo
é igual ao impulso da força resultante:
Também podemos
calcular o impulso
substituindo a força
resultante variável por
uma força resultante
média:

21. Exercícios
Determine o impulso resultante do gráfico
abaixo nos instantes 0 s à 1 s, de 1s à 2 s e de 2 s à
3 s.

22. Exercícios
Determine o impulso resultante do gráfico
abaixo nos instantes 0 s à 1 s, de 1s à 2 s e de 2 s
à 3 s.

23. Exercícios
F .∆t F .∆t
I1 = I 2 = F .∆t I3 =
2 2

24. Exercícios
600.1
I1 = I1 = 300 N .s
2
I 2 = 600.(2 − 1) = 600 N .s
600.(3 − 2)
I3 = = 300 N .s
2

25. Teorema impulso e
Quantidade de
Movimento
Um impulso de uma força resultante num
intervalo de tempo é igual a variação da quantidade
de movimento do corpo no mesmo intervalo de
tempo.
 
I = ∆Q

26. Teorema impulso e
Quantidade de
Movimento
Demonstração:
∆v
F = m.
F = m.a ∆t
F .∆t = m.(v − vo ) I = m.v − m.vo
I = Q − Qo I = ∆Q

27. Teorema impulso e
Quantidade de
Movimento
Representação vetorial de um impulso resultante.
Nesse caso, o Impulso provocou uma variação na
orientação do vetor Quantidade de Movimento.

28. Exercícios
Um corpo de massa m= 10 kg possui
velocidade v1 de direção horizontal e intensidade 3
m/s. Recebe um impulso I de uma força F que altera
sua velocidade inicial v1 para v2 , perpendicular a v1 e
de intensidade igual a 4 m/s. Determine o impulso I
dessa força F.

29. Exercícios
Um corpo de massa m= 10 kg possui
velocidade v1 de direção horizontal e intensidade 3
m/s. Recebe um impulso I de uma força F que altera
sua velocidade inicial v1 para v2 , perpendicular a v1 e
de intensidade igual a 4 m/s. Determine o impulso I
dessa força F.

30. Exercícios
v1 Q1
I
v2 Q2
  
I = Q2 − Q1

31. Exercícios
Q1
Q1 = m.v1 Q1 = 10.3
I Q1 = 30 N .s
Q2
Q2 = m.v2 Q2 = 10.4
  
I = Q2 − Q1 Q2 = 40 N .s

32. Exercícios
  
Q1
I = Q2 − Q1
2 2
I = Q1 + Q2
2
I
Q2
I = 40 + 30
2 2 2
I = 1600 + 900
2 I = 50 N .s

33. Exercícios
Q1
Sua direção θ com a horizontal
pode ser dada por:
I
Q2
Q2 tgθ =
Q1
30
tgθ = = 0,75 θ = arctg 0,75
40

34. Teorema impulso Variação da
Impulso de uma
Quantidade de Quantidade de
Força (I)
movimento Movimento (∆Q)

35. 2a Lei de Newton e
Quantidade de
movimento
Podemos reescrever a segunda Lei de Newton,
princípio fundamental da dinâmica, em termos de
Quantidade de movimento.
∆v
F = m.a F = m.
∆t

 ∆Q
F=
∆t

36. Exercícios
Um corpo exerce contato sobre outro corpo de
massa 2kg durante um intervalo de um milésimo de
segundo, alterando sua velocidade de 2 m/s para 10
m/s. Determine a força resultante média que o
primeiro corpo exerce sobre o segundo corpo.

37. Exercícios
Um corpo exerce contato sobre outro corpo de
massa 2kg durante um intervalo de um milésimo de
segundo, alterando sua velocidade de 2 m/s para 10
m/s. Determine a força resultante média que o
primeiro corpo exerce sobre o segundo corpo.

38. Exercícios

 ∆Q
F=
∆t
Q − Qo 2.10 − 2.2
F= F=
∆t 0,001
F = 16000 N

39. Bibliografia:
Ramalho, Nicolau e Toledo. Os fundamentos da
física. Mecânica, ed. Moderna. 7a edição.
Halliday, Resnick, Walker. Fundamentos de física.
Mecânica, ed. LTC, 3a edição.