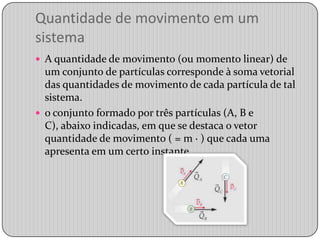
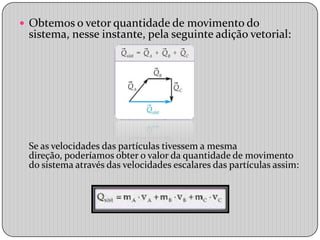
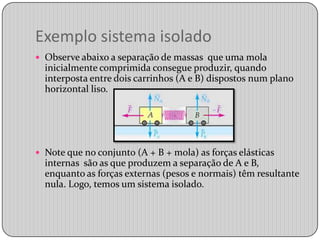
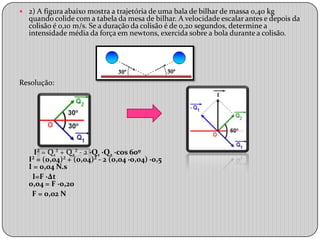
1) O documento discute a quantidade de movimento em sistemas, definindo-a como o produto da massa de uma partícula pela sua velocidade e como a soma vetorial das quantidades de movimento de cada partícula em um sistema. 2) É explicado que a quantidade de movimento de um sistema isolado é conservada, ou seja, sua quantidade de movimento total no início é igual ao final. 3) Exemplos ilustram a conservação da quantidade de movimento em sistemas isolados e durante colisões entre partículas.

1. Ana Carolina , nº1Mariana Mendes, nº21Conservação da quantidade de movimento

2. Quantidade de movimentoDefine-se a quantidade de movimento (q), (ou p) como o produto da velocidade de uma partícula pela sua massa:A relevância dessa grandeza física (a quantidade de movimento) foi percebida e, conseqüentemente, introduzida por Newton.

3. Quantidade de movimento em um sistemaA quantidade de movimento (ou momento linear) de um conjunto de partículas corresponde à soma vetorial das quantidades de movimento de cada partícula de tal sistema.o conjunto formado por três partículas (A, B e C), abaixo indicadas, em que se destaca o vetor quantidade de movimento ( = m · ) que cada uma apresenta em um certo instante.

4. Obtemos o vetor quantidade de movimento do sistema, nesse instante, pela seguinte adição vetorial:Se as velocidades das partículas tivessem a mesma direção, poderíamos obter o valor da quantidade de movimento do sistema através das velocidades escalares das partículas assim:

5. Sistema isoladoEm um sistema podem agir forças internas e externas. São chamadas de forças internas aquelas que são trocadas entre as partículas do sistema. Por constituírem pares ação-reação, o impulso total devido às forças internas sempre será nulo.Uma força é classificada como externa quando é exercida no sistema pelo meio externo a ele. Essa força pode ser de ação a distância (força de campo) ou de contato.O sistema será considerado isolado quando: a) nenhuma força externa atuar, ou a resultante das forças externas for nula;b) as forças externas forem desprezíveis, se comparadas com as forças internas;c) a interação com o meio externo tiver uma duração muito pequena ( 0).

6. Exemplo sistema isoladoObserve abaixo a separação de massas que uma mola inicialmente comprimida consegue produzir, quando interposta entre dois carrinhos (A e B) dispostos num plano horizontal liso.Note que no conjunto (A + B + mola) as forças elásticas internas são as que produzem a separação de A e B, enquanto as forças externas (pesos e normais) têm resultante nula. Logo, temos um sistema isolado.

7. Conservação da quantidade de movimentoA quantidade de movimento de um sistema isolado sempre se conserva, qualquer que seja a interação praticada pelos corpos do sistema.Qinicial= Qfinal

8. ColisõesPara um choque frontal, podemos escrever a equação de conservação de quantidade de movimento do sistema usando velocidades escalares, ou seja, atribuindo um sinal algébrico às velocidades das partículas de acordo com a orientação (positiva) definida para a trajetória.

9. ImpulsoO impulso da resultante das forças sobre uma partícula, num certo intervalo de tempo, é igual à variação da quantidade de movimento da partícula nesse mesmo intervalo de tempo.

10. Exercícios resolvidos conservação da quantidade de movimento1) Uma peça de artilharia de massa 2 toneladas dispara uma bala de 8 kg. A velocidade do projétil no instante em que abandona a peça é 250 m/s. Calcule a velocidade do recuo da peça, desprezando a ação de forças externas. Resolução: vP- velocidade da peçavB - velocidade da balaQantes= Qdepois0 = - vp ·2000 + 8 ·2502000 vp = 2000vp = 1 m/s

11. 2) A figura abaixo mostra a trajetória de uma bala de bilhar de massa 0,40 kg quando colide com a tabela da mesa de bilhar. A velocidade escalar antes e depois da colisão é 0,10 m/s. Se a duração da colisão é de 0,20 segundos, determine a intensidade média da força em newtons, exercida sobre a bola durante a colisão.Resolução: I² = Q1² + Q2² - 2 ·Q1 ·Q2 ·cos 60ºI² = (0,04)² + (0,04)² - 2 (0,04 ·0,04) ·0,5I = 0,04 N.sI=F ·Δt0,04 = F ·0,20 F = 0,02 N

12. Exercício resolvido impulsoAo dar um chute na bola, num jogo de futebol, um jogador aplica um força de intensidade 6,0 · 10² N sobre a bola, durante um intervalo de tempo de 1,5 · 10-1 s. Determine a intensidade do impulso da força aplicada pelo jogador. F = 6,0 · 10² N t= 1,5 · 10-1s I= F. Δt I= 90 N.s