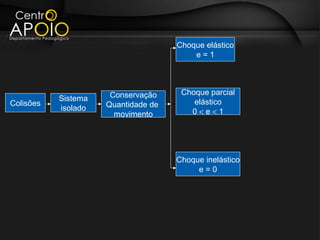
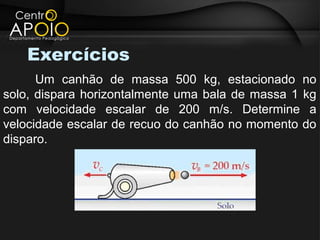
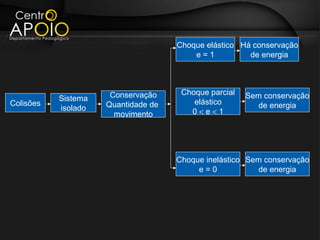
O documento aborda o conceito de colisões, definindo-as como interações entre corpos que envolvem troca de quantidade de movimento e energia. Explica os diferentes tipos de colisão (elástica, parcialmente elástica e inelástica) e a conservação da quantidade de movimento em sistemas isolados. Além disso, apresenta exemplos e exercícios para ilustrar a aplicação dos conceitos discutidos.

1. Colisões

2. Objetivos
• Definir colisão.
• Aprender os tipos de colisão.
• Aprender o que é conservação da quantidade de
movimento.
• Aplicar os conceitos de Quantidade de movimento e
impulso em colisões.

3. Colisões
• Uma colisão é uma interação com duração limitada
entre dois ou mais corpos.
ex: Bola de bilhar, acidente de carro e meteoro e a
terra.
• Numa Colisão há troca de Quantidade de
movimento e energia em conseqüência de sua
interação.
• Veremos colisões envolvendo apenas dois corpos
que estarão livres de qualquer força externa, ou
seja, a força externa será menor que as forças
envolvidas nas colisões e portanto desprezíveis.

4. Colisões

5. Conservação da
Quantidade de
movimento
• O conceito de momento linear (Quantidade de
movimento) é particularmente importante
quando ocorre interação entre dois ou mais
corpos.
• Fint = a força que uma partícula de um sistema
exerce sobre a outra.
• Fext = a força exercida por um corpo no exterior
do sistema sobre uma parte interna ou sobre
algum corpo no interior do sistema.

6. Conservação da
Quantidade de movimento
Nenhuma força externa atua sobre o sistema composto pelos
dois astronautas, por isso seu momento linear total é
conservado.
y y
sobre A sobre B
As forças que os astronautas exercem mutuamente
formam um par de ação e reação.

7. Conservação da
Quantidade de movimento
Em qualquer sistema isolado de ações
externas, o impulso total sobre o sistema será
sempre nulo, ou seja, no sistema não haverá
variação da quantidade de movimento total.

∆Q = 0

8. Conservação da
Quantidade de movimento
A quantidade de movimento de um sistema
isolado sempre se conserva, qualquer que seja a
ação praticada pelos corpos do sistema.
Q = Qo

9. Conservação da
Quantidade de movimento
Podemos dizer também que a quantidade
de movimento total do sistema isolado é
constante.
Qantes = Qdepois

10. Sistema Conservação
Colisões Quantidade de
isolado
movimento

11. Tipos de colisão
• Se a energia total não for alterada pela colisão,
então Ec do sistema é conservada (mesma antes e
depois da colisão). Tal colisão é chamada Colisão
Elástica. Ex: meteoro e bilhar.
• Em colisões do cotidiano, alguma energia é
transferida da Ec para outras formas de energia,
como sonora e térmica. Dessa forma a energia total
do sistema não se conserva. Tais colisões podem
ser parcialmente elásticas e inelásticas. Ex: Colisão
de automóveis.

12. Tipos de colisão
Coeficiente de restituição (e).
Determina se a colisão é do tipo elástica, parcialmente
elástica ou inelástica, seus valores variam entre 0 e 1.
velocidade relativa depois do choque
e=
velocidade relativa antes do choque

13. Tipos de colisão
Colisão elástica:
e=1
Colisão parcialmente elástica:
0<e<1
Colisão inelástica:
e=0

14. Tipos de colisão
Atenção!
Após um choque inelástico, os corpos permanecem
unidos.

15. Choque elástico
e=1
Conservação Choque parcial
Sistema elástico
Colisões Quantidade de
isolado 0<e<1
movimento
Choque inelástico
e=0

16. Exercícios
Um carrinho de massa 1,0 kg move-se sobre um
piso horizontal, com velocidade de 4,0 m/s, em direção a
outro carrinho de massa 3,0 kg, inicialmente em
repouso. Após o choque, eles permanecem unidos.
Determine a intensidade da quantidade de movimento
dos carrinhos e suas velocidades após o choque.

17. Exercícios
Um carrinho de massa 1,0 kg move-se sobre um
piso horizontal, com velocidade de 4,0 m/s, em direção a
outro carrinho de massa 3,0 kg, inicialmente em
repouso. Após o choque, eles permanecem unidos.
Determine a intensidade da quantidade de movimento
dos carrinhos e suas velocidades após o choque.

18. Exercícios
Qantes = Qdepois
m
Q = m1.v1 Q = 1.4 = 4kg
s
m1.v1 + m2 .v2 = (m1 + m2 ).v 1.4 + 3.0 = (1 + 3).v
v = 1m / s

19. Exercícios
Um canhão de massa 500 kg, estacionado no
solo, dispara horizontalmente uma bala de massa 1 kg
com velocidade escalar de 200 m/s. Determine a
velocidade escalar de recuo do canhão no momento do
disparo.

20. Exercícios
Um canhão de massa 500 kg, estacionado no
solo, dispara horizontalmente uma bala de massa 1 kg
com velocidade escalar de 200 m/s. Determine a
velocidade escalar de recuo do canhão no momento do
disparo.

21. Exercícios
Qantes = Qdepois
m1.v1 + m2 .v2 = m1.v1 '+ m2 .v2 ' 500.0 + 1.0 = 500.v1 '+1.200
200
v1 ' = v1 ' = 0,4m / s
500

22. Exercícios
O gráfico abaixo representa as velocidades
escalares de duas pequenas esferas, A e B, que
realizam uma colisão frontal (com faixa de duração
em destaque no gráfico). Determine o coeficiente
de restituição entre A e B, e a relação entre suas
massas.

23. Exercícios
O gráfico abaixo representa as velocidades
escalares de duas pequenas esferas, A e B, que
realizam uma colisão frontal (com faixa de duração
em destaque no gráfico). Determine o coeficiente
de restituição entre A e B, e a relação entre suas
massas.

24. Exercícios
velocidade relativa depois do choque
e=
velocidade relativa antes do choque
v1 '− v 2 ' 2−0
e= e=
v1 − v 2 0−2
2
e=
−2 e =1

25. Exercícios
Qantes = Qdepois
m1.v1 + m2 .v2 = m1.v1 '+ m2 .v2 '
m1.2 + m2 .0 = m1.0 + m2 .2
m1 2
= =1
m2 2

26. Exercícios
Suponha que você tenha de escolher agarrar
uma bola de 0.5 kg que desloca-se com uma
velocidade de 4 m/s ou uma bola de 0,1 kg com v =
20 m/s. Qual das duas bolas seria mais fácil agarrar?

27. Exercícios
Suponha que você tenha de escolher agarrar
uma bola de 0.5 kg que desloca-se com uma
velocidade de 4 m/s ou uma bola de 0,1 kg com v =
20 m/s. Qual das duas bolas seria mais fácil agarrar?

28. Exercícios
Q1 = m1.v1 Q2 = m2 .v2
Q1 = 0,5.4 Q2 = 0,1.20
m m
Q1 = 2kg Q2 = 2kg
s s

29. Exercícios
Ambas as bolas tem mesma quantidade de
movimento, isso significa que o impulso durante a
colisão é o mesmo, ou seja, para os dois casos o
intervalo de tempo para segurar a bola é o mesmo.

30. Exercícios 2
mv 2 m2 v 2
Ec1 = 1 1 Ec 2 =
2 2
2
0,5.4 2 0,1.20
Ec1 = Ec 2 =
2 2
Ec1 = 4 J Ec 2 = 20 J

31. Exercícios
A energia cinética do segundo caso é 5 vezes maior
que a primeira, pelo teorema trabalho energia, neste
caso a bola faz a mão percorrer uma distancia 5 vezes
maior no mesmo intervalo de tempo.
2
m.v
Fmédia .d =
2

32. Choque elástico Há conservação
e=1 de energia
Conservação Choque parcial Sem conservação
Sistema elástico
Colisões Quantidade de de energia
isolado 0<e<1
movimento
Choque inelástico Sem conservação
e=0 de energia

33. Bibliografia:
Ramalho, Nicolau e Toledo. Os fundamentos da
física. Mecânica, ed. Moderna. 7a edição.
Halliday, Resnick, Walker. Fundamentos de física.
Mecânica, ed. LTC, 3a edição.