Um próton é acelerado a 3,6 × 1015 m/s2 em um acelerador de partículas. Sua velocidade inicial é de 2,4 × 107 m/s e se desloca 3,5 cm. Sua velocidade final é de 2,9 × 107 m/s e o aumento de sua energia cinética é de 2,1 × 10-13 J. A energia cinética de um foguete Saturno V e uma espaçonave acoplada com massa total de 2,9 × 105 kg quando atingiram 11,2 km/s era de 1,

1. ·1 Um próton (massa m = 1,67 H 10-27
kg) está sendo acelerado, em linha reta, a 3,6 × 1015
m/s2
em um
acelerador de partículas. Se o próton tem velocidade inicial de 2,4 × 107
m/s e se desloca 3,5 cm,
determine (a) a velocidade e (b) o aumento da energia cinética do próton.
·2 Se um foguete Saturno V e uma espaçonave Apolo acoplada ao foguete tinham massa total de 2,9 × 105
kg, qual era a energia cinética quando os objetos atingiram uma velocidade de 11,2 km/s?
1. (a) From Table 2-1, we have v v a x2
0
2
2= + Δ . Thus,
( ) ( )( )
2
2 7 15 2 7
0 2 2.4 10 m/s 2 3.6 10 m/s 0.035 m 2.9 10 m/s.v v a x= + Δ = × + × = ×
(b) The initial kinetic energy is
( )( )
22 27 7 13
0
1 1
1.67 10 kg 2.4 10 m/s 4.8 10 J.
2 2
iK mv − −
= = × × = ×
The final kinetic energy is
( )( )
22 27 7 131 1
1.67 10 kg 2.9 10 m/s 6.9 10 J.
2 2
fK mv − −
= = × × = ×
The change in kinetic energy is ΔK = 6.9 × 10–13
J – 4.8 × 10–13
J = 2.1 × 10–13
J.
2. With speed v = 11200 m/s, we find
2 5 2 131 1
(2.9 10 kg) (11200 m/s) 1.8 10 J.
2 2
K mv= = × = ×
·8 Um bloco de gelo flutuante é colhido por uma correnteza que aplica ao bloco uma força = (210 N) –
(150 N) fazendo com que o bloco sofra um deslocamento = (15 m) – (12 m) . Qual é o trabalho
realizado pela força sobre o bloco durante o deslocamento?
3
ˆ ˆ ˆ ˆ(210 N)i (150 N) j (15 m)i (12 m)j (210 N)(15 m) ( 150 N)( 12 m)
5.0 10 J.
W F d ⎡ ⎤ ⎡ ⎤= ⋅ = − ⋅ − = + − −
⎣ ⎦ ⎣ ⎦
= ×
··11 Uma força de 12,0 N e com orientação fixa realiza trabalho sobre uma partícula que sofre um
deslocamento = (2,00 – 4,00 + 3,00 ) m. Qual é o ângulo entre a força e o deslocamento se a
variação da energia cinética da partícula é (a) +30,0 J e (b) –30,0 J?
cosK W F d Fd φΔ = = ⋅ = .
In addition, 12 NF = and 2 2 2
(2.00 m) ( 4.00 m) (3.00 m) 5.39 md = + − + = .
(a) If 30.0 JKΔ = + , then
1 1 30.0 J
cos cos 62.3
(12.0 N)(5.39 m)
K
Fd
φ − − ⎛ ⎞Δ⎛ ⎞
= = = °⎜ ⎟⎜ ⎟
⎝ ⎠ ⎝ ⎠
.

2. (b) 30.0 JKΔ = − , then
1 1 30.0 J
cos cos 118
(12.0 N)(5.39 m)
K
Fd
φ − − ⎛ ⎞Δ −⎛ ⎞
= = = °⎜ ⎟⎜ ⎟
⎝ ⎠ ⎝ ⎠
.
··14 A Fig. 7-27 mostra uma vista superior de três forças horizontais agindo sobre uma caixa que estava
inicialmente em repouso e passou a se mover em um piso sem atrito. Os módulos das forças são F1 = 3,00
N, F2 = 4,00 N, e F3 = 10,0 N e os ângulos indicados são θ2 = 50,0° e θ3 = 35,0°. Qual é o trabalho total
realizado sobre a caixa pelas três forças nos primeiros 4,00 m de deslocamento?
Figura 7-27 Problema 14.
14. The forces are all constant, so the total work done by them is given by W F x= net Δ ,
where Fnet is the magnitude of the net force and Δx is the magnitude of the displacement.
We add the three vectors, finding the x and y components of the net force:
net 1 2 3
net 2 3
sin50.0 cos35.0 3.00 N (4.00 N)sin35.0 (10.0 N)cos35.0
2.13N
cos50.0 sin35.0 (4.00 N) cos50.0 (10.0 N)sin35.0
3.17 N.
x
y
F F F F
F F F
= − − °+ ° = − − °+ °
=
= − °+ ° = − ° + °
=
The magnitude of the net force is
2 2 2 2
net net net (2.13 N) (3.17 N) 3.82 N.x yF F F= + = + =
The work done by the net force is
net (3.82 N)(4.00m) 15.3 JW F d= = =
where we have used the fact that d Fnet|| (which follows from the fact that the canister
started from rest and moved horizontally under the action of horizontal forces — the
resultant effect of which is expressed by Fnet ).

3. ·17 Um helicóptero levanta verticalmente, por meio de um cabo, uma astronauta de 72 kg até uma altura
15 m acima da superfície do oceano. A aceleração da astronauta é g/10. Qual é o trabalho realizado
sobre a astronauta (a) pela força do helicóptero e (b) pela força gravitacional? Imediatamente antes de a
astronauta chegar ao helicóptero, quais são (c) sua energia cinética e (d) sua velocidade?
Wa = −(50 N)(0.50 m) = −25 J
(the minus sign arises from the fact that the pull from the rope is anti-parallel to the
direction of motion of the block). Thus, the kinetic energy would have been 25 J greater
if the rope had not been attached (given the same displacement).
··19 Na Fig. 7-30, um bloco de gelo escorrega para baixo em uma rampa sem atrito com uma inclinação θ
= 50o
enquanto um operário puxa o bloco (por meio de uma corda) com uma força r que tem um módulo
de 50 N e aponta para cima ao longo da rampa. Quando o bloco desliza uma distância d = 0,50 m ao
longo da rampa, sua energia cinética aumenta 80 J. Quão maior seria a energia cinética se o bloco não
estivesse sendo puxado por uma corda?
11
( )
10
F mg ma F m g a mg− = ⇒ = + = ,
·34 Um tijolo de 10 kg se move ao longo de um eixo x. A Fig. 7-38 mostra a aceleração do tijolo em
função da posição. A escala vertical do gráfico é definida por as = 20,0 m/s2
. Qual é o trabalho total
realizado sobre o tijolo pela força responsável pela aceleração quando o tijolo se desloca de x = 0 para
x = 8,0 m?
Figura 7-38 Problema 34.
α = = −20
8 0
2 5 2m / s
m
s
2
.
. .
2
2 2 2
0 0
(10 kg)(2.5 s )
(8.0 m) 8.0 10 J.
2 2
f fx x
f
m
W F dx m x dx x
α
α
−
= = = = = ×∫ ∫
2
4 411 11 (72 kg)(9.8 m/s )(15 m)
1.164 10 J 1.2 10 J
10 10
F
mgd
W Fd= = = = × ≈ × .(a)
(b) 2 4 4
(72 kg)(9.8 m/s )(15 m) 1.058 10 J 1.1 10 Jg gW F d mgd= − = − = − = − × ≈ − ×
(c) 4 4 3 3
net 1.164 10 J 1.058 10 J 1.06 10 J 1.1 10 JF gW W W= + = × − × = × ≈ × .
(d) Since K mv= 1
2
2
, her final speed is
3
2 2(1.06 10 J)
5.4 m/s
72 kg
K
v
m
×
= = = .
Note: For a general upward acceleration a, the net work done is
net ( )F g gW W W Fd F d m g a d mgd mad= + = − = + − = .
Since 2
net / 2,W K mv= Δ = by the work-kinetic energy theorem, the speed of the
astronaut would be 2v ad= , which is independent of the mass of the astronaut.

4. ·35 A força a que uma partícula está submetida aponta ao longo de um eixo x e é dada por F = F0(x/x0 –
1). Determine o trabalho realizado pela força ao mover a partícula de x = 0 a x = 2x0 de duas formas: (a)
plotando F(x) e medindo o trabalho no gráfico; (b) integrando F(x).
35. Given a one-dimensional force ( )F x , the work done is simply equal to the area under
the curve: ( )
f
i
x
x
W F x dx= ∫ .
(a) The plot of F(x) is shown above. Here we take x0 to be positive. The work is negative
as the object moves from x x x= =0 0to and positive as it moves from x x x x= =0 02to .
Since the area of a triangle is (base)(altitude)/2, the work done from x x x= =0 0to is
1 0 0( )( ) / 2W x F= −
and the work done from x x x x= =0 02to is
2 0 0 0 0 0(2 )( ) / 2 ( )( ) / 2W x x F x F= − = .
The total work is the sum of the two: 1 2 0 0 0 0
1 1
0
2 2
W W W F x F x= + = − + = .
(b) The integral for the work is
0
0
2
2
2
0 00
0 0 0
1 0.
2
x
x x x
W F dx F x
x x
⎛ ⎞ ⎛ ⎞
= − = − =⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠
∫
·36 Um bloco de 5,0 kg se move em linha reta em uma superfície horizontal, sem atrito, sob a influência
de uma força que varia com a posição, como é mostrado na Fig. 7-39. A escala vertical do gráfico é
definida por Fs = 10,0 N. Qual é o trabalho realizado pela força quando o bloco se desloca da origem até
x = 8,0 cm?
Figura 7-39 Problema 36.

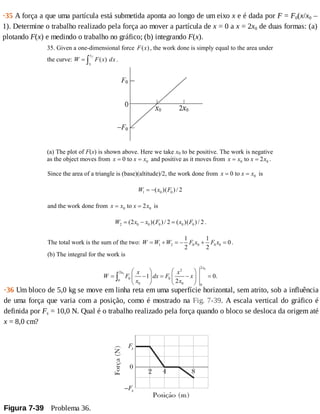
5. 36. From Eq. 7-32, we see that the “area” in the graph is equivalent to the work done.
Finding that area (in terms of rectangular [length × width] and triangular
[1
2 base height]× areas) we obtain
0 2 2 4 4 6 6 8 (20 10 0 5) J 25 J.x x x xW W W W W< < < < < < < <= + + + = + + − =
·43 Uma força de 5,0 N age sobre um corpo de 15 kg inicialmente em repouso. Calcule o trabalho
realizado pela força (a) no primeiro, (b) no segundo e (c) no terceiro segundo, assim como (d) a potência
instantânea da força no fim do terceiro segundo.
43. (a) The power is given by P = Fv and the work done by F from time t1 to time t2 is
given by
2 2
1 1
t t
t t
W Pdt Fvdt= =∫ ∫ .
Since F is the net force, the magnitude of the acceleration is a = F/m, and, since the
initial velocity is v0 0= , the velocity as a function of time is given by
v v at F m t= + =0 ( ) . Thus,
2
1
2 2 2 2
2 1
1
( / ) ( / )( ).
2
t
t
W F m t dt F m t t= = −∫
For t1 0= and 2 1.0s,t =
2
21 (5.0 N)
(1.0 s) = 0.83 J.
2 15 kg
W
⎛ ⎞
= ⎜ ⎟
⎝ ⎠
(b) For 1 1.0s,t = and 2 2.0s,t =
2
2 21 (5.0 N)
[(2.0 s) (1.0 s) ] 2.5 J.
2 15 kg
W
⎛ ⎞
= − =⎜ ⎟
⎝ ⎠
(c) For 1 2.0st = and 2 3.0s,t =
2
2 21 (5.0 N)
[(3.0 s) (2.0 s) ] 4.2 J.
2 15 kg
W
⎛ ⎞
= − =⎜ ⎟
⎝ ⎠
(d) Substituting v = (F/m)t into P = Fv we obtain P F t m= 2
for the power at any time t.
At the end of the third second P
(5.0 N) (3.0 s)
15 kg
5.0 W.
2
=
F
HG I
KJ =

6. ·44 Um esquiador é puxado por uma corda para o alto de uma encosta que faz um ângulo de 12° com a
horizontal. A corda se move paralelamente à encosta com velocidade constante de 1,0 m/s. A força da
corda realiza 900 J de trabalho sobre o esquiador quando este percorre uma distância de 8,0 m encosta
acima. (a) Se a velocidade constante da corda fosse 2,0 m/s, que trabalho a força da corda teria realizado
44. (a) Since constant speed implies ΔK 0,= we require W Wa g= − , by Eq. 7-15. Since
Wg is the same in both cases (same weight and same path), then 2
9.0 10aW = × J just as it
was in the first case.
(b) Since the speed of 1.0 m/s is constant, then 8.0 meters is traveled in 8.0 seconds.
Using Eq. 7-42, and noting that average power is the power when the work is being done
at a steady rate, we have
2900 J
1.1 10 W.
8.0 s
W
P
t
= = = ×
Δ
(c) Since the speed of 2.0 m/s is constant, 8.0 meters is traveled in 4.0 seconds. Using Eq.
7-42, with average power replaced by power, we have
900 J
4.0 s
W
P
t
= =
Δ
= 225 W 2
2.3 10 W≈ × .
··47 Uma máquina transporta um pacote de 4,0 kg de uma posição inicial i = (0,50 m) + (0,75 m) +
(0,20 m) em t = 0 até uma posição final f = (7,50 m) + (12,0 m) + (7,20 m) em t = 12 s. A força
constante aplicada pela máquina ao pacote é = (2,00 N) + (4,00 N) + (6,00 N) . Para esse
deslocamento, determine (a) o trabalho realizado pela força da máquina sobre o pacote e (b) a potência
média desenvolvida pela força.
47. (a) Equation 7-8 yields
W = Fx Δx + Fy Δy + Fz Δz
= (2.00 N)(7.5 m – 0.50 m) + (4.00 N)(12.0 m – 0.75 m) + (6.00 N)(7.2m – 0.20 m)
=101 J ≈ 1.0× 102
J.
(b) Dividing this result by 12 s (see Eq. 7-42) yields P = 8.4 W.