Carregado porManuela Mendes
www.TutoresReforcoEscolar.Com.Br - Física - Movimento Circular
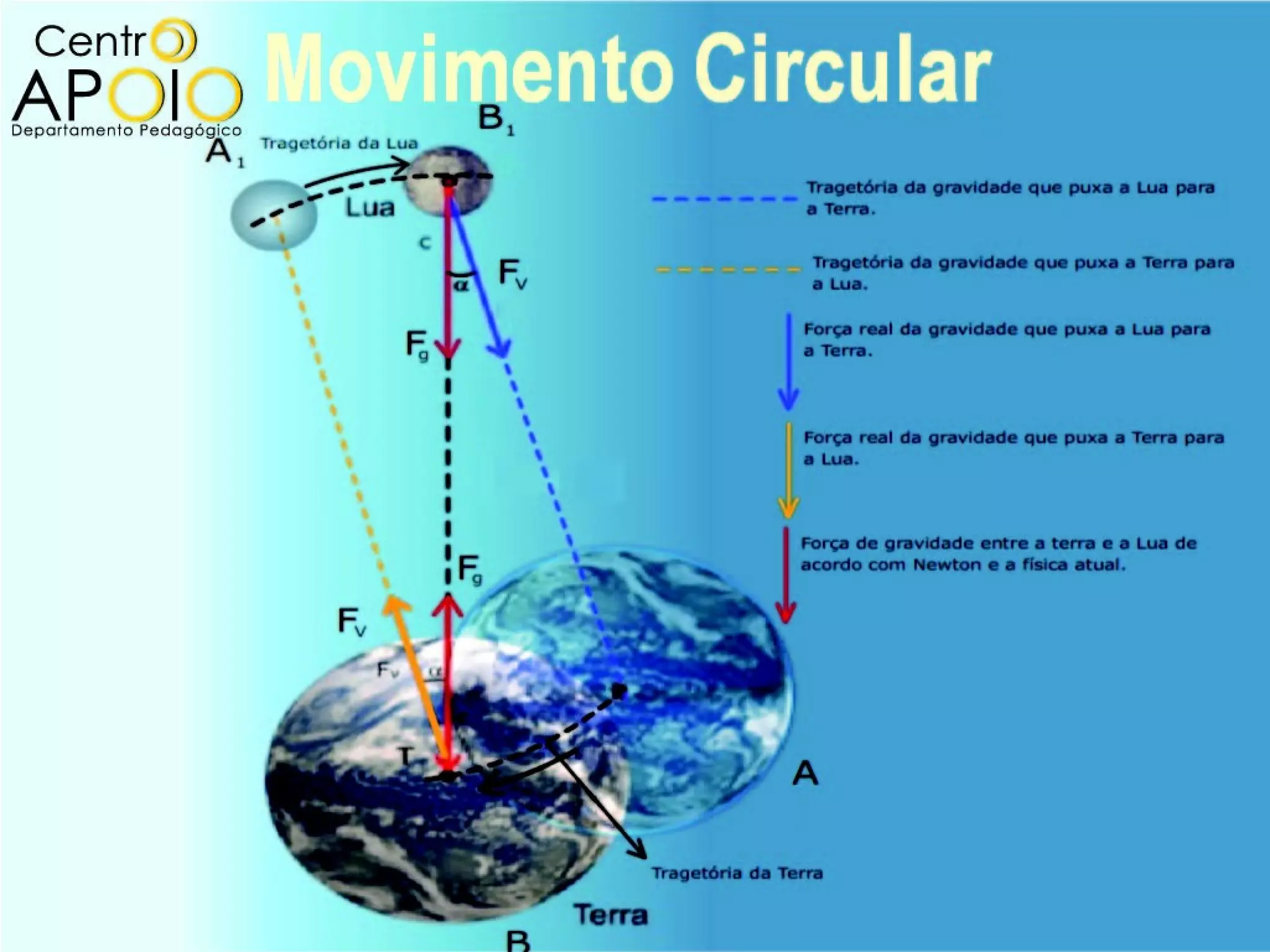
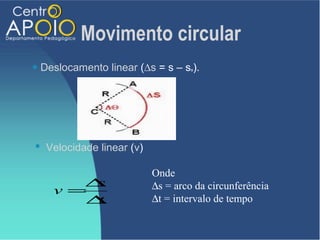
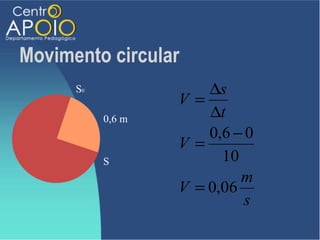
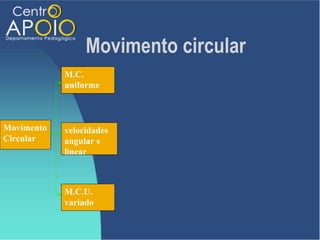
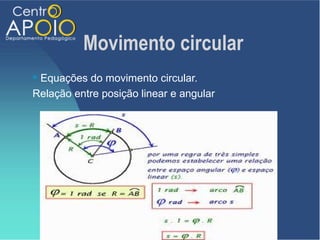
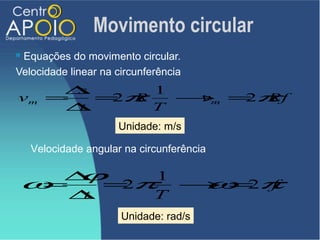
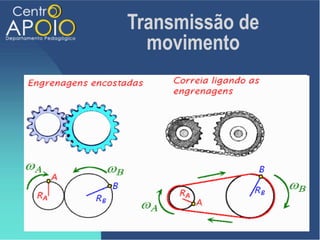
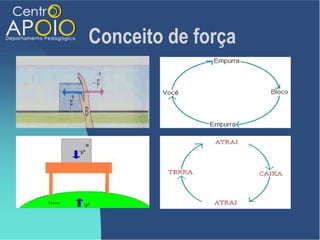
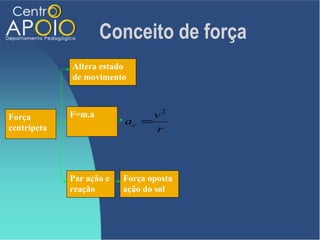
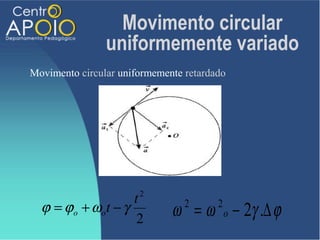
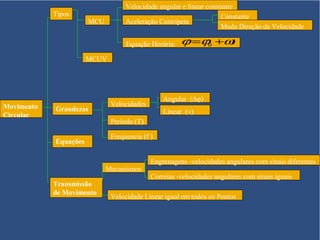
O documento discute o movimento circular, incluindo conceitos como movimento circular uniforme (mcu) e movimento circular uniformemente variado (mcuv). Ele explica definições de deslocamento angular, velocidade angular, e contém exercícios práticos para calcular a velocidade angular e linear. Além disso, aborda a aceleração centrípeta e as leis de Newton em relação ao movimento circular.
Mais conteúdo relacionado
Semelhante a www.TutoresReforcoEscolar.Com.Br - Física - Movimento Circular
www.TutoresReforcoEscolar.Com.Br - Física - Movimento Circular
- 2. Movimento Circular Se definemovimento circular como aquele cuja trajetória é uma circunferência. Eles são classificados como: • Movimento circular uniforme (MCU) •Movimento circular uniformemente variado (MCUV)
- 3. Movimento Circular M.C. uniforme Movimento Circular M.C.U. variado
- 4. Movimento circular Para entendero movimento circular, precisaremos conhecer alguns conceitos importantes : Deslocamento angular ( ∆ϕ = ϕ-ϕ ) o
- 5. Movimento Circular Velocidade angular (ω)
- 6. Movimento circular Exercício Umaroda gigante, está na posição ϕo= 0º ela faz uma rotação e para na posição ϕ=360º, num intervalo de 30 s. Qual é a sua velocidade angular média?
- 7. Movimento circular Exercício Umaroda gigante, está na posição ϕo= 0º ela faz uma rotação e para na posição ϕ = 360º, num intervalo de 30 s. Qual é a sua velocidade angular média ?
- 8. Movimento circular ω ∆ = ϕ Em radianos ∆t π__________180º Xrad________30º 360º −0º ω= 30 30π π rad xrad = = 180º 6 s 30º ω= s
- 9. Movimento circular Deslocamento linear (∆s = s – sº). Velocidade linear (v) Onde ∆s ∆s = arco da circunferência v = ∆t ∆t = intervalo de tempo
- 10. Movimento circular Exercício Umponto P num disco está em sua posição So = 0 m, após 10 s, ele percorre um arco de circunferência ficando na posição S = 0,6 m. Calcule sua velocidade linear média nesta trajetória.
- 11. Movimento circular Exercício Umponto P num disco está em sua posição So = 0 m, após 10 s, ele percorre um arco de circunferência ficando na posição S = 0,6 m. Calcule sua velocidade linear média nesta trajetória.
- 12. Movimento circular S0 ∆s V= 0,6 m ∆t 0,6 − 0 V= S 10 m V = 0,06 s
- 13. Movimento circular M.C. uniforme Movimento velocidades Circular angular e linear M.C.U. variado
- 14. Movimento circular Período(T) É o tempo gasto para dar uma volta numa circunferência. Frequência (f) É o número de voltas (n)dado pela circunferência por unidade de tempo (∆t). Onde n 1 n = número de voltas f = = ∆t = intervalo de tempo ∆ t T Quando n=1 , ∆t =T
- 15. Movimento circular Exercício Uma pessoa está em uma roda-gigante que tem raio de e gira em rotação uniforme. A pessoa passa pelo ponto mais próximo do chão a cada 20 segundos. Podemos afirmar que a frequência do movimento dessa pessoa, em rpm, (rotações por minuto) é:
- 16. Movimento circular Exercício Umapessoa está em uma roda-gigante que gira em rotação uniforme. A pessoa passa pelo ponto mais próximo do chão a cada 20 segundos. Podemos afirmar que a frequência do movimento dessa pessoa, em rpm, (rotações por minuto) é:
- 17. Movimento circular 1volta f = 20 x = 60.1 20 s 1__________20 s 60 x= = 3 rpm x__________60s 20 Ou pela aplicação da formula de frequência 1 n = 20 60 n =3rpm
- 18. Movimento circular M.C. uniforme Movimento velocidades Período e Circular angular e frequência linear M.C.U. variado
- 19. Movimento circular Definição de radiano: Um radiano é a medida do ângulo central φ que determina, na circunferência, um arco de comprimento igual ao raio R (s=R)
- 20. Movimento circular Equações domovimento circular. Relação entre posição linear e angular
- 21. Movimento circular Equaçõesdo movimento circular. Relação entre velocidade angular e linear. Dividindo os dois membros da equação anterior pelo tempo fica: ∆ s ∆ϕ = .R ∆ t ∆t ω v m = .R
- 22. Movimento circular Exercícios Nafigura, 1, 2 e 3 são partículas de massa m. A partícula 1 está presa ao ponto O pelo fio a. As partículas 2 e 3 estão presas, respectivamente, à partícula 1 e à partícula 2, pelos fios b e c. Todos os fios são inextensíveis e de massa desprezível. Cada partícula realiza um movimento com velocidade constante e centro em O. Classifique as velocidades angulares e lineares nos três pontos quanto ao seus módulos (maior, menor, ou igual).
- 23. Movimento circular Na figura,1, 2 e 3 são partículas de massa m. A partícula 1 está presa ao ponto O pelo fio a. As partículas 2 e 3 estão presas, respectivamente, à partícula 1 e à partícula 2, pelos fios b e c. Todos os fios são inextensíveis e de massa desprezível. Cada partícula realiza um movimento com velocidade constante e centro em O. Classifique as velocidades angulares e lineares nos três pontos quanto ao seus módulos (maior, menor, ou igual).
- 24. Movimento circular Comoas velocidades angulares são iguais para todos os pontos 1 2 3 0 a b c sobre a linha ω1 = ω2 = ω3 Da relação entre velocidade angular e linear vem : V=ω.R R3 > R2 > R1 V3 > V2 > V1
- 25. Movimento circular Equações domovimento circular. Velocidade linear na circunferência ∆s 1 vm = =π 2 R → =π vm 2 Rf ∆t T Unidade: m/s Velocidade angular na circunferência ω= ∆ϕ= π1 → = π 2 ω 2 f ∆t T Unidade: rad/s
- 26. Transmissão de movimento 26
- 27. Transmissão de movimento A velocidade linear nas engrenagens é a mesma em todos os pontos A velocidade linear na correia é a mesma em todos os pontos.
- 28. Transmissão de movimento Umacinta funciona solidária com dois cilindros de raios RA=10cm e RB=50cm. Supondo que o cilindro maior tenha uma frequência de rotação f B igual a 60rpm: a) Qual a frequência de rotação fA do cilindro menor? b) Qual a velocidade linear da cinta ?
- 29. Transmissão de movimento Umacinta funciona solidária com dois cilindros de raios RA=10cm e RB=50cm. Supondo que o cilindro maior tenha uma frequência de rotação fB igual a 50rpm: a) Qual a frequência de rotação fA do cilindro menor? b) Qual a velocidade linear da cinta ?
- 30. Transmissão de movimento a)f A .R A = f B .RB b) VA = 2πf A f A .10 =60.50 VA = 6,28.10.300 60.50 fA = cm 10 VA = 18800 fA =300rpm s
- 31. Movimento circular M.C. uniforme Movimento velocidades Período e Transmissão Circular angular e frequência de movimento linear M.C.U. variado
- 32. Movimento circular uniforme Alémde ter as características do movimento circular o M.C.U. possui: A velocidade de sua trajetória constante Aceleração centrípeta
- 33. Movimento circular uniforme Aaceleração centrípeta existe por que a velocidade linear muda constantemente de direção, apesar de seu módulo ser constante.
- 34. Movimento circular uniforme Exemplos de movimento circular uniforme
- 35. Movimento circular uniforme Equação horária do M.C.U. ω cte = ϕ ϕ+ t = o ω Onde ω = velocidade angular constante ϕ = posição angular
- 36. Movimento circular uniforme M.C. Modulo veloc. Aceleração uniforme Linear cte centrípeta cte Movimento velocidades Período e Transmissão Circular angular e frequência de movimento linear M.C.U. variado
- 37. Conceito de força 1a Lei de Newton: Inércia “Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças aplicadas sobre ele”.
- 38. Conceito de força 1a Lei de Newton: Inércia “Todo corpo continua em seu estado de repouso ou de movimento uniforme em uma linha reta, a menos que seja forçado a mudar aquele estado por forças aplicadas sobre ele”.
- 39. Conceito de força Altera estado de movimento Força centrípeta
- 40. Conceito de força Omenino tende a manter o estado anterior de movimento, mesmo depois do cavalo frear. Como estão soltos, o menino acaba sendo arremessado.
- 41. Conceito de força 2a Lei de Newton: F = m.a “A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção de linha reta na qual aquela força é imprimida.”
- 42. Conceito de força 2a Lei de Newton: F = m.a “A mudança de movimento é proporcional à força motora imprimida, e é produzida na direção de linha reta na qual aquela força é imprimida.”
- 43. Conceito de força Nocaso abaixo as forças aplicadas estão na mesma direção e sentido e tem mesmo módulo, essas forças produzem acelerações diretamente proporcionais na sua mesma direção e sentido.
- 44. Conceito de força Altera estado de movimento Força centrípeta F= m.a
- 45. Conceito de força 3a Lei de Newton: pares de ação e reação “A toda ação há sempre uma reação oposta e de igual intensidade, ou, as ações mútuas de 2 corpos um sobre o outro são sempre iguais e dirigidas a partes opostas"
- 46. Conceito de força 3a Lei de Newton: pares de ação e reação “A toda ação há sempre uma reação oposta e de igual intensidade, ou, as ações mútuas de 2 corpos um sobre o outro são sempre iguais e dirigidas a partes opostas"
- 47. Conceito de força Altera estado de movimento Força F=m.a centrípeta Par de ação e reação
- 48. Conceito de força 3aLei de Newton: pares de ação e reação são : Forças simultâneas Que podem ser : Forças de campo ou de contato
- 49.
- 50. Conceito de força Altera estado de movimento Força F=m.a centrípeta Par ação e Força oposta reação ação do sol
- 51. Aceleração centrípeta Força no sol muda direção da velocidade dos planetas, através da aceleração centrípeta Em intervalos muito pequenos de tempo, podemos aproximar um arco de circunferência para triângulos semelhantes θ=v.∆t = ∆ v r v ∆ v v2 θ= = = a ∆t r
- 52. Conceito de força Altera estado de movimento Força F=m.a v2 ac = centrípeta r Par ação e Força oposta reação ação do sol
- 53.
- 54. Força centrípeta Altera estado Muda direção de movimento da trajetória Força v2 F=m.a ac = centrípeta r Par ação e Força oposta reação ação do sol
- 55. Força centrípeta As 3 leis de Newton e a força centrípeta : O sol atrai a terra e a terra atrai o sol, como o sol tem maior massa, a terra que é puxada, não cai no sol por que gira, mudando de direção a cada momento provocando uma força que equilibra, essa é a força centrípeta.
- 56. Força centrípeta Altera estado Muda direção Primeira Lei de de movimento da trajetória Newton Força F=m.a v2 Segunda Lei ac = de Newton centrípeta r Par ação e Força oposta Terceira lei reação ação do sol de Newton
- 57. Força centrípeta Aplicando aaceleração centrípeta na segunda lei de Newton : 2 v F =m. r
- 58. Estrutura da apresentação Altera estado Muda direção Primeira Lei de de movimento da trajetória Newton Força F=m.a v2 Segunda Lei v2 ac = de Newton F =m. centrípeta r r Par ação e Força oposta Terceira lei reação ação do sol de Newton
- 59. Exercícios Um carro demassa 1,0 x 103 kg com velocidade de 20 m/s descreve no plano horizontal uma curva de raio 200 m. A força centrípeta e o coeficiente de atrito tem módulos:
- 60. Exercícios Um carro demassa 1,0 x 103 kg com velocidade de 20 m/s descreve no plano horizontal uma curva de raio 200 m. A força centrípeta e o coeficiente de atrito tem módulos:
- 61. Força centrípeta A) Fc= m.v2/ R Fc= 1,0 x 103 . (20)2 / 200 Fc= 2000 N B) Fat = Fc Fat = µN = µmg 2000 = µmg 2000 = µ.1000. 10
- 62. Movimento circular uniformemente variado Características: Possui aceleração tangencial constante (γ) A velocidade em sua trajetória varia de forma uniforme. ω 0 ω ≠ω 0 ω
- 63. Movimento circular uniformemente variado M.C. Modulo veloc. Aceleração Aceleração uniforme Linear cte ≠ 0 centrípeta tangencial cte ≠ 0 cte = 0 Movimento velocidades Período e Transmissão Circular angular e frequência de movimento linear M.C.U. Aceleração variado tangencial cte ≠ 0
- 64. Movimento circular uniformemente variado Movimento circular uniformemente retardado 2 t ϕ = ϕ o + ωo t − γ 2 ω = ω o − 2γ .∆ ϕ 2 2
- 65. Movimento circular uniformemente variado Movimento circular uniformemente acelerado 2 t ϕ = ϕ o + ωot + γ ω = ω o + 2γ .∆ ϕ 2 2 2
- 66. Movimento circular uniformemente variado Módulo da aceleração resultante no M.C.U.V. aceleração centrípeta v2 ac = R aceleração tangencial ∆ω at = γ = ∆t
- 67. Movimento circular uniformemente variado Módulo da aceleração resultante no M.C.U.V. Onde ar = aceleração resultante a r=a c+a 2 2 2 t
- 68. Movimento circular uniformemente variado M.C. Modulo veloc. Aceleração Aceleração uniforme Linear cte ≠ 0 centrípeta tangencial = 0 cte ≠ 0 Movimento velocidades Período e Transmissão Circular angular e frequência de movimento linear M.C.U. Aceleração Aceleração variado tangencial cte ≠ 0 centrípeta varia
- 69. Velocidade angular elinear constante Tipos Constante MCU Aceleração Centrípeta Muda Direção da Velocidade Equação Horária: ϕ =ϕ0 +ωt Características Aceleração Tngencial constante e diferente de zero MCUV Aceleração Centrípeta varia Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial t2 Grandezas Equações ϕ =ϕ +ω t +γ 0 0 2 Movimento Retardado ω =ω +2γ ϕ 2 2 0 ∆ Velocidade Circular s Velocidade tangencial mesmo sentido da velocidade tangencial t2 Equações ϕ= 0 + 0t =γ ϕ ω 2 ω= 0 −γ ϕ 2 ω 2 ∆ 2 Equações Força Centrípeta Trasmisão de Movimento
- 70. Tipos MCU MCUV Movimento Circular
- 71. Tipos MCU MCUV Angular (Δφ) Movimento Velocidades Grandezas Linear (v) Circular
- 72. Tipos MCU MCUV Angular (Δφ) Movimento Velocidades Grandezas Linear (v) Circular Período (T) Frequencia (f )
- 73. Tipos MCU MCUV Angular (Δφ) Velocidades Grandezas Linear (v) Período (T) Frequencia (f ) Movimento s =ϕ⋅ R Circular vm =ω⋅ R Equações 1 vm =2πR =2πRf t 1 ω=2π =2πRf t Engrenagens -velocidades angulares com sinais diferentes Mecanismos Correias -velocidades angulares com sinais iguais Transmissão de Movimento Velocidade Linear igual em todos os Pontos
- 74. Velocidade angular elinear constante Tipos Constante MCU Aceleração Centrípeta Muda Direção da Velocidade Equação Horária: ϕ =ϕ0 +ωt MCUV Angular (Δφ) Movimento Velocidades Grandezas Linear (v) Circular Período (T) Frequencia (f ) Equações Engrenagens -velocidades angulares com sinais diferentes Mecanismos Correias -velocidades angulares com sinais iguais Transmissão de Movimento Velocidade Linear igual em todos os Pontos
- 75. Velocidade angular elinear constante Tipos Constante MCU Aceleração Centrípeta Muda Direção da Velocidade Equação Horária: ϕ =ϕ0 +ωt MCUV Angular (Δφ) Velocidades Grandezas Linear (v) Período (T) Movimento Equações Frequencia (f ) Circular Engrenagens -velocidades angulares com sinais diferentes Mecanismos Correias -velocidades angulares com sinais iguais Transmissão de Movimento Velocidade Linear igual em todos os Pontos Depende das Leis de Newton Altera o estado de movimento Fórmula: mv 2 Fc = Força R Centrípeta Gera Aceleração Centrípeta – Formula: v2 ac = R
- 76. Velocidade angular elinear constante Tipos Constante MCU Aceleração Centrípeta Muda Direção da Velocidade Equação Horária: ϕ =ϕ0 +ωt Características Aceleração Tngencial constante e diferente de zero MCUV Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial t2 Equações ϕ =ϕ +ω t +γ 0 0 2 Grandezas Movimento Retardado ω =ω +2γ ϕ 2 2 0 ∆ Circular Velocidade tangencial mesmo sentido da velocidade tangencial Equações Equações t2 ϕ= 0 + 0t =γ ϕ ω 2 ω= 0 −γ ϕ 2 ω 2 ∆ 2 Transmissão de Movimento Força Centrípeta
- 77. Velocidade angular elinear constante Tipos Constante MCU Aceleração Centrípeta Muda Direção da Velocidade Equação Horária: ϕ =ϕ0 +ωt Características Aceleração Tngencial constante e diferente de zero MCUV Aceleração Centrípeta varia Tipos Acelerado Velocidade tangencial mesmo sentido da velocidade tangencial t2 Equações ϕ =ϕ +ω t +γ 0 0 2 Grandezas Movimento Retardado ω =ω +2γ ϕ 2 2 0 ∆ Circular Velocidade tangencial mesmo sentido da velocidade tangencial Equações Equações t2 ϕ= 0 + 0t =γ ϕ ω 2 ω= 0 −γ ϕ 2 ω 2 ∆ 2 Transmissão de Movimento Força Centrípeta
- 78. Lembrando a Geometria 2π rad = 360º Comprimento da Circunferência C= π 2 R
- 79. Conceito de Força •1ªLei de Newton: Inércia •2ª Lei de Newton: F = m.a •3ª Lei de Newton: Ação e Reação