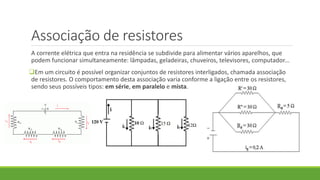
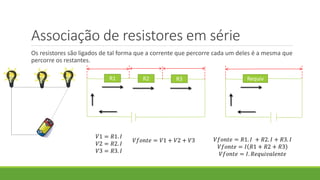
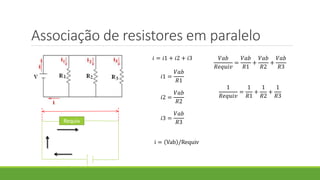
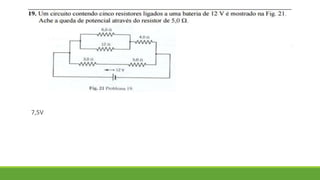
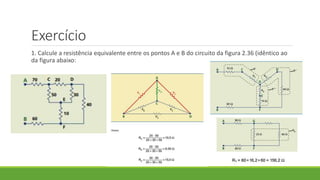
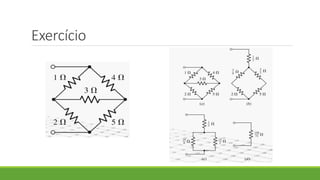
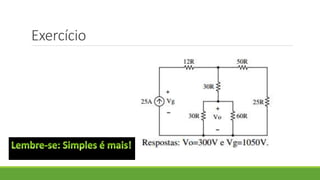
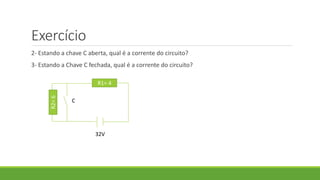
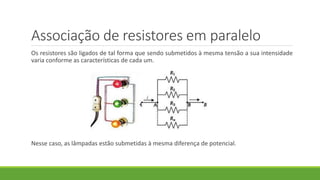
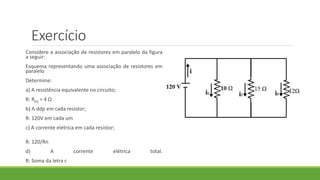
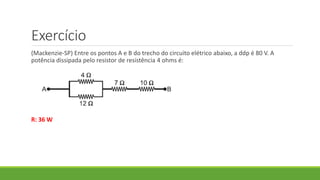
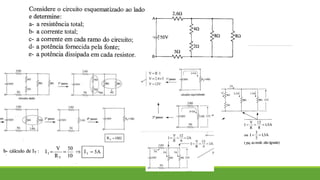
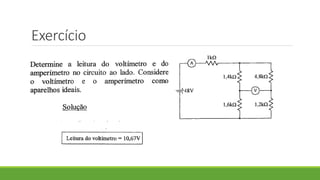
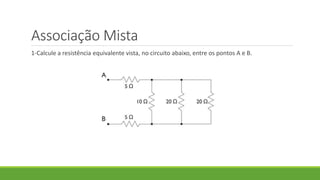
1. O documento discute os conceitos de associação de resistores em série, paralelo e mista, incluindo cálculos de resistência equivalente e corrente. 2. É apresentado um exemplo de exercício resolvido sobre associação de resistores em paralelo. 3. As transformações delta-estrela e estrela-delta são introduzidas como métodos para resolver circuitos mistos complexos.

1. Eletroeletrônica
Aplicada
GIGLLIARA SEGANTINI DE MENEZES
E N G E N H E I R A D E P R O D U Ç Ã O – U F E S
T É C N I C A E M E L E T R O T É C N I C A – I F E S
INSTITUTO FEDERAL
ESPÍRITO SANTO Agosto de 2016

2. Relatório 2 – 3 pessoas
Tema:
1. Curto-circuito, Fusíveis e disjuntores
 Tipos
 Características
 Funcionamento
 Aplicações
 Sortear quem vai apresentar
 Valor: 5 pontos
 A nota do grupo será a nota da pessoa que apresentou

3. Associação de resistores
A corrente elétrica que entra na residência se subdivide para alimentar vários aparelhos, que
podem funcionar simultaneamente: lâmpadas, geladeiras, chuveiros, televisores, computador...
Em um circuito é possível organizar conjuntos de resistores interligados, chamada associação
de resistores. O comportamento desta associação varia conforme a ligação entre os resistores,
sendo seus possíveis tipos: em série, em paralelo e mista.

4. Associação de resistores em série
Os resistores são ligados de tal forma que a corrente que percorre cada um deles é a mesma que
percorre os restantes.
R1 R2 R3
𝑉1 = 𝑅1. 𝐼
𝑉2 = 𝑅2. 𝐼
𝑉3 = 𝑅3. 𝐼
𝑉𝑓𝑜𝑛𝑡𝑒 = 𝑉1 + 𝑉2 + 𝑉3 𝑉𝑓𝑜𝑛𝑡𝑒 = 𝑅1. 𝐼 + 𝑅2. 𝐼 + 𝑅3. 𝐼
𝑉𝑓𝑜𝑛𝑡𝑒 = 𝐼 𝑅1 + 𝑅2 + 𝑅3
𝑉𝑓𝑜𝑛𝑡𝑒 = 𝐼. 𝑅𝑒𝑞𝑢𝑖𝑣𝑎𝑙𝑒𝑛𝑡𝑒
Requiv

5. Associação de resistores em série

7. Exercício
Considerando-se o circuito elétrico da figura (a) abaixo. É correto afirmar que o gráfico da figura
(b) representa corretamente as variações no potencial elétrico em cada parte do circuito
equivalente.

8. Exercício
2- Estando a chave C aberta, qual é a corrente do circuito?
3- Estando a Chave C fechada, qual é a corrente do circuito?
R1= 4
R2=6
32V
C

9. Associação de resistores em paralelo
Os resistores são ligados de tal forma que sendo submetidos à mesma tensão a sua intensidade
varia conforme as características de cada um.
Nesse caso, as lâmpadas estão submetidas à mesma diferença de potencial.

10. Associação de resistores em paralelo
𝑖 = 𝑖1 + 𝑖2 + 𝑖3
𝑖1 =
𝑉𝑎𝑏
𝑅1
𝑖2 =
𝑉𝑎𝑏
𝑅2
𝑖3 =
𝑉𝑎𝑏
𝑅3Requiv
i = Vab /Requiv
𝑉𝑎𝑏
𝑅𝑒𝑞𝑢𝑖𝑣
=
𝑉𝑎𝑏
𝑅1
+
𝑉𝑎𝑏
𝑅2
+
𝑉𝑎𝑏
𝑅3
1
𝑅𝑒𝑞𝑢𝑖𝑣
=
1
𝑅1
+
1
𝑅2
+
1
𝑅3

11. Exercício
Considere a associação de resistores em paralelo da figura
a seguir:
Esquema representando uma associação de resistores em
paralelo
Determine:
a) A resistência equivalente no circuito;
R: Req = 4 Ω
b) A ddp em cada resistor;
R: 120V em cada um
c) A corrente elétrica em cada resistor;
R: 120/Rn
d) A corrente elétrica total.
R: Soma da letra c

13. Associação de 2 resistores em paralelo
Atalho para o cálculo da resistência equivalente em associações em paralelo:
Associação de n resistores iguais em paralelo
Associação de 2 resistores diferentes em paralelo
Duas regrinhas interessantes para lembrar,
que ajudam a verificar o resultado obtido.
Numa associação em série, a resistência
equivalente é maior do que a maior
resistência presente no circuito.
Numa associação em paralelo, a resistência
equivalente é menor do que a menor
resistência presente no circuito.

14. Vantagens da associação em paralelo

15. Exercício
(UECE 88.2) A figura representa um circuito elétrico com duas lâmpadas L1 e L2, iguais e ligadas
em paralelo. A resistência de cada lâmpada é de 10 ohms, a diferença de potencial entre os
pontos A e B vale 3 volts e o fusível F suporta uma corrente máxima de 0,8 ampères. Colocando-
se uma terceira lâmpada, igual às anteriores, em paralelo com as demais:
a) haverá alteração na d.d.p. entre A e B.
b) passará mais correntes nas lâmpadas L1 e L2.
c) a resistência equivalente das lâmpadas aumentará.
d) o fusível queimará.

16. Pedro!
(UECE 86.1) Na figura abaixo, o potencial do ponto B é igual ao potencial do ponto D. A
intensidade de corrente que entra no circuito através do ponto A é i = 3 A. A resistência R1 = 40
Ω, R2 = 10 Ω e R3 = 5 Ω. Nestas condições, a potência dissipada na resistência R4, vale:
a) 40 W b) 180 W c) 20 W d) 80 W
I. Como VA = VB, então: R1.R3 = R2.R4 → 40.5 = 10.R4 → R4 = 20 Ω.
II. U1 = U2 → 50.i1 = 25.i2 → i2 = 2.i1, logo i2 = 2 A e i1 = 1 A.
III. P4 = R4.i2
2 = 20.22 = 20.4 = 80 W.

17. Associação Mista
1-Calcule a resistência equivalente vista, no circuito abaixo, entre os pontos A e B.

18. 7,5V

19. Exercício
(ITA-SP) Determine a intensidade da corrente que atravessa o resistor R2 da figura quando a
tensão entre os pontos A e B for igual a V e as resistências R1; R2 e R3 forem iguais a R
a) V/R b) V/3R c) 3V/R d) 2V/3R
e) nenhuma das anteriores

20. Exercício
(Mackenzie-SP) Entre os pontos A e B do trecho do circuito elétrico abaixo, a ddp é 80 V. A
potência dissipada pelo resistor de resistência 4 ohms é:
R: 36 W

23. Exercício

24. Circuitos elétricos especiais
1. Redesenhando o circuito
1. Requivalente?
2. R1=12Ω
3. R2= 6Ω
4. R3= 2Ω
A C B R: 6

25. Exercício
19V

26. Transformações delta-estrela (DY) ou
estrela-delta (YD)
As técnicas estudadas até agora permitem resolver a grande maioria dos casos de associação de
resistores. Existem algumas situações, porém, em que a determinação da resistência
equivalente não é possível com os recursos conhecidos. É o caso do circuito misto da figura
abaixo. Sugere-se que o leitor tente calcular a resistência equivalente entre os pontos A e B, a
fim de compreender a dificuldade da situação.
Nesse circuito, não é possível encontrar nenhum par de resistores associados em série nem em
paralelo. Tais casos podem ser resolvidos utilizando as transformações delta-estrela (DY) ou
estrela-delta (YD).

27. Transformação (DY)
São conhecidas as resistências do triângulo (delta)
formado pelos resistores R1, R2, R3, com vértices nos
nós A, B e C, indicados na figura “a”.
Na ligação equivalente em estrela, surge um quarto
ponto (D, central). Cada resistência na estrela é a
ligação desse ponto com o vértice respectivo no
triângulo.
Serão determinadas as resistências da estrela
equivalente, formada pelos resistores RA, RB, RC,
mostrados na figura “b”.

28. Transformações

29. Exercício
1. Calcule a resistência equivalente entre os pontos A e B do circuito da figura 2.36 (idêntico ao
da figura abaixo:

30. Exercício

31. Exercício

32. Ponte de Wheatstone

34. Referências
Básica
ANTONIO PERTENCE JR. Eletrônica analógica: amplificadores operacionais e filtros ativos - 6ª
edição
Complementar
MIKE TOOLEY. Circuitos Eletrônicos: Fundamentos e Aplicações. Elsevier, São Paulo 2006.
MARCELO WENDLING. Amplificadores Operacionais. Disponível em<
netsoft.inf.br/aulas/4_EAC_Eletronica_Basica/3__Amplificador_Operacional.pdf>