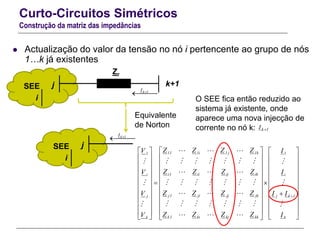
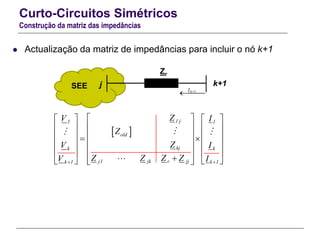
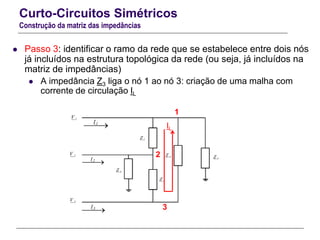
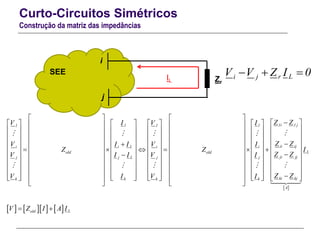
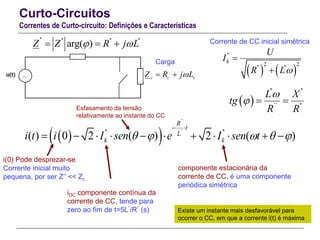
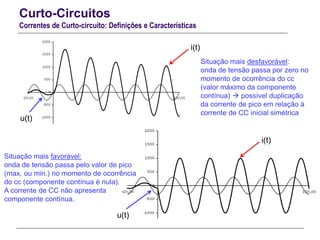
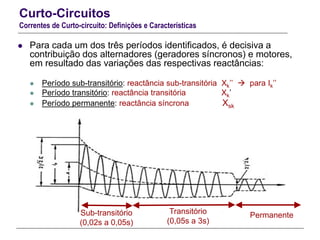
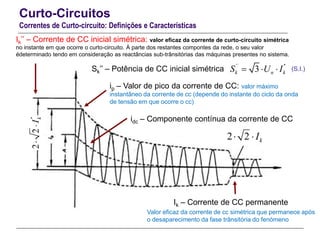
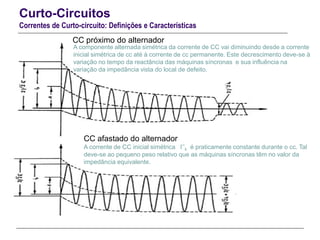
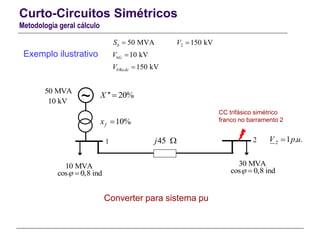
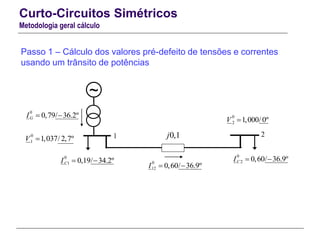
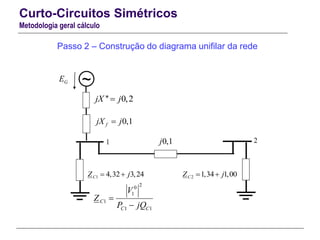
O documento resume conceitos gerais sobre curto-circuitos em sistemas elétricos de energia, incluindo suas causas, consequências e tipos. Explica como os curto-circuitos afetam a corrente e tensão no sistema, e como seus efeitos devem ser considerados no dimensionamento de equipamentos. Também define termos relacionados às correntes de curto-circuito e descreve os modelos usados para analisar curto-circuitos simétricos.





















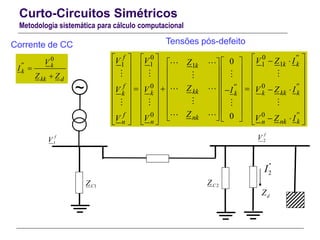
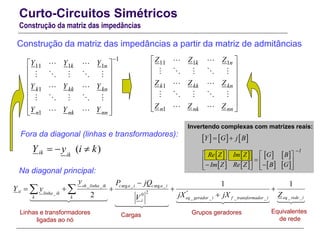
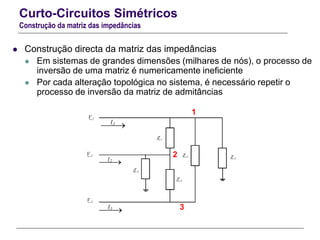
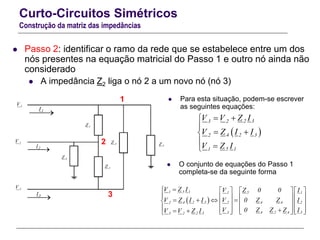
![Curto-Circuitos Simétricos
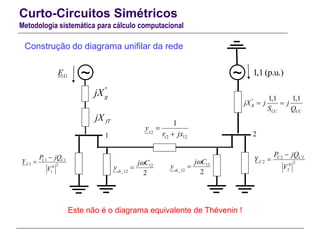
Metodologia sistemática para cálculo computacional
1 1
1 20
1
C C
C
P jQ
Y
V
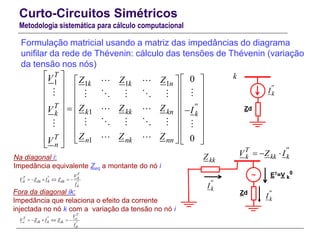
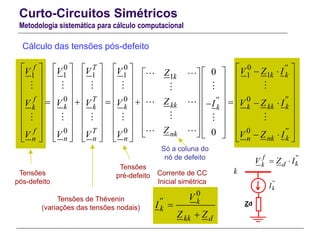
Diagrama unifilar equivalente de Thévenin
Construção da matriz [Y] equivalente de Thévenin
''
gjX
fTjX
''
RjX
j B j
12 12
1
_122'' 2 20
1
1 C
sh
g fT
Q x
y
X X r xV
12
_12
2sh
j C
y
12
_12
2sh
j C
y
12 12
2
2'' 2 2_120
2
1 C
sh
R
Q x
y
X r xV
12 12
2 2
x
r x
12 12
2 2
x
r x
Y G j B
2 2 2 212
12 12 12 12
r x
y j
r x r jx
2 2
2 20
2
C C
C
P jQ
Y
V
](https://image.slidesharecdn.com/17-curtocircuitoconceitosgerais-190927181654/85/17-curto-circuito-conceitos-gerais-35-320.jpg)
![Curto-Circuitos Simétricos
Metodologia sistemática para cálculo computacional
Diagrama unifilar equivalente de Thévenin
''
gjX
fTjX
''
RjX
G
12 12
1 12
2 2 20
1
CP r
r xV
12
_12
2sh
j C
y
12
_12
2sh
j C
y
12 12
2
2 2 20
1
CP r
r xV
12 12
2 2
r
r x
12 12
2 2
r
r x
Y G j B
Geralmente é possível
desprezar [G]
(erros inferiores a 1%)
1 1
1 20
1
C C
C
P jQ
Y
V
2 2 2 212
12 12 12 12
r x
y j
r x r jx
2 2
2 20
2
C C
C
P jQ
Y
V
](https://image.slidesharecdn.com/17-curtocircuitoconceitosgerais-190927181654/85/17-curto-circuito-conceitos-gerais-36-320.jpg)
![Curto-Circuitos Simétricos
Metodologia sistemática para cálculo computacional
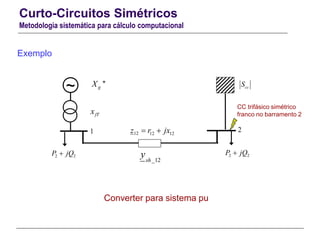
Pode ser obtida por inversão de [Y], trabalhando com complexos.
Ou mais fácil: invertendo matrizes reais:
Pode ser obtida por construção directa adicionando sistematicamente os nós e
ramos da rede
Inversão da matriz [Y] para obter a matriz [Z]
1
G B
B G
Re Im
Im Re
Z Z
Z Z
Y G j B ](https://image.slidesharecdn.com/17-curtocircuitoconceitosgerais-190927181654/85/17-curto-circuito-conceitos-gerais-37-320.jpg)