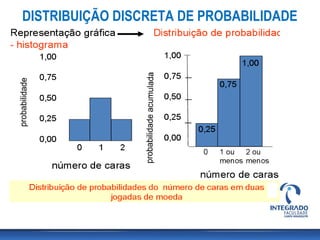
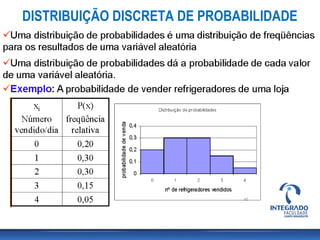
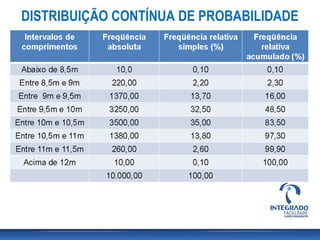
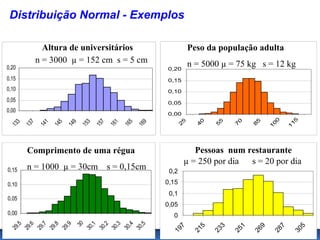
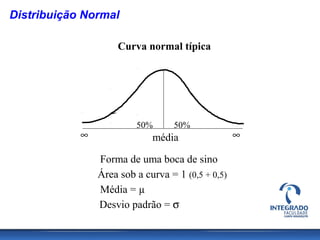
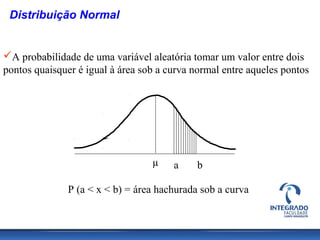
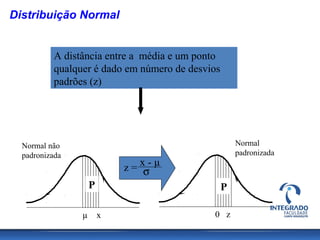
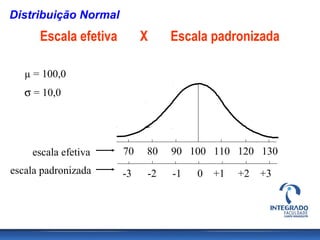
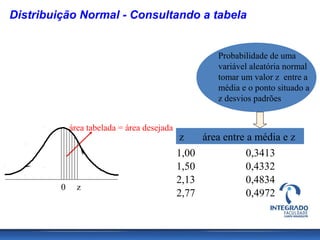
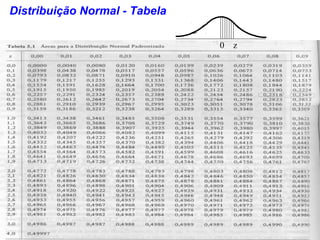
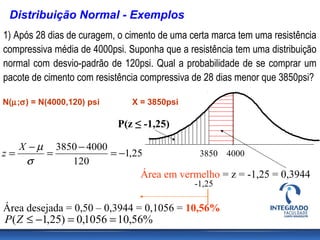
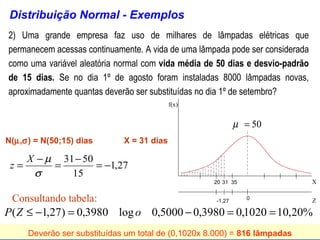
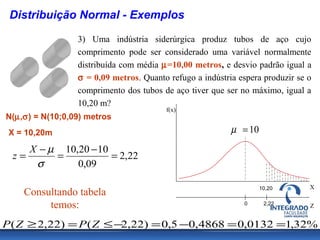
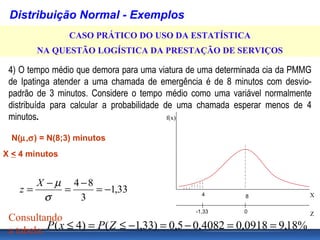
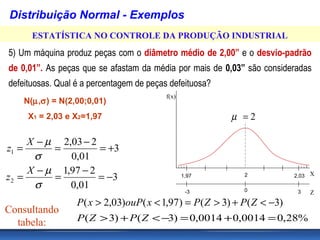
O documento aborda conceitos de probabilidade e distribuições estatísticas, destacando distribuições discretas e contínuas, como a normal. A distribuição normal é explicada em termos de suas características e importância, incluindo exemplos práticos e cálculos de probabilidade relacionados a variáveis normalmente distribuídas. Inclui também casos de aplicação da estatística na análise de dados e controle de produção.

1. AULA 25
ESTATÍSTICA
Professor: João Alessandro
PROBABILIDADE
PARTE 2

2. PROBABILIDADE

3. PROBABILIDADE

4. PROBABILIDADE

5. PROBABILIDADE

7. DISTRIBUIÇÃO DISCRETA DE PROBABILIDADE

8. DISTRIBUIÇÃO DISCRETA DE PROBABILIDADE

9. DISTRIBUIÇÃO CONTÍNUA DE PROBABILIDADE

10. DISTRIBUIÇÃO CONTÍNUA DE PROBABILIDADE

11. Distribuição de Probabilidades
A distribuição de probabilidades indica a percentagem de
vezes que, em grande quantidade de observações,
podemos esperar a ocorrência de vários resultados de uma
variável aleatória.
Em uma distribuição de probabilidades é necessário:
∑ P(x) = 1, onde x toma todos valores possíveis
0 ≤ P(x) ≤ 1 para todo o x.
Distribuições
descontínuas ou
Distribuições de discretas
probabilidade
Distribuições
contínuas

12. Distribuições Descontínuas ou Discretas
Envolvem distribuições de probabilidades de variáveis aleatórias
relativas a dados que podem ser contados.
Exemplos:
 Número de ocorrências por amostras
 Número de ocorrências por unidade num intervalo de tempo
 Número de fumantes presentes em eventos esportivos
Uniforme ou Retangular
Binomial
Formas da Binomial Negativa ou de Pascal
distribuição Geométrica
descontínua Poisson
Multinomial ou Polinomial
Hipergeométrica

13. Distribuições Contínuas
Quando se usa as distribuições contínuas?
 A variável aleatória discreta apresenta um grande número de resultados;
A variável aleatória em questão é contínua.
Os ponteiros de um relógio podem parar em qualquer dos infinitos
pontos do círculo
logo A probabilidade de parar em um ponto definido é zero
Nas distribuições contínuas utilizam-se a probabilidade da ocorrência
em um intervalo P(a < x < b);
Em uma distribuição contínua, a probabilidade é dada pela área
contida no intervalo considerado.

14. Distribuições Contínuas
UNIFORME OU RETANGULAR
NORMAL
BIVARIADA NORMAL
EXPONENCIAL
LOGNORMAL
DISTRIBUIÇÕES
WEIBULL
CONTÍNUAS
( formas) QUI-QUADRADO χ 2
t DE STUDENT
F DE SNEDECOR
GAMA
BETA
ERLANG

15. Distribuição Normal
Um pouco de história
No século XVIII, astrônomos e outros
cientistas observaram que medidas
repetidas de mensurações como a
distância à lua variavam como na figura,
quando coletadas em grande número.
Esta forma gráfica era associada aos
erros de mensuração, daí o nome de
“Distribuição normal dos erros” e depois
“Distribuição normal”
Também é conhecida por “Distribuição
Gaussiana”, em função do modelo
matemático desenvolvido por Karl F.
Gauss para este comportamento.

16. Distribuição Normal - Exemplos
Altura de universitários Peso da população adulta
n = 3000 µ = 152 cm s = 5 cm n = 5000 µ = 75 kg s = 12 kg
0,20 0,20
0,15 0,15
0,10 0,10
0,05 0,05
0,00
0,00
0
5
5
0
5
0
5
7
1
3
1
5
3
5
9
7
9
0
1
15
16
2
4
5
7
8
13
13
14
14
14
15
16
16
1
1
Comprimento de uma régua Pessoas num restaurante
µ = 250 por dia s = 20 por dia
0,15 n = 1000 µ = 30cm s = 0,15cm 0,2
0,10 0,15
0,1
0,05
0,05
0,00 0
30
,5
,6
,7
,8
,9
,1
,2
,3
,4
,5
3
1
7
5
9
7
5
29
29
29
29
29
30
30
30
30
30
19
21
23
25
26
28
30

17. Distribuição Normal
IMPORTÂNCIA DA DISTRIBUIÇÃO NORMAL
Retrata com boa aproximação, as distribuições de freqüência de
muitos fenômenos naturais e físicos.
Serve como aproximação das probabilidades binomiais (sim ou
não) quando n é grande.
Representa a distribuição das médias e proporções em grandes
amostras, o que tem relevante implicação na amostragem (a mais
importante).

18. Distribuição Normal
Curva normal típica
50% 50%
∞ média ∞
Forma de uma boca de sino
Área sob a curva = 1 (0,5 + 0,5)
Média = µ
Desvio padrão = σ

19. Distribuição Normal - Características
1. A curva normal tem a forma de sino
2. É simétrica em relação a média
3. Prolonga-se de -∞ a +∞ (apenas em teoria) (assintótica)
4. Fica completamente especificada por sua média e seu desvio padrão;
há uma distribuição normal para cada par (média e desvio padrão)
5. A área total sob a curva é considerada 100% ou igual a 1
6. A área sob a curva entre dois pontos é a probabilidade de uma
variável normalmente distribuída tomar um valor entre esses pontos
7. A probabilidade de uma variável aleatória normalmente distribuída
tomar exatamente determinado valor (pontual) é zero (característica
da distribuição contínua)
8. A área sob a curva entre a média e um ponto arbitrário é função do
número de desvios padrões entre a média e aquele ponto

20. Distribuição Normal
A probabilidade de uma variável aleatória tomar um valor entre dois
pontos quaisquer é igual à área sob a curva normal entre aqueles pontos
µ a b
P (a < x < b) = área hachurada sob a curva

21. Distribuição Normal
2
1 e
( )
-1 x - µ
2 σ
x – ponto considerado da distrib.
µ - média da distribuição
f(x) =
2π σ σ - desvio padrão da distribuição
OBSERVAÇÃO:
x - µ = distância do ponto considerado à média
z= x - µ número de desvios padrões a contar da média. Ex.: 2,5
σ desvios padrões
z = valor z ou score z. Pode-se obter valores negativos de z para
valores de x inferiores à média

22. Distribuição Normal
A distância entre a média e um ponto
qualquer é dado em número de desvios
padrões (z)
Normal não Normal
padronizada padronizada
z = xσ- µ
P P
µ x 0 z

23. Distribuição Normal
Escala efetiva X Escala padronizada
µ = 100,0
σ = 10,0
escala efetiva 70 80 90 100 110 120 130
escala padronizada -3 -2 -1 0 +1 +2 +3

24. Distribuição Normal - Consultando a tabela
1,25
.
.
.
1,0 00 01 02 03 04 05 06 ...
1,1
0,3944
olhando
1,2
. a tabela
.
.

25. Distribuição Normal - Consultando a tabela
Probabilidade de uma
variável aleatória normal
tomar um valor z entre a
média e o ponto situado a
z desvios padrões
área tabelada = área desejada
z área entre a média e z
1,00 0,3413
1,50 0,4332
2,13 0,4834
0 z
2,77 0,4972

26. Distribuição Normal - Consultando a tabela
z P(0 < x < z) P(x > z) = 0,5 – P(0 < x < z)
0 z

27. Distribuição Normal - Tabela
0 z

28. Distribuição Normal - Exemplos
1) Após 28 dias de curagem, o cimento de uma certa marca tem uma resistência
compressiva média de 4000psi. Suponha que a resistência tem uma distribuição
normal com desvio-padrão de 120psi. Qual a probabilidade de se comprar um
pacote de cimento com resistência compressiva de 28 dias menor que 3850psi?
N(µ;σ) = N(4000,120) psi X = 3850psi
P(z ≤ -1,25)
X − µ 3850 − 4000
z= = = −1,25 3850 4000
σ 120
Área em vermelho = z = -1,25 = 0,3944
-1,25
Área desejada = 0,50 – 0,3944 = 0,1056 = 10,56%
P ( Z ≤ −1,25) = 0,1056 = 10,56%

29. Distribuição Normal - Exemplos
2) Uma grande empresa faz uso de milhares de lâmpadas elétricas que
permanecem acessas continuamente. A vida de uma lâmpada pode ser considerada
como uma variável aleatória normal com vida média de 50 dias e desvio-padrão
de 15 dias. Se no dia 1º de agosto foram instaladas 8000 lâmpadas novas,
aproximadamente quantas deverão ser substituídas no dia 1º de setembro?
f(x)
µ = 50
N(µ,σ) = N(50;15) dias X = 31 dias
X − µ 31 − 50
z= = = −1,27
σ 15
20 31 35 X
Consultando tabela: -1,27 0 Z
P ( Z ≤ −1,27) = 0,3980 log o 0,5000 − 0,3980 = 0,1020 = 10,20%
Deverão ser substituídas um total de (0,1020x 8.000) = 816 lâmpadas

30. Distribuição Normal - Exemplos
3) Uma indústria siderúrgica produz tubos de aço cujo
comprimento pode ser considerado uma variável normalmente
distribuída com média µ=10,00 metros, e desvio padrão igual a
σ = 0,09 metros. Quanto refugo a indústria espera produzir se o
comprimento dos tubos de aço tiver que ser no máximo, igual a
10,20 m?
f(x)
N(µ,σ) = N(10;0,09) metros
X = 10,20m µ = 10
X − µ 10,20 − 10
z= = = 2,22
σ 0,09
10,20 X
Consultando tabela
temos: 0 2,22 Z
P ( Z ≥ 2,22) = P ( Z ≤ −2,22) = 0,5 −0,4868 = 0,0132 =1,32%

31. Distribuição Normal - Exemplos
CASO PRÁTICO DO USO DA ESTATÍSTICA
NA QUESTÃO LOGÍSTICA DA PRESTAÇÃO DE SERVIÇOS
4) O tempo médio que demora para uma viatura de uma determinada cia da PMMG
de Ipatinga atender a uma chamada de emergência é de 8 minutos com desvio-
padrão de 3 minutos. Considere o tempo médio como uma variável normalmente
distribuída para calcular a probabilidade de uma chamada esperar menos de 4
minutos. f(x)
N(µ,σ) = N(8;3) minutos
X < 4 minutos
X − µ 4 −8
z= = = −1,33
σ 3 4 8 X
-1,33 0 Z
Consultando
a tabela: P ( x ≤ 4) = P ( Z ≤ −1,33) = 0,5 − 0,4082 = 0,0918 = 9,18%

32. Distribuição Normal - Exemplos
ESTATÍSTICA NO CONTROLE DA PRODUÇÃO INDUSTRIAL
5) Um máquina produz peças com o diâmetro médio de 2,00” e o desvio-padrão
de 0,01”. As peças que se afastam da média por mais de 0,03” são consideradas
defeituosas. Qual é a percentagem de peças defeituosa?
f(x)
N(µ,σ) = N(2,00;0,01)
X1 = 2,03 e X2=1,97 µ =2
X − µ 2,03 − 2
z1 = = = +3
σ 0,01
X − µ 1,97 − 2
z2 = = = −3 1,97 2 2,03 X
σ 0,01 0
-3 3 Z
P ( x > 2,03)ouP ( x < 1,97) = P ( Z > 3) + P ( Z < −3)
Consultando
tabela: P ( Z > 3) + P ( Z < −3) = 0,0014 + 0,0014 = 0,28%

33. DÚVIDAS?
joao.alessandro@grupointegrado.br
jalmat@hotmail.com