Este documento apresenta um resumo sobre estatística e probabilidade. Ele discute conceitos como variáveis, amostragem, medidas de posição e dispersão, correlação, regressão, probabilidade, variáveis aleatórias e testes de hipóteses. O documento está organizado em 13 capítulos e fornece exemplos e exercícios para cada tópico discutido.

















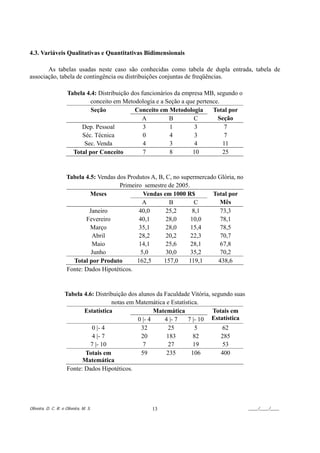















![7.3. Exercícios – Parte I – A1
1) Faça o gráfico de barras, o de composição em setores e o de Pareto para os dados fornecidos na
Tabela 7.7.
Tabela 7.7: Defeitos em elementos estruturais da porta
Tipo de Defeito Frequência Absoluta
Partes Salientes 5
Fora do Contorno 30
Partes mal aparadas 25
Total 60
2) Observe a sua conta de luz de 2007 e construa um gráfico temporal e um gráfico de barras,
colocando no eixo x, os meses (janeiro, ..., dezembro) e no eixo y, consumo de energia (em kWh).
3) Desenhe o ramo-e-folhas, box-plot e o dot plot para os dados das taxas médias geométricas de
incremento anual (por 100 habitantes) dos 30 maiores municípios do Brasil abaixo:
3,67 1,82 3,73 4,10 4,30
1,28 8,14 2,43 4,17 5,36
3,96 6,54 5,84 7,35 3,63
2,93 2,82 8,45 5,28 5,41
7,77 4,65 1,88 2,12 4,26
2,78 5,54 0,90 5,09 4,07
4) Construa uma tabela de classes de freqüências para os dados do exercício 3, com intervalos de
amplitude 1, de 0 a 10, isto é:
Taxas Freqüência Absoluta Proporção Densidade
[0, 1)
[1, 2)
[2, 3)
[3, 4)
[4, 5)
[5, 6)
[6, 7)
[7, 8)
[8, 9)
[9, 10]
em seguida, faça o histograma.
Oliveira, D. C. R. e Oliveira, M. S. 31 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-36-320.jpg)



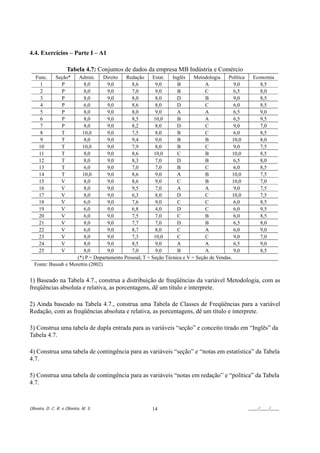
![8.3. Coeficiente de Correlação
O coeficiente de correlação linear é definido como:
n n
∑(X i − X )(Yi − Y ) ∑X Y i i − nXY
r= i =1
= i =1
(9.1)
(n − 1) S x S y (n − 1) S x S y
onde X e Y são as médias amostrais das variáveis X e Y , respectivamente.
S x e S y são os desvios padrão das variáveis X e Y , respectivamente
n n
∑(X i − X )2 ∑ (Y i − Y )2
Recordando: S x = i =1
e Sy = i =1
n −1 n −1
Propriedades do coeficiente de correlação linear
O valor do coeficiente de correlação linear situa no intervalo [-1, 1], ou seja,
−1 ≤ r ≤ 1
Classificação da correlação
1. r = 1 indica correlação linear positiva e perfeita;
2. r = −1 indica correlação linear negativa e perfeita;
3. r = 0 indica inexistência de correlação linear;
4. − 1 ≤ r ≤ 0 indica correlação linear negativa;
5. 0 ≤ r ≤ 1 indica correlação linear positiva.
Gráficos - Exemplos da classificação da correlação
r = 1 , correlação linear positiva e perfeita r = −1 , correlação linear negativa e perfeita
r ≅ 0 , inexistência de correlação linear
40
30
Y
20
10
10 20 30 40 50
Oliveira, D. C. R. e Oliveira, M. S. 35 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-40-320.jpg)














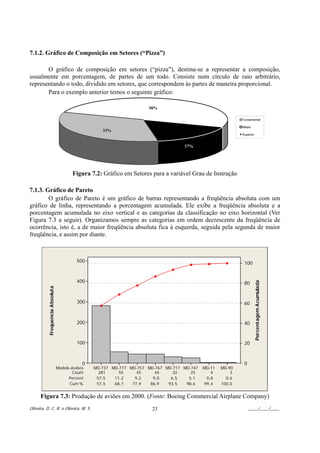
![9.8. Definição Subjetiva
Definição 7 (Subjetiva): Cada indivíduo, baseado em informações anteriores e na sua opinião
pessoal a respeito de um evento em questão, pode ter uma resposta para a probabilidade desse
evento.
Exemplo: Um médico experiente consegue calcular uma probabilidade do indivíduo ter uma
determinada doença baseado nos sintomas que o indivíduo apresenta.
9.9. Definição Moderna
Definição 8 (Moderna): Probabilidade é uma função P(.), que associa a cada evento do espaço
amostral Ω, um número real, pertencente ao intervalo [0, 1], satisfazendo os seguintes axiomas:
(1) 0 ≤ P(A) ≤ 1.
(2) P(Ω) = 1.
(3) Se A e B são eventos mutuamente exclusivos: P(A∪B) = P(A) + P(B).
Exemplos:
Segue alguns exemplos de funções já descobertas na literatura para calcular
probabilidades, que serão discutidas em detalhes nos capítulos posteriores.
1) Distribuição Bernoulli
P(X = x ) = p x (1 − p )1− x , x = 0, 1.
2) Distribuição Binomial
⎛n⎞
P(X = x ) = ⎜ ⎟p x (1 − p ) , x = 0, 1, ..., n.
n−x
⎜p⎟
⎝ ⎠
3) Distribuição Hipergeométrica
⎛ r ⎞⎛ N − r ⎞
⎜ ⎟⎜
⎜ x ⎟⎜ n − x ⎟
⎟
⎝ ⎠⎝ ⎠ , 0 ≤ x ≤ mínimo(r, n).
P(X = x ) =
⎛ N⎞
⎜ ⎟
⎜n⎟
⎝ ⎠
4) Distribuição Poisson
e − λ λx
P(X = x ) = , x = 0, 1, ...
x!
5) Distribuição Normal
1
1 −
2
(x −µ ) 2
f (x) = e 2σ , - ∞ < x< + ∞
σ 2π
Oliveira, D. C. R. e Oliveira, M. S. 51 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-56-320.jpg)
![6) Distribuição t de Student
−(k +1) / 2
Γ[(k + 1) / 2] ⎛ x 2
⎜1 +
⎞
⎟
f (x) = , - ∞ < x< + ∞
Γ[k / 2] πk ⎜ ⎝ k ⎟
⎠
7) Distribuição Qui-Quadrado
k
−1 − x
1 2
f (x) = x e 2,x>0
k
[
Γ k/2 22 ]
Propriedades
P1: P(∅) = 0, onde ∅ é o conjunto vazio.
P2: Se Ac for o evento complementar de A, então P(Ac) = 1 – P(A).
P3: Se A e B forem dois eventos quaisquer, então P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
P4: Se A ⊂ B, então P(A) ≤ P(B).
Nos capítulos posteriores veremos algumas distribuições de probabilidade para
variáveis discretas e contínuas comumente utilizadas.
9.10. Probabilidade Condicional
A probabilidade condicional surge, por exemplo, quando se deseja calcular a probabilidade
de um evento A ocorrer sabendo que um evento B já ocorreu.
Sejam A e B dois eventos associados a um mesmo espaço amostral Ω. Denota-se por
P(A|B) a probabilidade condicionada do evento A, quando o evento B tiver ocorrido.
Sempre que calculamos P(A|B), estamos essencialmente calculando P(A) em relação ao
espaço amostral reduzido devido a B ter ocorrido, em lugar de fazê-lo em relação ao espaço
amostral original Ω.
Assim, uma definição mais formal de probabilidade condicional é dada pela definição 9.
Definição 9 (Probabilidade Condicional): Dados dois eventos A e B, a probabilidade condicional
de A dado que ocorreu B é representada por P(A | B) e definida por
P( A ∩ B)
P( A | B) = , P( B) > 0
P ( B)
Da definição de probabilidade condicional, obtemos a regra do produto de probabilidades.
P( A ∩ B) = P( B)P( A | B)
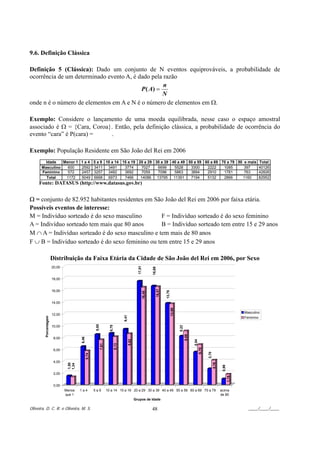
Exemplo: Voltando ao Exemplo da População Residente em São João del Rei em 2006, temos:
Idade Menor 1 1a4 5 a 9 10 a 14 15 a 19 20 a 29 30 a 39 40 a 49 50 a 59 60 a 69 70 a 79 80 e mais Total
Masculino 600 2592 3411 3491 3774 7027 6699 5528 3300 2222 1085 397 40126
Feminino 572 2457 3257 3482 3692 7059 7096 5863 3894 2910 1781 763 42826
Total 1172 5049 6668 6973 7466 14086 13795 11391 7194 5132 2866 1160 82952
Fonte: DATASUS (http://www.datasus.gov.br)
Oliveira, D. C. R. e Oliveira, M. S. 52 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-57-320.jpg)





![Solução: Calculemos inicialmente E(X), que é o número esperado de aparelhos vendidos em uma
semana:
E(X) = (0)(0,1) + (1)(0,1) + (2)(0,2) + (3)(0,3) + (4)(0,2) + (5)(0,1) = 2,70.
Para x unidades vendidas o lucro é 20x. Logo, o lucro esperado é de R$ 54,00.
10.3. Variância
Assim como a média é uma medida de posição de uma v.a., é natural que procuremos uma
medida de dispersão dessa variável em relação à média. Essa medida é a variância, a ser
representada por σ2 e definida por
n
σ 2 = Var (X) = ∑ ( x i − E (X)) 2 P(X = x i )
i =1
Desenvolvendo o termo quadrático do somatório, obtemos uma expressão mais fácil de calcular a
variância dada por:
σ 2 = Var (X) = E(X 2 ) − [E (X)]2
n
onde E(X 2 ) = ∑ x i2 P(X = x i ) .
i =1
Desvio Padrão
O desvio padrão (σ) é a raiz quadrada positiva da variância. Tem sobre essa última a
vantagem de exprimir a dispersão na mesma unidade de medida da v.a.:
σ = σ2
10.4. Exercício – Parte II – A2
1) A distribuição de X: nº de crianças por domicílio numa determinada região é dada pela tabela
abaixo:
X 0 1 2 3 4 5
P(X = x) 0,10 0,15 0,25 0,30 0,15 0,05
Calcule:
(a) O número médio de crianças por domicílio, µX.
(b) O desvio padrão de X, σX.
(c) A probabilidade P{µX - σX ≤ X ≤ µX + σX}.
10.5. Distribuição Bernoulli
Na prática existem muitos experimentos que admitem apenas dois resultados.
Exemplos:
1) Uma peça é classificada como boa ou defeituosa;
2) Um entrevistado concorda ou não com a afirmação feita;
3) O resultado de um exame médico para detecção de uma doença é positivo ou negativo;
4) No lançamento de um dado ocorre ou não a face 5.
Oliveira, D. C. R. e Oliveira, M. S. 58 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-63-320.jpg)







![Exemplo: Para uma variável que têm densidade f(x) = 2x, 0<x<1, então:
1 1
2 31 2
E (X) = ∫ x 2 x dx = ∫ 2x 2 dx = x 0=
0 0
3 3
Definição: A variância de uma variável aleatória contínua é definida por:
∞
Var(X) = E(X2) – [E(X)]2, onde E(X2) = ∫x
2
f ( x ) dx
−∞
Exemplo: Para uma variável que têm densidade f(x) = 2x, 0<x<1, então:
2 1 1
E(X) = 2 41 2
3 E (X 2 ) = ∫ x 2 2x dx = ∫ 2 x 3 dx = x 0=
0 0
4 4
Logo, Var(X) = 2/4 – (2/3)2 =1/18 = 0,056
Também podemos obter o Desvio Padrão: 0,056 ≅ 0,23
Exercícios – Parte II – A2:
1) O diâmetro de um cabo elétrico é uma variável aleatória com fdp dada por:
f(x) = 6x(1-x) para 0 < x < 1 e f(x) = 0 fora desse intervalo. Qual a probabilidade do diâmetro ser:
(a) Igual a 0,5 cm?
(b) Entre 0,10 e 0,20?
(c) Maior que 0,5?
(d) Menor que 1?
2) A quantia gasta anualmente, em milhões de reais, na manutenção do asfalto de uma cidade do
interior é representada pela variável y modelada pela função:
f(y) = (8/9)y – (4/9), se 0,5 ≤ y ≤ 2 e
f(y) = 0, caso contrário.
Qual a probabilidade da quantia gasta ser inferior a 0,8 milhões de reais?
3) O tempo de sobrevivência de uma bateria (em anos) pode ser modelado pela função:
f(x) = e-x, se x ≥ 0 e f(x) = 0, caso contrário.
(a) Qual a probabilidade da bateria sobreviver mais que 2 anos?
(b) Qual é o tempo médio de sobrevivência da bateria?
4) O diâmetro de um cabo elétrico é uma v. a. com fdp dada por: f(x) = 6x(1-x) para 0 < x < 1 e
f(x) = 0 fora desse intervalo.
(a) Verifique se f(x) é uma fdp, através do item (b) da definição 2.
(b) Obtenha a F(x).
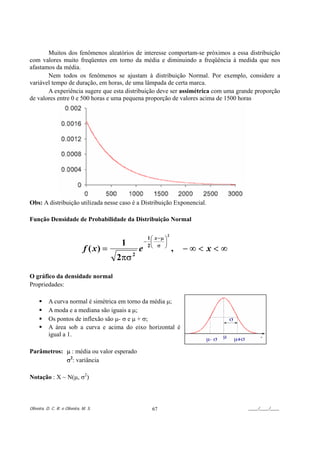
11.2. Distribuição Normal
A distribuição Normal é uma das mais importantes distribuições contínuas de
probabilidade. Foi introduzida em 1730 por D´Moivre e depois foi muito utilizada em Astronomia
pelo alemão físico/matemático Gauss, trazendo muita confusão para várias pessoas que por esse
motivo, acham que foi Gauss que a descobriu.
Oliveira, D. C. R. e Oliveira, M. S. 66 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-71-320.jpg)


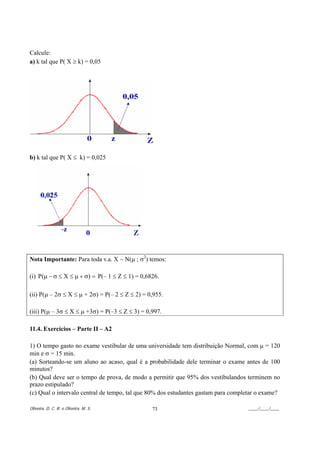




![Exemplo: Sejam, p: proporção de alunos da UFSJ que foram ao cinema pelo menos uma vez no
último mês, e X: número de estudantes que respondem “sim” em uma pesquisa com n
entrevistados. Suponha que foram entrevistados n = 500 estudantes e que, desses, x = 100 teriam
afirmado que foram ao cinema pelo menos uma vez no último mês. A estimativa pontual
(proporção amostral) é dada por: p = ( x / n ) = (100 / 500 ) = 0 , 20 , ou seja, 20% dos estudantes
ˆ
entrevistados afirmaram que foram ao cinema pelo menos uma vez no último mês.
Note que, outra amostra de mesmo tamanho pode levar a uma outra estimativa pontual para
p.
Estimativa Intervalar
Idéia: Se selecionarmos várias amostras de uma população contendo n dados, observaremos que
cada amostra terá sua respectiva proporção. A fim de obtermos uma estimativa da proporção da
população em estudo com certo grau de confiabilidade, recorremos a um intervalo de confiança,
que delimita essa proporção.
A estimativa por intervalo de p corresponde a um intervalo determinado da seguinte
maneira:
[p − ε
ˆ ; p + ε ],
ˆ
sendo que ε representa o erro amostral ou margem de erro.
Na prática o intervalo de confiança com um coeficiente de confiança γ é dado por:
⎡ p (1 − p )
ˆ ˆ p (1 − p ) ⎤
ˆ ˆ
IC (p,γ) = ⎢ p − z
ˆ ;p+z
ˆ ⎥
⎣ n n ⎦
p (1 − p )
ˆ ˆ
Note que, ε = z . O valor de z é obtido da distribuição normal padrão. Assim, os valores
n
de z que limitam os níveis de confiança, onde z é tal que γ = P(-z ≤ Z ≤ z) na N (0,1) são:
γ 90% 95% 99%
z
Exemplos
1) No exemplo da UFSJ, considere agora, n = 500 e p = 0,20 . Construa um intervalo de confiança
ˆ
para p com coeficiente de confiança γ = 0,95.
Resolução: Como γ = 0,95 fornece z = 1,96, o intervalo é dado por:
⎡ p (1 − p )
ˆ ˆ p (1 − p ) ⎤ ⎡
ˆ ˆ 0,20 x0,80 0,20 x0,80 ⎤
⎢p − z
ˆ ;p+z
ˆ ⎥ = ⎢0,20 − 1,96 ; 0,20 + 1,96 ⎥ = [0,165; 0,235]
⎣ n n ⎦ ⎣ 500 500 ⎦
Nesse intervalo (γ=0,95), a estimativa pontual para p é 0,20, com um erro amostral ε igual a
0,035.
Interpretação do IC com γ = 95%: Se sortearmos 100 amostras de tamanho n = 500 e
construirmos os respectivos 100 intervalos de confiança, com coeficiente de confiança de 95%,
esperamos que, aproximadamente, 95 destes intervalos contenham o verdadeiro valor de p.
Oliveira, D. C. R. e Oliveira, M. S. 78 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-83-320.jpg)

![Obtemos, então, uma amostra aleatória de tamanho n de X, que representamos por X1, X2, ..., Xn.
Uma estimador pontual para µ é dado pela média amostral,
X1 + X 2 + K + X n n
Xi
X=
n
= ∑
i =1 n
Estimativa Intervalar
Se selecionarmos várias amostras de uma população contendo n dados, observaremos que cada
amostra terá sua respectiva média. A fim de obtermos uma estimativa da média da população em
estudo com certo grau de confiabilidade, recorremos a um intervalo de confiança, que delimita essa
média.
Uma estimador intervalar ou intervalo de confiança para µ tem a forma:
[X − ε ; X + ε ]
sendo ε o erro amostral (margem de erro).
Teorema Central do Limite
Se X1, ..., Xn representa uma amostra aleatória de uma variável X de média µ e desvio padrão σ,
então para n grande
⎛ σ2 ⎞
X ~ N ⎜ µ,
⎜ ⎟
⎟
⎝ n ⎠
Portanto, para n grande a média amostral tem distribuição Normal de média µ e desvio padrão
σ/ n .
Na prática, temos que o intervalo de confiança para µ com um nível de confiança γ é dado
por:
⎡ σ σ ⎤
⎢x − z n ; x + z n ⎥
⎣ ⎦
onde x é a média amostral, σ é o desvio padrão populacional e n é o tamanho amostral. Sendo
σ
assim, temos que o erro é: ε = z .
n
Exemplo: Não se conhece o consumo médio de combustível de automóveis da marca T. Sabe-se,
no entanto, que o desvio padrão do consumo de combustível de automóveis dessa marca é 10 km/l.
Na análise de 100 automóveis da marca T, obteve-se consumo médio de combustível de 8 km/l.
Encontre um intervalo de confiança para o consumo médio de combustível dessa marca de carro.
Adote um nível de confiança igual a 95%.
X: Consumo de combustível da marca T;
σ = 10 km/l n = 100 ⇒ x = 8 km/l
γ = 0,95 ⇒ z=1,96
⎡ σ σ ⎤ ⎡ 10 10 ⎤
⎢X − z ;X + z ⎥ = ⎢8 − 1,96 ;8 + 1,96 ⎥ = [8 − 1,96 ;8 + 1,96 ] = [6,04 ;9,96 ]
⎣ n n⎦ ⎣ 100 100 ⎦
Portanto, a estimativa intervalar de 95% de confiança é [6,04 ;9,96 ] .
Oliveira, D. C. R. e Oliveira, M. S. 80 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-85-320.jpg)
![Exemplo: Deseja-se estimar o tempo médio de estudo (em anos) da população adulta de um
município. Sabe-se que o tempo de estudo tem distribuição normal com desvio padrão σ = 2,6
anos. Foram entrevistados n = 25 indivíduos, obtendo-se para essa amostra, um tempo médio de
estudo igual há 10,5 anos. Obter um intervalo de 90% de confiança para o tempo médio de estudo
populacional.
X: tempo de estudo, em anos X ~ N(µ, 2,62)
n = 25 ⇒ x = 10,5 anos γ = 0,90⇒ z=1,65
A estimativa intervalar com 90% de confiança é dada por:
⎡ σ σ ⎤ ⎡ 2 ,6 2 ,6 ⎤
⎢X − z ;X + z ⎥ = ⎢10 ,5 − 1,65 ;10 ,5 + 1,65 ⎥ = [9 ,64 ;11,36 ]
⎣ n n⎦ ⎣ 25 25 ⎦
12.5. Exercícios – Parte III – A3
1) Estabeleça um intervalo de confiança para a média populacional, sendo que o desvio padrão
populacional é 4, o tamanho amostral é n = 36 e a média amostral igual a 30. Utilize um nível de
confiança de 95% para a média.
2) Uma amostra de n = 64 elementos de uma variável normalmente distribuída forneceu média
25,4, sendo que o desvio padrão populacional é 5,2. Determine o intervalo de confiança de 90%
para a média.
12.6. Estimativa para Média Populacional com Variância Desconhecida
Na prática, a variância populacional σ2 é desconhecida e é substituída por sua estimativa:
1 n
S2 = ∑ ( X i − X )2
( n − 1) i =1
Lembrar que a estimativa amostral do desvio padrão σ é s = s2
Oliveira, D. C. R. e Oliveira, M. S. 81 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-86-320.jpg)

![porém para amostras menores que esse valor essa variável vai se afastando de z e, quanto menor
for o valor de n, maior é o afastamento existente entre a variável t e z.
A tabela que fornece os valores de t, contém na 1a. linha, a área locada nas caudas da curva,
à esquerda de –t e à direita de t. Na 1a. coluna, está os graus de liberdade (n-1). Na interseção dos
valores considerados, temos os valores de t correspondente.
Exemplo: Qual o intervalo de confiança para a média, no nível de 95%, sendo que uma amostra de
tamanho 20 forneceu média 38 e desvio padrão 5?
Solução:
x = 38 , n = 20, s = 5. No nível de 95%, obtemos o valor de t cruzando na tabela da t – Student: p =
5% e gl = n-1 = 20-1 = 19 → t = 2,093. Assim:
⎡ s s ⎤ ⎡ 5 5 ⎤
IC[µ, 95%] = ⎢ x − t , x+t ⎥ = ⎢38 − 2,093 , 38 + 2,093 ⎥ = [35.66 , 40.34]
⎣ n n⎦ ⎣ 20 20 ⎦
Exemplo: Estabeleça limites de confiança para a média, no nível de 90%, sendo que uma amostra
de tamanho 16 forneceu média 70 e desvio padrão 6,8?
Solução:
Temos que x = 70 , n = 16, s = 6,8 e para um nível de 90%, obtemos o valor de t cruzando na
tabela da t – Student: p = 10% e gl = n-1 = 16-1 = 15 → t = 1,753. Assim:
⎡ s s ⎤ ⎡ 6,8 6,8 ⎤
IC[ µ , 90%] = ⎢ x − t , x +t ⎥ = ⎢70 − 1,753 , 70 + 1,753 ⎥ = [ 67.02 , 72.98]
⎣ n n⎦ ⎣ 16 16 ⎦
12.7. Exercício – Parte III – A3
Determine o intervalo de confiança de 99% para a média, sendo que uma amostra de
tamanho n = 9 forneceu média 75 e desvio padrão 7.
Oliveira, D. C. R. e Oliveira, M. S. 83 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-88-320.jpg)












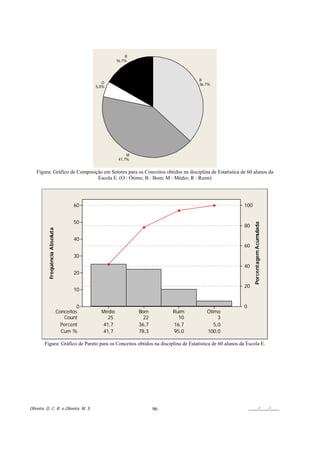
![6) (a) mínimo = 10; máximo = 22; média = 16,913; moda = 14.1, 16, 16.9, 19.5, 22; mediana = 16,9; Q1 = 15,0; Q3 = 19,5.
(b) amplitude = 12; variância = 8,296; desvio-padrão = 2,88; intervalo-interquartil = 4,5.
(c)
Tabela: Comprimento de 31 canos PVC vendidos em uma loja de material de construção
Comprimento Freqüência Absoluta Proporção Porcentagem Densidade
[10, 12) 1 0,0322581 3,2 0,0161290
[12, 14) 3 0,0967742 9,7 0,0483871
[14, 16) 6 0,1935480 19,4 0,0967742
[16, 18) 10 0,3225810 32,2 0,1612900
[18, 20) 6 0, 1935480 19,4 0,0967742
[20, 22] 5 0,1612907 16,1 0,0806452
Total 31 1 100 ------
Interpretação: A maior parte dos canos tem comprimento entre 16 e 18m (32,2%), ....(descrever a coluna da
porcentagem)
(d)
0,18
0,16129
0,16
0,14
0,12
Densidade
0,0967742 0,0967742
0,10
0,0806452
0,08
0,06
0,0483871
0,04
0,016129
0,02
0,00
10 12 14 16 18 20 22
Comprimento
Figura: Histograma do comprimento de 31 canos PVC vendidos em uma loja de material de construção.
(e)
10 11 12 13 14 15 16 17 18 19 20 21 22
Compriment o
Figura: Diagrama de dispersão unidimensional do comprimento de 31 canos PVC vendidos em uma loja de material de
construção.
Oliveira, D. C. R. e Oliveira, M. S. 97 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-102-320.jpg)


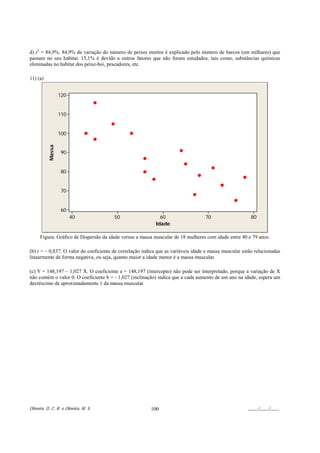
![APÊNDICE B
Gabarito da Lista de Exercícios 2
1) (a) (A ∪ B) b) (A ∩ Bc) ∪ (Ac ∩ B) c) (A ∪ B)c d) (A ∩ Bc)
2) a) P(A∪B) ≅ 0,0358 b) P((A ∪ B)c) ≅ 0,9641 c) P((A ∩ Bc)) ≅ 0,023
3) P(M|A) = 0,292
4)
X 15 17 18 20 E[X] =
P(X) 0,3575 0,1925 0,2925 0,1575 17,05
5) 0,8192
6) (a) 0,59049 (b) 0,32805 (c) 0,99144
7) (a) 0,5 (b) 0,33333
8) (a) 0,376812 (b) 0,282609 (c) 0,0376812 (d) 0,0086957
9) (a) 0,367879 (b) 0,981011 (c) 0,264242
10) (a) 0,0000454(b) 0,0103361 (c) ≅ 0
11) (a) 0,4332 (b) 0,0668 (c) 0,0062 (d) ≅ 41,34
12) (a) 0,2967 (b) 0,0062 (c) 0,0475
13) (a) boas: 0,8904 recuperáveis: 0,0932 defeituosas: 0,0164 (b) E[T] ≅ 0,09
Oliveira, D. C. R. e Oliveira, M. S. 101 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-106-320.jpg)
![APÊNDICE C
Gabarito da Lista de Exercícios 3
⎡ 0,03.0,97 0,03.0,97 ⎤
1) IC[P ; 95%] = ⎢0,03 − 1,96 ; 0,03 + 1,96 ⎥ = [0 ; 0,0634]
⎣ 100 100 ⎦
⎡ 0,16.0,84 0,16.0,84 ⎤
2) IC[P ; 90%] = ⎢0,16 − 1,645 ; 0,16 + 1,645 ⎥ = [0,075 ; 0,245]
⎣ 50 50 ⎦
⎡ 5,2 5,2 ⎤
3) IC[µ ; 90%] = ⎢25,4 − 1,645 ; 25,4 + 1,645 ⎥ = [24.3 ; 26.5]
⎣ 64 64 ⎦
⎡ 7 7 ⎤
4) IC[µ ; 99%] = ⎢75 − 3,355 ; 75 + 3,355 ⎥ = [67.2 ; 82.8]
⎣ 9 9⎦
5) Hipóteses: Ho: p = 0,5
Ha: p ≠ 0,5
Nível de Significância: α = 0,10
Proporção Amostral: p = 0,42
ˆ
0,42 − 0,5
Estatística do Teste: z observado = = −1.6
0,5.0,5
100
Regra de Decisão: Pela tabela da distribuição normal, Ha e nível de significância:
RC = (-∞ , -1.645] ∪ [1.645 , +∞)
RA = (-1.645 , 1.645)
Conclusão: Como zobservado ∈ RA, então não rejeito Ho com um nível de significância de 10%, ou seja, não podemos
afirmar que a moeda é viciada.
6) Hipóteses: Ho: p = 0,05
Ha: p ≠ 0,05
Nível de Significância: α = 0,10
Proporção Amostral: p = 0,06
ˆ
0,06 − 0,05
Estatística do Teste: z observado = ≅ 0.32
0,05.0,95
50
Regra de Decisão: Pela tabela da distribuição normal, Ha e nível de significância:
RC = (-∞ , -1.645] ∪ [1.645 , +∞)
RA = (-1.645 , 1.645)
Conclusão: Como zobservado ∈ RA, então não rejeito Ho com um nível de significância de 10%, ou seja, podemos
afirmar que 5% dos alunos dessa escola de 1º grau são canhotos.
7) Hipóteses: Ho: µ = 8 kg
Ha: µ < 8 kg
Nível de Significância: α = 0,05
Oliveira, D. C. R. e Oliveira, M. S. 102 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-107-320.jpg)
![7,2 − 8
Estatística do Teste: z observado = = −2
2
25
Regra de Decisão: Pela tabela da distribuição normal, Ha e nível de significância:
RC = (-∞ , -1.645]
RA = (-1.645 , +∞)
Conclusão: Como zobservado ∈ RC, então rejeito Ho com um nível de significância de 5%, ou seja, a média de
consumo per capita é menor que 8 kg.
8) Hipóteses: Ho: µ = 300
Ha: µ < 300
Nível de Significância: α = 0,10
290 − 300
Estatística do Teste: t observado = = −5
6
9
Regra de Decisão: Pela tabela da t de Student com Graus de Liberdade = 8 e p = 20%, Ha e nível de significância:
RC = (-∞ , -1.397]
RA = (-1.397 , +∞)
Conclusão: Como zobservado ∈ RC, então rejeito Ho com um nível de significância de 10%, ou seja, a vida média de
B é menor que a de A.
9) Hipóteses: Ho: µ = 175
Ha: µ ≠ 175
Nível de Significância: α = 0,10
173 − 175
Estatística do Teste: t observado = = −0,5
16
16
Regra de Decisão: Pela tabela da t de Student com Graus de Liberdade = 15 e p = 10%, Ha e nível de significância:
RC = (-∞ , -1.753] ∪ [1.753 , +∞)
RA = (-1.753 , 1.753)
Conclusão: Como zobservado ∈ RA, então não rejeito Ho com um nível de significância de 10%, ou seja, podemos
afirmar que a altura média é de 175 cm.
Oliveira, D. C. R. e Oliveira, M. S. 103 ____/____/____](https://image.slidesharecdn.com/apostilaestatistica2009mec-111211190203-phpapp02/85/Apostila-estatistica-2009-mec-108-320.jpg)
