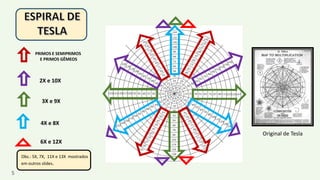
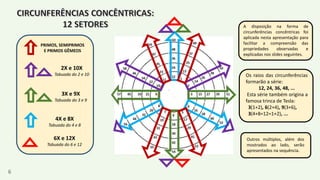
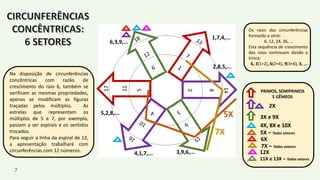
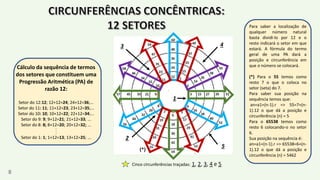
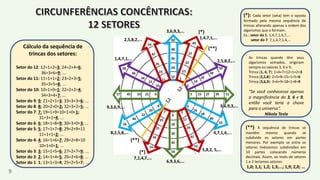
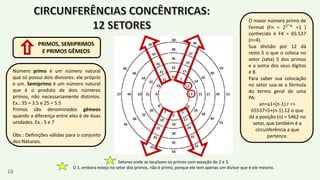
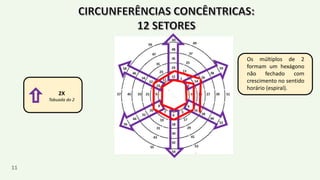
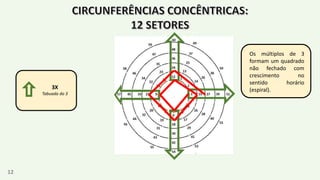
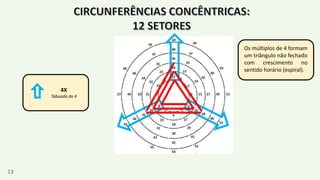
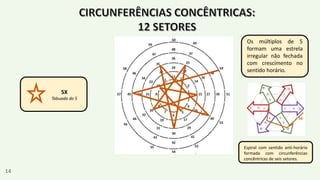
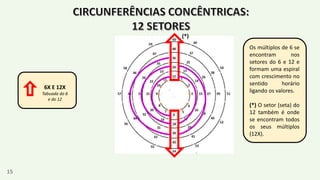
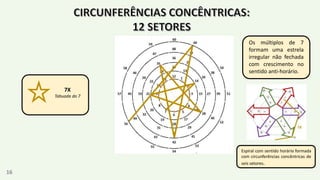
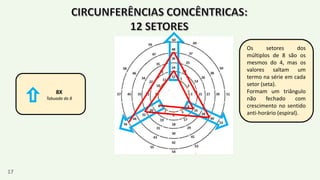
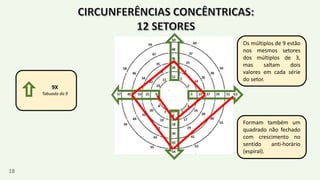
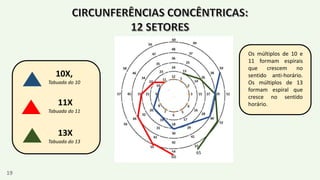
O documento apresenta um resumo biográfico de Nikola Tesla, destacando sua contribuição à eletricidade e suas invenções, como a corrente alternada. Ele também introduz a 'espiral de Tesla', um conceito relacionado à teoria dos números que revela padrões nas distribuições numéricas e suas propriedades. Além disso, o autor sugere que a espiral pode ter aplicações em diversas áreas e convida a um estudo mais aprofundado sobre o tema.