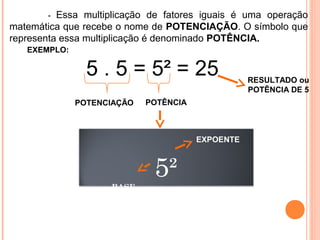
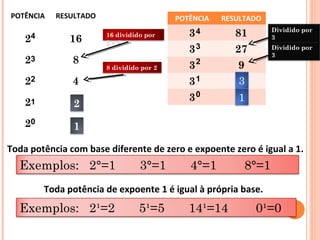
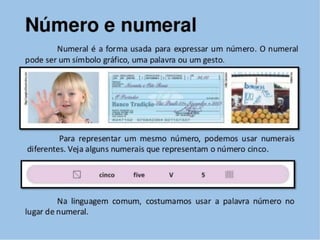
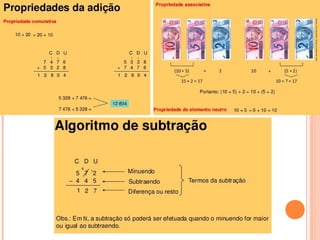
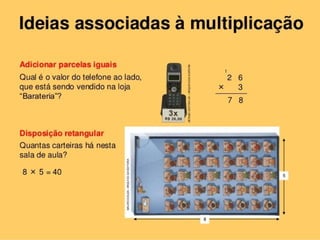
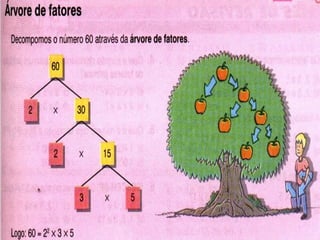
1) O documento discute conceitos básicos de matemática como números naturais, inteiros, racionais e operações entre eles. 2) Inclui exemplos de adição, subtração, multiplicação e divisão de números inteiros e racionais. 3) Explica a decomposição de números em seus fatores primos e a representação de frações como decimais.

1. MATEMÁTICA – ENSINO FUNDAMENTALMATEMÁTICA – ENSINO FUNDAMENTAL
AULA 1AULA 1

2. Os números são utilizados para representar
quantidades, códigos, medidas, ordem ou posição.

7. OPERAÇÕES COM NÚMEROS NATURAIS

16. O Conjunto dos Números Inteiros, que representamos
pela letra Z.
A letra Z corresponde à letra inicial da palavra
alemã Zahl, que quer dizer “número”.
O conjunto dos números inteiros (Z) é a união dos números
naturais (N) com os números negativos.
N = {0 , 1, 2, 3, 4, 5, 6, ...}
números negativos: ..., - 4, - 3, - 2, - 1
Z = {..., - 4, - 3, -2, - 1, 0, 1, 2, 3, 4, 5, 6, 7, ...}
Observação:
Na verdade o zero não é um número natural, pois ele, por si só, não serve
para contar, que é a principal função dos números naturais. Porém, optamos
por mantê-lo no conjunto N.

17. REPRESENTAÇÃO E COMPARAÇÃO DE NÚMEROSREPRESENTAÇÃO E COMPARAÇÃO DE NÚMEROS
INTEIROSINTEIROSVamos observar a reta numérica abaixo:
Agora, vamos responder:
a)Quem é maior 2 ou 3? b) Quem é maior -2 ou – 3?
c) Quem é maior -4 ou 1?
Veja a representação geométrica dos números inteiros
na reta abaixo:
NÚMEROS OPOSTOS OU SIMÉTRICOS
0 + 1 + 2 + 3 + 4- 1- 2- 3- 4

18. OPERAÇÕES COM NÚMEROS INTEIROS
Tanto no conjunto dos números naturais como no conjunto dos
números inteiros, temos 6 operações:
 Adição e Subtração;
 Multiplicação e Divisão;
 Potenciação e Radiciação.
Adição e subtração de números inteiros
Quando os sinais dos números são iguais, devemos adicionar
mantendo o sinal dos números.
+ 9 + 9 = + 18 –1 – 1 = – 2
+ 4 + 6 = +10 –7 – 8 = – 15

19. Quando os sinais são diferentes, devemos subtrair os números
mantendo o sinal do número de maior módulo.
– 4 + 6 = + 2 – 10 + 5 = – 5 – 20 + 36 = + 16
– 60 + 80 = + 20 – 21 + 5 = – 16 – 91 + 10 = – 81
Caso ocorra a presença de parênteses nas operações entre os
números inteiros, devemos eliminá-los, utilizando o jogo do sinal.
(–8) + (–2) + (–7) (+81) + (–12) – (+ 7)
– 8 – 2 – 7 = - 17 + 81 – 12 – 7
+ 81 – 19 = + 62
Resolver as operações indicadas nos parênteses, nos colchetes e
nas chaves, e logo em seguida, realizar o jogo de sinal.
(+ 8 + 9) – (+ 5 – 6) – (9 + 1)
+17 – (– 1) – (+ 10)
+17 + 1 – 10
+ 18 – 10 = + 8

20. –[–(2 + 4) – (– 4 –13)]
–[– (6) – (– 17)]
–[– 6 + 17]
– [11] = – 11
–{–[(2 + 3) – (7 – 8) + (–6 –4)]}
–{–[(5) – (–1) + (–10)]}
–{–[5 + 1 – 10]}
–{–[–4]} = – 4
Ao eliminar parênteses, utilize o seguinte quadro de sinais:
+ ( + ) = +
+ ( – ) = –
– ( + ) = –
– ( – ) = +
Multiplicação e Divisão de números inteiros

23. 3 . 3 = 3²
3 é o número BASE dessa
multiplicação, e o 2, a
quantidade de fatores que ela
nos EXPÕE.
2 . 2 . 2 . 2 . 2 = 2
O número 2 é a BASE dessa multiplicação, e o número
5 é a quantidade de fatores EXPOSTO por essa
operação
10.10.10.10= 10
10 é a BASE e 4, o EXPOENTE.
5
4
Potenciação de números inteiros
7.7.7 = 7³
5.5.5.5 = 5
12.12.12.12.12 = 12 5
MAIS EXEMPLOS:
1.1.1.1.1.1 = 14 6

24. - Essa multiplicação de fatores iguais é uma operação
matemática que recebe o nome de POTENCIAÇÃO. O símbolo que
representa essa multiplicação é denominado POTÊNCIA.
5²
BASE
EXEMPLO:
5 . 5 = 5² = 25
POTENCIAÇÃO
RESULTADO ou
POTÊNCIA DE 5
POTÊNCIA
EXPOENTE

25. POTÊNCIA RESULTADO
2 16
2 8
2 4
2 ?
2 ?
4
3
2
1
0
POTÊNCIA RESULTADO
3 81
3 27
3 9
3 ?
3 ?
4
3
2
1
0
16 dividido por
2 = 8
8 dividido por 2
= 4
2
1
Dividido por
3
Dividido por
3
3
1
Toda potência com base diferente de zero e expoente zero é igual a 1.
Exemplos: 2°=1 3°=1 4°=1 8°=1
Toda potência de expoente 1 é igual à própria base.
Exemplos: 2¹=2 5¹=5 14¹=14 0¹=0

26. Radiciação de números inteiros

28. SÍMBOLOS: Possui apenas 10 símbolos;
BASE: Base dez, ou seja: agrupamentos
de dez em dez;
POSICIONAL: O mesmo símbolo
representa valores diferentes
dependendo da posição que ocupa no
numeral;
ZERO: indica uma posição vazia ou uma
casa vazia.
Sistema de Numeração Decimal
Características do Sistema de Numeração Decimal

29. ADITIVOADITIVO: O valor do número é obtido pela adição dos valores posicionais
que os símbolos adquirem nos respectivos lugares que ocupam.
400425
MULTIPLICATIVOMULTIPLICATIVO: Um algarismo escrito a esquerda de outro vale dez
vezes o valor posicional que teria se estivesse ocupando a posição do
outro; ex: 333=3X100+3X10+3
3 X100333

30. Um pouco de HistóriaUm pouco de HistóriaUm pouco de HistóriaUm pouco de História
•Não existem só números inteiros {1,2,3,4 ... }
•Entre o 1 e o 2 existem vários valores: (1,1 / 1,2 / 1,3 / 1,4 / 1,5 /
1,6 / 1,7 / 1,8 / 1,9)
•Se olharmos na régua, entre os valores inteiros, veremos alguns
valores intermédiários?
•Eles são chamados de números decimais!
Exemplos de números decimaisExemplos de números decimaisExemplos de números decimaisExemplos de números decimais
4,9 9,9 0,1 3,3 0,5

31. Leitura de números decimaisLeitura de números decimaisLeitura de números decimaisLeitura de números decimais
No sistema de numeração decimal, cada algarismo, da parte inteira ou decimal, ocupa
uma posição ou ordem, com as seguintes denominações:
Centenas Dezenas Unidades Décimos Centésimos Milésimos
Décimos
milésimos
Centésimos
milésimos
Milionésimos
Partes inteiras Partes decimais
Lemos a parte inteira, seguida da parte decimal, acompanhada das palavras:
•décimos ........................................... : quando houver uma casa decimal;
•centésimos....................................... : quando houver duas casas decimais;
•milésimos......................................... : quando houver três casas decimais;
•décimos milésimos .......................... : quando houver quatro casas decimais;
•centésimos milésimos ..................... : quando houver cinco casas decimais.
ExemplosExemplosExemplosExemplos
Centenas Dezenas Unidades Décimos Centésimos Milésimos
Décimos
milésimos
Centésimos
milésimos
Milionésimos
1, 6 5
1, 5
Partes inteiras Partes decimais
Daí, teremos:
1,65 = um inteiro e sessenta e cinco centésimos
1,5 = um inteiro e cinco décimos

32. Transformando em uma fração decimal.
0,8 =
8
10
0,35 = 35
100
2,125 = 2125
1000

34. DECOMPOSIÇÃO DE UM NÚMERO EM FATORESDECOMPOSIÇÃO DE UM NÚMERO EM FATORES
PRIMOSPRIMOS Todo número natural composto pode ser decomposto num
produto de dois ou mais fatores primos.
 Decomposição é o mesmo que fatoração.
Método prático de fatorarMétodo prático de fatorar……
15
5
60 2
30 2
5
3
1
Então:
60 = 2x2x3x5
125 5
25 5
5 5
1 Então:
125 = 5x5x5

36. NÚMEROS RACIONAISNÚMEROS RACIONAIS
O QUE SÃO?O QUE SÃO?
O conjunto dos números racionais é formado por todos
os quocientes de números inteiros a e b, em que b é não
nulo. O uso da letra "Q" é derivado da palavra latina
quotiē(n)s, cujo significado é quantas vezes .
N = conjunto dos
números naturais
Z = conjunto dos
números inteiros
Q = conjunto dos
números racionais

37. Você já ouviu dizer que toda fração é uma divisão? Pois então, se temos uma fração do
tipo ½ , nós podemos representá-la como 0,5, já que, ao dividirmos o numerador 1 pelo
denominador 2, obtemos o quociente 0,5. Portanto, podemos afirmar que os decimais e
as frações são alternativas para representar um mesmo número racional.
Exemplos de números inteiros expressos como decimais:
3 = 0,75 12 = 2,4 – 16 = – 8
4 5 2
EXEMPLOS DE NÚMEROS RACIONAISEXEMPLOS DE NÚMEROS RACIONAIS
Números Inteiros
Números Decimais Exatos
Números Decimais com infinitas ordens decimais (dízimas periódicas)